Numerical analysis of cast partials using the finite element method

1. Introduction

Many centers in the country and abroad are engaged in mathematical modeling of dental prostheses (including implants). One of them is the leading Institute of Dentistry, Medical University of Warsaw. Conducted their research work mostly limited to static systems analyzing biomechanical prostheses. Therefore, this type of issues dealt with Institute of Electronic Systems Military Technical Academy. It made an analysis of the mathematical evaluation dentures, both in extortion static and kinematic [1, 2]. This model takes also into account the gingival soft tissue.

Mathematical models of dental prostheses are very powerful and informative tool. They allow observation of strain and stress of each area dentures, with a variety of external excitations [3]. This makes it possible to evaluate the durability of the prosthesis, even in case of prolonged use.

Extending the scope for extortion kinematic modeling and modeling of passive pressure gingival soft tissue, will enable the development of a virtual prosthesis. In this way, it is possible to quickly carry out a modification of the prosthesis and adapt it to the specific condition of the teeth. This will allow the testing of such implants.

Typically, during the grinding feed effective load on each tooth is in the range 40-120 cycles/min [4, 5]. Then the static load effective pressure on the occlusal surface of the tooth of more than 20 N.

When the measurements and the simulations on a flat model of the prosthesis, it was found that, regardless of location (tooth) applying forces to values of 15 N in both the deflection and deformation of the metal plate of the prosthesis are linear.

In models of dental prostheses estimated value of deflection should not exceed 5 mm [6]. The values of deformations that occur during the tests depend on the place of measurement on the prostheses. In further discussion it was assumed that within the range of ±300 µm/m. The bench afforded the opportunity to significantly expand the ranges so that the measurements were possible for the values of external forces to 20-25 N [7, 8].

2. Cast partials testing

Research effort was channelled into conducting a numerical analysis of cast partials under dynamic load. The specimen (Fig. 1) used for analysis was a replica of an intraoral prosthesis – a partial denture replacing six teeth and worn by a partially edentulous patient.

Fig. 2 illustrates a purpose-built test station designed to determine and measure model prosthesis’ responses to dynamic load. At the design stage, emphasis was put on facilitating carrying out diagnostic measurements [9] as well as reliability (that also meant taking into account electromagnetic interference [10, 11]) through putting in place adequate reliability structures [12, 13].

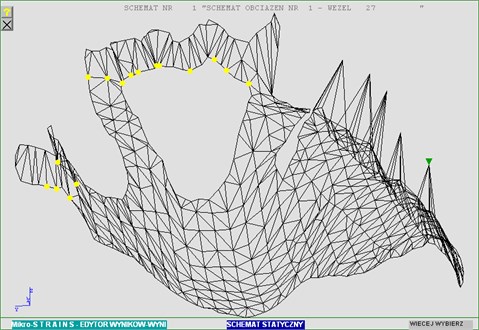
In order to validate empirical measurements taken during tests a numerical analysis of the prosthesis was carried out using the finite element method. Fig. 3 illustrates the discretized system (division into finite triangular subregions).

Fig. 1Test prosthesis with highlighted load application points (23-27)

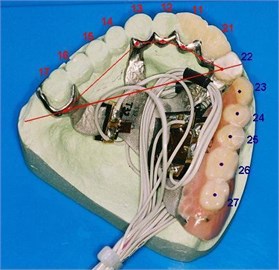
Fig. 2Diagram of test station

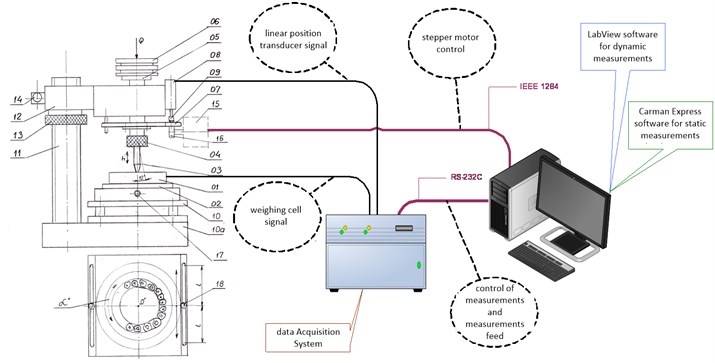
Fig. 3FEM mesh – showing both supporting nodes and nodes with prescribed loads

The model prosthesis was cast from Wironit Extra-hard-denture alloy for combination work (certificate 82593, CE 0044 ISO 6871-1).

Fig. 4Deformation distribution under the first natural frequency

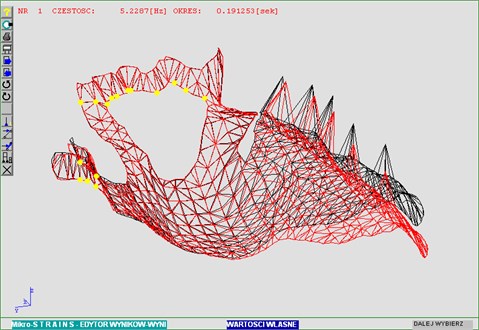
Fig. 5Prosthesis deformation distribution for t= 0.5 sec.

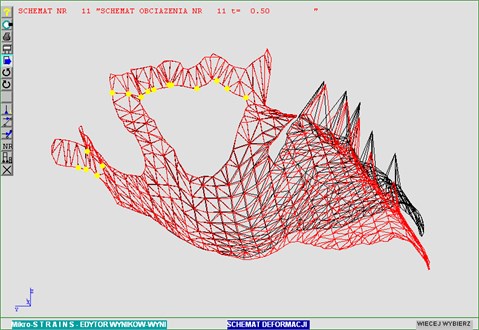
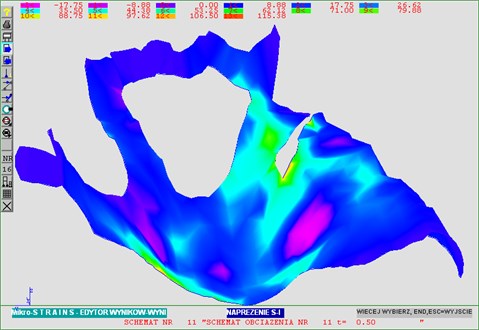
Fig. 6Main stress distribution

Load bearing parameters required for numerical analysis are as follows:

– Elastic modulus: $E=$ 170000 N/mm²;

– Poisson ratio: $\nu =$0.3;

– Alloy density: $\gamma =$ 8.2 g/cm³.

The units used for calculations were consistent throughout – [mm], [N]. Natural vibration of the prosthesis was analysed first (Fig. 4).

The model prosthesis is a “fine-tuned” system. This guarantees that neither natural vibration would be within the range of assumed harmonic vibrations. Further computations and simulations validated that.

Numerical analysis of displacements was carried out with test load applied to node 27 (Figs. 1 and 3) – causing greatest deflection of the prosthesis. Out of necessity, only the results for maximum deflections were compared.

Figs. 5 and 6 illustrate deformation and state of stress under maximum stress applied.

3. Conclusions

This paper discusses issues related to arch cast partials. Completed numerical analyses of the partial denture using the finite element method validated measurements taken at the test station. Consequently, the taken assumptions were validated as well as the protocol followed for taking measurements and the simulation. Plans for further research include developing dedicated, proprietary software which would expand capabilities of the Mikro-Strains System.