Degradation and acceleration modeling for ball bearings based on kurtosis of vibration data

1. Introduction

Bearing has been occupying such an extremely significant position in many mechanical products that its healthy status may produce an enormous impact on safe operation as well as lifetime of these products. Therefore, continuous condition monitoring and accurate reliability analysis implemented on bearings will enjoy great theoretical significance and engineering application value.

Since vibration data contain rich information that characterizes bearings’ health status, analysis based on them is frequently applied in prognostics and health management (PHM) activities for bearings. However, raw vibration data are always chaotic, which is caused by noises from various sources. Feature extraction proves to be an effective way in reducing the impact of these noises, which, as its name implies, is to extract some typical features that are capable of representing health status of bearings from raw vibration data, and by analyzing their trends, we may make reasonable judgments about bearings’ health status.

In the actual environment, bearings are usually operating under different stress levels, which leads to different degradation and failure behaviors. ADT can be utilized for degradation data collection and analysis in which items are subjected to elevated levels of stress to accelerate the performance degradation process. Proper accelerated models should be correctly selected or established in order to find out the quantitative relationship between degradation behaviors and stress levels.

In this article, degradation model is established in section 3 according to the feature extraction results in section 2. Next, Section 4 mainly discusses the construction of accelerated model that illuminates the correlation between the shape parameter of degradation model and two common kinds of stress. Reliability analysis based on Wiener process and previous results is carried out subsequently. Section 5 contains some conclusions plus some ideas for further work. The architecture of our research can be illustrated by Fig. 1.

Fig. 1Architecture of research contents

2. Feature extraction

Feature extraction aims to analyze some typical features extracted from vibration data for that these features may show regular trends, which are much easier to model. Vibration features mainly fall into two categories. Time domain features include root mean square (RMS), crest factor and kurtosis etc. Frequency domain features include mean square frequency etc. It must be noted that different types of features are suitable for different occasions so that selecting appropriate features is an issue of leading position and crucial importance during vibration data processing.

2.3. Extraction of kurtosis and data smoothing

After extracting some typical features from band-pass filtered signals, we find that the kurtosis index shows a rising trend in general. In fact, kurtosis is a rather sensitive to vibration and shock signals, which codetermines its fitness for vibration data analysis.

Kurtosis is a numerical statistic that reflects the distribution characteristics of vibration signals. For a set of discrete vibration data, kurtosis can be expressed as:

1

$K=\frac{1}{N}\sum _{i=1}^N{\left(\frac{x_i-\stackrel{-}{x}}{\sigma }\right)}^4,$

where $N$ represents the number of sampling points, $x_i$ is the vibration amplitude, $\stackrel{-}{x}$ is mean amplitude and $\sigma$ represents standard deviation. When a bearing is operating under healthy state, the amplitude distribution of vibration signals is close to normal distribution due to varieties of uncertainties, and kurtosis value is approximately equal to 3 [3]. With the emergence and development of failures, the distribution will gradually deviates from normal distribution, then kurtosis value will increase until failure.

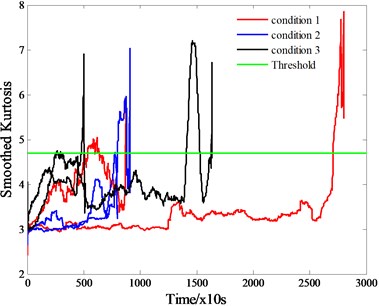
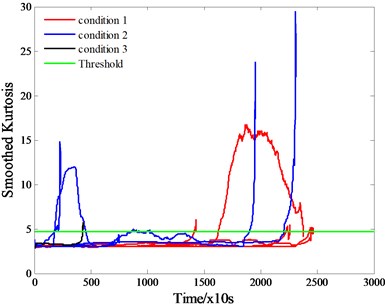
In consideration that the extracted kurtosis may enjoy fluctuations, a moving average filter method is employed to smooth the time series kurtosis in order to clearly identify trends over time [2]. Results of training bearings and test bearings are shown in Fig. 2(a) and Fig. 2(b) respectively (with moving average of 200 data points).

Fig. 2Smoothed kurtosis extracted from vibration signals of a) training bearings, b) test bearing

a)

b)

3. Degradation modeling

As shown in Fig. 2, not all of the curves show an increasing trend, such as bearing 2_3 and bearing 3_3. Elimination of these exceptions is reasonably permitted.

Degradation modeling is intended to analyze the degradation behavior of bearings before failure and try to find a model to describe the degradation process. From a visual observation of all curves shown above, we can see that in most cases, the degradation of kurtosis firstly goes through a slowly changing phase, then an abrupt change appears and bearings fail in no time. If we take the whole process to model, the inevitable deviation will be too large to accept. An alternative way is to only model the former part when kurtosis values are under a pre-defined threshold, which will offer helpful guidance for life prediction since the abrupt change is quite transitory. Therefore, the former part will be saved and used for degradation modeling, with the latter mutant part being pruned in this paper.

The threshold mentioned above should be carefully identified. There are no unified standards due to that different filter orders will lead to different extraction results. After inspecting all curves, it is reasonable to make 4.7 be a common threshold. See Fig. 2.

After inspection on characteristics of all curves, an exponential model is embedded in a Wiener process model to form the following degradation model:

where $K\left(t\right)$ is the function that describes how kurtosis value changes with time, $a$ and $b$ are fitting parameters, while $b$ can be viewed as the shape parameter of the established model which determines the concrete trend. $B\left(t\right)~N\left(0,t\right)$ represents a standard Wiener process, and $\sigma$ is diffusion coefficient. The model can be simplified by taking an expectation on both sides of the equal sign:

where $K$ represents expectation of kurtosis at each time point. According to this model, we are able to obtain ideal degradation trends under various stress levels.

A regression analysis is conducted on the smoothed time series to identify model coefficients. To improve fitting accuracy, model Eq. (3) is transformed to logarithmic form:

where $\mathrm{l}\mathrm{o}\mathrm{g}$ represents natural logarithm.

With the purpose of effectively eliminating the abnormal conditions, a two-step screening process is implemented. The first screening is according to the value of $b$. Values that are too high or low (negative ones included) should be excluded. The second screening is based on a fitting index, R-square. R-square is the coefficient of multiple determination which measures how successful the fit is in explaining the variation of the data in order to verify the fitting accuracy. A value closer to 1 indicates a better fit. In our case, after the first screening step, the first three of the rest bearings with the highest R-square values are finally selected (two bearings of condition 3 are already foreclosed after the first elimination, so there is only one left).

Estimated model parameters and corresponding R-square values of the selected bearings is shown in Table 2.

4. Accelerated model and reliability analysis

Since the degradation model has been established, an accelerated model that describes the correlation between parameters of this degradation model and stress levels is expected, by which we are able to extrapolate the degradation behaviors under various stress levels. By calculating the mean value of $a$ and $b$ respectively under each operating condition, the following Table 3 can be obtained.

For parameter $a$, the calculated results in Table 2 are all around 3, which validates the conclusion that the kurtosis value is approximately equal to 3 when bearings are operating under healthy state. Therefore, we may reasonably make $a$ equal to 3 in the following discussion. This way, the focus in this section is to seek out the correlativity between the shape parameter $b$ and applied stresses. Here, a fixed effects linear model is adopted [4]:

where $b$ is the shape parameter, $r$ and $N$ represent rotational speed and radial load respectively, and $\mathrm{l}\mathrm{o}\mathrm{g}$ is natural logarithm, ${\beta }_0$~${\beta }_5$ are model coefficients. This model, naturally, can be used as our accelerated model.

Matrix operations can be implemented in order to find out values of the coefficients. The final result is: $\beta ={\left(\text{0, 0, –19.2890, 0, 0.0205, 2.0536}\right)}^T\text{.}$ Thus the final accelerated model can be expressed as:

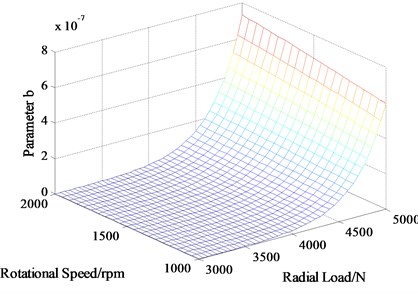
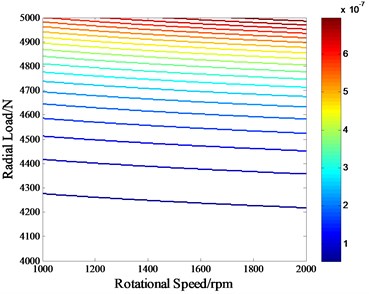
Relationship between parameter $b$ and two types of stress is shown in a three-dimensional figure, Fig. 3(a), and corresponding contour line with a color bar are drawn in Fig. 3(b). Then the degradation trend of kurtosis under normal stress level ($r=$1200 rpm, $N=$3000 N) can be obtained:

After the acquisition of degradation model Eq. (6), we are able to implement reliability analysis process under different stress levels. A linear Wiener process model is applied here:

where $K$ represents kurtosis and $K_0$ is the initial value. $\mu$ is degradation rate. Sample data are extracted every 20 time points from the ideal degradation data.

Fig. 3a) Relationship between b and two types of stress, b) corresponding contour line

a)

b)

First passage time is a critical parameter in Wiener process representing the time point when degradation curve passes through the failure threshold for the first time, which exactly equals to lifetime of the product. It is a random variable and follows Inverse Gaussian Distribution [5], and the corresponding reliability function can be expressed as:

where $C$ is the failure threshold defined before, namely 4.7, $K_0$ is the initial value, 3.0.

The reliability curves under three accelerated conditions and normal condition are drawn in Fig. 4(a) and Fig. 4(b) respectively.

Fig. 4Reliability curves under a) three accelerated conditions, b) normal condition

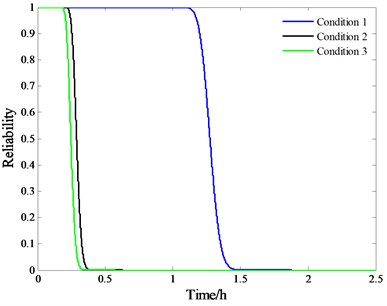
a)

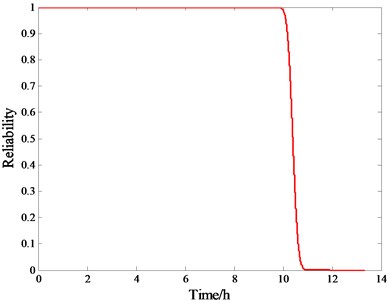
b)

5. Conclusions

This article provides a reliability analysis structure for ball bearings based on kurtosis index including a set of procedures, successively outputting degradation model, accelerated model and reliability curve, all of which may contribute to further study such as RUL prediction and failure diagnostics. However, our results are relatively ideal and inevitably divorced from reality since they are obtained using mathematical and theoretical ways. Thus, future work may focus on discussing and quantifying the uncertainties during operation that may influence the health state of bearings and finding models that are more closed to reality.