Dynamics of multi-disk shafting supported on journal bearing

1. Introduction

The micro gas turbine is the main generating sources of power and heat, which is the main development direction of distributed energy system in the world. With the development of the micro gas turbine technology, it has become the most mature and promising distributed power generation equipment. Gearbox was used to connect the generator in the conventional micro gas turbine system. It had disadvantage of low system efficiency, complex system structure and poor operational reliability, which severely restricted its use and development [1]. However, the impeller shafting was connected to high-speed permanent magnet motor directly in modern micro gas turbines, and hydrodynamic gas-lubricated bearing was used to support the rotor. The efficiency and reliability of system was greatly improved [2-3].

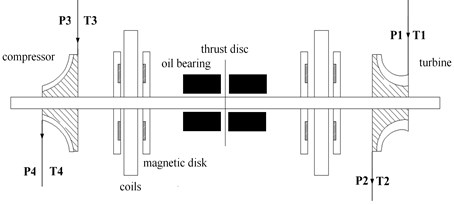
High-speed permanent magnet motor is an important part of modern micro gas turbine shafting. Its form is divided into radial magnetic field motor (conventional column type motors) and axial magnetic field motor. Currently, most of micro gas turbines used column type motors, the shafting had large span, which reduced power density and dynamics stability of the system. Disc motor is the development of axial magnetic field motor. Compared with conventional column type motor, it has advantages of large power density, large torque and small axial length, which is suitable for the impeller shafting. As shown in Fig. 1 was a schematic diagram of the shafting with four disc motors symmetrically installed. The shafting was supported by two journal bearings on both sides of the disc motors.

The rotor-bearing system supported by oil film has very strong nonlinear dynamic characteristics. Many scholars have done a lot of research in this direction. Kicinski [4] presented a method determining linear dynamic factor, and studied the nonlinear dynamic behavior of multi-span rotor system based on the finite element method. It showed self-excited vibration and forced vibration had large impact on motion stability. Brancati [5] studied axis trajectory and its corresponding stability of unbalanced rotor with the cylindrical bearings. The elastic rubbing of shafting with oil bearing was carried out by Runge-Kutta algorithm in literature [6]. Bifurcation map, Poincare map and spectral analysis were used to show dynamics of shafting. The shafting had rich dynamic phenomenas, such as periodic and quasi-periodic and chaotic behavior. Li [7] built rubbing dynamic model of a continuous rotor-bearing system considering nonlinear oil force. The influences of different parameters on the nonlinear dynamic characteristics were obtained.

The dynamics research of multi-disk shafting which was supported on middle position was not so much. The dynamic model of multi-disk shafting with oil film was established using finite element method to calculate principle modes and nonlinear dynamic response. The influences of eccentric magnitude, dynamic viscosity, bearing clearance on nonlinear dynamics were discussed. The results could provide theoretical reference for design and fault diagnosis of the shafting dynamics.

Fig. 1Disc permanent magnet motor-impeller rotor

2. Dynamic modeling of multi-disk shafting supported on journal bearing

2.1. Nonlinear dynamic equation using finite element method

Fig. 2 shows the finite element model of rotor system. Shafting left was compressor and right was turbine. Two pairs of disk type motors were mounted symmetrically on the shaft. The oil film bearings were on both sides of the thrust plate.

Fig. 2Finite element model of rotor system

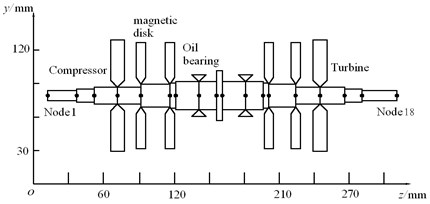
The rotor had 17 shafts and 18 nodes. The compressor and turbine were located nodes 4 and 15, and four disk type motors were located at nodes 5, 6, 13, 14. Timoshenko beam model that considering shear and gyroscopic effect was used to model the shaft. Nonlinear dynamics equations that had 72 degrees of freedom were obtained by using finite element method:

1

$M\ddot{z}+C\dot{z}+Kz=F_B\left(z,\dot{z}\right)+Q\left(t\right)+G.$

In Eq. (1), $C=D+J\omega$, $M$: Mass matrix, $C$: Damping matrix, $D$: Material damping matrix, $J$: Gyro force matrix, $\omega$ is Rotating angular velocity, $K$ is Stiffness matrix, $F_B$ is Nonlinear oil film force vector, $Q$ is Unbalanced force vector, $G$ is Gravity vector, $z$ is Displacement vector, expressed as $[x_i,y_i,-{\theta }_{x_i},-{\theta }_{y_i}{]}^T$.

The material damping of shaft is defined as Rayleigh damping:

2

$D=\alpha M+\beta K,$

where:

$\alpha =\frac{2({\xi }_2/{\omega }_{n2}-{\xi }_1/{\omega }_{n1})}{1/{\omega }_{n2}^2-1/{\omega }_{n1}^2},\beta =\frac{2({\xi }_2{\omega }_{n2}-{\xi }_1{\omega }_{n1})}{{\omega }_{n2}^2-{\omega }_{n1}^2},$

${\omega }_{n1}$, ${\omega }_{n2}$ are respectively 928.7 rad/s and 2282.1 rad/s, which are the first and second natural frequencies of the shafting with rigid bearing. ${\xi }_1$, ${\xi }_2$ are respectively 0.05 and 0.08, which are structural damping ratio.

3. Numerical simulation

For dynamic model shown in Fig. 2, the geometrical and physical parameters of system are as follows: diameter of oil bearing $D=$ 25 mm, active length of oil bearing: $L=$ 23 mm, geometric length $L_h=$35 mm, bearing clearance $c=$ 0.18 mm, oil viscosity $\mu =$ 0.018 Pa∙s. The total span of shafting is 300 mm, shaft material is 40 Cr. The radius of disk simplified for compressor and turbine is 50 mm and their thickness is 12 mm. The four magnetic disks have same physical dimension, the radius is 45 mm and the thickness is 4 mm.

Fig. 3Campbell diagram

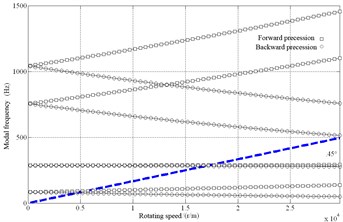
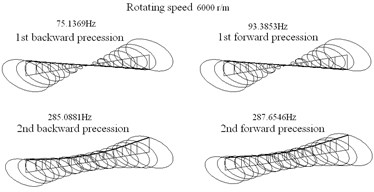
Fig. 4Principle modes of rotor

a)

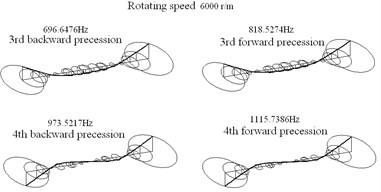
b)

3.2. The nonlinear dynamic characteristics

The Newmark-$\beta$ algorithm was used to solve nonlinear dynamic equations. The dynamic responses and stability of rotor system under different dynamic parameters were accurately calculated. The initial parameters of the oil film force: diameter of oil bearing $D=$ 25 mm, active length of oil bearing: $L=$ 23 mm, geometric length $L_h=$35 mm, bearing clearance $c=$0.18 mm, oil viscosity $\mu =$ 0.018 Pa·s. The unbalances of compressor and turbine was 1 g∙m. Integration step of the Newmark-$\beta$ algorithms was 2$\pi /$1000.

Fig. 5Bifurcation of compressor

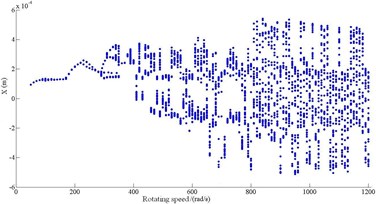
a)$x$ bifurcation

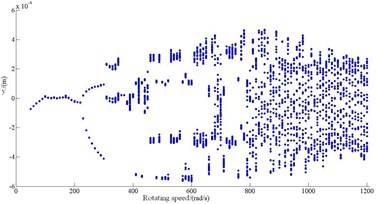
b)$y$ bifurcation

Table 1System response at e= 0.05

Rotating speed $\omega$ (rad/s)	Response	Rotating speed $\omega$ (rad/s)	Response
50-200	P-1	350-370	P-1
200-310	P-2	370-800	P-N
310-330	P-4	800-1200	Quasi-period
330-350	Quasi-period

The bifurcation characteristics of the compressor are shown in Fig. 5 when the shafting rotates from 50 rad/s to 1200 rad/s. The shafting has rich nonlinear dynamics characteristics. The motion forms of compressor in turn: P-1→P-2→P-4→Quasi-period→P-1→P-N, as shown in Table 1. From Fig. 5 it can be seen the vibration amplitude is increasing as the rotating speed increased under the action of nonlinear oil film force. The double-bifurcations occur and produce a P-2 motion when rotating speed is 200 rad/s. Then, double-bifurcations occur again, P-2 motion changes to P-4 motion. Next, inverse bifurcations happen from P-4 to P-1. With the rotating speed increasing, a wide range of P-N motion appears, and then evolves into quasi-periodic motion.

Fig. 6 shows vibration of the compressor when it rotates at 240 rad/s. The axis orbit is like inside 8 as shown in Fig. 6(a). Its Poincare map has two isolated points in Fig. 6(b), which indicates P-2 motion. The shafting appears half-frequency whirl. Fig. 7 shows vibration of the compressor when it rotates at 1180 rad/s. Its Poincare map is a closed circle, which shows quasi periodic motion.

3.2.1. The influence of eccentric magnitude

In engineering practice, the rotor inevitably has eccentric magnitude and directly affects the dynamics characteristics of the shafting. When eccentric magnitude was 0.1 mm-2.0 mm and rotating speed was 600 rad/s, the bifurcation characteristics was studied.

Fig. 8(a) shows amplitude $x$ of the compressor first increases then decreases with the increasing eccentricity. By analyzing each eccentricity and its corresponding Poincare map, the shafting presents P-N motion when eccentricity is from 0.1 mm to 0.4 mm. The shafting presents quasi-periodic motion when eccentricity is in 0.4 mm to 1.9 mm. The shafting presents P-N motion again when eccentricity is 2.0 mm. Fig. 8(b) and Fig. 8(c) shows axis orbit and its Poincare map of compressor respectively when $e=$1.3 mm.

Fig. 6Compressor vibration characteristics (ω= 240 rad/s)

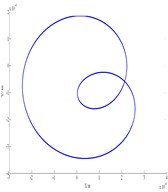
a) Axis orbit

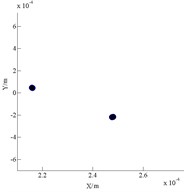
b) Poincare map

Fig. 7Compressor vibration characteristics (ω= 1180 rad/s)

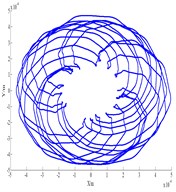
a) Axis orbit

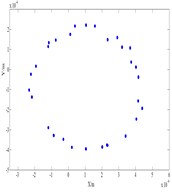
b) Poincare map

Fig. 8The influence of unbalance to bifurcation

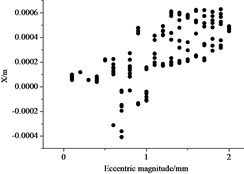
a) Bifurcation characteristics

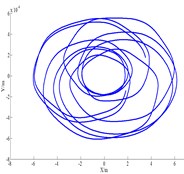
b) Axis orbit ($e=$ 1.3 mm)

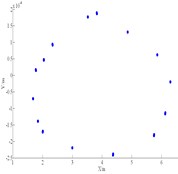
c) Poincare map

3.2.2. The influence of oil dynamic viscosity

The influence of oil brands and friction heat on dynamic viscosity is large. It is necessary to study the effect of oil dynamic viscosity on the rotor dynamics.

Fig. 9Influence of dynamical viscosity to bifurcation

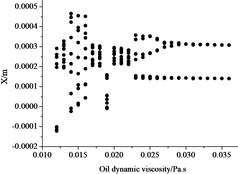
a) Bifurcation characteristics

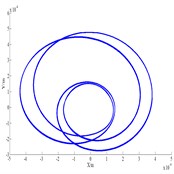
b) Axis orbit

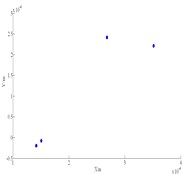
c) Poincare map

When the eccentricity was 1 mm and dynamic viscosity of lubricating oil was from 0.012 Pa∙s-0.036 Pa∙s, bifurcation characteristics of the shafting were investigated when rotating speed was 400 rad/s. It can be seen from Fig. 9(a), with the increasing of dynamic viscosity, the vibration amplitude decreases. When $\mu =$ 0.012 Pa∙s, the shafting presents P-13 motion. When $\mu$ is from 0.012 Pa∙s to 0.022 Pa∙s, the shafting presents quasi-periodic motion. Then, with $\mu$ becoming larger, quasi-periodic motion is gradually transformed into P-8→P-6→P-4→P-5→ P-4→P-2 motion. Generally speaking, larger dynamic viscosity will help to improve the stability of the shafting. Fig. 9(b) and Fig. 9(c) are axis orbits and Poincare map of compressor respectively when $\mu =$ 0.025 Pa∙s, the Poincare map shows P-4 motion.

3.2.3. The influence of the bearing clearance

In engineering practice, the bearing clearance is variable, even the assembly error also cause the change of the bearing clearance. When the eccentricity was 1 mm and the bearing clearance $c$ was from 0.12 mm-0.36 mm, bifurcation characteristics of the shafting were investigated when rotating speed was 800 rad/s.

It can be seen from Fig. 10(a), with the increasing of the bearing clearance, the vibration amplitude increases. When $\delta$ is from 0.12 mm to 0.18 mm, the shafting presents P-N motion. $\delta$ is from 0.18 mm to 0.36 mm, the shafting presents quasi-periodic motion. This shows larger bearing clearance reduces the dynamic stability of the shafting.

Fig. 10Influence of bearing clearance to bifurcation

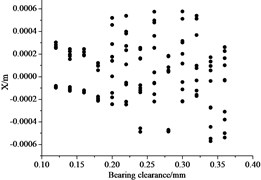
a) Bifurcation characteristics

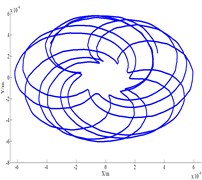
b) Axis orbit ($\delta =$ 0.36 mm)

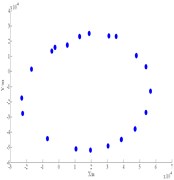
c) Poincare map

4. Conclusions

1. When the bearing stiffness of rotor system is about 7×10⁶ N/m, and its damping is 200 N∙s/m. Based on the Campbell diagram, the shafting has two critical speeds 5,500 r/m and 17,500 r/m within 30,000 r/m.

2. The vibration amplitude is increasing as the rotating speed increases under the action of nonlinear oil film force. The double-bifurcations occur and produce a P-2 motion when rotating speed is 200 rad/s. Then, double-bifurcations occur again, P-2 motion changes to P-4 motion. Next, inverse bifurcations happen from P-4 to P-1. With the rotating speed increasing, a wide range of P-N motion appeares, and then evolves into quasi-periodic motion. The larger dynamic viscosity will help to improve the stability of the shafting.

3. The vibration amplitude of the compressor first increases then decreases with the increasing eccentricity. The shafting presents P-N motion, quasi-periodic motion and P-N motion again. The larger bearing clearance reduces the dynamic stability of the shafting.