Analysis of the effect of squeeze film damper on the bending-torsional coupling vibration characteristics of dual-rotor system

Jin, Zhu; Chen, Moli; Luo, Gui-Huo; Yue, Lin

doi:10.21595/vp.2022.22902

Vibroengineering Procedia

Browse Procedia

Published: 22 October 2022

Check for updates

Analysis of the effect of squeeze film damper on the bending-torsional coupling vibration characteristics of dual-rotor system

Zhu Jin¹

Moli Chen²

Gui-Huo Luo³

Lin Yue⁴

^{1, 4}Nanjing University of Aeronautics and Astronautics, College of Mechanical and Electrical Engineering, Nanjing, 210016, China

^{2, 3}Nanjing University of Aeronautics and Astronautics, College of Energy and Power Engineering, Nanjing, 210016, China

Corresponding Author:

Moli Chen

Cite the article Download PDF

Downloads 261

Abstract

The study of the vibration reduction characteristics of SFD to the bending-torsional coupled vibration of the dual-rotor system can provide support for the structural design of aero-engines. Based on the overall eccentric disc model, the bending-torsional coupling dynamic equation of the dual-rotor system is established in this paper. The amplitude and nonlinear periodic characteristics of the dual-rotor system are obtained by combining Newmark-β method and Newton-Raphson method. The results show that the vibration reduction effect of SFD on bending-torsional coupling vibration is closely related to the speed. The vibration reduction effect of SFD is weak at the first-order critical speed range and below, and reduces the torsional amplitude by 70 % at the second-order critical speed range and above. SFD kept the bending-torsional coupling vibration of the dual-rotor system stable in a stable 5-period motion state.

Analysis of the effect of squeeze film damper on the bending-torsional coupling vibration characteristics of dual-rotor system

Highlights

The bending-torsional coupling vibration model of a dual-rotor system is established based on the eccentric disc.
The vibration reduction performance of SFD to bending-torsional coupling vibration is closely related with the speed. In the first-order critical speed range and below, SFD has weak damping effect. At the second-order critical speed range and above, SFD reduces the maximum bending amplitude of the inner and outer rotors by 40% and the maximum torsional amplitude by 70%.
SFD can improve the periodic characteristics of bending-torsional coupling vibration response. Compared with the periodic characteristics without SFD, SFD keeps the bending-torsional coupling vibration of the dual-rotor system in a stable 5-period motion state.

1. Introduction

Squeeze Film damper (SFD) are the main vibration damping components in the aero-engine rotor system, which can effectively suppress the vibration of the rotor system, improve the stability of the rotor system and extend the service life of the aero-engine. With the wide application of SFD in rotor systems, the study of the influence of SFD on the dynamic characteristics of the rotor systems has become an important topic for many scholars.

Jawaid I. Inayat-Hussain investigated the effect of various design parameters on the bifurcation response of an elastic rotor supported and an SFD containing cage support. The results show that the onset rotational speed of the bifurcation increases with the increase of stiffness ratio and decreases with the increase of mass ratio [1]. S. Dănăilă and L. Moraru discussed the classical theory of hydraulic lubrication in SFD research, pointing out its limitations. It is pointed out that the oil film in the SFD is only directly affected by the precession and nutation of the rotor, but in the classical theory, the flow in the thin film is also governed by the Reynolds equation [2]. Shan et al. established a rotor experimenter with SFD, and studied the vibration reduction characteristics of SFD to the vibration caused by rubbing and misalignment faults by means of experiments [3]. Wang Jun et al. studied the control of the chaotic motion of the failed rotor system by establishing the SFD-rotor- rolling ball bearing system dynamics model under the misalignment-touch-friction coupling [4]. Hamidreza Heidari and Mohammadreza Ashkooh studied the stability and bifurcation properties of SFD-rotor systems. The results show that the unsymmetrical stiffness of squeeze film dampers in the presence of cavitation promoting the chance of undesirable nonsynchronous vibrations [5]. LIU Yang et al. analyzed the damping performance of SFD in rotor system from the theoretical point of view, and the results show that SFD can reduce the vibration amount of rotor at certain speed range, and the damping effect is not good at relatively low speed [6]. Shin D. et al. established an SFD model considering fluid inertia factors and cavitation effects, and applied it to the rotor model based on Euler beams. The simulation results show that SFD suppresses the vibration caused by the Morton effect [7]. Vincent Iacobellis et al. studied the effect of squeeze film clearance and oil inlet configuration on the unbalanced response of Jeffcott rotor by experiments. The results show increased damping with smaller clearance and increased number of oil inlets, while the number and orientation of oil inlets also show an effect on the level of air ingestion into the SFD and some asymmetry in the rotor response [8]. Based on Reynolds boundary conditions, Xu Weiwen et al. derived the oil film force characterization equation of the squeeze film damper under static eccentricity condition and analyzed the effect of static eccentricity on the vibration damping characteristics of the squeeze film damper [9]. Wang Haifei established a rotor system with the fit looseness fault and studied the vibration reduction effect of squeeze film damper on the rotor system with the fit looseness fault. The results showed that the squeeze film damper can reduce nonlinear vibration responses effectively generated by the fit looseness fault for the nonlinear contact [10].

In recent years, with the continuous improvement of aero-engine performance, the rotor speed is getting higher and higher, and the aspect ratio is getting larger and larger, the vibration characteristics of the rotor system also change, and its bending vibration and torsional vibration are coupled, i.e. bending-torsional coupling vibration. At present, there are relatively few studies on the bending-torsional coupling vibration characteristics of rotor system, and the model is relatively simple. In this paper, the SFD-intermediate bearing-dual rotor system is used as a model for the first time to study the effect of SFD on the bending-torsion coupling vibration characteristics of the dual-rotor system by simulation. Through calculational simulation, reasonable structural parameters can be obtained to provide important support for the structural design of the rotor system, and it can help us understand the influence of SFD on the bending-torsional coupling vibration of the dual-rotor system, which has important guiding significance for further experiments and research.

In this paper, the differential equations of motion containing local nonlinearity for the SFD-intermediate bearing-dual rotor system are derived using the Lagrange equation and the finite element method. And they are solved using a numerical integration method combining the Newmark- $β$ method and the Newton-Raphson method to analyze the effect of SFD on the bending-torsion coupling vibration characteristics of the dual-rotor system.

2. Mathematical model

The dual-rotor model is shown in Fig. 1, which is supported by five pivots with 1-1-1 for the inner rotor support scheme and 1-0-1 for the outer rotor support scheme. Inner rotor contains disk 1, disk 4, bearing I (including SFD1), bearing II, and bearing V. Outer rotor contains disk 2, disk 3, and bearing III; bearing IV is an intermediary bearing, which connects the inner rotor and outer rotor.

In this paper, the bending-torsional coupling vibration of the dual rotor is predicated on the existence of an eccentric mass of the disk, so the overall eccentric disk model is needed. To describe the motion of the disk in the dual-rotor system, a rotor coordinate system is established as shown in Fig. 2. The coordinate system $o x y z$ is the overall coordinate system, and the coordinate system $o' ξ ζ η$ is the local coordinate system of the disk, which moves together with the disk.

By using Lagrange equation, the motion differential equation of the 5-DOF integral eccentric disc element can be obtained:

1

M_{d} {\ddot{q}}_{d} + (C_{d} + Ω G_{d}) {\dot{q}}_{d} + K_{d} q_{d} = F_{d},

M_{d} = [\begin{matrix} m_{d} & 0 & 0 & 0 & - m_{d} e s i n (Ω t + φ) \\ 0 & m_{d} & 0 & 0 & m_{d} e c o s (Ω t + φ) \\ 0 & 0 & I_{d} & 0 & 0 \\ 0 & 0 & 0 & I_{d} & 0 \\ - m_{d} e s i n (Ω t + φ) & m_{d} e c o s (Ω t + φ) & 0 & 0 & I_{p} + m_{d} e^{2} \end{matrix}],

C_{d} = - 2 Ω [\begin{array}{l} 0 & 0 & 0 & 0 & m_{d} e c o s (Ω t + φ) \\ 0 & 0 & 0 & 0 & m_{d} e s i n (Ω t + φ) \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}], G_{d} = [\begin{array}{l} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & I_{p} & 0 \\ 0 & 0 & - I_{p} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}],

K_{d} = [\begin{array}{l} 0 & 0 & 0 & 0 & m_{d} e Ω^{2} s i n (Ω t + φ) \\ 0 & 0 & 0 & 0 & m_{d} e Ω^{2} c o s (Ω t + φ) \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}], F_{d} = [\begin{matrix} m_{d} e Ω^{2} c o s (Ω t + φ) \\ m_{d} e Ω^{2} s i n (Ω t + φ) \\ 0 \\ 0 \\ 0 \end{matrix}],

where $m_{d}$ , $e$ , $I_{d}$ and $I_{p}$ are the mass, eccentricity, diameter rotational inertia and polar rotational inertia of the disk. $q_{d}$ is the displacements of generalized degrees of freedom for the disk. $Ω$ is the rotor speed, and $φ$ is the initial phase angle. $M_{d}$ , $C_{d}$ , $G_{d}^{}$ and $K_{d}$ are the inertia matrix, damping matrix, gyroscopic matrix and stiffness matrix of the 5-DOF disk with eccentric mass, respectively, and $F_{d}$ is the unbalance force caused by the eccentric mass. From the matrices of $M_{d}$ , $G_{d}^{}$ and $K_{d}$ , it can be found that there is a coupling term between the bending direction and torsion direction of the disk, and the coupling term is a function of $e$ . It can be concluded that the mass eccentricity of the disk can induce the bending-torsion coupling vibration.

Fig. 1SFD-intermediate bearing-dual rotor model

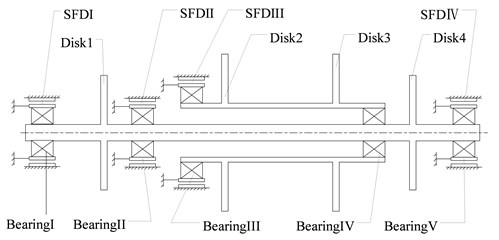
Fig. 2Rotor coordinate system

The nonlinear oil film force of SFD can be derived using the short bearing assumption and Reynolds boundary conditions, and the components of the oil film nonlinear force in the $x$ and $y$ directions are as follows:

2

\{\begin{array}{l} f_{x}^{s f d} = - \frac{μ R L^{3}}{c^{2} {(x^{2} + y^{2})}^{1 / 2}} [x (\dot{ε} I_{2} + ε \dot{ψ} I_{1}) + y (\dot{ε} I_{1} + ε \dot{ψ} I_{3})], \\ f_{y}^{s f d} = - \frac{μ R L^{3}}{c^{2} {(x^{2} + y^{2})}^{1 / 2}} [y (\dot{ε} I_{2} + ε \dot{ψ} I_{1}) - x (\dot{ε} I_{1} + ε \dot{ψ} I_{3})], \end{array}

ε = \frac{\sqrt{x^{2} + y^{2}}}{c}, \dot{ε} = \frac{x \dot{x} + y \dot{y}}{c \sqrt{x^{2} + y^{2}}}, \dot{ψ} = \frac{y \dot{x} - x \dot{y}}{x^{2} + y^{2}}, t a n ψ = \frac{x}{y},

where $x$ and $y$ are the projections of the oil film journal eccentricity in the rotor coordinate system, $L$ , $R$ , $c$ , and $ε$ denote the length, radius, radial clearance and journal eccentricity of the SFD, respectively. $μ$ is the dynamic viscosity coefficient of oil, $ψ$ is the precession angular displacement of the center of the oil film journal around the center of the oil film ring, respectively. $I_{j}$ ( $j =$ 1, 2, 3) represents the Sommerfeld integral.

The rotor uses a 5-DOF Timoshenko beam element considering shear deformation and rotational inertia, and the intermediary bearing model uses a nonlinear force model of the bearing from the literature [11]. Using finite element theory, the mass matrix, damping matrix, gyroscopic matrix and stiffness matrix of the disk and beam units are assembled to obtain the differential equations of motion for the SFD- intermediary bearing- dual rotor system as follows:

3

M \ddot{q} + (C + Ω G) \dot{q} + K q = F_{u} + Q,

where $M$ , $C$ , $G$ , and $K$ are the inertia matrix, damping matrix, gyroscopic matrix and stiffness matrix of the dual-rotor system, respectively. $q$ is the displacements of generalized degrees of freedom for the rotor system. $F_{u}$ is the unbalance force of the dual-rotor system, and $Q$ is the generalized external force acting on the rotor system, including the intermediary bearing nonlinear force and the SFD nonlinear force.

3. Results and discussion

3.1. Bending-torsional coupling vibration amplitude characteristics

In this paper, we compare the bending-torsional coupling vibration characteristics of the dual-rotor system with and without SFD for the inner rotor disk 4 and the outer rotor disk 3.

Fig. 3Vibration amplitude characteristics graph

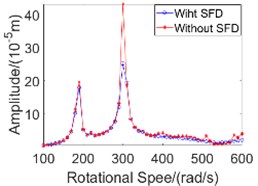
a) Disc 4 bending vibration amplitude

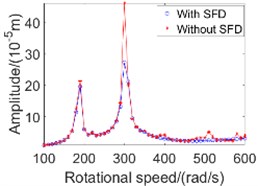
b) Disc 3 bending vibration amplitude

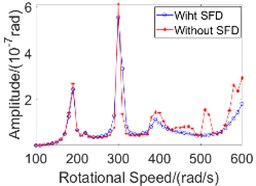
c) Inner rotor torsional vibration amplitude

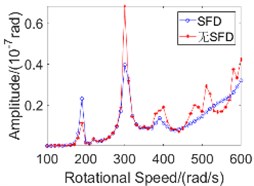
d) Outer rotor torsional vibration amplitude

The vibration amplitudes of the inner and outer rotors of the dual-rotor system are shown in Fig. 3. In the range of 100 to 600 rad/s, the dual-rotor system passed two orders of critical speed, 190 rad/s and 300 rad/s, respectively.

For bending vibration, it can be seen from Fig. 3(a) and Fig. 3(c) that the effect of SFD on the bending vibration response amplitude of the dual-rotor system is weak in the speed range of the first-order critical speed and below. In the speed range above the first-order critical speed, the effect of SFD on the bending vibration response amplitude of the dual-rotor system is obvious, especially near the second-order critical speed, and the maximum reduction of bending vibration amplitude of the dual-rotor system using SFD is 40 % compared with the without SFD condition.

Fig. 4Inner rotor disc 4 Poincare diagram

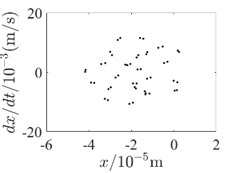
a) 400rad/s-without SFD

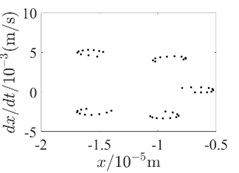
b) 500rad/s-without SFD

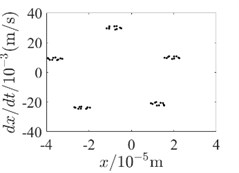
c) 600rad/s-without SFD

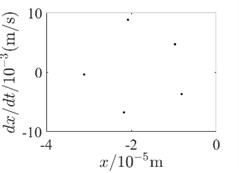
d) 400rad/s-with SFD

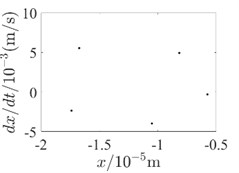
e) 500rad/s-with SFD

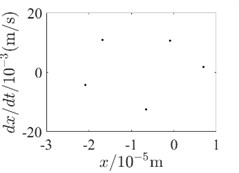
f) 600rad/s-with SFD

Fig. 5Outer rotor disc 3 Poincare diagram

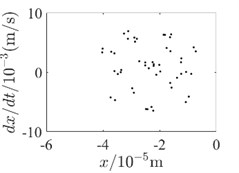
a) 400 rad/s-without SFD

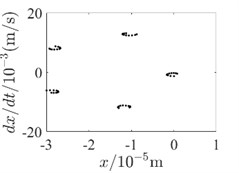
b) 500 rad/s-without SFD

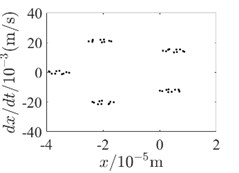
c) 600 rad/s-without SFD

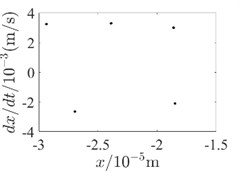
d) 400 rad/s-with SFD

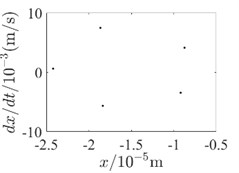
e) 500 rad/s-with SFD

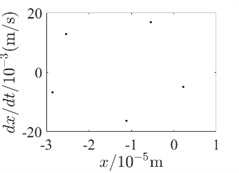
f) 600 rad/s-with SFD

For torsional vibration, Fig. 3(b) and Fig. 3(d) show the amplitude variations of torsional vibration of the inner and outer rotors, respectively. Due to the bending-torsional coupling effect, the torsional vibration of the inner and outer rotors also has peaks at the critical speed of 190 rad/s and 300 rad/s. Comparing Fig. 3(b) and Fig. 3(d), because the length-to-diameter ratio of the outer rotor is much larger than that of the inner rotor, it can be found that the amplitude of torsional vibration of the outer rotor is much smaller than that of the inner rotor, and does not exceed 1/7 of the amplitude of torsional vibration of the inner rotor. In the range of the first-order critical speed and below, the damping effect of SFD on torsional vibration is weak, even near the first-order critical speed, which makes the amplitude of torsional vibration of the outer rotor. In the speed range above the first-order critical speed, SFD has obvious effect on the amplitude of torsional vibration of the dual-rotor system, the curve is smoother and the amplitude is significantly smaller, and the vibration reduction amplitude is the largest at 510 rad/s, reaching 70 %.

As can be seen from Fig. 3, due to the bending-torsional coupling effect, the bending vibration and torsional vibration of the dual-rotor system affect each other, and the amplitude characteristics are highly similar. By analyzing the vibration amplitude of the dual-rotor system, the vibration damping performance of SFD is consistent with the conclusions obtained from the literature [6], and SFD does not have the effect of vibration damping under any speed range. SFD has a good inhibitory effect on the bending-torsional coupling vibration amplitude of dual rotors in the high speed range, which can effectively reduce the fluctuation of bending-torsional coupling vibration amplitude and make the amplitude change smoother.

4. Nonlinear periodic characteristics

In order to be able to analyze the effect of SFD on the periodicity of the dual-rotor system in detail, the vibration response data at the inner rotor disk 4 and the outer rotor disk 3 are used to draw the Poincare diagram for illustration, as shown in Fig. 4 and Fig. 5. Since SFD has a good damping crossover in the second-order critical speed range of the dual-rotor system and above, Poincare diagrams of 400 rad/s, 500 rad/s and 600 rad/s are selected, respectively. Comparing the two conditions with and without SFD, it is found that the bending-torsional vibration of the dual-rotor system with SFD condition is basically in the 5-period motion state. And the periodicity of the bending-torsional vibration of the dual-rotor system without SFD condition varies with the speed of the dual-rotor system, which is basically in the quasi-periodic motion state.

5. Conclusions

In this paper, the bending-torsional coupling vibration model of a dual-rotor system is established based on the eccentric disc. For the two conditions without SFD and with SFD, the Newmark-β method and Newton-Raphson method are combined to solve the dynamic response, and the influence on the amplitude and periodic characteristics of the bending-torsional coupling vibration of the double-rotor system is obtained. The results show that the vibration reduction performance of SFD to bending-torsional coupling vibration is closely related with the speed. In the first-order critical speed range and below, SFD has weak damping effect. At the second-order critical speed range and above, SFD reduces the maximum bending amplitude of the inner and outer rotors by 40 % and the maximum torsional amplitude by 70 %. SFD can improve the periodic characteristics of bending-torsional coupling vibration response. Compared with the periodic characteristics without SFD, SFD keeps the bending-torsional coupling vibration of the dual-rotor system in a stable 5-period motion state.

References

J. I. Inayat-Hussain, “Bifurcations in the response of a flexible rotor in squeeze-film dampers with retainer springs,” Chaos, Solitons and Fractals, Vol. 39, No. 2, pp. 519–532, Jan. 2009, https://doi.org/10.1016/j.chaos.2007.01.086

Publisher
S. Dănăilă and L. Moraru, “On the validity of the classical hydrodynamic lubrication theory applied to squeeze film dampers,” IOP Conference Series: Earth and Environmental Science, Vol. 12, No. 1, p. 012104, Aug. 2010, https://doi.org/10.1088/1755-1315/12/1/012104

Publisher
X. Sang, M. Liao, and W. Li, “Experimental study on the damping performance of squeeze film damper in rotor with faults,” (in Chinese), Journal of Vibration, Measurement and Diagnosis, Vol. 35, No. 5, pp. 977–980, 2015.

Search CrossRef
J. Wang, L. Ma, J. Zhang, and X. Lu, “Dynamic characteristics and chaos control of rotor system with faults under SFD,” (in Chinese), Journal of Vibration, Measurement and Diagnosis, Vol. 36, No. 3, pp. 541–548, 2016.

Search CrossRef
H. Heidari and M. Ashkooh, “The influence of asymmetry in centralizing spring of squeeze film damper on stability and bifurcation of rigid rotor response,” Alexandria Engineering Journal, Vol. 55, No. 4, pp. 3321–3330, Dec. 2016, https://doi.org/10.1016/j.aej.2016.08.013

Publisher
Y. Liu, T. Shi, X. Xin, Y. Ma, Z. Xue, and S. Ming, “Theoretical study on the damping efficiency of squeeze film damper on rotor,” (in Chinese), Journal of Mechanical Engineering, Vol. 55, No. 3, pp. 90–98, 2019.

Publisher
D. Shin, A. B. Palazzolo, and X. Tong, “Squeeze film damper suppression of thermal bow-Morton effect instability,” Journal of Engineering for Gas Turbines and Power, Vol. 142, No. 12, pp. 1–14, 2020.

Publisher
V. Iacobellis, K. Behdinan, D. Chan, and D. Beamish, “Effect of hole feed system on the response of a squeeze film damper supported rotor,” Tribology International, Vol. 151, p. 106450, Nov. 2020, https://doi.org/10.1016/j.triboint.2020.106450

Publisher
W. Xu, D. Zhang, P. Wang, J. Liu, Q. Fei, and D. Jiang, “Effects of static eccentricity of squeeze film damper on vibration reduction effect of rotor system,” (in Chinese), Journal of Vibration and Shock, Vol. 40, No. 21, pp. 55–61, 2021.

Search CrossRef
H. Wang, “Passive vibration reduction of a squeeze film damper for a rotor system with fit looseness between outer ring and housing,” Journal of Low Frequency Noise, Vibration and Active Control, Vol. 40, No. 3, pp. 1473–1492, 2021.

Publisher
H. Zhou, G. Luo, G. Chen, and F. Wang, “Nonlinear dynamic analysis of a rotor supported on the ball bearings with squeeze film dampers,” (in Chinese), Mechanical Science and Technology for Aerospace Engineering, Vol. 32, No. 4, pp. 499–505, 2013.

Search CrossRef

About this article

Received

26 August 2022

Accepted

12 September 2022

Published

22 October 2022

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2022.22902

Keywords

squeeze film damper

dual rotor system

bending-torsional coupling vibration

vibration reduction characteristics

periodic characteristics

Acknowledgements

The research is supported by “National Science and Technology Major Project (J2019-IV-004-0071)” and “Basic Scientific Research Business Expenses of Central Universities (56XAA20064)”.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Next article in issue Next

Research article

2023 05 18

Dynamic characteristics analysis of a coaxial rotor system with shared bearing bore structure

Yu Lu, Zhen Huan Tang, Fei Wang

Research article

2020 09 11

Numerical simulation and influence factors analysis for dynamic characteristics of squeeze film damper

Hai-Lun Zhou, Xi Chen, Chen-Shuai Zhang

Research article

2019 10 19

Research on the dynamic characteristics of the squeeze film damper of a certain aero-engine

Xue-Min Liao, Gui-Huo Luo, Zhao-Jun Feng, Li-Jia Chen, Nan Zheng

Research article

2019 03 31

Experimental study of IERSFDs for vibration reduction of gear transmissions

Kaihua Lu, Lidong He, Wei Yan

Z. Jin, M. Chen, G.-H. Luo, and L. Yue, “Analysis of the effect of squeeze film damper on the bending-torsional coupling vibration characteristics of dual-rotor system,” Vibroengineering PROCEDIA, Vol. 45, pp. 1–7, Oct. 2022, https://doi.org/10.21595/vp.2022.22902

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.22902
UR  - https://doi.org/10.21595/vp.2022.22902
TI  - Analysis of the effect of squeeze film damper on the bending-torsional coupling vibration characteristics of dual-rotor system
T2  - Vibroengineering PROCEDIA
AU  - Jin, Zhu
AU  - Chen, Moli
AU  - Luo, Gui-Huo
AU  - Yue, Lin
PY  - 2022
DA  - 2022/10/22
PB  - JVE International Ltd.
SP  - 1-7
VL  - 45
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Jin_2022,
	doi = {10.21595/vp.2022.22902},
	url = {https://doi.org/10.21595/vp.2022.22902},
	year = 2022,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {45},
	pages = {1--7},
	author = {Zhu Jin and Moli Chen and Gui-Huo Luo and Lin Yue},
	title = {Analysis of the effect of squeeze film damper on the bending-torsional coupling vibration characteristics of dual-rotor system},
	journal = {59th International Conference on Vibroengineering in Dubai, United Arab Emirates, October 22, 2022}
}

Copy Bibtex

Copied to clipboard!

[1]Z. Jin, M. Chen, G.-H. Luo, and L. Yue, “Analysis of the effect of squeeze film damper on the bending-torsional coupling vibration characteristics of dual-rotor system,” Vibroengineering PROCEDIA, vol. 45, pp. 1–7, Oct. 2022, doi: 10.21595/vp.2022.22902.

Copy IEEE

Copied to clipboard!

Jin, Zhu, Moli Chen, Gui-Huo Luo, and Lin Yue. “Analysis of the Effect of Squeeze Film Damper on the Bending-Torsional Coupling Vibration Characteristics of Dual-Rotor System.” Vibroengineering PROCEDIA 45 (October 22, 2022): 1–7. https://doi.org/10.21595/vp.2022.22902.

Copy Chicago

Copied to clipboard!

Analysis of the effect of squeeze film damper on the bending-torsional coupling vibration characteristics of dual-rotor system

Abstract

Highlights

1. Introduction

2. Mathematical model

3. Results and discussion

3.1. Bending-torsional coupling vibration amplitude characteristics

4. Nonlinear periodic characteristics

5. Conclusions

References

About this article

Related Articles