Effects of misalignment on the nonlinear dynamics of a two-shaft rotor-bearing-gear coupling system with rub-impact fault

2.1. Misaligned gear coupling

When the gear coupling is misaligned, the male and female couplings are not concentric (as shown in Fig. 1). The gear teeth on one side tightly mesh with the sleeve while those on the other side contact loosely. In this condition, the meshing force can be divided into: (a) the meshing force associated with torque and (b) the meshing force associated with dynamic vibration.

a) Meshing force associated with torque.

When the gear teeth are in contact with the sleeve to transmit a torque, the meshing force is affected by three factors: the torque-induced deformation, the meshing distance and the meshing stiffness. According to [7], the meshing force caused by the torque can be obtained:

where $F_g^T$ is the meshing force associated with torque, ${\varphi }_g$ is the deformation angle of gear tooth, $l_g$ is the equivalent meshing distance of gear tooth, and $k_g$ is the meshing stiffness of gear tooth. The ${\varphi }_g$ of all the gear teeth are identical under a static driven torque.

b) Meshing force associated with vibration.

During the torque transmission, the vibration of the rotor system leads to a relative movement between the meshing tooth and sleeve. The meshing force associated with vibration can be expressed as:

where $F_g^D$ is the meshing force caused by vibration, ${\phi }_g$ is the position angle of gear tooth, and $e_g$ is the misalignment of gear coupling.

Without torque the meshing force is zero and independent to the vibration displacement. Since the meshing force cannot be negative, the total meshing force of the $i$th tooth can be expressed as:

The meshing forces in the $y$ and $z$ directions are as follows:

c) Misalignment force

In this study, the misalignment takes place at the gear coupling and produces two forces affecting the dynamic characteristics of the rotor system: the meshing force and the misalignment force. The misalignment forces in the $y$ and $z$ directions of the rotor system are expressed as [11]:

where $y_s$ and $z_s$ are the movements of the intermediate tooth of gear coupling, $M_g$ is the mass of the intermediate tooth of gear coupling, $\omega$ is the angle velocity, $\psi$ is the initial phase. Since the intermediate tooth has to satisfy both couplings at the same time that misalignment occurs, its rotating angle velocity is related with the rotor speed and the orbit is a circle.

2.2. Ball bearing

The schematic diagram of the force applied on a ball bearing is shown in Fig. 2. Based on the Hertzian contact [23], the contact stiffness of the ball bearing can be determined as follows [24]:

where $k_b^H$ is the contact stiffness of ball bearing. $Q_b$ is the load of ball, $k_c$ is the contact deformation coefficient of the ball, and $F_{b,c}$ is the centrifugal force of the ball. The subscript $j$ means the $j$th rolling element.

Fig. 1The Schematic diagram of gear coupling

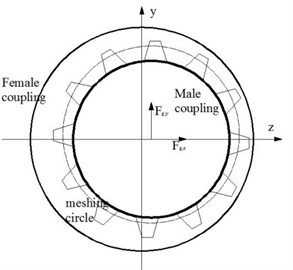
Fig. 2The Schematic diagram of ball bearing

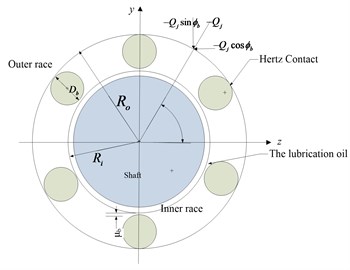
Due to the existence of oil film, the lubrication between rolling element and races should be considered. Under the EHL condition, the oil film pressure is close to Hertzian contact stress in most of the contact zone, but quite different at the entering and departing ends.

According to the pervious study [12], it is found that most of the oil film clearances in the contact zone are nearly unchanged, so the central oil film clearance can be used as equivalent. In the case of point-contact, the oil film thickness equation is suitable for the ball bearing:

where $H_b$ is the non-dimensional central oil film clearance, $U={\mu }_{b}u/2E\text{'}{R}_b$ is a non-dimensional velocity parameter, $G=\alpha E^{\text{'}}$ is a non-dimensional material parameter, $W=\frac{Q_b}{E^{\text{'}}{R}_b^2}$ is a non-dimensional load parameter, $e_b$ is the ellipticity of the rolling element, ${\mu }_b$ is the dynamic viscosity, $u$ is the linear velocity, $E^{\text{'}}=\frac{E}{{\left(1-v\right)}^2}$ is the equivalent Young’s modulus, $\upsilon$ is the Poisson’s ratio, $\alpha$ is the pressure-viscosity coefficient, and $R_b$ is the curvature radius.

Then the oil film stiffness between the rolling element and the inner race can be calculated:

The oil film stiffness between the rolling element and the outer race $k_{EHL}^o$ can be calculated in the same way. Thus, the overall oil film stiffness can be obtained:

So, the global stiffness and the radial contact load of the $j$th rolling element are as follows:

2.3. Rub-impact fault

As shown in Fig. 3, the rub-impact force can be decomposed into a radial force $F_N$ and a tangential force $F_T$:

where $e={\left(y_{d2}^2+z_{d2}^2\right)}^{\frac{1}{2}}$, $\sigma$ is the radial clearance between the rotor and the stator, $k_r$ is the radial stiffness coefficient of the stator wall, and $f$ is the radial friction coefficient between the rotor and the stator.

Fig. 3The schematic of rub-impact forces

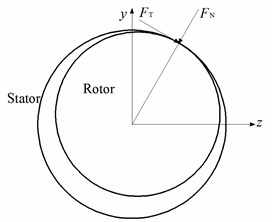
Then the rub-impact forces in the $y$ and $z$ directions can be given as:

2.4. Equations of motion

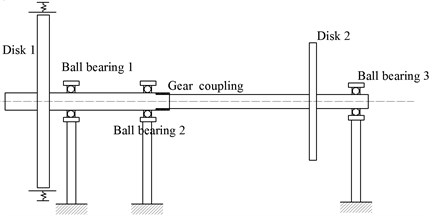
In this study, the rotor system (shown in Fig. 4) consists of two shafts, two disks, three ball bearings and one gear coupling. The rotor is supported in a m pressure is Disk 1 is mounted on the left end of Shaft 1 which is supported by Ball bearings 1 and 2, and Disk 2 is associated with Shaft 2 which is supported by Ball bearing 3 at the right end. The two shafts are connected by the gear coupling.

Fig. 4The model of the rotor-bearing-SFD system

Two assumptions are made as below:

1) The deformations of the journals, the disks, the gear coupling, and the ball bearings are ignored. So, the rotor system is dispersed into 11 lumped mass points connected by mass less shaft sections with axial stiffness;

2) The displacements of the rotor in the axial and torsional directions are negligible so that each mass point has four degrees of freedom including two translations in the lateral and vertical directions and two rotations about the lateral and vertical directions.

The equations of motion of the rotor system are derived as:

where $M_{d1}$ and $M_{d2}$ are the masses of Disk 1 and Disk 2, $M_{r1}$ to $M_{r6}$ are the masses of shaft sections, $C_d$ and $C_b$ are the viscous damping factors of disks and ball bearings, $K_r$ is the stiffness of shaft sections, $F_{P,y}$ and $F_{P,z}$ are the rub-impact forces in the lateral and vertical directions, $F_{b,y}$ and $F_{b,z}$ are the supported forces of ball bearings in the lateral and vertical directions, $F_{m,y}$ and $F_{m,z}$ are the misalignment forces in the lateral and vertical directions, $F_{g,y}$ and $F_{g,z}$ are the meshing forces in the lateral and vertical directions, and $e_{d1}$ and $e_{d2}$ are the eccentricities of Disk1 and Disk 2.

2.5. Numerical method

In this paper, equations of motion are solved by the fourth order Runge-Kutta method, and the time step in the iterative procedure is set as $∆n=$ 1×10^-5 s. The time varying data corresponding to the first 500 periods generated by numerical integration are deliberately excluded in order to discard the transient solutions. The parameters used are listed in Table 1.

2.6. Time-frequency method

Due to the nonlinearity of the system response and the frequency overlap of fault characteristic, traditional features obtained from bifurcation diagram, Pointcaré map and frequency spectrum are not enough for analyzing the faulty rotor system. In this paper, the time-frequency method is employed to dig out more fault information that hidden from time and frequency domains. To this end a wavelet packet decomposition (WPD) improved EMD technique is applied to solving the problem [22]. Although a vibration signal can be decomposed into several IMFs by EMD, some high-frequency small-amplitude harmonics cannot be separated from one modulated IMF. So, the WPD is used to further decompose an IMF into narrow bands. In this way, some discontinuous high frequency contents can be found to illustrate the rub-impact fault. The time-frequency analysis can be operated in four steps:

1) Decompose the vibration signal by EMD method;

2) Further decompose the obtained IMFs using WPD technique and reform the WP coefficients;

3) Choose reformed IMFs that of high concerns as the first IMFs according to the node energy and the correlation between the reformed and original IMFs, and add other IMFs into the residual;

4) Apply Hilbert transform to the new-generated IMFs to obtain the time-frequency distribution of the vibration signal.

3.1. Ball bearing model

To validate the ball bearing model developed in this paper, the calculation results are compared with the results in [25]. The comparison is conducted using the information in frequency domain. Fig. 5(a) shows the results from [25] and Fig. 5(b) is the results from the model.

From both results, it is found that when the speed is far from the critical speeds the motion of the rotor mainly represents at the ball passage frequency and relevant harmonic components. The amplitude of vibration at the VC frequency is far higher than the following harmonics and decreases with increasing VC frequencies. Although the rotor speed is different, the vibration amplitude distribution along the frequency range in this paper is exactly in the same pattern as Ref [25], and both results show the motions are periodic. As a conclusion, the ball bearing model developed in this paper is validated.

3.2. Gear coupling model

In order to verify the misalignment model of the gear coupling, the simulation results of the proposed model are compared with the results of [7]. In the simulation, the vibration displacements in the $z$ and $y$ directions are both 0.001 mm, the static misalignment changes from 0 to 0.2 mm, and the deformation angle of gear tooth is 0°. The meshing forces in the $y$ and $z$ directions are shown in Fig. 6. From the comparison, it is found that the two components of meshing force of the proposed model are in the same pattern as the results of [7]. The difference in the amplitude of meshing force is because the transmitted torque is much smaller than that in the reference due to the rotor structure. When the misalignment is zero, the meshing forces in the two directions are the same. With increasing misalignment, the magnitudes of meshing forces in the two directions begin to increase sharply within the misalignment range from 0 to 1×10^‒4 m. As the misalignment further increases, the two components of meshing force increase very slow and reach stable levels until the end. Obviously, the model developed in this paper is able to reflect the dynamic behavior of gear coupling correctly.

Fig. 5Rotor responses in the x direction: a) in this paper, b) in [25]

a)

b)

Fig. 6Meshing forces under different misalignments: a) in this paper, b) in [7]

a)

b)

3.3. Rotor system model

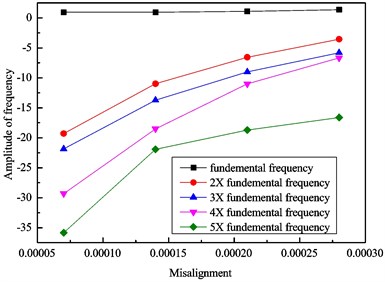
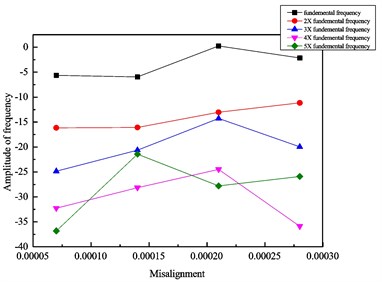
To examine the rotor model, a group of experimental results [12] under different misalignments are used. The comparison between the simulation and the experiments are given in Table 2 and Fig. 7.

Fig. 7Vibration amplitudes of: a) simulation, b) experiment with increasing misalignment

a)

b)

As the misalignment changes, both simulation and experimental amplitudes varies obviously. For the simulation, the amplitudes at all frequencies increase with increasing misalignment. For the experiment, the amplitudes at the fundamental frequency increases monotonously with increasing misalignment, while the amplitudes at other harmonic frequencies increase first then decrease at the end. The reason of this different trend may be the increase of misalignment in the gear coupling leads to a misalignment between the drive motor and the rotor which can bring unpredictable effect on the vibration of rotor system. This conclusion can be found in [26] as well. So, the mathematical model of the two-shaft rotor-bearing system with a misaligned gear coupling can be validated.

4.1. Rub-impact analysis under misalignments

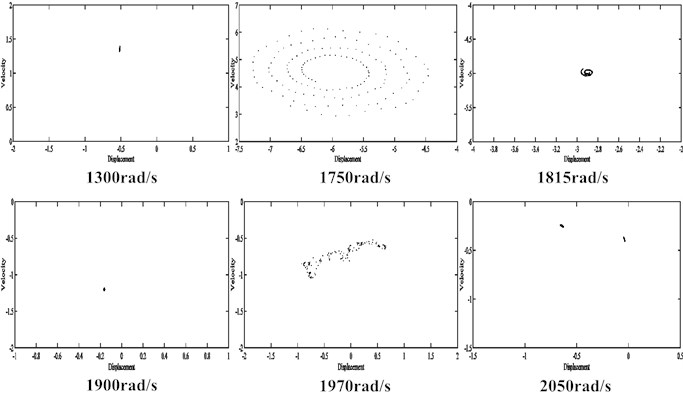
For the rotor system under rub-impact fault but without misalignment, the bifurcation diagram and Pointcaré maps are shown in Fig. 8 and Fig. 9 respectively. The motion of the rotor system is periodic in the rotating speed range of 1000 rad/s to 1650 rad/s and becomes quasi-periodic in the range of 1650 rad/s to 1800 rad/s. Two following jump points appear at 1810 rad/s and 1815 rad/s. Then the motion returns to periodic until 1930 rad/s and goes into quasi-periodic again from 1935 rad/s to 2005 rad/s. Between 2005 rad/s and 2200 rad/s, the motion alternates between period-one and period-two. After that, the motion of the rotor loses its regularity and falls into quasi-period.

Fig. 8Bifurcation diagram of the rotor system under rub-impact fault without misalignment

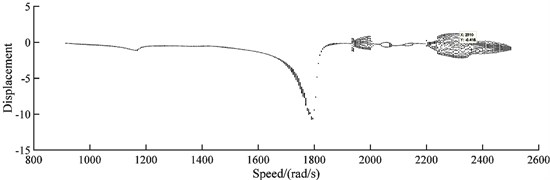
Fig. 9Pointcaré maps of the rotor system under rub-impact fault without misalignment

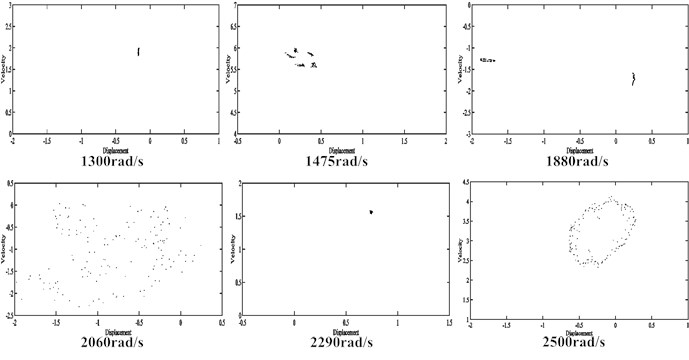
Under 1×10^‒5 m misalignment, the bifurcation diagram of the rub-impact rotor system is shown in Fig. 10 and the corresponding Pointcaré maps are shown in Fig. 11. The motion of the rotor is period-one from 900 rad/s to 1450 rad/s. In the range of 1450 rad/s and 1800 rad/s, the motion of the rotor is quasi-period and jumps at 1805 rad/s, 1810 rad/s, 1815 rad/s and so on. From the last jump point to 2270 rad/s, the motion of the rotor is unstable and goes into chaos. Then the motion becomes periodic from 2275 rad/s to 2345 rad/s and finally returns to quasi-periodic.

Fig. 10Bifurcation diagrams of the rub-impact rotor system with 1×10‒5m misalignment

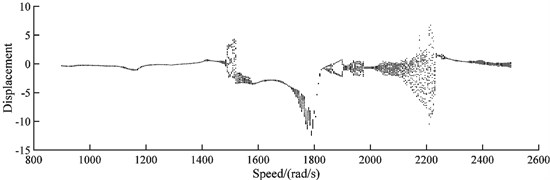
Fig. 11Pointcaré maps of the rub-impact rotor system with 1×10‒5 m misalignment

When the misalignment is increased to 1.4×10^‒1 m, the bifurcation diagram of the rub-impact rotor system is shown in Fig. 12 and the corresponding Pointcaré maps are shown in Fig. 13. The dynamic orbit shows period-one motion when the rotating speed is below 1375 rad/s. As the rotor speed increases to 1590 rad/s, the motion of rotor loses its stability and falls into chaos. After that the motion returns to period-one from 1595 rad/s to 1645 rad/s and goes into quasi-period from 1650 rad/s to 1805 rad/s. After a series jump points, the motion of rotor goes back to period-one in a short range of 1810 rad/s to 1840 rad/s, becomes quasi-period from 1845 rad/s to 2240 rad/s, and then falls into chaos. At the end, the system stability improves but the motion of rotor is still in quasi-period.

Fig. 12Bifurcation diagrams of the rub-impact rotor system with 1.4×10‒4 m misalignment

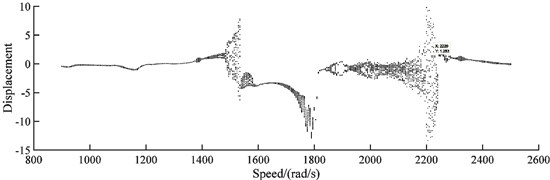
It can be concluded the rub-impact rotor system is always stable at lower speed regardless misalignment. But increasing misalignment can bring the motion of rotor into quasi-period earlier and enlarge the speed range of quasi-period/chaos motion. In other words, the stability of rotor system decreases with increasing misalignment. However, the motions of rotor are unusual that returns to periodic from quasi-periodic in some high-speed ranges, which is further discussed in the next section.

Fig. 13Pointcaré maps of the rub-impact rotor system with 1.4×10‒4 m misalignment

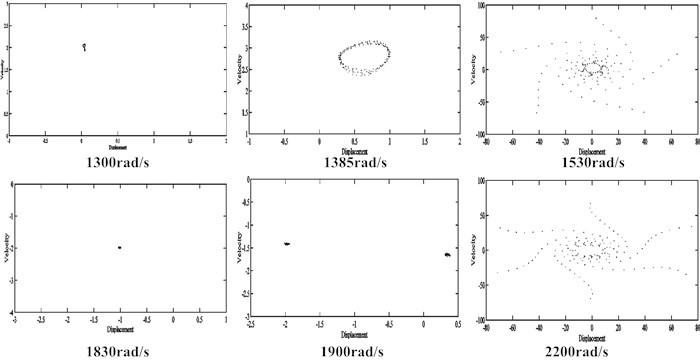
4.2. Effect of misalignment on rotor dynamics

Fig. 14 shows the bifurcation diagram of the rub-impact rotor system with varies of misalignments under 1500 rad/s. It can be found that the dynamic orbit shows period-one with increasing misalignment from 0 to 3×10^‒5 m. In this misalignment range, the rub-impact force is periodic and vibration amplitudes only can be found at fundamental and 2× fundamental frequencies in the spectrum diagram. With increasing misalignment, the peak rub-impact force increases from 1000 N to 6757 N, the variation of rub-impact force is irregular, the motion of rotor system is more unstable, and vibration at some low frequencies can be found around the fundamental frequency.

Fig. 14Bifurcation diagram of the rub-impact rotor with different misalignments under 1500 rad/s

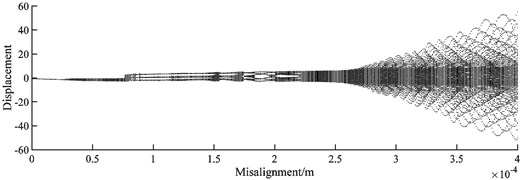
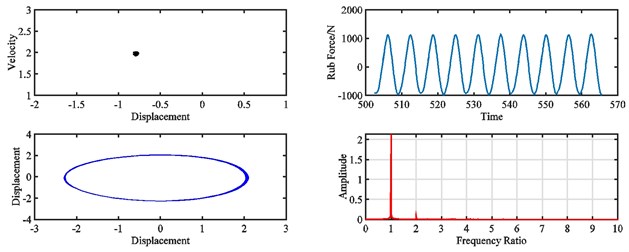
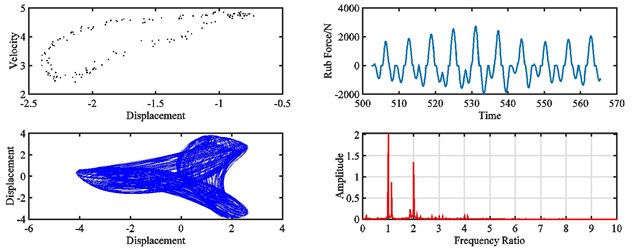
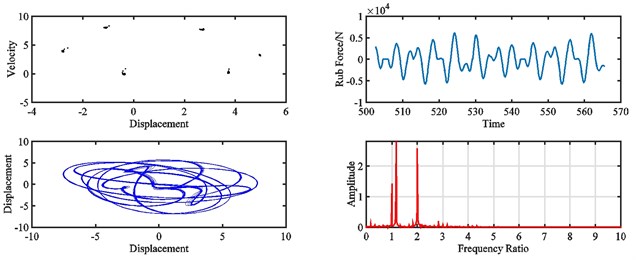
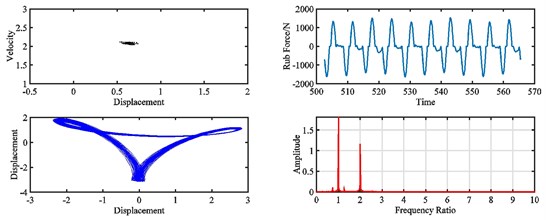
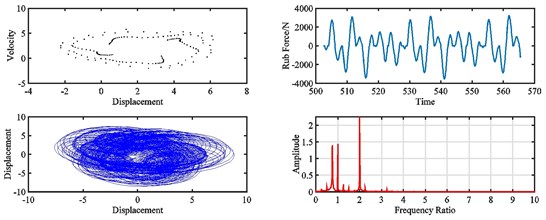
Fig. 16 and Fig. 17 show the dynamic responses of the rotor system with varies of misalignment at 2320 rad/s. It can be found that the motion of the rotor is quasi-periodic when the misalignment develops from 0 to 7.5×10^‒5 m.

Without misalignment, the rub-impact force is irregular, and the peak amplitude is 1960 N, and low frequency vibration around the fundamental frequency can be found on the spectrum. As the misalignment grows from 7.5×10^‒5 m to 9.3×10^‒5 m, the motion of rotor goes into period-one, the peak amplitude of rub-impact force reduces to 1250 N, the force time history becomes more regular, and vibration around the fundamental frequency mitigates a lot. With further increased misalignment, the motion of rotor returns to quasi-period, the rub-impact force becomes irregular again in time domain, the amplitude of rub-impact force is almost doubled, and a considerable vibration peak appears at low frequency.

Fig. 15Pointcaré map, rub force, rotor orbit and spectrum diagram of rub-impact rotor at 1500 rad/s under misalignment of: a) 0 m, b) 5×10‒5 m, c) 1.85×10‒4 m, d) 3.3×10‒4 m

a)

b)

c)

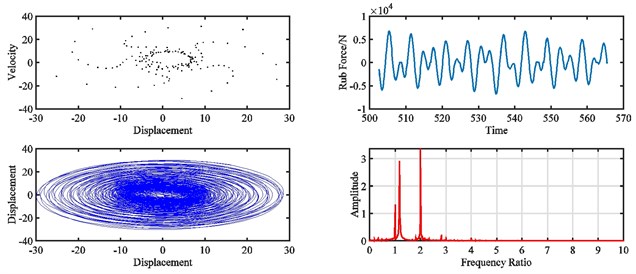
d)

Fig. 16Bifurcation diagram of the rotor system with different misalignments at 2320 rad/s

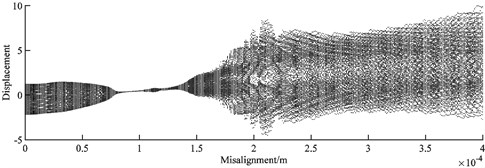
Fig. 17Pointcaré map, rub force, rotor orbit and spectrum diagram of rub-impact rotor at 2320 rad/s under misalignment of: a) 0 m, b) 9×10‒5 m, c) 1.2×10‒4 m, d) 2.2×10‒4 m

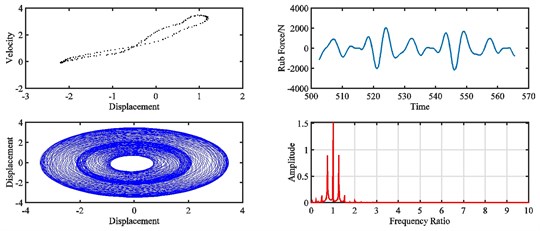
a)

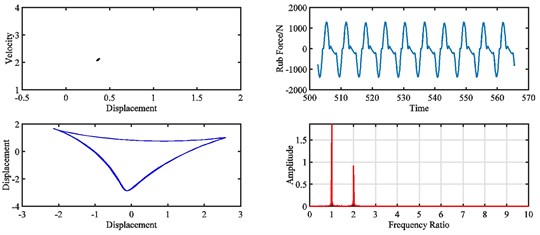
b)

c)

d)

4.3. Time-frequency analysis

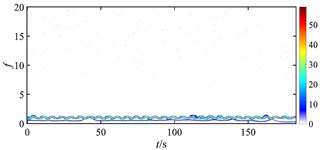
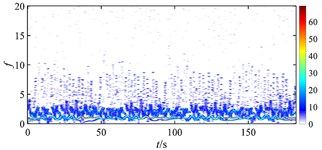
Fig. 18 gives the time-frequency maps of the rub-impact force of rotor under different misalignments. Without misalignment (as Fig. 18(a)), the rub-impact force is nearly continuous with few weak intermittent components at high frequency, and the energy distributes around the fundamental frequency evenly. When the misalignment appears at a relatively low level (as Fig. 18(b)), numbers of intermittent components can be found at low frequency range, the energy distribution is messy, and the magnitude of energy starts to increase. As the misalignment further develops (as Fig. 18(c), (d) and (f)), the intermittent components reduce a lot, the energy distribution of the signal becomes more regular, and the magnitude of energy stops increasing. It can be seen that the occurrence of misalignment has the biggest impact on the rub-impact force of rotor system, which is greatly deteriorated due to a small increment of misalignment from nothing to a very low level. In other words, the stability of rub-impact rotor decreases a lot at the moment that misalignment starts, but stops to further decrease with further increasing misalignment.

Fig. 18Time-frequency maps of rub-impact force at 1500 rad/s under misalignment of: a) 0 m, b) 5×10‒5 m, c) 1.85×10‒4 m, d) 2×10‒4 m, e) 2.4×10‒4 m, f) 3.3×10‒3 m

a)

b)

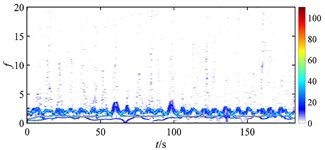
c)

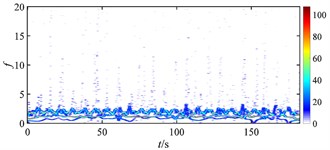
d)

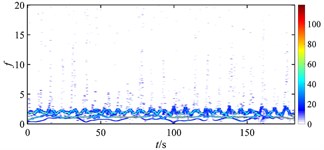
e)

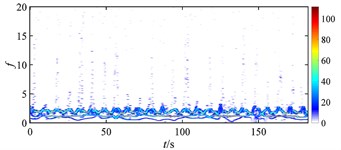
f)

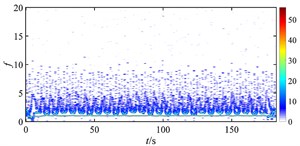
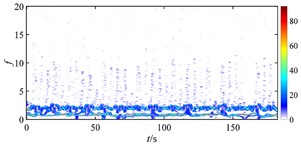
Fig. 19 shows the time-frequency maps of the rub-impact force of rotor under different misalignments at higher rotating speed. When there is no misalignment, it is found that the energy distribution of rub-impact force is not as evenly as that at lower speed (shown in Fig. 18 (a)) due to some low frequency components. When the misalignment is 5×10^‒5 m, lots of intermittent components appear at low frequencies which make the energy distribution more irregular, but the magnitude of energy decreases. As the misalignment increases to 9×10^‒5 m, the energy of rub-impact force is focused on the fundamental frequency, and more intermittent disturbances spread in low frequency range. But some high frequency components start to show periodic distribution. With increasing misalignment, the magnitude of energy increases, and the distribution is more irregular. Combined with Fig. 17, it can find that the motion of rotor turns from quasi-period to period-one due to the increase of misalignment, but this state is unstable because of the periodic intermittent high frequency rub-impact component. With further development of misalignment, the rub-impact force becomes more irregular and results in chaos of the rotor system.

Fig. 19Time-frequency maps of rub-impact force at 1940 rad/s under misalignment of: a) 0 m, b) 5×10‒5 m, c) 9×10‒5 m, d) 1.2×10‒4 m, e) 2.2×10‒4 m, f) 3×10‒4 m

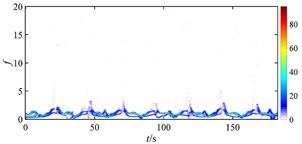
a)

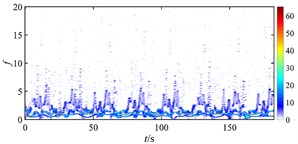
b)

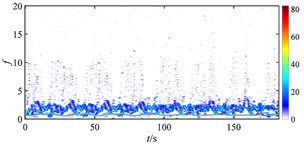
c)

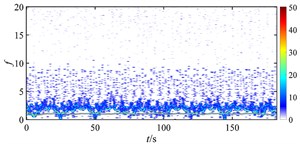
d)

e)

f)