Application of deterministic resampling particle filter to fatigue prognosis

2.1. Fatigue crack growth prognosis based on particle filter

In the PF theory, a state space model, which consists of a state equation and a measurement equation, needs to be defined. The state equation describes the state evolution representing a hidden Markov process of order one, as shown in Eq. (1). The measurement equation governs the relationship between the measurement value and the system state, as shown in Eq. (2):

where $k$ is the discrete time index, ${\mathbf{x}}_k$ is the system state, $f(\cdot )$ is a nonlinear model representing the state evolution from time $k-1$ to time $k$, ${\theta }_{k-1}$ is the model parameter vector, ${\omega }_{k-1}$ is a random variable representing the state noise; $y_k$ is the state measurement of the state ${\mathbf{x}}_k$, $g(\cdot )$ represents the relationship between the measurement $y_k$ and the state ${\mathbf{x}}_k$, $\nu$ is a random variable denoting representing the measurement noise.

For solving fatigue crack growth problem, the state equation can be determined by a physic-based crack growth model. The Paris’ law [26] has been widely used, giving the crack growth rate as Eq. (3):

where $a$ is the crack length, $N$ is the number of loading cycles, $C$ and $m$ are the material constants, $\mathrm{\Delta }K$ is the stress intensity factor (SIF) range acting as the crack growth force, which is expressed as Eq. (4):

where $\mathrm{\Delta }\sigma$ is the stress amplitude, $F$ is the geometric coeffecient.

Eq. (3) can be expressed in a discrete form to represent the crack evolution from time $k-\text{1}$ to time $k$ as expressed in Eq. (5):

where $\mathrm{\Delta }N$ is the discrete step of loading cycles, the product $C(\mathrm{\Delta }K{)}^m\mathrm{\Delta }N$ gives the crack length increment for each time step. The random variable $\omega$ follows the Gaussian distribution $N(-{\sigma }_{\omega }^2/\text{2}$, ${\sigma }_{\omega }^2)$, and the term $\mathrm{e}\mathrm{x}\mathrm{p}\left(\omega \right)$ that is nonnegative is incorporated for representing uncertainties during the fatigue crack growth [27]. Thus, $\mathrm{e}\mathrm{x}\mathrm{p}\left(\omega \right)$ is lognormally distributed. The mean value of $\omega$ is selected as $-{\sigma }_{\omega }^2/\text{2}$ such that the expectation of $\mathrm{e}\mathrm{x}\mathrm{p}\left(\omega \right)$ is equal to 1 [15].

To express the uncertainty between different structures, the parameter $C$ is considered as a random variable and the material parameter $m$ is adopted as a constant. Thus, the PF state vector is represented as ${\mathbf{x}}_k=[a_k,C_k]$. As a result, the state equation is expressed as Eq. (6):

On the other aspect, the measurement function is defined to express the relationship between the measurement and the crack length. By using the SHM technologies, the crack length can be monitored on-line. Among SHM methods, the active guided wave based method is one of the most appealing and effective methods, which have the advantages including the sensitivity to a small damage as well as the ability of region monitoring [28, 29]. The quantity extracted from guided wave signals called as the damage index is usually applied to quantify the crack length. Thus, the measurement equation can be denoted as Eq. (7):

where the random variable $\nu$ follows the Gaussian distribution $N$($0$, ${\sigma }_v^2$), denoting that the damage index is affected by zero mean Gaussian noise, $g(\cdot )$ is a one-to-one mapping between the crack length and the damage index dominated by models such as polynomial or artificial neural network.

At the current time $k$, the PF objective is to calculate the posterior PDF $p\left({\mathbf{x}}_k\right|y_{1:k})$ of the system state, conditioned on the measurements $y_{1:k}=$ {$y_1$, $y_2$, ..., $y_k$}. This posterior PDF can be evaluated with the well-known iterative prediction and updating steps according to the Chapman-Kolmogorov equation and the Bayes’ rule [30]. However, this iterative procedure does not have analytical solutions in most cases. The PF deals with it by using the Monte Carlo method: the posterior PDF $p\left({\mathbf{x}}_k\left|y_{1:k}\right.\right)$ is approximated by a set of random samples $\{{\mathbf{x}}_k^{\left(i\right)}$, $i=$ 1, ..., $N_s\}$ called as “particles” with associated weights $\{{\tilde{w}}_k^{\left(i\right)}$, $i=$ 1, ..., $N_s\}$, shown in Eq. (8):

where $N_s$ is the number of particles and ${\mathbf{x}}_k^{\left(i\right)}$ is sampled from a PDF called as the importance density. $\delta (\cdot )$ is the Dirac delta function. In the basic PF, the weight ${\tilde{w}}_k^{\left(i\right)}$ is calculated through the likelihood value $p\left(y_k\right|{\mathbf{x}}_k^{\left(i\right)})$ of each particle, as shown in Eq. (9):

As the measurement equation defined in Eq. (7), the particle weight updating is performed as Eq. (10):

After that, the weight normalization as Eq. (11) is performed to ensure the sum of weights being equal to 1:

As a result, the posterior estimation of the system estimate can be evaluated as the weighted summation of the particles:

Based on the posterior PDF of the state $p\left({\mathbf{x}}_k\left|y_{1:k}\right.\right)$, a prognosis of the future state evolution is performed by projecting the particles in the posterior PDF in time up to the future as follows:

where $k+d$ is the future time of interest.

2.2. Deterministic resampling

In Eq. (11), the variance of particle weights $\{{\tilde{w}}_k^{\left(i\right)},i=1,...,N_s\}$ can only increase overtime [30], so that the particle weight will concentrate on a few particles and most particles will have negligible weights. The basic particle filter adopts the multinomial resampling algorithm, which draws a new particle set from $\{{\mathbf{x}}_k^{\left(i\right)}$, $i=$ 1, ..., $N_s\}$ with the probability proportional to the normalized weight $\{{\tilde{w}}_k^{\left(i\right)}$, $i=$ 1, ..., $N_s\}$. If the weight ${\tilde{w}}_k^{\left(i\right)}$ of the $i$th particle is large, this particle is duplicated as several particles, otherwise this particle will not be contained in the new particle set. The size of the new particle set keeps being equal to $N_s$, and the total particle weight is set to $\text{1}/N_s$. However, this procedure brings the side effect of sample impoverishment problem that most particles are replications of the same particle after several iterations. To overcome the sample impoverishment problem, the deterministic resampling particle filter [25] is adopted in this paper, where the deterministic resampling procedure is conducted after the weight normalization.

The deterministic resampling procedure generates particles from two parts: (1) copy particles; (2) support particles.

1) Copy particles:

For the $i$th particle ${\mathbf{x}}_k^{\left(i\right)}$, it is duplicated for $n_i$ times, where $n_i$ is the integer part of the product $N_s\cdot {\tilde{w}}_k^{\left(i\right)}$, as shown in Eq. (15):

where the symbol $⌊\cdot ⌋$ means the integer part. For all $N_s$ particles, total $N_{cp}={\sum }_{i=1}^{N_s}{n}_i$ copy particles are obtained, what is denoted as $\left\{\right({\mathbf{x}}_k^{\left(j\right)}{)}_{cp}{\}}_{j=1}^{N_{cp}}$.

After that, the residual weight of each particle is evaluated as Eq. (16):

2) Support particles:

Instead of uncensored discarding particles that have small weights, the state space of particles is partitioned into variable-size countable units considering the residual weight of the particle and their spatial distribution. Assuming the particle set with residue weights $\left\{\right({\mathbf{x}}_k^{\left(i\right)},{\widehat{w}}_k^{\left(i\right)}){\}}_{i=1}^{N_s}$ is divided into $N_g$ spatial grids. The $p$th grid is denoted as Eq. (17):

where the subscript $p$ denotes the index of partition grid $p=$ 1, 2,…, $N_g$, $d_p$ is the number of particles contained in the $p$th grid and is defined as the particle density. If a grid is without any particles, it is called an empty grid.

The partition of the spatial distribution is initialized with a starting grid size ${\mathbf{L}}_{start}$, which does not have more dimensions than the state space. All particles are first partitioned into grids of size ${\mathbf{L}}_{start}$. Then the particle density of each nonempty grid is detected: if it is more than a predefined threshold $\alpha$, the grid is subdivided into half size in all dimensions; otherwise, the grid is considered as an independent one. This detection and partition procedure is repeated until the particle density of all grids is below $\alpha$ or the grid size is lower than the threshold bound $L_{\mathrm{m}\mathrm{i}\mathrm{n}}$. Here, $L_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is a pre-set threshold, which prevents grids from being divided into portions of too small size [25]. Fig. 1 shows a partition when the state $\mathbf{x}$ has two dimensions. Particles are located in several grids according to their state values and residue weights.

Fig. 1Illustration of spatial grids of deterministic resampling

After the spatial partition is completed, particles are sampled from these grids, called as support particles. Assuming the total $N_o$ non-empty grids are obtained, a support particle is obtained for the $p$th nonempty grid, $p=$ 1, 2, 3, ..., $N_o$, as shown in Eq. (18):

where symbol $\Rightarrow$ denotes the summing up. The weighted summation of the particles in the partition grid is deemed as the newly resampled particle $({\mathbf{x}}_k^p{)}_{sp}$. The summation of the particle weights $(w_k^p{)}_{sp}$ in this partition grid is adopted as a new weight of the resampled particle. Through this procedure, the deterministic resampling preserves low-weight particles during resampling for possible usages in the future [25].

The weight of the copy particle $({\mathbf{x}}_k^{\left(j\right)}{)}_{cp}$, $j=$ 1, 2, 3, ..., $N_{cp}$, is specified as the equal division of the complement of the support particle weights, as expressed in Eq. (19):

The resampled particle set consists of the copy particles $\left\{\right({\mathbf{x}}_k^{\left(j\right)}{)}_{cp}{\}}_{j=1}^{N_{cp}}$ and support particles $\left\{\right({\mathbf{x}}_k^p{)}_{sp}{\}}_{p=1}^{N_o}$. It should be noted that the particle number $N_s=N_{cp}+N_o$ changes along with the iteration, which is no longer a fixed number.

2.3. Implementation of proposed fatigue crack growth prognosis method

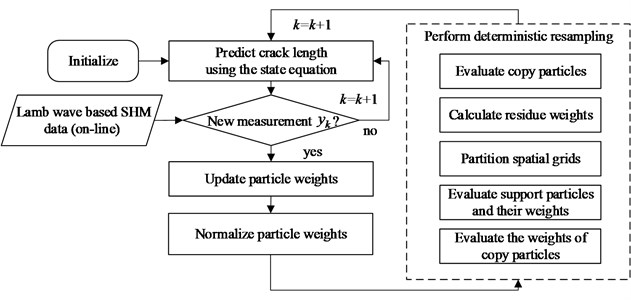
Fig. 2 shows the framework of the proposed fatigue crack growth method. While the structure is under service and monitored with the active Lamb wave based SHM, the measurement of the crack length is sequentially obtained and inputted into the DRPF. Once a new measurement is available, it is used to update particle weights. Thus, the posterior PDF is calculated and is the basis of the crack growth prognosis. After that, deterministic resampling is conducted to resample particles from the spatial distribution of particles, and the newly obtained particles are transferred to the next time step.

Fig. 2Framework of fatigue crack growth prognosis based on DRPF

3.1. Experimental setup

Five edge-crack specimens are manufactured using a LY12 aluminum plate of 2 mm thickness, as illustrated in Fig. 3, which geometry and sensor layout are shown in Fig. 4. These specimens are labeled as T1, T2, T3, T4 and T5. A notch of length is machined at the specimen edge to initiate the crack and control the direction of crack growth. The notch length is selected as 50 mm to accelerate the fatigue tests. Two columns of holes at each end of the specimen are used to assemble the fixture with bolts.

Fig. 3Edge crack specimen

Fig. 4Geometry and PZT layout

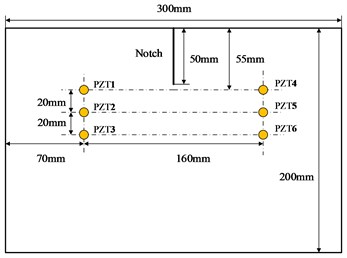
During the fatigue test, the active Lamb wave based SHM is employed to monitor the crack growth in real time. Encapsulated piezoelectric transducers called as peizoelectric transducer (PZT) layers [31] are adhered to the surface of specimen for exciting and acquiring guided wave signals. Totally six PZTs are attached on the surface of each specimen. These PZTs are numbered as PZT1, PZT2, PZT3, PZT4, PZT5, PZT6 respectively, where PZT1, PZT2, PZT3 are used as the actuators, and the others are employed as the sensors. The signal transmitting path, where the signal is excited with PZT1 and sensed with PZT4, is denoted as Channel 1-4. Totally three Channels are employed: Channel 1-4, Channel 2-5, and Channel 3-6, which have different distances from the crack tip.

Fig. 5 illustrates the experimental setup of the fatigue test. The MTS electro-hydraulic servo material test system is used for applying the fatigue load. The specimen is clamped with the fixture at the both ends. The multi-channel PZT array scanning system developed by the authors’ group [32] is adopted for signal actuating and acquiring. Before fatigue tests, a tensile test is performed with T1 specimen to determine the fracture load of the cracked specimen. As a result, the fracture load of this specimen is 56 kN. Thus, the fatigue load of T2-T5 specimens is chosen as the sinusoid load of the peak value $P_{\mathrm{m}\mathrm{a}\mathrm{x}}=$ 17 kN, stress ratio $R=P_{\mathrm{m}\mathrm{i}\mathrm{n}}/P_{\mathrm{m}\mathrm{a}\mathrm{x}}=$ 0.1 and 10 Hz load frequency. The experimental crack length is observed at 5mm interval, while the Lamb wave based crack monitoring is performed. The 5-cycle Hanning-windowed sine burst signal with the center frequency of 250 kHz and ±70 V amplitude is used as the excitation signal, and the response Lamb wave signals are acquired from three channels with the 10 MHz sample rate.

Fig. 5Experimental setup

3.2. Experimental results

Fig. 6 shows the fatigue crack growth trajectories of T2-T5 specimens observed at 5 mm interval. It can be found, although the specimen and fatigue loads are identical, these fatigue crack growth trajectories are diverse. This is because the fatigue crack growth process is a stochastic process, which is affected by numerous uncertainties derived from sources such as the intrinsic material property, specimen machining and assembling error [27]. Thus, crack growth prognosis made by a deterministic physical model may cause a large error.

Fig. 6Experimental crack lengths versus loading cycles of T2-T5 specimens

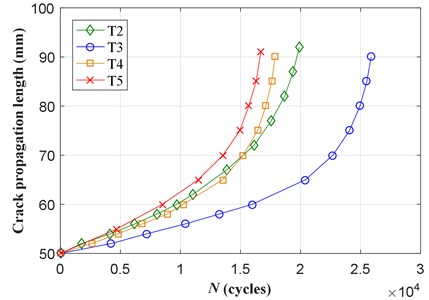
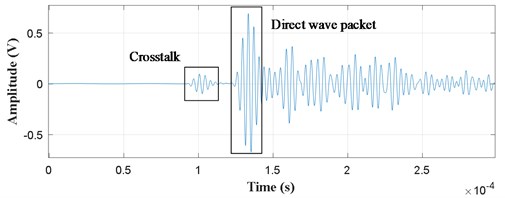
Fig. 7 illustrates a typical Lamb wave signal acquired from the Channel 2-5 with PZTs. The crosstalk is caused by the excitation signal which is a 5-cycle Hanning-windowed sine burst. The direct wave packet is the first wave packet transmitted from the actuator to the sensor, thus it carries the most important information of the crack growth process. The amplitude and phase of the direct wave packet changes with the increase of the crack length. These changes can be used to represent the crack growth. A quantity called as the damage index is usually employed to quantify the changes between changed signals and the signal collected at the pristine state called as the baseline signal. The normalization correlation moment (NCM) damage index [33] is adopted in this paper, which is expressed as Eq. (20):

where $y$ is the damage index, $r_{pq}\left(\tau \right)$ is the cross-correlation function of the baseline signal $p\left(t\right)$ that is collected at the pristine state and the signal $q\left(t\right)$ collected during the crack growth, $r_{pp}\left(\tau \right)$ is the autocorrelation function of the signal $p\left(t\right)$, $T$ is the signal length, $e$ is the order of the statistical moment that is arbitrary and not limited to integers.

Fig. 7Typical lamb wave signal acquired from channel 2-5

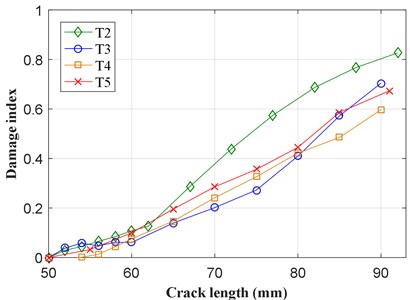
To calculate the NCM damage index, the direct wave packet is used instead of the whole signal. The baseline signal is collected when each specimen is clamped, and the crack does not start to grow. As shown in Fig. 4, there are three channels, the damage index calculated is different from other channels because the positions of these channels are different from each other. After comparison, damage indices extracted from Channel 2-5 represent good correlation with crack lengths of T2-T5 specimens, as shown in Fig. 8, which are calculated with the statistical moment $e=$ 1.

Fig. 8Experimental crack length versus NCM damage index

3.3. Validation of the proposed DRPF based on-line fatigue crack growth prognosis

To validate the method, the last T5 specimen is used as the target structure to validate the proposed method. Thus, the fatigue test data of T2-T4 specimens are employed as the database to establish the state space model of edge-crack specimen.

3.3.1. State space model of edge-crack specimen

In the state equation defined for fatigue crack growth, as shown in Eq. (5), the SIF range $\mathrm{\Delta }K$ of the edge-crack plate can be calculated through Eq. (21) referring to the SIF handbook [34]:

21

$\mathrm{\Delta }K=\mathrm{\Delta }\sigma \sqrt{\pi a}F\left(\frac{a}{b}\right),$

where $\mathrm{\Delta }\sigma$ is the nominal stress amplitude, $a$ is the length of the edge crack, $\text{2}b$ is the width of the edge-crack plate, $F$ is the geometric correction factor which is the function of the ratio $a/b$. This correction factor is expressed as follows:

22

$F\left(\frac{a}{b}\right)=\sqrt{\frac{2b}{\pi a}\mathrm{t}\mathrm{a}\mathrm{n}\frac{\pi a}{2b}}\cdot \frac{0.752+2.02\frac{a}{b}+0.37{\left(1-\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi a}{2b}\right)}^3}{\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi a}{2b}}.$

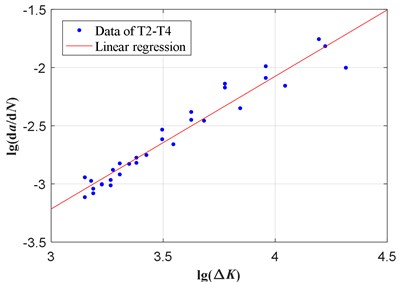
Usually, the parameters $C$ and $m$ in the Paris’ law is obtained with fatigue test data of the same specimens. In this paper, the crack growth data of T2-T4 specimens is used to fit these parameters to describe the prior knowledge of fatigue crack growth of edge crack specimen. The logarithm transformation of the Paris’ law gives Eq. (23):

23

$\mathrm{l}\mathrm{g}\left(\frac{da}{dN}\right)=\mathrm{l}\mathrm{g}\left(C\right)+m\mathrm{l}\mathrm{g}\left(\mathrm{\Delta }K\right),$

where $\mathrm{l}\mathrm{g}\left(C\right)$ and $m$ are the intercept and slope of the linear relationship between $\mathrm{l}\mathrm{g}\left(\mathrm{\Delta }K\right)$ and the crack growth rate $\mathrm{l}\mathrm{g}(da/dN)$. The data points of the crack growth rate can be approximated by applying the commonly used secant method [35]. Fig. 9 illustrates the data points of T2-T4 specimens. Through linear regression, the fitted parameters are obtained as $m=$ 3.819 and $\mathrm{l}\mathrm{g}\left(C\right)=$ –13.624.

To express the uncertainty between different structures, the parameter $C$ is considered as a random variable, and the material parameter $m$ in Eq. (6) is adopted as a constant. The uncertainty of the material parameter $C$ is considered in the crack growth model. The prior distribution of the parameter $C$ is adopted as $\mathrm{l}\mathrm{g}\left(C\right)~N$(–13.624, ${\sigma }_C^2=$ 0.3²), in which ${\sigma }_C^2=$ 0.3² is adopted so that it is efficient to represent the dispersion of the crack growth regulated by the Paris’ law.

Fig. 9Linear regression for Paris model parameters

In the measurement equation, shown in Eq. (17), the measurement mapping $g(\cdot )$ represents the relationship between the crack length and the measured crack length. With the experimental results of T2-T4 specimens shown in Fig. 8, this mapping can be obtained by polynomial fitting as Eq. (24):

24

$y=-7.897\times 10^{-6}(a-a_0{)}^3+6.663\times 10^{-4}(a-a_0{)}^2+3.343\times 10^{-3}(a-a_0{)}^{},$

where $a$ is the crack length, $a_0=$ 50 mm is the initial crack length (notch length).

Thus, the measurement equation is expressed as follows:

25

$y_k=-7.897\times 10^{-6}(a_k-a_0{)}^3+6.663\times 10^{-4}(a_k-a_0{)}^2$
$+3.343\times 10^{-3}\left(a_k-a_0\right)+v,$

where $v~N(0,{\sigma }_v^2)$ denotes the measurement uncertainty. The variance ${\sigma }_{\nu }^{}=$ 0.064 is also calculated with the experimental results of T2-T4 specimens by using the maximum likelihood estimation.

3.3.2. Fatigue crack growth prognosis of T5 specimen

T5 specimen is used as the target structure to validate the proposed DRPF based crack growth prognosis method. For the on-line crack growth prognosis of T5 specimen, the DRPF parameter is set as $N_s=$ 50, $\mathrm{\Delta }N=$ 50, and ${\sigma }_{\omega }^2=$ 0.01. The starting grid size ${\mathbf{L}}_{start}=$ [$w_{start}$, $a_{start}$, $C_{start}$] of the state space partition in deterministic resampling is adopted as:

$w_{start}=\frac{\mathrm{m}\mathrm{a}\mathrm{x}\left({\widehat{w}}_{k+1}^i\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left({\widehat{w}}_{k+1}^i\right)}{5},a_{start}=\frac{\mathrm{m}\mathrm{a}\mathrm{x}\left(a_{k+1}^i\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(a_{k+1}^i\right)}{5},$

$C_{start}=\frac{\mathrm{m}\mathrm{a}\mathrm{x}\left(C_{k+1}^i\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(C_{k+1}^i\right)}{5},\alpha =3.$

At the initial time $k=$ 0, $N_s$ random samples $\{C_0^i{\}}_{i=1}^{N_s}$ are drawn from the distribution $\mathrm{l}\mathrm{g}\left(C\right)~N$(–13.624, 0.3²) and assigned to each particle and the particle set is initialized as $\{\left(a_0^{\left(i\right)}=a_0,C_0^{\left(i\right)}\right)\text{,}i=$ 1,...,$N_s\}$. Meanwhile, the weight of each particle is initialized as $\{w_0^{\left(i\right)}=1/N_s$, $i=$ 1,..., $N_s\}$.

During the fatigue test of T5 specimen, guided wave signals are excited and acquired sequentially. The damage index is extracted from these signals as the measurement of the actual crack length, which is employed to calculate the particle weight. Thus, the posterior PDF of the crack length and parameter $C$ is obtained as the approximation with the help of the particles $\left\{\right(a_k^{\left(i\right)},C_k^{\left(i\right)})$, $i=$ 1, ..., $N_s\}$ and associated weights $w_k^{\left(i\right)}$. Based on the posterior PDF, crack growth prognosis is performed. And then the deterministic resampling is conducted according to the spatial distribution of the particles. As mentioned above, the particles are initialized with $\{C_0^i{\}}_{i=1}^{N_s}$. After each resampling procedure, values in $\{C_0^i{\}}_{i=1}^{N_s}$ are duplicated and eliminated for each particle. Thus, the particle diversity can be represented by counting the unique $C$ values of particles. Fig. 10 illustrates the varying number of different particles after resampling processes when new measurements are available. It can be found that the particle impoverishment problem of the basic PF is serious only after several resampling procedures. By contrast, the DRPF maintains a diversity particle set.

Fig. 10Varying number of unique C values after resampling processes

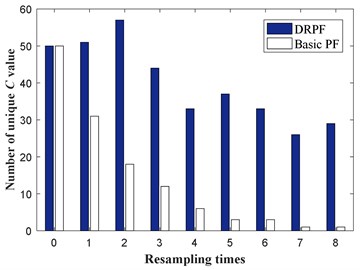
Fig. 11Posterior estimate of the crack length considering all the crack measurements

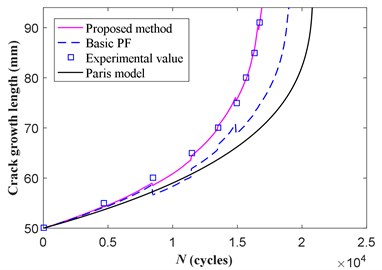
During on-line prognosis, the posterior PDF of the crack length and parameter $C$ is used as the initial conditions for prognostic routines. Fig. 11 illustrates the prognosis results given by the basic PF and DRPF. In this figure, the crack growth trajectory of the Paris model represents the result by using the Paris’ law with the fitted parameter $\mathrm{l}\mathrm{g}\left(C\right)=$ –13.624, $m=$ 3.819, and $a_0=$ 50, $\mathrm{\Delta }N=$ 50, which results in the biggest error. The prognosis result of the basic PF slightly improved by considering the actual crack measurement, however there is still a large error because of particle impoverishment. On the other hand, the DRPF gives quite a good result. The root means square error (RMSE) of the basic PF and DRPF is 1.5 mm and 10.5 mm respectively, showing the effectiveness of the proposed method.