Abstract
Gear has been widely used in the modern industry, and the gear reliability is important to the driving system, which makes the residual fatigue life prediction for a gear crucial. In order to realize the residual fatigue life of the gear accurately, a hybrid approach based on the Paris law and particle filter is proposed in this paper. The Paris law is usually applied to predict the residual fatigue life, and accurate model parameters allow a more realistic prediction. Therefore, a particle filtering model is utilized to assess both model parameters and gear crack size simultaneously. As a data-driven method, particle filter describes the dynamical behavior of model parameters updating and gear crack growth, whereas the Paris law, as a model-based method, characterizes the gear’s crack growth according to the physical properties. The integration of the Paris law and particle filter is proposed as a hybrid approach, which is suitable for nonlinear and non-Gaussian systems, and can update the parameters online and make full use of the prior information. Finally, case studies performed on gear tests indicate that the proposed approach is effective in tracking the degradation of gear and accurately predicts the residual gear fatigue life.
1. Introduction
Gear is one of the key components in a driving system, and it has been widely used in the modern industry. The gear reliability is important to the system safety, and it is necessary to investigate the allowable crack size present in the gear to avoid a sudden system failure [1]. Therefore, it is important to estimate the useful gear fatigue life within the shortest times, that is helpful for monitoring health conditions of machines and estimating whether the machines can accomplish the routine task or not [2].
Currently, machine prediction approaches can roughly be categorized into model-based and data-driven approaches [3]. The Paris law is a widely used model-based prognostic approach, and it has been proven that gear crack-growth rates follow it [4]. In addition, fatigue life prediction models in most literature sources are based on the traditional Paris law and are usually established based on monitoring and estimation of well-known direct damage indicators such as a crack size [5]. Therefore, the fatigue life prediction based on the Paris law has received considerable attention in recent years [6-10], and it has been applied to a range of applications, including axial flow compressors [1], girth gear-pinion assembly [11], ball bearings [2], and interfacial cracked plate [12]. However, it is hard to acquire real-time data of crack lengths and flaw sizes without interrupting the machine operation and model parameters which have an effect on the model behavior are often unknown and need to be identified as a part of the prediction process. In order to realize the fatigue life prediction based on the Paris law, a variety of improved methods are proposed. Dong Xu, et al. [2] proposed two improved Paris models based on the intrinsic mode function (IMF) involving the fault characteristic frequency which has a consistent trend with the diameter of flaws. Yuning Qian, et al. [13] integrated enhanced phase space warping with a Paris crack growth model to propose a multi-time scale approach for bearing defect tracking and residual useful life prediction. Ben Abdessalem, et al [14] predicted the fatigue crack growth by a Markov process associated with deterministic crack laws, which provide a reliable prediction and can be an efficient tool for a safety analysis of structures in a large variety of engineering applications.
The Paris model depends on its parameters for accurate prediction of the fatigue life. Many contributions for the parameter estimation of Paris law have been presented in the published literatures. In most cases, the Paris law parameters can be derived from fracture mechanics tests [15], however, the crack growth in structures depends on many factors, such as the amplitude, stress ratio, or frequency of the load, which are difficult to be estimated correctly. The extended Kalman filter (EKF) is proposed as an estimation method for the parameters identification of Paris law which is used as fatigue-crack-length growth model under loading cycles [16]. However, it is different to realize the parameters when it comes to nonlinear situation. Particle filter is widely used in the engineering, and it is especially suitable for processing the nonlinear and non-Gaussian systems [5, 17, 18]. Hence, we take the particle filtering technique as an inference method inside the dynamic Bayesian network to assess both model parameters and damage states simultaneously.
In this paper, a hybrid approach based on the Paris law and particle filter is proposed to predict the residual gear fatigue life with prior crack growth information, which considers the gear fracture mechanics and makes full use of the prior information to improve the prediction performance. First, the gear degradation process is described by the Paris law. Then, the PF model is proposed as an estimation method for the parameters identification. As a result, the integration of data-driven approach and model-based approach is used for the residual fatigue life prediction, which makes full use of the advantages of two approaches and makes the prediction more accurate.
The rest of this paper is organized as follows. In Section 2, the Paris law and particle filter are introduced separately. In Section 3, the residual fatigue life prediction based on hybrid approach is proposed, and the particle filter is proposed to update the unknown parameters of Paris model. Then, the implementation steps of the hybrid prediction approach are discussed. In Section 4, a test of the gear crack growth is used to prove the proposed method. Finally, the conclusions are drawn in Section 5.
2. Introduction of Paris law and PF model
2.1. Short overview of Paris law
In 1963, Paris, et al [19] proposed the Paris law based on fracture mechanics, which can reflect the failure mechanism of materials and is usually applied as a method to predict fatigue life or residual fatigue life. The stress intensity factor (SIF) plays a key role in the process of the fatigue crack propagation, and a number of tests are carried out to study the influence for crack propagation. It has been found that for the first loading mode the SIF increases along with the increase of the crack depth and for the second loading mode the SIF decreases along with the increase of the crack depth. The crack propagation rate measured was similar with the SIF amplitude variation. Based on the above, the Paris law for the fatigue crack propagation under the constant amplitude loading was proposed:
where represents the crack size, represents the number of stress cycles, is the range of the stress intensity factor, is the stress range, and are the parameters of the Paris law which are usually determined by material constants.
2.2. Particle filter model
The particle filter employs the Monte Carlo simulation of a state dynamic model and Bayesian estimation for estimating the posterior probability density function (PDF) of the state. Therefore, the method is an effective tool for nonlinear and non-Gaussian systems. The state equation and measurement equation of particle filter are expressed as follows [20]:
where is the damage state to be estimated, is the time step index, is a vector of model parameters, is the measurement data, and are process and measurement noise, respectively. and represent the known process and observation functions, respectively.
The probability density function of the update unknown parameters can be obtained based on the following Bayes’ theorem:
where is a set of the unknown parameters, is a vector of monitoring data, is the prior PDF of parameters, is the posterior PDF of parameters based on the observations and is the likelihood based on the given parameters .
When the initial PDF of the parameters is given, in order to obtain the posterior probability density function of the unknown parameters, the state equation is defined as [21]:
where the notation 0: means a set of parameters from cycles 0 to .
The new observations are collected at time . According to the Bayesian rule, the posterior probability density for unknown parameters updates over time, so posterior probability distribution of the current parameters is obtained [21]:
where is a constant.
Above is the prediction process and update process for parameters of Paris model. In this paper, we utilize the Bayesian filtering and Monte Carlo algorithm to obtain the parameters updating.
Assuming that update observations are known, the posterior probability density of parameters can be expressed as follows [21]:
where is the Dirac delta measure, is the priori vectors for parameters, is a set of vectors for parameters at cycles from 0 to k and is the priori probability density function. If we get the real posterior probability density function , Eq. (6) can be calculated according to Eq. (7) [21]:
where are independent random samples sampling from , is the number of samples sampling from .
In the calculation process, are multi-type and non-standard. Therefore, it is difficult to obtain the result. In order to calculate the posterior probability density function of parameters for Paris model, the importance function sampling method is proposed in this paper. In this way, we can obtain the PDF distribution based on importance sampling for , which has the same distribution with the . Therefore, Eq. (7) can be transformed as follows [21]:
where is the weights of the unknown parameters, , , which can be calculated by sampling, and is the probability density function of observations.
In order to obtain the weight, we assume that , and the probability distribution can be expressed as follows:
where and .
3. Hybrid prediction approach for gear
3.1. Improved Paris law based on PF
In order to make full use of the advantages of data-driven method and model-based method, the integration of Paris law and PF model is proposed in this paper. The approach considers both the gear degradation process, and the prior information, which can describe the gear degradation process based on a simple model and improve the residual fatigue life prediction accuracy based on the prior information, which is the measured gear crack size as shown in Table 1. Based on the introduction of Paris law and PF model above, the state transition equation function for the Paris law is established, which is shown as follows:
The model parameters and as well as the degradation state are estimated using the gear crack growth information under constant amplitude loading.
When the state transition equation and crack growth prior information are defined, the parameters and over time can be estimated based on the PF model. Moreover, we can estimate the parameters online when new gear crack growth information is added. In this paper, the parameters of the improved Paris law are obtained by maximum likelihood estimation, and the likelihood function is shown as follows:
where and .
3.2. Implementation steps of hybrid prediction approach
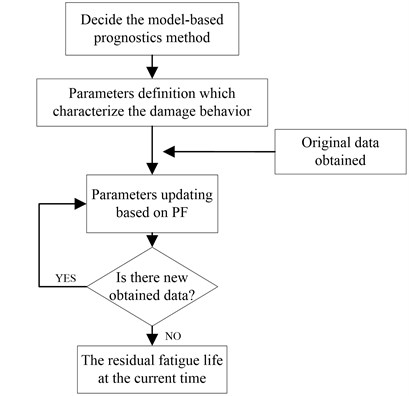
In the prediction strategy process, the integration of the Paris model and particle filter is proposed to predict the residual fatigue life of the gear with prior crack growth information. The implementation steps of the proposed approach are shown as Fig. 1. The steps are described as follows:
Step 1. Decide the model-based prognostics method according to the object of study and raw measurement data. We choose the Paris law as the model-based method in this paper.
Step 2. Define the parameters which characterize the damage behavior. The model parameters which have an effect on the model behavior are often unknown and need to be identified in the prediction process.
Step 3. PF is employed to update the parameters as the data-driven model when new observations appear.
Step 4. If there is a new observation, go back to Step 3, or else go to Step 5.
Step 5. The residual fatigue life at the current time can be obtained based on the updated parameters of the Paris law.
The proposed hybrid approach considers the model-based prognostics and data-driven model at the same time, which can improve the prediction performance.
Fig. 1Implementation of hybrid prediction approach
4. Case studies and discussion
4.1. Gear crack growth test
In order to verify the proposed method in this paper, a gear crack growth test is taken as an example to predict the residual fatigue life. As shown in Fig. 2, there is a through-the-thickness crack on the gear. The crack size is measured at every 50 cycles under the loading condition 78 MPa, which is shown in Table 1, and the critical threshold of the crack size is 0.0463 m. The actual fatigue life is 2500 cycles. All the original data is taken from Ref [20]. In the current paper, we establish the model based on the crack size, not considering the relationship between the gear crack and condition monitoring data, such as vibration and temperature. Firstly, the true crack size data are generated according to Eq. (10). The measured crack size data are then generated by multiplying noise, which is lognormally distributed with standard deviation of 0.001/ (m). Actually, it has been shown that the distribution of crack size follows a lognormal distribution [22].
Fig. 2Gear crack

Table 1Monitoring data for crack growth [20]
Time (cycles) | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
Crack size (m) | 0.0103 | 0.0118 | 0.0095 | 0.0085 | 0.0122 | 0.0110 | 0.0120 | 0.0113 |
Time (cycles) | 450 | 500 | 550 | 600 | 650 | 700 | 750 | 800 |
Crack size (m) | 0.0122 | 0.0110 | 0.0124 | 0.0117 | 0.0138 | 0.0127 | 0.0115 | 0.0135 |
Time (cycles) | 850 | 900 | 950 | 1000 | 1050 | 1100 | 1150 | 1200 |
Crack size (m) | 0.0124 | 0.0141 | 0.0160 | 0.0157 | 0.0149 | 0.0156 | 0.0153 | 0.0155 |
4.2. Degradation process and parameters updating
As shown in Fig. 3, the measured crack size increases gradually over cycles, which means that the trend of the gear degradation. It is assumed that the standard deviation of measurement is known. Also, the initial distribution of the parameters and the likelihood function are, respectively, normal and lognormal distributions, which are as follows: (0.01, (5×10–4)2), (4, 0.22), (–22.33, 1.122).
Fig. 3Monitoring crack size
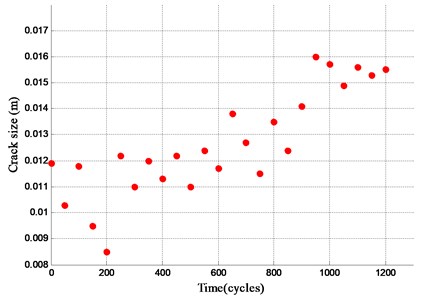
According to the prior information of gear crack size data, we can predict the gear degradation process based on the proposed hybrid approach with the initial distribution of the parameters. The state transition for gear crack growth is given by Eq. (10).
The gear degradation in the future can be predicted, and the predicted crack size is shown in Table 2. Moreover, the gear crack growth is shown in Fig. 4, and we can tell that the gear is close to failure at 2500 cycles according to the failure threshold, which is fit with the actual residual life of the gear.
Fig. 4Crack growth prediction
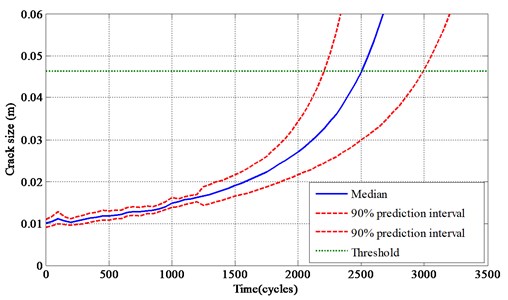
Table 2Predicted data for crack growth
Time (cycles) | 1250 | 1300 | 1350 | 1400 | 1450 | 1500 | 1550 | 1600 |
Crack size (m) | 0.0165 | 0.0170 | 0.0175 | 0.0180 | 0.0184 | 0.0190 | 0.0196 | 0.0203 |
Time (cycles) | 1650 | 1700 | 1750 | 1800 | 1850 | 1900 | 1950 | 2000 |
Crack size (m) | 0.0209 | 0.0220 | 0.0223 | 0.0231 | 0.0241 | 0.0250 | 0.0260 | 0.0271 |
Time (cycles) | 2050 | 2100 | 2150 | 2200 | 2250 | 2300 | 2350 | 2400 |
Crack size (m) | 0.0283 | 0.0296 | 0.0310 | 0.0352 | 0.0343 | 0.0360 | 0.0381 | 0.0405 |
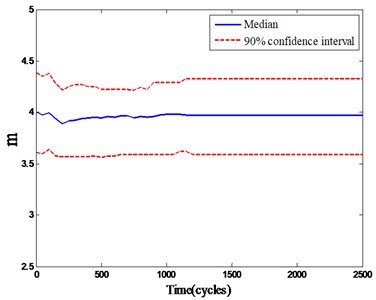
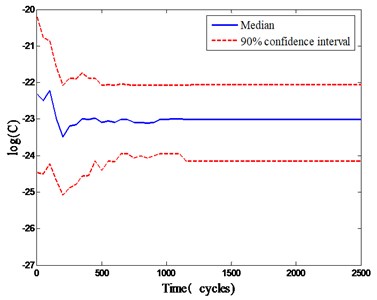
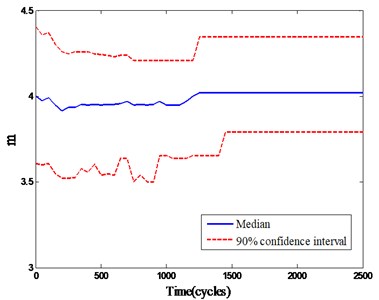
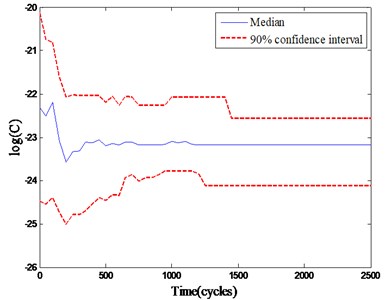
While the gear degradation process is predicted based on the PF model, the parameters of Paris model are updated simultaneously. When the gear crack size in the future is predicted, we can update the model parameters based on the new obtained crack size data. Taking the parameters estimation at 1200 cycles and 1500 cycles as examples, initial value 3.8, 1.5×10–10 and historical data are both generated based on PF to get the best estimation for the gear degradation state (, , ) and (, , ), which are shown in Fig. 5 and Fig. 6, and the model parameters are convergent to the optimum value quickly. According to the gear crack size and the model parameters, we can estimate the residual fatigue life at the current time.
Fig. 5Updated parameters at 1200 cycles
a)
b)
Fig. 6Updated parameters at 1500 cycles
a)
b)
4.3. Prediction results and discussion
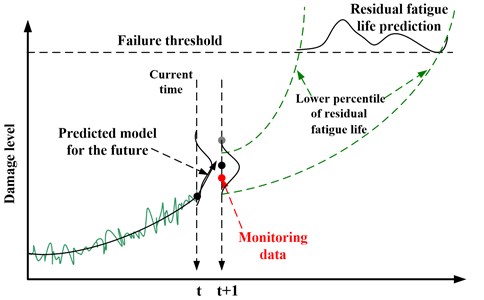
The process of residual fatigue life prediction is shown in Fig. 7. Firstly, the prediction model needs to be defined based on the investigated object, and the model parameters are obtained according to the prior information, which has been finished in section 4.2. However, we can only get a lower accuracy result based on the model. Therefore, new monitoring information is added to the predicted process, and posterior parameters of the model can be obtained, which can improve the accuracy and update the parameters online. Finally, the residual fatigue life can be obtained according to the given failure threshold.
Fig. 7Illustration of RFL prediction
The model parameters are given at 1200 cycles and 1500 cycles as mentioned above. Consequently, the residual fatigue life distribution is shown in Fig. 8 and Fig. 9 respectively, which takes 5000 particles in every simulation. According to the residual fatigue life distribution and the result of the residual fatigue life at the current time, we can obtain the probability density function, which is more suitable for describing the gear residual fatigue life.
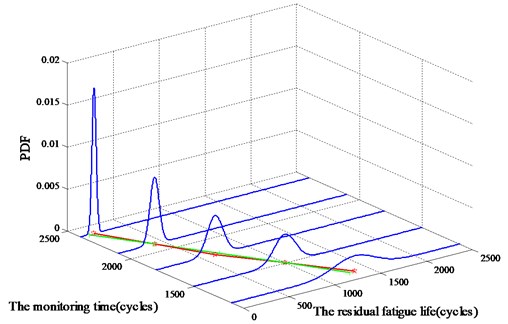
Taking the calculation process above repeated, then the gear residual fatigue life can be obtained over time gradually. The gear residual fatigue life and 90 % confidence interval at a different time can be calculated based on the model when the parameters and failure threshold are given as shown in Table 3. The probability density function of the gear residual fatigue life is shown in Fig. 10, and the red curve and green curve represents the predicted mean residual fatigue life and actual residual fatigue life, respectively. The variances of the probability density function are smaller over cycles with more monitored and predicted crack size data is used during the prediction process, and it means that the prediction results are more and more accurate.
Fig. 8Residual fatigue life distribution at 1200 cycles
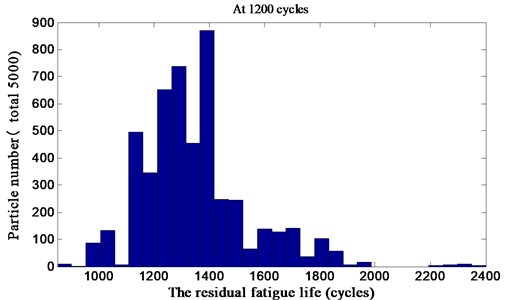
Fig. 9Residual fatigue life distribution at 1500 cycles
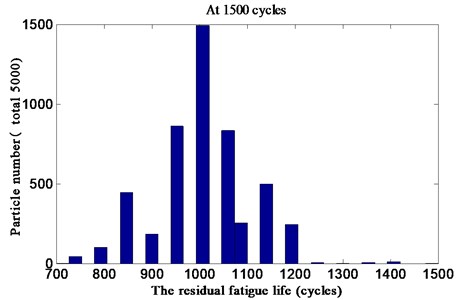
Table 3Predicted RFL and 90 % confidence interval
Time (cycles) | Prediction of RFL (cycles) | Actual RFL (cycles) | Confidence interval | |
90 % lower limit | 90 % upper limit | |||
1200 | 1350 | 1300 | 1000 | 1750 |
1500 | 1000 | 1000 | 800 | 1200 |
1800 | 650 | 700 | 550 | 850 |
2100 | 400 | 400 | 300 | 500 |
2400 | 150 | 100 | 100 | 200 |
Fig. 10Residual fatigue life probability density function
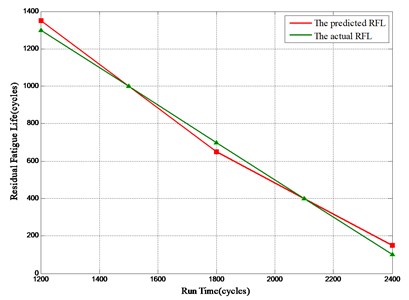
The predicted residual fatigue life and actual fatigue life are compared as shown in Fig. 11. The predicted results are closer to the actual residual gear fatigue life with the increase of monitored data. The gear degradation process allows to the Paris law, and the model parameters are updated by the PF, which can make full use of both the prior information of gear crack, and the posterior information. However, we only study the residual fatigue life prediction under the constant amplitude loading, and the case under variable amplitude loading needs a further study. The results errors are caused by the monitoring information errors and the randomness of the proposed model, however, the model accuracy satisfies with the most working condition. In addition, when the gear is close to a failure, the error is much bigger, which is caused by the change of the mechanical properties.
Fig. 11Comparison of actual and predicted RFL
5. Conclusions
A hybrid residual fatigue life prediction approach based on the PF model and Paris law is proposed in this paper. Firstly, the Paris law is utilized to describe the crack growth of the gear. Then, the parameters of Paris law are updated and the gear degradation in the future are predicted based on the PF model. Compared with the failure threshold of the gear, the residual fatigue life can be obtained. The main findings are as follows.
1) The Paris law can describe the gear crack growth process, and it is suitable to predict the residual gear fatigue life.
2) The improved Paris law utilizes the particle filtering to assess both model parameters and gear crack size simultaneously that is especially suitable for processing the nonlinear and non-Gaussian systems. In this way, we can update the parameters online and make full use of the prior information.
3) The integration of data-driven approach and model-based approach for residual fatigue life prediction can be used to improve the prediction performance, which provides a new way to predict the residual fatigue life.
References
-
Ahmed Mutahir, Ullah Himayat, Rauf A. Fracture mechanics based fatigue life estimation of axial compressor blade. 13th International Bhurban Conference on Applied Sciences and Technology, Islamabad, Pakistan, 2016, p. 69-74.
-
Dong Xu, Jin’e Huang, Qin Zhu, et al. Residual fatigue life prediction of ball bearings based on paris law and RMS. Chinese Journal of Mechanical Engineering, Vol. 25, Issue 2, 2012, p. 320-327.
-
Jardine A. K. S., Lin D., Banjevic D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mechanical Systems and Signal Processing, Vol. 20, 2006, p. 1483-1510.
-
Khader Iyas, Rasche Stefan, Lube Tanja, et al. Lifetime prediction of ceramic components - A case study on hybrid rolling contact. Engineering Fracture Mechanicas, Vol. 169, 2017, p. 292-308.
-
Rabiei Elaheh, Lopez Droguett Enrique Modarres Mohammad A prognostics approach based on the evolution of damage precursors using dynamic Bayesian networks. Advances in Mechanical Engineering, Vol. 8, Issue 9, 2016, https://doi.org/10.1177/1687814016666747.
-
Wang Yiwei, Binaud Nicolas, Gogu Christian, et al. Determination of Paris’ law constants and crack length evolution via extended and unscented Kalman filter: An application to aircraft fuselage panels. Mechanical Systems and Signal Processing, Vol. 80, 2016, p. 262-281.
-
Zhang Junhong, Yang Shuo, LiuJiewei Fatigue crack growth rate of Ti-6Al-4V considering the effects of fracture toughness and crack closure. Chinese Journal of Mechanical Engineering, Vol. 28, Issue 2, 2015, p. 409-415.
-
Alberto Carpinteri, Marco Paggi Self-similarity and crack growth instability in the correlation between the Paris’ constants. Engineering Fracture Mechanics, Vol. 74, 2007, p. 1041-1053.
-
Agafonov S. K. Vibration strength of structures based on the theory of cracking and fatigue curves. Journal of Machinery Manufacture and Reliability, Vol. 45, Issue 5, 2016, p. 451-457.
-
Loutas Theodoros, Eleftheroglou Nick, Zarouchas Dimitrios A data-driven probabilistic framework towards the in-situ prognostics of fatigue life of composites based on acoustic emission data. Composite Structures, Vol. 161, 2017, p. 522-529.
-
Annamalai K., Sathyanarayanan S., Naiju, C. D., et al. Fatigue life prediction of girth gear-pinion assembly used in kilns by finite element analysis. 2nd International Conference on Advanced Materials Design and Mechanics, Kuala Lumpur, Malaysia, 2013, p. 292-296.
-
Bhardwaj G., Singh S. K., Singh I. V., et al. Fatigue crack growth analysis of an interfacial crack in heterogeneous materials using homogenized XIGA. Theoretical and Application Fracture Mechanics, Vol. 85, 2016, p. 294-319.
-
Qian Yuning, Yan Ruqiang, Gao Robert X. A multi-time scale approach to remaining useful life prediction in rolling bearing. Mechanical Systems and Signal Processing, Vol. 83, Issue 2, 2017, p. 549-567.
-
Ben Abdessalem Anis, Azais Romain, Touzet-Cortina Marie, et al. Stochastic modelling and prediction of fatigue crack propagation using piecewise-deterministic Markov processes. Proceedings of the Institution of Mechanical Engineers Part O-Journal of Risk and Reliability, Vol. 240, Issue 4, 2016, p. 405-416.
-
Bernasconi A., Jamil A., Moroni F., et al. A study on fatigue crack propagation in thick composite adhesively bonded joints. International Journal of Fatigue, Vol. 50, 2013, p. 18-25.
-
Melgar M., Gomez-Jimenez C., Cot L. D., et al. Paris law parameter identification based on the extended Kalman filter. 3rd International Conference on Structural Nonlinear Dynamics and Diagnosis (CSNDD), Marrakech, Morocco, 2016.
-
Butler Shane, RingwoodJohn Particle filters for remaining useful life estimation of abatement equipment used in semiconductor manufacturing. Conference on Control and Fault Tolerant Systems Nice, France, 2010, p. 436-441.
-
Fan Bin, Hu Lei, Hu Niaoqing Remaining useful life prediction of rolling bearings by the particle filter method based on degradation Tate tracking. Journal of Vibroengineering, Vol. 17, Issue 2, 2015, p. 743-756.
-
Paris P. C., Erdogan F. A critical analysis of crack propagation laws. Journal of Basic Engineering, Vol. 85, 1963, p. 528-534.
-
Dawn An, Joo Ho Choi, Nam Ho Kim Prognostics 101: A tutorial for particle filter-based prognostics algorithm using Matlab. Reliability Engineering and System Safety, Vol. 115, 2013, p. 161-169.
-
Sun Lei Research on Methods and Application for Condition Based Equipment Fault Prognosis and Maintenance. Mechanical Engineering College, 2014.
-
Wang X., Rabiei M., Hurtado J., et al. A probabilistic-based airframe integrity management model. Reliability Engineering and System Safety, Vol. 94, 2009, p. 932-941.
Cited by
About this article
The research is supported by the National Natural Science Foundation of China (No. 71401173) and the authors are grateful to all the reviewers and the editor for their valuable comments.
