Strain modal analysis and fatigue residual life prediction of vibrating screen beam

1. Introduction

Large vibrating screen is widely used for screening, grading and dewatering in mining, metallurgy and chemical industries [1-3]. In the working process the beam of the vibrating screen is impacted by the particles and corroded by slime water, which result in fatigue fracture of the beam and suspended production [4]. If the fatigue crack of the beam is diagnosed and the fatigue residual life of the beam is predicted, production accidents and economic losses could be avoided. The strain modal parameters is more sensitive to fatigue cracks than the displacement modal parameters [5], so strain modal analysis is used for damage identification in the vibrating screen beam. Adewuyi and Wu used modal macro-strain flexibility methods for damage localization in flexural structures [6]. He et al. proposed a method that requires low-frequency modes and does not require mass normalization of parameters, thus making the method suitable for nondestructive dynamic damage detection of large structures under ambient excitation [7]. Cha and Buyukozturk used modal strain energy as a damage index in structural health monitoring and proposed hybrid multi-objective optimization algorithms to detect minor damages in various three-dimensional steel structures [8].

In this study, we built sensitive and reliable damage index of the vibrating screen beam based on strain modal analysis, which can predict the damaged extent and location of the beam. Then according to the fatigue crack length, the fatigue crack propagation residual life is predicted by the Paris law.

2. Damage identification theory based on strain modal analysis

The vibrating screen is a multiple degrees of freedom system, the free vibration equation is:

where $\mathbf{M}$, $\mathbf{C}$ and $\mathbf{K}$ are the mass, the damping and the stiffness matrices, respectively [9].

From Eq. (1) we can get:

where ${\omega }_i$ is the $i$th modal frequency, ${\mathbf{\Phi }}_i$ is the $i$th mode shape.

According to finite element theory, the relationship between strain mode shape ${\mathbf{\Psi }}^{\epsilon }$ and displacement mode shape $\mathbf{\Phi }$ is:

where $D$ is the linear differential operator, $\mathbf{P}$ is displacement function matrix, $\mathbf{A}$ is numerical matrix, $\mathbf{\beta }$ is coordinate transformation matrix [10].

Substituted Eq. (3) into Eq. (2), we can get:

Compared Eq. (2) and Eq. (5), the displacement mode is corresponding to the strain mode and both have the same modal frequency, modal mass and modal stiffness.

When the vibrating screen structure generates fatigue crack, its stiffness, frequency and mode shape is different from the intact structure, which is:

Accordingly, the strain modal parameters is varied:

The damage location and damage extent can be predicted by the variation of the modal stiffness, modal frequency or the mode shape theoretically. In fact, the fatigue crack damage mainly lead to the local stiffness varied, so the variation of the modal frequencies and displacement mode shapes are small, while the variation of the strain mode shape is large [11, 12].

In order to improve the effectiveness and reliability of the fatigue damage diagnosis result, we recommend the strain modal change ratio ($SR$) as the damage index:

where $m$ is the effective mode orders.

3. Displacement and strain modal analysis of the vibrating screen beam

In this paper, we select the 27 m² large linear vibrating screen as the research object, its finite element model is shown in Fig. 1. The beam of the vibrating screen is tubular beam structure, its inner diameter is 300 mm, outside diameter is 320 mm, thickness is 10 mm and beam length is 3 600 mm. The material of the beam is 20 carbon steel, its elastic modulus is 213 GPa, density is 7.8×10³ kg/m³, Poisson’s ratio is 0.28. Because the beam is thin-walled tube structure, the shell element of SHELL181 with six degrees of freedom and 4 nodes is more suitable than beam element for finite element modal analysis [13].

The locations of the fatigue crack for the beam often generate at the midpoint and quarter of the beam, so the locations of the simulated fatigue crack are assumed at the midpoint and quarter of the No. 4 beam in FEM model. The fatigue crack is assumed a transverse perforation crack with width of 1 mm, as shown in Fig. 2 [14, 15].

Fig. 1Finite element model of the vibrating screen

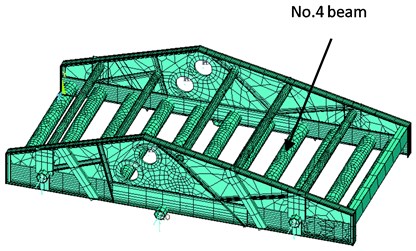
Fig. 2The simulated fatigue crack of the No. 4 beam

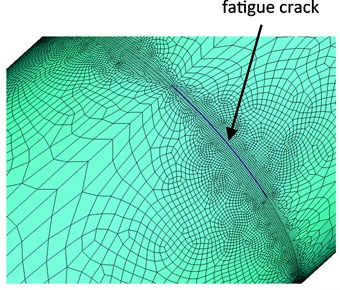
The beam of the vibrating screen is tubular structure, so the fatigue crack is shell crack type. The critical crack length of the beam can be calculated by Eq. (9):

where $K_{IC}$ is fracture toughness, $f$ is geometrical factor, ${\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum cyclic stress [16, 17]. Since the material of the beam is 20 carbon steel, $K_{IC}=$104 MPa·m^1/2, $f=$1.5, ${\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}=$60 MPa. the critical crack length $a_c$ is equal to 425 mm. In order to analyze the relationship between strain modal change ratio and the fatigue residual life of the beam, the displacement and strain modal parameters were calculated according 10 % to 90 % of the critical crack size, respectively (i.e., beam fatigue damage degree).

The beam was meshed with SHELL181 element, which has 12950 nodes and 12884 elements. The Block Lanczos method was used to extract the modal parameters, the first five modal frequencies of the intact and damaged beam are shown in Table 1, the relative deviation is $\eta =\left(f_p-f_c\right)/f_p$. The modal frequencies of the damaged beam decrease compared to intact beam as shown in Table 1. The reason is the fatigue crack caused the stiffness reduction for the damaged beam but the mass remains the same compared to intact beam, according to the Eq. (2), the modal frequency values must be reduced. The maximum relative deviation of the modal frequency is 4.06 % before and after damage. As the modal frequencies have not obviously change before and after damage, using modal frequency as index of damage detection is not effective and hard to judge the damage location.

The displacement and strain modal parameters of the finite element model were calculated, the first order of the displacement mode shape is shown in Fig. 3(a), the strain mode shape is shown in Fig. 3(b) when the beam damaged 60 percent. The maximum amplitude of the modal strain generates at the midpoint along the beam length direction because of the fatigue crack existence.

Since Fig. 3 is contour plot which is inconvenient to quantify the strain modal change rate, so we selected the generatrix along the beam length direction and analyzed strain modal change tendency along the beam length. When the beam fatigue damage degree is 30 percent, the first 3 mode shapes are shown in Fig. 4. Fig. 4(a) is the displacement mode shape, which is not visible mutation when the beam generate fatigue crack, Fig. 4(b) is the strain mode shapes, which has mutation peaks at the quarter and midpoint of the beam because of the fatigue crack. Fig. 4 shows that strain modal parameters are more sensitive to the crack damage than the displacement modal parameters. Thus, according to Eq. (8), we select the strain modal change ratio ($SR$) as the damage index which is sensitive and effective.

Fig. 3The first mode of the beam damaged 60 percent

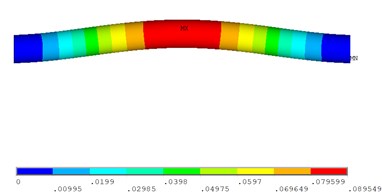
a) The first displacement mode shape

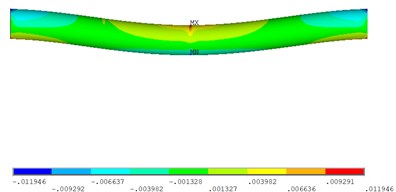
b) The first strain mode shape

Fig. 4The first 3 displacement and strain mode shapes

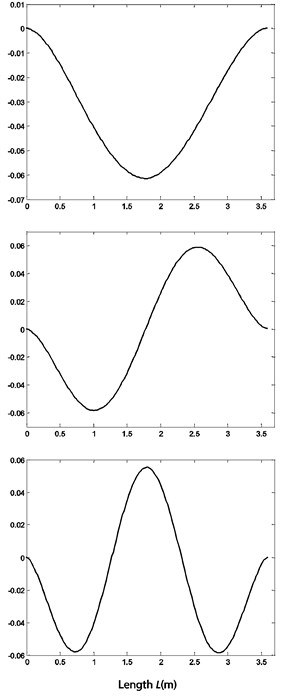
a) Displacement mode shapes

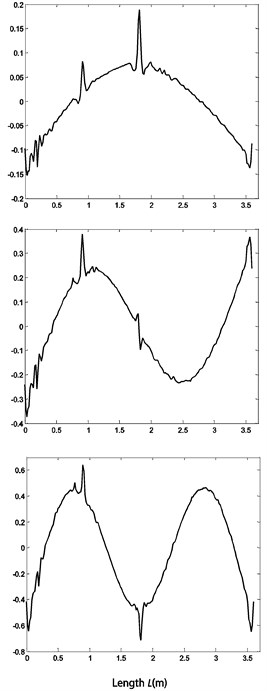
b) Strain mode shapes

The comparison of the strain mode shapes with different damage degree is shown in Fig. 5, the strain mode shapes generate mutation peak at the damaged location. The amplitudes of the mutation peak increase with the damage degree increasing at the quarter and midpoint of the beam. The reason is with the damage degree increasing the fatigue crack length extend, which lead to the stiffness of the structure decrease at the damaged location.

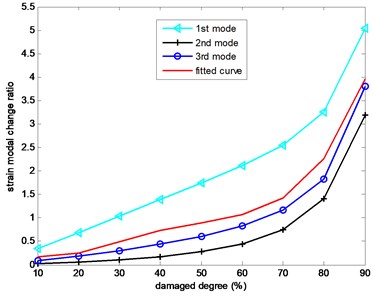
The strain modal change ratios with different damage degree are shown in Fig. 6, including the first 3 strain modes and the least squares fitting values. With the damage degree increase, the strain modal change ratios increase with similar trend among the strain modes. When the damage degree is less than 60 %, the strain modal ratio increase with slow steady growth, but after the damage degree is more than 60 %, the strain modal ratio increase rapidly with the crack propagation. The relationship between the damage degree and the strain modal change ratio can be fitted by least square method as shown in Eq. (10):

Fig. 5The first order strain mode shapes versus different damage degree

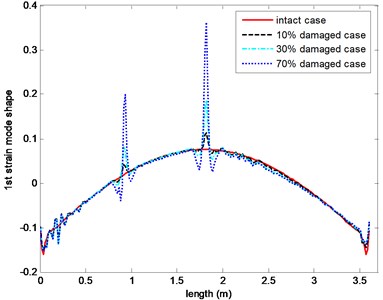
Fig. 6The strain modal change ratio versus different damage degree

4. The fatigue residual life of the vibrating screen beam

The fatigue life of the vibrating screen beam includes crack initiation life and crack propagation life. When the stress intensity factor $K_I$ is greater than the fatigue crack propagation threshold $\mathrm{\Delta }{K}_{th}$, the crack growth is in a stable stage, the relationship between the crack propagation rate $da/dN$ and $K_I$-factor range $\mathrm{\Delta }{K}_I$ can be described by Paris law:

where $a$ is crack length, $N$ is number of loading cycles, $C\text{,}$$m$ is material constant, $C=$2.11×10^-11, $m=$2.48:

Substitute Eq. (12) into Eq. (11) and integral, fatigue crack propagation residual life $N_f$ can be deduced:

where $a_c$ is critical crack length, $a_0$ is initial crack length, $f$ is geometrical factor, $\mathrm{\Delta }\sigma$ is stress amplitude [18].

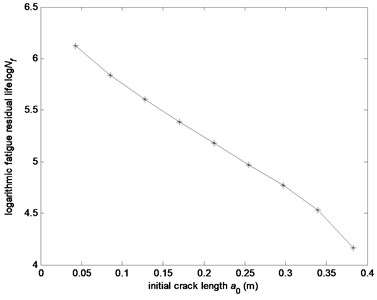
The relationship between initial crack length and the logarithmic fatigue residual life is shown in Fig. 7, with the increase of initial crack length, the crack propagation residual life declined. When the initial crack length is less than 50 % of the critical crack length, the crack propagation residual life declines rapidly.

Therefore, based on the strain modal analysis, the relationship between the strain modal change ratio and damage degree can be expressed by Eq. (10), the initial crack length is equivalent to the damage degree, then the fatigue crack propagation residual life can be calculated by Eq. (13).

Fig. 7The fatigue residual life versus different initial crack length

5. Conclusions

The displacement and strain modal analysis of the damaged beam were carried out, the results show that the modal frequencies deviation of the damaged beam is small compared to the intact beam, the displacement mode shapes have no obvious change likewise, but the strain mode shapes have mutation peaks at the damaged location. From the modal analysis results we found that taking the strain modal change ratio as the damage index has advantages of high sensitivity and good reliability. The strain modal change ratio can be calculated according to the damage degree of the beam, then the fatigue crack propagation residual life can be calculated by Paris law according to the initial crack length.