Nonlinear rotor dynamics on turbo expander with unbalanced bearing force caused by temperature difference

Li, Ming; Li, Cheng; Liu, Xianbo; Li, Hongguang; Li, Fucai; Meng, Guang

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2015

Check for updates

Nonlinear rotor dynamics on turbo expander with unbalanced bearing force caused by temperature difference

Ming Li¹

Cheng Li²

Xianbo Liu³

Hongguang Li⁴

Fucai Li⁵

Guang Meng⁶

^{1, 2, 3, 4, 5, 6}State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai, 200240, China

Corresponding Author:

Hongguang Li

Cite the article Download PDF

Downloads 1401

Abstract

This paper dedicates on the non-dimensional nonlinear rotor dynamics analysis of a turbo expander under unbalanced bearing forces caused by the temperature difference. The turbo expander rotor system is abstracted to a strictly symmetric lumped parameter model. The influence of temperature difference is simplified to the ratio of oil viscosity, which is applied on Capone oil film model. 1-Dimensional and 2-Dimensional bifurcation analysis are implemented in order to obtain the dynamic characteristics of the turbo expander rotor system. It can be concluded that the compressor wheel and the expander wheel are of the same pattern of motion in spite of the existence of the temperature difference; High temperature difference results in a high entrance point of 1-periodic motion to quasi-periodic motion, but the entrance point keeps still when the ratio of viscosity reaches some critical value. The oil-whirl, first and second order oil whip of sliding bearings are the most important factors influencing the asymmetric vibration of the compressor wheel and the expander wheel.

1. Introduction

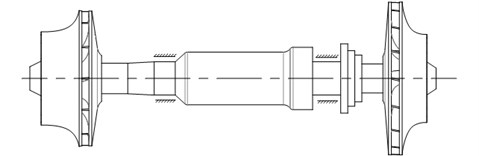
Nowadays, there is a great demand for liquefied oxygen, nitrogen or other constituents of liquefied air in the manufacturing industry, especially in the metallurgy industry and petrifaction industry. Air separation system is one of the best choice for producing liquefied air constituent by constituent. For many years, turbo expanders have been used in cryogenic processing plants to provide low temperature refrigeration [1], which produces relatively a huge amount of the total refrigerating output of the air separation system. The basic structure of the most widely used type of turbo expander without the outer casing is illustrated in Fig. 1.

It can be observed that the turbo expander is consisted of two wheels, two bearings and one shaft connecting them, which can be seen as the combination of two overhung rotor systems. This structure is quite similar with turbochargers in vehicle engine, so the research consequences of the turbocharger can also be referred in this research.

Fig. 1Rotor structure of turbo expander

Schmied [2] took Morton effect into stability analysis of the turbo expander rotor dynamics behavior. Wang [3] took static gas bearings into account for dynamic analysis of turbo expander. In the research of turbocharger, Whalley [4] considered only one side of turbocharger and evaluated the whirling frequencies. Kamesh [5] discussed the stabilization effects of gyroscopic moments because of the overhung. Ying [6] took foundation excitation into account and calculated the nonlinear behavior of a certain turbocharger. Tian [7] replaced common used sliding bearings with the full floating ring bearings in Ying’s model and discussed the linear behavior, stabilization and nonlinear behavior of the new system.

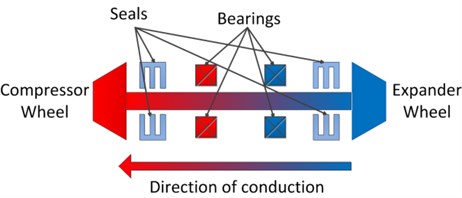
The basic structure and the influence of the temperature difference of the turbo expander is illustrated in Fig. 2, the wheels are called “Expander wheel” and “Compressor wheel” due to their functions respectively. In the retrieved papers discussed above, the bearings are always supposed to be working under the same lubricating situation and the oil-film forces are always treated as the same. However, when the turbo expander is working, the air pushes the expander wheel and cooling down because the internal energy of the air transforms into the kinetic energy of the expander wheel. The rotation of the expander wheel drives the compressor wheel to rotate, so the air passing the compressor wheel will be compressed and heated.

In the normal working condition, the expander wheel can reach –170~–180℃. Therefore there will exist a huge temperature gradient over 200°C between the compressor wheel and the expander wheel. The seals can prevent the cooling air reaching the bearings, however, the cooling capacity can also conduct along the shaft connecting two wheels and produce a temperature gradient across it, as Fig. 2 reveals. In the practical situation, when the turbo expander rotor system reaches a steady state, there will exist a temperature difference between two bearings, which can affect the lubricating behavior of the bearings to a certain extent.

Fig. 2Basic structure of turbo expander

In this paper, the temperature difference between two bearings is taken into account. The temperature difference between two bearings causes different viscosities in the bearings, which results in different and unbalanced oil-film forces. Non-dimensional dynamics equations with unbalanced bearing forces are established, and the nonlinear characteristics of them are obtained in order to investigate how the temperature difference will influence the turbo expander rotor system.

2. Governing equations

2.1. Rotor dynamics

In this study, the basic governing equations of rotor dynamics are based on lumped parameters method [8], which are also used in articles [6] and [7]. In this method, any ordinary rotor system can be decomposed into two basic components: discs and shafts. Fig. 3 illustrates the schematic of a disc and a shaft of lumped parameters method. Eq. (1) govern the behavior of the disc with the consideration of gyroscopic effect and Eq. (2) are the model of shaft based on Euler beam theory. In the turbo expander model, the wheels and the bearings can be treated as discs, and the shaft is broken apart into three separated shaft models:

1

\{\begin{matrix} m_{i} {\ddot{x}}_{i} + c_{i} {\dot{x}}_{i} = f_{x, i}^{L} - f_{x, i}^{R} - f_{b x, i} + m_{i} e_{i} ω^{2} \cos ω t, \\ J_{a i} {\ddot{ψ}}_{i} + c_{i} {\dot{ψ}}_{i} - ω J_{p i} {\dot{ϕ}}_{i} = - M_{y, i}^{L} + M_{y, i}^{R}, \\ m_{i} {\ddot{y}}_{i} + c_{i} {\dot{y}}_{i} = f_{y, i}^{L} - f_{y, i}^{R} - f_{b y, i} + m_{i} e_{i} ω^{2} \sin ω t, \\ J_{a i} {\ddot{ϕ}}_{i} + c_{i} {\dot{ϕ}}_{i} + ω J_{p i} {\dot{ψ}}_{i} = M_{x, i}^{L} - M_{x, i}^{R}, \end{matrix}

2

\{\begin{matrix} x_{i + 1} = x_{i} + l_{i} ψ_{i} + \frac{l_{i}^{2}}{2 {E I}_{i}} M_{y, i}^{R} + \frac{l_{i}^{3}}{6 {E I}_{i}} f_{x, i}^{R}, \\ ψ_{i + 1} = ψ_{i} + \frac{l_{i}}{{E I}_{i}} M_{y, i}^{R} + \frac{l_{i}^{2}}{2 {E I}_{i}} f_{x, i}^{R}, \\ M_{y, i + 1}^{L} = M_{y, i}^{R} + f_{x, i}^{R} l_{i}, \\ f_{x, i + 1}^{L} = f_{x, i}^{R}, \\ y_{i + 1} = y_{i} - l_{i} ϕ_{i} + \frac{l_{i}^{2}}{2 {E I}_{i}} M_{x, i}^{R} + \frac{l_{i}^{3}}{6 {E I}_{i}} f_{y, i}^{R}, \\ ϕ_{i + 1} = ϕ_{i} - \frac{l_{i}}{{E I}_{i}} M_{x, i}^{R} - \frac{l_{i}^{2}}{2 {E I}_{i}} f_{y, i}^{R}, \\ M_{x, i + 1}^{L} = M_{x, i}^{R} + f_{y, i}^{R} l_{i}, \\ f_{y, i + 1}^{L} = f_{y, i}^{R} . \end{matrix}

Fig. 3Schematic of disc and shaft of distributed parameters method

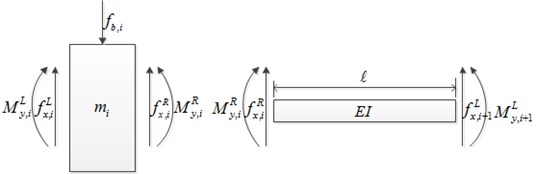
Fig. 4Abstract drawing of turbo expander rotor

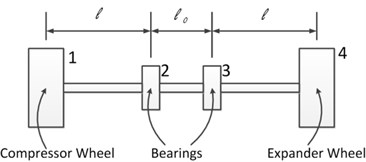
Fig. 4 shows the abstract drawing of the turbo expander rotor. The numbers in Fig. 4 are the serial numbers of the discs from the compressor wheel to the expander wheel. In this research, a strictly symmetrical structure of the turbo expander rotor system is adopted in order to avoid the influence of the unsymmetrical rotor structure. The influence of the temperature difference between two bearings is the only essential focused on.

2.2. Bearing forces

The most widely used sliding bearing oil-film force model in rotor dynamics was proposed by Capone [9] and be well-known in an article written by Adiletta [10]. This model is based on short-journal theory and be adopted in many articles [6-7, 11-12]. The non-dimensional oil-film force can be related to the actual oil-film force with the Sommerfeld variable $σ$ :

3

f_{b x, i} = σ F_{b x, i}, f_{b y, i} = σ F_{b y, i} .

For a certain bearing, $σ$ can be represented by the viscosity $μ$ , the rotating speed $ω$ , the length of bearing $L$ , the radius of bearing $R$ and the clearance of bearing $C$ :

4

σ = μ ω R L {(\frac{R}{C})}^{2} {(\frac{L}{2 R})}^{2} .

The non-dimensional oil-film force can be written as Eq. (5):

5

\{\begin{matrix} F_{b x, i} \\ F_{b y, i} \end{matrix}\} = \frac{\sqrt{{(X - 2 \dot{Y})}^{2} + {(Y + 2 \dot{X})}^{2}}}{1 - X^{2} - Y^{2}} \{\begin{matrix} 3 X V (X, Y, α) - \sin α G (X, Y, α) - 2 \cos α S (X, Y, α) \\ 3 Y V (X, Y, α) + \cos α G (X, Y, α) - 2 \sin α S (X, Y, α) \end{matrix}\} .

Herein:

6

\{\begin{matrix} α = \tan^{- 1} (\frac{Y + 2 \dot{X}}{X - 2 \dot{Y}}) - \frac{π}{2} s g n (\frac{Y + 2 \dot{X}}{X - 2 \dot{Y}}) - \frac{π}{2} (Y + 2 \dot{X}), \\ G (X, Y, α) = \frac{2}{\sqrt{1 - X^{2} - Y^{2}}} (\frac{π}{2} + \tan^{- 1} \frac{Y \cos α - X \sin α}{\sqrt{1 - X^{2} - Y^{2}}}), \\ V (X, Y, α) = \frac{2 + (Y \cos α - X \sin α) G (X, Y, α)}{1 - X^{2} - Y^{2}}, \\ S (X, Y, α) = \frac{X \cos α + Y \sin α}{1 - {(X \cos α + Y \sin α)}^{2}} . \end{matrix}

2.3. Temperature differences

Doolittle [13] discussed the dependence of the viscosity and the temperature of Newtonian flow. It can be concluded that the viscosity and the reciprocal of the temperature are logarithmically linear, which means the lower the temperature of oil, the higher its viscosity will be. This relationship can be shown by Walther equation Eq. (7) or Guzman-Andrade equation Eq. (8):

7

l n μ = \frac{B}{T} + l n A,

8

l o g l o g (μ + 0.8) = A l o g T + B .

In order to represent the relationship between the oil-film force and the temperature, a parameter of $λ$ is introduced to represent the viscosity ratio between the expander bearing force $f_{b x, 2}$ and the compressor bearing force $f_{b x, 3}$ , see Eq. (9). $λ$ is also the ratio of Sommerfeld variable because of the strictly symmetric condition:

9

λ = \frac{μ_{3}}{μ_{2}} = \frac{σ_{3}}{σ_{2}} .

Therefore the bearing forces can be expressed as:

10

f_{b x, 2} = σ F_{b x, 2}, f_{b x, 3} = λ σ F_{b x, 3} .

2.4. Non-dimensional equations

Non-dimensional equations are more suitable for the nonlinear dynamic analysis, suppose the non-dimensional displacement and rotational angle:

11

X_{i} = \frac{x_{i}}{C}, Y_{i} = \frac{y_{i}}{C}, Ψ_{i} = \frac{ψ_{i}}{\frac{π}{2}}, Φ_{i} = \frac{ϕ_{i}}{\frac{π}{2}} .

After that, several non-dimensional parameters can be derived from the original parameters. Because of the strictly symmetric condition, the compressor wheel and the expander wheel are the same, and so are the compressor bearing and the expander bearing. Suppose the variables of the wheels are expressed by the subscript $D$ and the bearings by the subscript $B$ , the non-dimensional parameters are shown in Eq. (12):

12

\{\begin{matrix} τ = ω t, Ω = \frac{ω}{ω_{1}}, ζ = \frac{c}{2 \sqrt{k m}}, {\bar{E I}}_{m} = \frac{E I}{l^{3} m_{D} ω_{1}^{2}}, δ = \frac{l}{C}, {\bar{E I}}_{j} = \frac{E I}{J_{a D} l ω_{1}^{2}}, \\ \bar{g} = \frac{g}{C}, α = \frac{J_{p D}}{J_{a D}} = \frac{J_{p B}}{J_{a B}}, \bar{m} = \frac{m_{B}}{m_{D}}, \bar{l} = \frac{l}{l_{0}}, β = \frac{J_{a D}}{J_{a B}}, \bar{σ} = \frac{σ}{C m_{B}}, \bar{e} = \frac{e}{C} . \end{matrix}

Then the non-dimensional equations of the turbo expander rotor system is shown in Eq. (13). The values of the non-dimensional parameters are listed in Table 1.

Table 1Value of non-dimensional parameters

Parameter	Value	Parameter	Value
$ζ$	0.1	${\bar{E I}}_{m}$	1.5
${\bar{E I}}_{J}$	6.5	$α$	2
$δ$	0.004	$β$	45
$\bar{l}$	1.5	$\bar{m}$	0.25
$\bar{σ}$	0.025	$\bar{g}$	0.0015
$\bar{e}$	0.5

3. Nonlinear analysis

3.1. 1-D bifurcation diagram analysis

Bifurcation diagram is the most common tool in nonlinear analysis. Different from other researches [6-7], in this study, there are two variables, $Ω$ and $λ$ , which affect the nonlinear behavior of the turbo expander system. As the classical bifurcation diagram in rotor dynamics research, the ratio of rotational speed $Ω$ is firstly selected as the bifurcation variable and $λ$ is fixed. Without loss of generality, $λ = 1.0, 10.0, 100.0$ are selected to represent the nonlinear dynamic behavior of the turbo expander rotor system with different temperature differences. Fig. 5 shows the bifurcation diagram when $λ = 1.0$ , in another word, there is not any influence of the temperature difference, which can be treated as the benchmark in this study.

13

\{\begin{matrix} {\ddot{X}}_{1} = - 2 \frac{ζ}{Ω} {\dot{X}}_{1} - \frac{12 {\bar{E I}}_{m}}{Ω^{2}} (X_{1} - X_{2}) - \frac{3 π {\bar{E I}}_{m}}{δ Ω^{2}} (Ψ_{1} + Ψ_{2}) + \cos τ, \\ {\ddot{Ψ}}_{1} = - 2 \frac{ζ}{Ω} {\dot{Ψ}}_{1} + α {\dot{Φ}}_{1} - \frac{12}{π} \frac{{\bar{E I}}_{J} δ}{Ω^{2}} (X_{1} - X_{2}) - \frac{2 {\bar{E I}}_{J}}{Ω^{2}} ({2 Ψ}_{1} + Ψ_{2}), \\ {\ddot{Y}}_{1} = - 2 \frac{ζ}{Ω} {\dot{Y}}_{1} - \frac{12 {\bar{E I}}_{m}}{Ω^{2}} (Y_{1} - Y_{2}) + \frac{3 π {\bar{E I}}_{m}}{δ Ω^{2}} (Φ_{1} + Φ_{2}) - \frac{\bar{g}}{Ω^{2}} + \sin τ, \\ {\ddot{Φ}}_{1} = - 2 \frac{ζ}{Ω} {\dot{Φ}}_{1} - α {\dot{Ψ}}_{1} + \frac{12}{π} \frac{{\bar{E I}}_{J} δ}{Ω^{2}} (Y_{1} - Y_{2}) - \frac{2 {\bar{E I}}_{J}}{Ω^{2}} ({2 Φ}_{1} + Φ_{2}), \\ {\ddot{X}}_{2} = - 2 \frac{ζ}{Ω} {\dot{X}}_{2} + \frac{12 {\bar{E I}}_{m}}{\bar{m} Ω^{2}} (X_{1} - X_{2}) + \frac{3 π {\bar{E I}}_{m}}{\bar{m} δ Ω^{2}} (Ψ_{1} + Ψ_{2}) \\ - \frac{12 {\bar{E I}}_{m}}{\bar{m} {\bar{l}}^{3} Ω^{2}} (X_{2} - X_{3}) - \frac{3 π {\bar{E I}}_{m}}{\bar{m} δ {\bar{l}}^{2} Ω^{2}} (Ψ_{2} + Ψ_{3}) - \frac{\bar{σ}}{Ω} F_{b x, 2}, \\ {\ddot{Ψ}}_{2} = - 2 \frac{ζ}{Ω} {\dot{Ψ}}_{2} + α {\dot{Φ}}_{2} - \frac{12}{π} \frac{{\bar{E I}}_{J} δ β}{Ω^{2}} (X_{1} - X_{2}) - \frac{2 {\bar{E I}}_{J} β}{Ω^{2}} (Ψ_{1} + 2 Ψ_{2}) \\ - \frac{12}{π} \frac{{\bar{E I}}_{J} δ β}{{\bar{l}}^{2} Ω^{2}} (X_{2} - X_{3}) - \frac{2 {\bar{E I}}_{J} β}{\bar{l} Ω^{2}} ({2 Ψ}_{2} + Ψ_{3}), \\ {\ddot{Y}}_{2} = - 2 \frac{ζ}{Ω} {\dot{Y}}_{2} + \frac{12 {\bar{E I}}_{m}}{\bar{m} Ω^{2}} (Y_{1} - Y_{2}) - \frac{3 π {\bar{E I}}_{m}}{\bar{m} δ Ω^{2}} (Φ_{1} + Φ_{2}) \\ - \frac{12 {\bar{E I}}_{m}}{\bar{m} {\bar{l}}^{3} Ω^{2}} (Y_{2} - Y_{3}) + \frac{3 π {\bar{E I}}_{m}}{\bar{m} δ {\bar{l}}^{2} Ω^{2}} (Φ_{2} + Φ_{3}) - \frac{\bar{g}}{Ω^{2}} - \frac{\bar{σ}}{Ω} F_{b y, 2}, \\ {\ddot{Φ}}_{2} = - 2 \frac{ζ}{Ω} {\dot{Φ}}_{2} - α {\dot{Ψ}}_{2} + \frac{12}{π} \frac{{\bar{E I}}_{J} δ β}{Ω^{2}} (Y_{1} - Y_{2}) - \frac{2 {\bar{E I}}_{J} β}{Ω^{2}} (Φ_{1} + 2 Φ_{2}) \\ + \frac{12}{π} \frac{{\bar{E I}}_{J} δ β}{{\bar{l}}^{2} Ω^{2}} (Y_{2} - Y_{3}) - \frac{2 {\bar{E I}}_{J} β}{\bar{l} Ω^{2}} ({2 Φ}_{2} + Φ_{3}), \\ {\ddot{X}}_{3} = - 2 \frac{ζ}{Ω} {\dot{X}}_{3} + \frac{12 {\bar{E I}}_{m}}{\bar{m} {\bar{l}}^{3} Ω^{2}} (X_{2} - X_{3}) + \frac{3 π {\bar{E I}}_{m}}{\bar{m} δ {\bar{l}}^{2} Ω^{2}} (Ψ_{2} + Ψ_{3}) \\ - \frac{12 {\bar{E I}}_{m}}{\bar{m} Ω^{2}} (X_{3} - X_{4}) - \frac{3 π {\bar{E I}}_{m}}{\bar{m} δ Ω^{2}} (Ψ_{3} + Ψ_{4}) - λ \frac{\bar{σ}}{Ω} F_{b x, 3}, \\ {\ddot{Ψ}}_{3} = - 2 \frac{ζ}{Ω} {\dot{Ψ}}_{3} + α {\dot{Φ}}_{3} - \frac{12}{π} \frac{{\bar{E I}}_{J} δ β}{{\bar{l}}^{2} Ω^{2}} (X_{2} - X_{3}) - \frac{2 {\bar{E I}}_{J} β}{\bar{l} Ω^{2}} (Ψ_{2} + {2 Ψ}_{3}) \\ - \frac{12}{π} \frac{{\bar{E I}}_{J} δ β}{Ω^{2}} (X_{3} - X_{4}) - \frac{2 {\bar{E I}}_{J} β}{Ω^{2}} ({2 Ψ}_{3} + Ψ_{4}), \\ {\ddot{Y}}_{3} = - 2 \frac{ζ}{Ω} {\dot{Y}}_{3} + \frac{12 {\bar{E I}}_{m}}{\bar{m} {\bar{l}}^{3} Ω^{2}} (Y_{2} - Y_{3}) - \frac{3 π {\bar{E I}}_{m}}{\bar{m} δ {\bar{l}}^{2} Ω^{2}} (Φ_{2} + Φ_{3}) \\ - \frac{12 {\bar{E I}}_{m}}{\bar{m} Ω^{2}} (Y_{3} - Y_{4}) + \frac{3 π {\bar{E I}}_{m}}{\bar{m} δ Ω^{2}} (Φ_{3} + Φ_{4}) - \frac{\bar{g}}{Ω^{2}} - λ \frac{\bar{σ}}{Ω} F_{b y, 3}, \\ {\ddot{Φ}}_{3} = - 2 \frac{ζ}{Ω} {\dot{Φ}}_{3} - α {\dot{Ψ}}_{3} + \frac{12}{π} \frac{{\bar{E I}}_{J} δ β}{{\bar{l}}^{2} Ω^{2}} (Y_{2} - Y_{3}) - \frac{2 {\bar{E I}}_{J} β}{\bar{l} Ω^{2}} (Φ_{2} + {2 Φ}_{3}) \\ + \frac{12}{π} \frac{{\bar{E I}}_{J} δ β}{Ω^{2}} (Y_{3} - Y_{4}) - \frac{2 {\bar{E I}}_{J} β}{Ω^{2}} ({2 Φ}_{3} + Φ_{4}), \\ {\ddot{X}}_{4} = - 2 \frac{ζ}{Ω} {\dot{X}}_{4} + \frac{12 {\bar{E I}}_{m}}{Ω^{2}} (X_{3} - X_{4}) + \frac{3 π {\bar{E I}}_{m}}{δ Ω^{2}} (Ψ_{3} + Ψ_{4}) + \cos τ, \\ {\ddot{Ψ}}_{4} = - 2 \frac{ζ}{Ω} {\dot{Ψ}}_{4} + α {\dot{Φ}}_{4} - \frac{12}{π} \frac{{\bar{E I}}_{J} δ}{Ω^{2}} (X_{3} - X_{4}) - \frac{2 {\bar{E I}}_{J}}{Ω^{2}} (Ψ_{3} + 2 Ψ_{4}), \\ {\ddot{Y}}_{4} = - 2 \frac{ζ}{Ω} {\dot{Y}}_{4} + \frac{12 {\bar{E I}}_{m}}{Ω^{2}} (Y_{3} - Y_{4}) - \frac{3 π {\bar{E I}}_{m}}{δ Ω^{2}} (Φ_{3} + Φ_{4}) - \frac{\bar{g}}{Ω^{2}} + \sin τ, \\ {\ddot{Φ}}_{4} = - 2 \frac{ζ}{Ω} {\dot{Φ}}_{4} - α {\dot{Ψ}}_{4} + \frac{12}{π} \frac{{\bar{E I}}_{J} δ}{Ω^{2}} (Y_{3} - Y_{4}) - \frac{2 {\bar{E I}}_{J}}{Ω^{2}} (Φ_{3} + 2 Φ_{4}), \end{matrix}

Fig. 5Bifurcation diagram λ=1.0

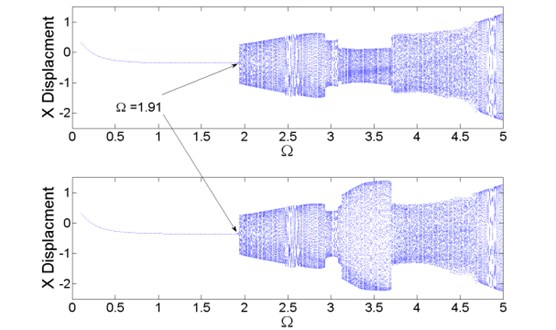
In Fig. 5, the upper diagram stands for the diagram of the compressor wheel, and the bottom one stands for the diagram of the expander wheel. From Fig. 5, it can be observed that as the growth of the non-dimensional speed, the motion of the turbo expander turns into quasi-periodic motion from 1-periodic motion at $Ω = 1.91,$ which is denoted as “entrance point”. In this bifurcation diagram, the quasi-periodic motion can also be divided into several sections. There is one violation of common sense, equal temperature does not produce two identical bifurcation diagram. When $Ω = 3.1 ~ 3.7$ , the vibration of the expander wheel is larger than which of the compressor wheel. Fig. 6 illustrates the orbit of rotor axis of the compressor wheel, the compressor bearing, the expander bearing and the expander wheel from left to right in different colors, with different rotational speeds and different motions.

Fig. 6Axis orbit of turbo expander wheels and bearings, λ=1.0

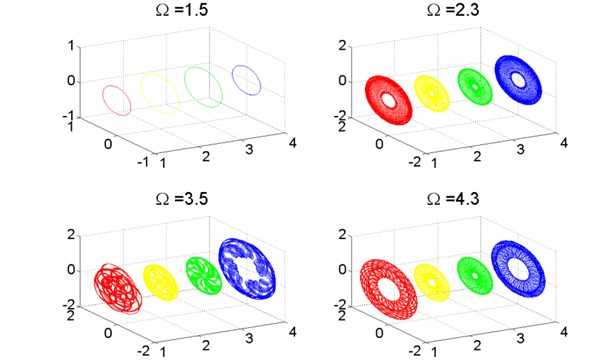
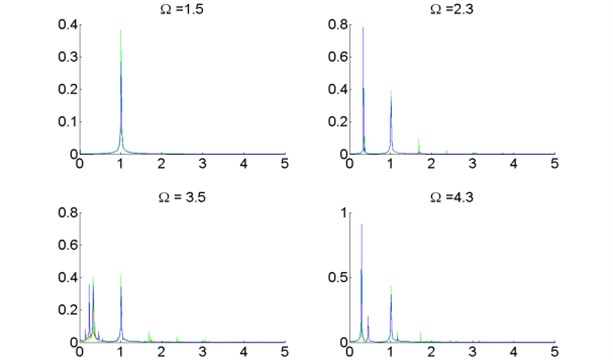
When $Ω = 1.5$ , the turbo expander rotor system is under 1-periodic motion, the vibration of the wheels and the bearings are symmetric. When the system enters quasi-periodic motion, the vibration of the wheels and the bearings becomes complex. When $Ω = 3.5$ , the vibration of the compressor wheel and the expander wheel turns into different and asymmetric, however, when $Ω = 4.3$ they are symmetric again. Fig. 7 shows the spectral diagrams of each wheels and bearings under different rotational speeds in different colors. It is clear enough that whatever the rotational speed is, the spectral diagrams of the wheels and the bearings coincide with each other.

This phenomenon can be interpreted in the following non-dimensional waterfall chart Fig. 7. Different from dimensional waterfall chart, the basic frequency exhibits as $f_{b a s i c} = 1$ instead of the synchronous line. From the waterfall chart it can be extrapolated that the quasi-periodic motion occurs on account of oil whirl, a frequency less than half of first order natural frequency but changes as the rotational speed grows is the characteristic.

Fig. 7Spectral diagrams of turbo expander wheels and bearings, λ=1.0

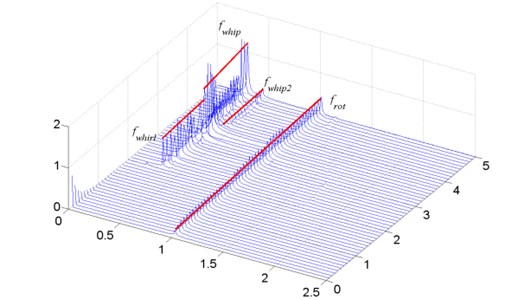
When the bearing reaches its first critical frequency, which is not coincidence of the natural frequency of the rotor system, oil whip happens. In the waterfall chart, the oil whip behaves as a frequency locking, the characteristic frequency does not alter as the rotational speed changes. The oil whip is the reason of asymmetric motion of the compressor wheel and the expander wheel; When the second critical frequency of the bearing is reached, the second order oil whip happens, which restricts the vibration of the turbo expander rotor and results in an approximate symmetric vibration of the two wheels. However, there is still a little differences exists. See Fig. 6.

Fig. 8Waterfall chart of turbo expander, λ=1.0

Similar with the analysis of $λ = 1.0$ , the bifurcation diagram of $λ = 10.0$ is illustrated in Fig. 9. It can be observed from it that the entrance point of 1-periodic motion to quasi-periodic motion is increased to $Ω = 2.22$ . The unbalanced viscosities of bearings cause a similar but of different vibration amplitudes motion pattern. In Fig. 9, the upper diagram stands for the compressor wheel and the other stands for the expander wheel.

In the section of $Ω = 0.1 ~ 2.22$ , the turbo expander rotor system is under 1-periodic motion, which is totally symmetric, as shown in Fig. 10. In the section of $Ω = 2.22 ~ 3.7$ , the expander wheel vibrates greater than the compressor wheel; in the following section the vibration of the compressor wheel surpass in reverse of the expander wheel. When the rotational speed ratio reaches about $Ω = 3. 9$ , the system recovers symmetric from the asymmetric motion. In Fig. 10, typical orbits of axis of $Ω = 1.5, 3.0, 3.8, 4.3$ are illustrated.

Fig. 9Bifurcation diagram, λ=10.0

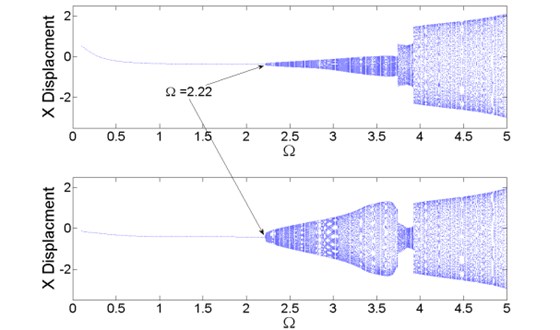
Fig. 10Axis orbit of turbo expander wheels and bearings, λ=10.0

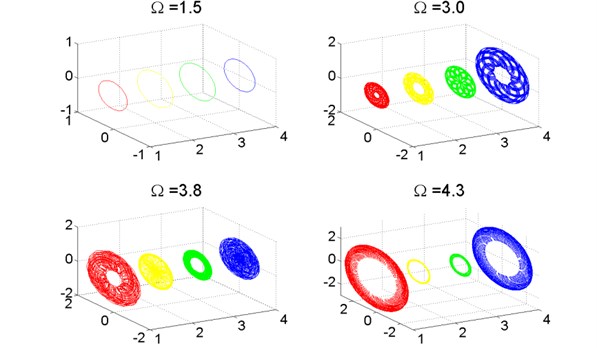
Fig. 11Spectral diagrams of turbo expander wheels and bearings, λ=10.0

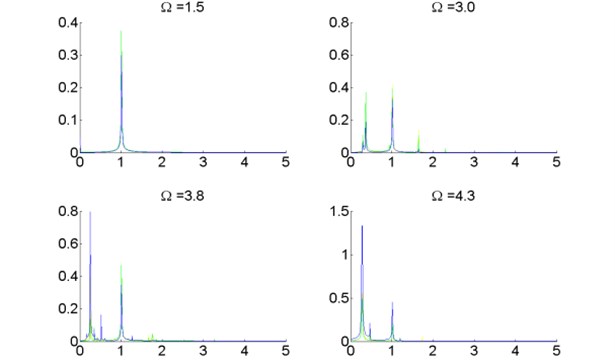
Fig. 11 also shows the spectral components of the bearings and the wheels under different rotational speeds. Similar with Fig. 7, the spectral components coincide with each other, which can be treated as the feature that the bearings and the wheels vibrate in the same pattern, the existence of $λ$ cannot force the bearings and the wheels vibrate differently.

The quasi-periodic motion is also caused by oil whirl with $λ = 10.0$ . Fig. 12 shows the waterfall chart. Oil whirl happens at $Ω = 2.22$ , which forces the expander wheel vibrates more fiercely than the compressor wheel. When the turbo expander rotor system reaches the first critical frequency of the bearing, oil whip happens, the vibration is suppressed. When the second critical frequency of the bearing is reached, second order oil whip occurs, the motion of the turbo expander is compelled to be approximately symmetric.

When $λ = 100.0$ , the entrance point of 1-periodic motion to quasi-periodic motion grows up to $Ω = 3.92$ , see Fig. 13.

Fig. 12Waterfall chart of turbo expander, λ=10.0

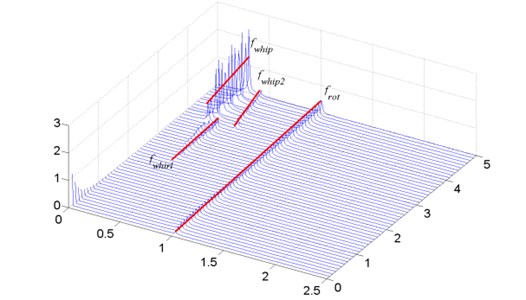
Fig. 13Bifurcation diagram, λ=100.0

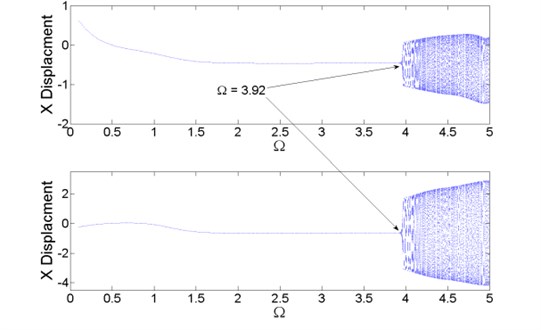
Fig. 14 shows three different vibration stage of the turbo expander with $λ = 100.0$ , and the spectral diagram is illustrated in Fig. 15. Similar with the research above, the existence of $λ$ does not affect the coincidence of the vibration patterns between the wheels and the bearings. The vibration amplitude of the expander wheel keeps higher than which of the compressor wheel in the quasi-periodic stage.

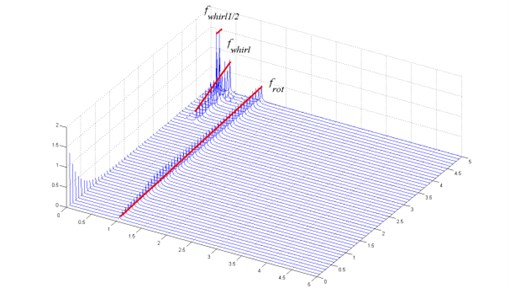
The waterfall chart is shown in Fig. 16. The quasi-periodic motion is also caused by the oil whirl of the bearings. There is a little different with the waterfall chart of $λ = 1.0$ and $λ = 10.0$ . When $Ω$ reaches 4.8, there exists a half oil whirl, the frequency of which is about a half of the frequency of oil whirl. However the influence of the half oil whirl is not as evident as the oil whirl.

From the research above, it can be identified that regardless of whether the ratio of oil viscosity exists, the vibration pattern of the compressor wheel and the expander wheel are the same, both of 1-periodic motion or quasi-periodic motion. However, the larger the ratio of oil viscosity, the higher the entrance point of 1-periodic to quasi-periodic is. The oil whirl and oil whip of bearings determine the detailed vibration conditions of the turbo expander rotor system, especially the amplitude relationship between the wheels and the bearings.

Fig. 14Axis orbit of turbo expander wheels and bearings, λ=100.0

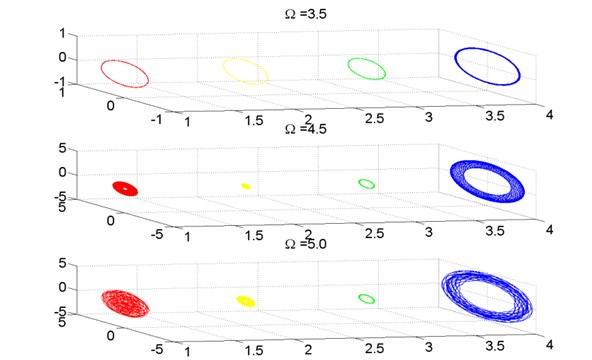
Fig. 15Spectral diagrams of turbo expander wheels and bearings, λ=100.0

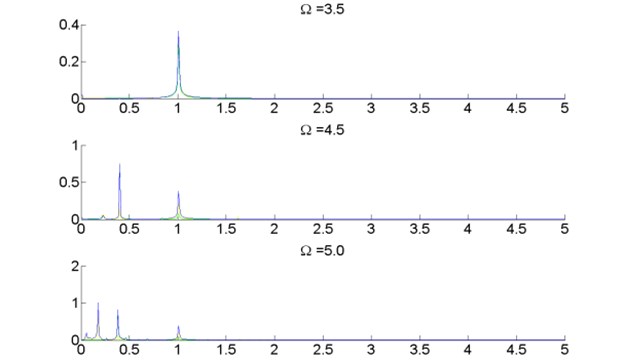
Fig. 16Waterfall chart of turbo expander, λ=100.0

3.2. 2-D bifurcation diagram analysis

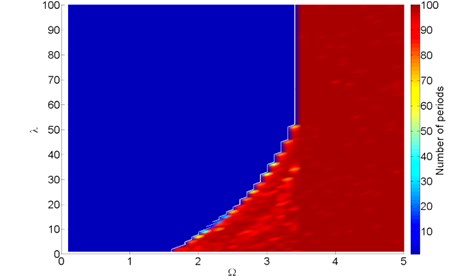
Form the analysis above, it can be concluded that the ratio of rotational speed $Ω$ and the ratio of oil viscosity or Sommerfeld variable $λ$ both dominates the nonlinear rotor dynamics behavior of the turbo expander. In the practical situation, the quasi-periodic motion of turbo expander rotor is not acceptable for its lack of controllability and stability. Fig. 17 shows a 2-dimensional bifurcation diagram of the turbo expander rotor system, $Ω$ and $λ$ are selected as axis $x$ and $y$ respectively and the color stands for the number of periods within 100 revolutions of the turbo expander rotor system, as the legend shows.

It can be observed that except for the conclusions obtain in 1D bifurcation analysis, the entrance point of 1-periodic motion to quasi-periodic motion has an exponential increase from $λ = 1$ to about $λ = 52$ . After that the entrance point does not move as the increase of $λ$ . Therefore, it can be concluded that working in the blue zone is safe for the turbo expander, which is reliable and stable. Outside the safety zone, rotor system of turbo expander is under quasi-periodic motion, which is dangerous and may cause malfunctions even faults. This figure can be referred in turbo expander design.

Fig. 172D bifurcation diagram

4. Conclusion remarks

The nonlinear analysis of the turbo expander rotor system with temperature difference results in several conclusion remarks, which are listed as follows:

1) The existence of the temperature difference does not produce different motion patterns between the compressor wheel and the expander wheel, they are always of 1-periodic motion or quasi-periodic motion simultaneously;

2) High temperature difference results in high entrance point of 1-periodic motion to quasi-periodic motion, but it does not change when temperature difference reached a critical value of about $λ = 52$ ;

3) The oil-whirl, first and second order oil whip of the bearings have a great influence in the vibration amplitude of the wheels, even asymmetric vibration occurs due to their existence.

Furthermore, in order to assure the turbo expander rotor system working in the safety zone and prevent the quasi-periodic motion or malfunctions, some sort of control laws should be adopted. First of all, the turbo expander rotor system should be designed to be working at an operating rotational speed under the entrance point. The most basic method is to control the temperature of the oil from the pump outlet, which is the most widely adopted way in the practical industry. Moreover, to control the vibration of turbo expander rotor system is also a suitable way. In article [14], the clearance of the bearing is controlled via the gap sensor, PZT actuator and a PID control law. In article [15], a squeeze mode MR fluid damper is used for vibration control of a rotor system. A suitable control system and law is important to prevent the turbo expander from malfunction or even fault, and our research group will focus on that in the next stage.

References

Bloch H. P., Soares C. Turboexpanders and Process Applications. Gulf Professional Publishing, Boston, 2001.

Search CrossRef
Schmied J., Pozivil J., Walch J. Hot spots in turboexpander bearings: case history, stability analysis, measurements and operational experience. Proceedings of ASME Turbo Expo, 2008, p. 9-13.

Search CrossRef
Wang X., Zhuang M., Zhang Q., Li S., Fu B. Dynamic stability study of static gas bearing for small cryogenic turbo-expander. Plasma Science and Technology, Vol. 13, Issue 4, 2011, p. 506.

Search CrossRef
Whalley R., Ebrahimi M., Abdul-Ameer A. High-speed rotor-shaft systems and whirling identification. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 221, Issue 6, 2007, p. 661-676.

Search CrossRef
Kamesh P., Brennan M.J., Holmes R. On the stabilising effect of gyroscopic moments in an automotive turbocharger. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 226, Issue 10, 2012, p. 2485-2495.

Search CrossRef
Ying G., Meng G., Jing J. Turbocharger rotor dynamics with foundation excitation. Archive of Applied Mechanics, Vol. 79, Issue 4, 2009, p. 287-299.

Search CrossRef
Tian L., Wang W., Peng Z. Dynamic behaviours of a full floating ring bearing supported turbocharger rotor with engine excitation. Journal of Sound and Vibration, Vol. 330, Issue 20, 2011, p. 4851-4874.

Search CrossRef
Rao J. S. History of Rotating Machinery Dynamics. Springer Verlag, Berlin, 2011.

Search CrossRef
Capone G. Analytical description of the fluid film force field in journal bearing. Energia Elettrica, Vol. 68, Issue 3, 1991, p. 105-110, (in Italian).

Search CrossRef
Adiletta G., Guido A., Rossi C. Chaotic motions of a rigid rotor in short journal bearings. Nonlinear Dynamics, Vol. 10, Issue 3, 1996, p. 251-269.

Search CrossRef
Jing J., Meng G., Sun Y., Xia S. On the oil-whipping of a rotor-bearing system by a continuum model. Applied mathematical modelling, Vol. 29, Issue 5, 2005, p. 461-475.

Search CrossRef
Cheng M., Meng G., Jing J. Non-linear dynamics of a rotor-bearing-seal system. Archive of Applied Mechanics, Vol. 76, Issue 3-4, 2006, p. 215-227.

Search CrossRef
Doolittle A. K. Studies in Newtonian flow. I. The dependence of the viscosity of liquids on temperature. Journal of Applied Physics, Vol. 22, Issue 8, 1951, p. 1031-1035.

Search CrossRef
Qiu J., Tani J., Kwon T. Control of self-excited vibration of a rotor system with active gas bearings. Journal of Vibration and Acoustics, Vol. 125, Issue 3, 2003, p. 328-334.

Search CrossRef
Wang J., Meng G., Hahn E. Experimental study on vibration properties and control of squeeze mode MR fluid damper-flexible rotor system. Proceedings of ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2003, p. 955-959.

Search CrossRef

About this article

Received

12 June 2014

Accepted

22 August 2014

Published

15 February 2015

SUBJECTS

Mechanical vibrations and applications

Keywords

turbo expander

temperature difference

nonlinear rotor dynamics

Acknowledgements

The authors are grateful for the supports received from the National Basic Research Program of China (973 Program, No. 2011CB706502).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.