Abstract
Pre-loading, both in terms of application method and actual applied force, significantly affects the stiffness and natural frequency of a high speed spindle system. The gyroscopic moment at high speed leads to whirling of the spindle, and the whirl frequency is not equal to the system’s natural frequency. To discover the relationship between pre-load and whirl frequency, theoretical and experimental research was undertaken. Two numerical models of the angular contact ball bearings, based on rigid and constant pre-load mechanisms, were established. The shaft is considered as a set of Timoshenko beam elements, and gyroscopic moment and centrifugal force are both considered. Adding bearing stiffness in the form of springs to this finite element system produced a spindle-bearing coupled model. Iteration was used to deduce the interactions among bearing groups. The exact whirl frequency of a spindle subjected to different pre-load mechanisms has been calculated. To validate the proposed theory, frequency analysis was carried out on a Siemens CAT40 spindle. Experimental results agreed with theoretical calculations. The result shows that speed had a great influence on bearing stiffness and spindle whirl frequency. Adopting a reasonable pre-load method and pre-load force improved the spindle critical frequency.
1. Introduction
As the speed and precision requirements increase, the key technologies of CNC machines tools and their main components have attracted increasing research attention. High speed spindles, as a key component of machine tools with rotational speeds greater than 100,000 rpm, present significant challenges for research into their dynamic characteristics. To predict and control the spindle dynamic performance (i.e. natural frequency, critical frequency, whirl and frequency), the relationship between bearing pre-load mechanism and spindle dynamic parameters should be ascertained: for this, an accurate spindle–bearing system coupled model is required.
However, the stiffness of a bearing varies at high speed and they interact with each other to provide a decisive impact on spindle system natural frequency. Under the action of unbalanced, gyroscopic moment, whirling arises as an intrinsic characteristic of rotating machinery. At high speed, the natural frequency is actually a whirl frequency. The point at which whirl frequency is equal to rotational frequency is the critical frequency of the spindle. Therefore, traditional models are no longer suitable for accurate calculation of high spindle whirl frequency.
The spindle system and its components have been widely studied. Liao et al. [1, 2] calculated bearing parameters using geometric analysis and force equilibrium analysis. Cao et al. [3-5] proposed a general modelling method for spindle systems comprising angular contact ball bearings, and a housing modelled with a standard non-linear bearing model and by treating the spindle as a set of Timoshenko beam elements. Bai et al. [6] analysed the influence of an axial pre-load force on the spindle, while Guo et al. [4-12] researched bearing behaviour by using a contact finite element model to obtain multi-group bearing stiffnesses. However, these studies focus on single-bearing modelling and calculate the stiffness; they pay less attention to the analysis of the pre-load mechanism in such systems.
Jedrzejewski [13-16] proposed a modelling method for a constant pressure bearing. Cao et al. investigated the rigid pre-load and constant pre-load mechanisms of angular contact ball bearings, and analysed the influence of different pre-load mechanisms on a spindle system in 2011. Gunduz [17-20] studied the influence of pre-load force on a spindle-bearing system equipped with a double row angular contact ball bearing. However, this research rarely modelled the same spindle equipped with bearings under different pre-load methods: thus they failed to analyse the interactions between bearing components adequately.
The arrangement and the pre-load methods for bearings, and selection of its pre-load force, are regarded as core technology in the design of spindle systems. The increase of pre-load force improves the support stiffness of the spindle system, but increases the contact load and heat generation therein. This reduces the fatigue life of a bearing. Besides, interactions among bearing components restricts the increment of the critical frequency of a spindle system. Thus, it was necessary to investigate the effect of bearing pre-load methods on the critical frequency and upon the interactions between its bearings.
This research revealed the relationship between pre-loading and whirl frequency of a spindle, and focussed on the interactions between bearing groups. A numerical analysis method based on a coupling spindle-bearing model was proposed. Two numerical models of the angular contact ball bearings based on rigid and constant pre-load mechanisms were established. The bearing support stiffness as modelled by spring elements and the bearing stiffness matrix was substituted into a spindle Timoshenko beam model using the finite element method. Applying pre-load and speed, the stiffness of bearings under specific working conditions was obtained by iteration. Subsequently, the whirl frequency was calculated. Lastly, the system model was validated by measuring the frequencies of an unloaded Siemens CAT40 spindle on which the pre-load forces and speed can be altered.
2. Dynamic model of the spindle and its bearing system
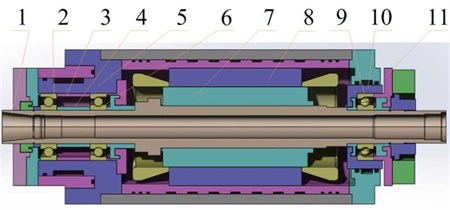
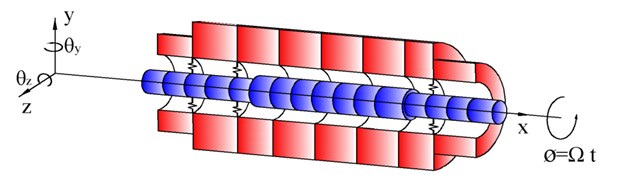
A Siemens CAT40 spindle system is shown in Fig. 1. Two groups of angular contact ball bearings are distributed on the two ends of the spindle system. The rigid pre-load bearing group at the front-end consists of bearings I and II arranged back-to-back. The length differences of the sleeves in its inner and outer rings are adjusted to realise the required pre-load. The length of the sleeve in the outer ring is greater than that in the inner ring. In motion, the outer ring and the spindle system housing are consolidated; the inner ring and shaft are also consolidated. Constant pre-load bearing III is fitted to the back-end of the spindle system. The disk spring applies a constant axial thrust (the pre-load) to the bearing, when there is thermal elongation of the spindle system; the sliding sleeve was consolidated with the bearing outer rings to allow axial sliding, so as to compensate for any thermal displacement. The axial pre-loads on the outer and inner rings of the bearing are constant.
Fig. 1System structure: the high-speed spindles 1. Bearing 1; 2. Sleeve of inner ring; 3. Sleeve of outer ring; 4. Bearing 2; 5. Spindle; 6. Motor rotor; 7. Motor stator; 8. Sliding sleeve; 9. Bearing 3; 10. Sliding zone of sliding sleeve; 11. Disk spring
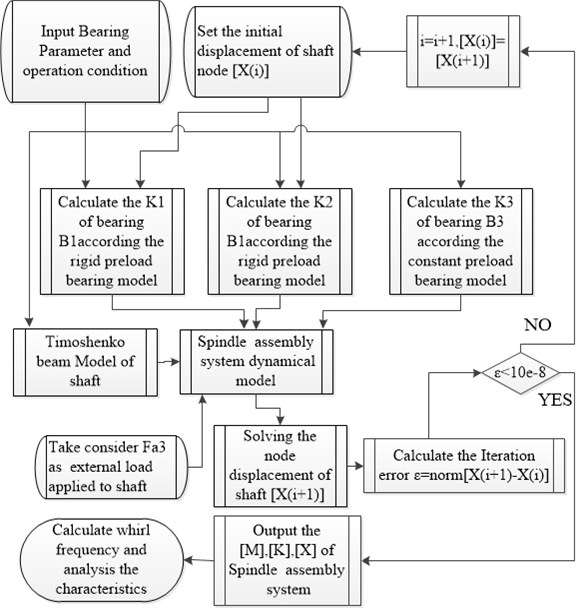
The coupling relationships among each sub-models of the high-speed spindle system are shown in Fig. 2. Based on the interactions between bearing groups with different pre-load mechanisms, the dynamic performance of a high-speed spindle system was investigated by using a spindle finite element model coupled with each sub-model.
Fig. 2Program flowchart for the spindle-bearing system analysis
2.1. Rigid pre-load bearing model
According to Hertzian contact theory, the relationship of the inner and outer rings of a bearing with the load deformation of the th rolling element is presented [21] as:
where, and are contact loads on the inner and outer rings respectively; and are the contact coefficients of the inner and outer rings; while and denote the contact loads on the inner and outer rings.
Based on the model proposed by Jones [22], the centripetal force and gyroscopic moment of a single rolling element are:
In Eq. (2), is the mass of a single rolling element; is the pitch diameter of the bearing; is the rotational inertia of a single rolling element; is the rotational speed of the spindle (rad/s); is the spinning angular speed of the rolling element (rad/s); is the angular speed of the rolling element rotating around the bearing centre; and is the angle between the spinning axis and the spindle of the rolling element.
The force balancing equation of the th rolling element is expressed [3] as:
where, and are the contact angles of the inner and outer rings respectively; and is the diameter of the rolling element. The rigid pre-load mechanism implied that a set of inner and outer rings of the bearing are consolidated with the spindle housing. By adjusting the size of the sleeve, the pre-load could be adjusted. Fig. 3 shows the relationship of pre-load to displacement during operation. The coordinate system [3] and geometry of Fig. 3 were used.
Fig. 3Rigid pre-load bearing geometry model
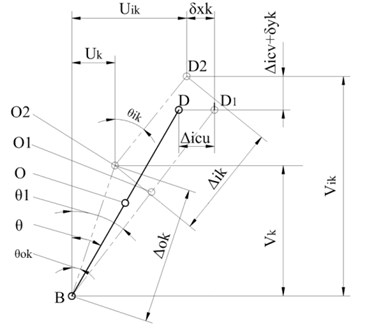
In Fig. 3, B is the centre of curvature of the outer ring of the bearing; D is the centre of curvature of the inner ring of the bearing; and O is the centre of curvature of the rolling element. In the absence of a pre-load, B, O, and D are collinear and angle between the vertical and the spindle is the initial contact angle of the bearing. With a pre-load, with the centre of curvature of the outer ring of the bearing B being constant, while that of the inner ring of the bearing D moves to D1 by amount , the axial rigid pre-load. Meanwhile, the centre of curvature of the rolling element moves from O to O1. In static conditions, B, O1, and D1 are still collinear, while the contact angle between the inner and outer rings increases to . During rotation, the centre of curvature of the rolling element moves from O2 to O1 influenced by centripetal force, gyroscopic moment, and external load. When in motion, the force on the back bearing and spindle pulls the centre of curvature of the inner ring of the bearing to D2 as found by iteration. This is the greatest difference between this study of rigid bearings and traditional models. As for the th rolling element, the geometric centre of curvature of the inner ring has displacements and in the horizontal and vertical directions respectively. Simultaneously, the contact angle of the inner ring increases, while the contact angle of the outer ring decreases. According to the geometry:
where:
Meanwhile, in accordance with the geometric relationships, Eq. (7) may be obtained:
where:
In Eqs. (5) to (11), and are coefficients for the inner and outer rings of the bearing respectively; is the phase angle of the th rolling element; , , , , and are the displacements generated by the pre-load; only when the pre-load is axial, , , , and are zero; , , , , and are the displacements induced by the inertial force and load.
By substituting Eqs. (6) to (10) into Eq. (5) separately, the geometric compatibility equation for the rigid pre-load bearing is established; by substituting Eqs. (1) to (3) into Eq. (4) separately gives the force balance equation. The dynamic contact angle , , , and of the inner and outer rings of the bearing are set as independent variables. Then the non-linear model for a rigid bearing is obtained by combining Eq. (4) with Eq. (5):
If , , , , , and , , , , and are known, the dynamic parameters of the bearing , , , and are found by Newton-Simpson iteration. However, since the displacements , , , , and are unknown when establishing a single bearing model, it is necessary to develop the spindle-bearing system model. Then the displacements induced by load can be determined iteratively. In turn, the dynamic parameters of the bearing may be found and the supporting stiffness of the bearing determined.
2.2. The constant pre-load bearing model
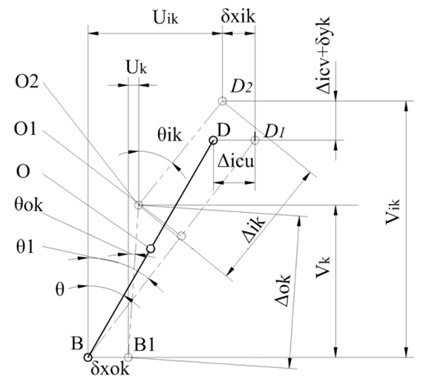
The mechanism of the constant pre-load bearing model is such that the inner ring of the bearing is consolidated with its spindle, while a disk spring applies a constant axial pressure to the outer ring. As the spindle undergoes thermal extension, the sliding sleeve connected to the outer ring of the bearing produces axial displacement. The load-deformation relationship and the force balance on the inner and outer rings with the rolling element are consistent with those for a rigid pre-loaded bearing. Fig. 4 shows the displacement relationship. According to the pre-load mechanism, a supplementary force balance equation can be obtained:
where, is the constant pre-load force.
The geometric relationship of the pre-loading process in a constant pre-load bearing is identical to that of the constant pre-load bearing. Under the effects of external load, inertial force, and thermal effects on the spindle, the centre of curvature of the inner and outer rings of the bearing would produce relative displacements. Under thermal effects, the centre of curvature of the inner ring moves from B to B1, while that of the outer ring migrates from D1 to D2. In the modelling process of a single bearing, it is difficult to determine the axial displacement of the inner ring of the bearing induced by thermal expansion; however, the displacement coordination system of Eq. (5) that is similar to that of the rigid pre-load method and can be established longitudinally. Similarly, by setting the dynamic contact angles of the inner and outer rings of the bearing , , , and as dependent variables and combining Eq. (4) with Eq. (5), the non-linear model for a constant-pressure bearing is established:
The symbols in Eq. (14) have the same meanings as those in Eq. (12). Similarly, if , , , , , and , , , , and are known, the dynamic parameters , , , and of the bearing may be found by Newton-Simpson iteration.
Fig. 4Constant pre-load geometry model
2.3. The stiffness matrix of the bearing
When the dynamic parameters: , , , and of the bearings are obtained, the stiffness matrix of the bearing can be found according to the model established by Cao. The calculation process is shown as Eqs. (40) and (41) and in [3], Appendix C. By calculation, the stiffness matrix of the bearing may be found.
2.4. The spindle-bearing system model
Fig. 5 shows the finite element model of the spindle-bearing system. The spindle is treated as a Timoshenko beam with five degrees of freedom. By applying the bearing stiffness at the corresponding nodes, the kinematic equation is obtained [3, 23]:
where, is the nodal mass matrix; is the mass matrix related to the centripetal force; is the mass matrix related to the gyroscopic couple; is the stiffness matrix of the beam; is a mass matrix induced by the axial force; is the nodal load matrix; is the rotation speed of the principal spindle; and is the nodal displacement vector. In the iteration process, the nodal displacement vector is used as the iterative object. The iteration process went as follows: firstly, the initial value is set and the stiffness of the bearing is calculated; afterwards, the stiffness obtained is substituted into Eq. (5) to yield the initial overall model; subsequently, the pre-load force and external load on the bearing are used as the load matrix to solve for the nodal displacements in the system; and then is calculated. If is smaller than the designed tolerance on numerical accuracy, the calculation is terminated; otherwise, is substituted into the bearing model to recalculate the bearing stiffness ( is the convergence coefficient: to guarantee convergence, Using this method, the iteration repeats until ; finally, the values of are substituted into the sub-models to obtain the system dynamic parameters.
Fig. 5Spindle system finite element model
After obtaining the system parameters, Eq. (15) is adjusted to:
where, , , and .
2.5. The whirling frequency of the spindle system
The spindle undergoes simple harmonic motion at a frequency of in the two mutually perpendicular directions. Generally, the amplitudes in the two directions are unequal. Since the locus of the circle’s centre of the motion is an ellipse, the motion is called a whirl or a precession. The natural frequency is the precession angular velocity. It is assumed that the spindle rotates at speed and whirls at frequency . Thus the spindle rotates in the bending plane of its axis and the shaft undergoes cyclic tension and compression. As a result, the internal resistance of the material influences the motions of the rotating parts and the fatigue life of the material. Only when , can the spindle avoid relative bending and develop synchronous whirl. Therefore, the whirl analysis of the spindle lays a basis for the selection of the bearing material, fatigue-based analysis of the spindle, and the selection of a reasonable working rotation speed.
When matrix , related to the gyroscopic couple, is taken into consideration, the principal spindle model should be converted to get the eigenvalue of the kinematic equation. Let:
where, is a state vector. Eq. (21) can be expressed as:
where:
is a -order unit matrix ; is the node number within the finite element model; and is the number of degrees of freedom of a single node.
The eigenvalue of matrix is the whirl frequency of the system. Through transformation, the system contains first-order differential equations. Since matrix , matrix is also antisymmetric.
Since , a couple of conjugate pure imaginary and are the eigenvalues of the system.
3. Experimental verification
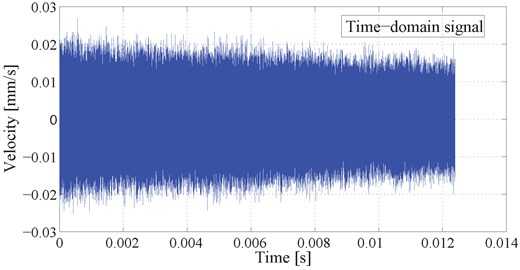
To validate the model, a frequency analysis was conducted using impulse analysis [24]. The spindle was excited using an impulse hammer and a laser velocity vibrometer was aimed at the front-end of the shaft to analyse data ultimately collected by an LMS collection and data analysis system. The sample frequency was 2,048 Hz. The front-end rigid pre-load on the spindle system was set to 3.6×10-5 m, while the back-end constant pre-load was set to 1,000 N. The experimental system is shown in Fig. 6. The time-domain signal and frequency domain data for a typical spindle (at 18,000 rpm) are shown in Fig. 7. The first-order frequencies were measured during rotation and key data are shown in Fig. 9 which fully validated the accuracy of the model.
This study investigated the dynamic characteristics of the unloaded spindle system: in real cutting processes, the spindle first-order frequency is slightly lower than its theoretical value. Since the multiple junction surfaces reduce the stiffness of the system, the cutting load may replicate the pre-loaded state of the spindle system.
The Siemens CAT40 spindle bearing is a type of hybrid ceramic angular contact ball bearing system. The inner and outer rings are made of alloy steel, while the rolling body is made of Si3N4 ceramic (type 7012C/H). Table 1 shows the main parameters of the bearing. The bearings are numbered (I, II, and III from front to back, respectively). The spindle is a hollow stepped spindle with an inner hole of diameter 42 mm. Table 2 lists the dimensions of the spindle.
Table 1Bearing geometry parameters
Item | Symbol | Size |
Ball diameter | /mm | 15.875 |
Number of balls | 14 | |
Curvature radius coefficient of inner ring raceway | 0.523 | |
Curvature radius coefficient of outer ring raceway | 0.525 | |
Initial contact angle | / (°) | 15 |
Bearing pitch circle diameter | /mm | 85.7505 |
Table 2Spindle dimension parameters
Spindle segment | Outer diameter / mm | Inner diameter / mm |
60 | 42 | |
90 | 42 | |
76 | 42 | |
58 | 42 |
Fig. 6Spindle testing: the experimental equipment

Fig. 7The time-domain signal and frequency domain data for a typical spindle (at 18,000 rpm)
4. Analysis of the whirl frequency under mixed pre-load mechanisms
4.1. Analysis of bearing stiffness
The support system was analysed under three working conditions:
1. Keeps a constant force on the pre-load bearing (bearing III). While setting the pre-load distance (the sleeve length difference between bearings I and II) on the rigid pre-load bearing to 1.29×10-5 m, 2.02×10-5 m, 2.6×10-5 m, and 3.1×10-5 m, respectively, and setting the rotation speed to zero.
2. Keeps the pre-load distance on the rigid pre-load bearings (bearings I and II) on the front end at 3.56×10-5 m. While setting the pre-load force of the constant pre-load bearing (bearing III) to 200 N, 400 N, 600 N, and 800 N respectively. The rotation speed was zero.
3. Keeps the pre-load distance on the rigid pre-load bearing group (bearings I and II) at 3.56×10-5 m. Uses a 1,000 N pre-load force on the constant pre-load bearing (bearing III) while setting the rotation speed to 5,000, 10,000, 15,000, 20,000, and 25,000 rpm respectively.
To assess the extent and effects of the interactions between bearing components, the elastic spindle and the bearing model are coupled to establish a force-displacement relationship for simultaneous solution. Fig. 2 illustrates the calculation process. Fig. 8 shows the stiffness of the bearing with an increase in the rigid pre-load distance (working condition 1). The stiffness of bearings I and II were increased. Moreover, the stiffness of bearing I exceeded that of bearing II due to the influence of bearing III’s pre-load force. This resulted in a pre-load force increase on bearing I, and diminished the pre-load force on bearing II. However, as the pre-load distance increased, the stiffness difference between bearings I and II gradually decreased. As the pre-load distance reached 3.56×10-5 m, the difference reduced to 2 %. Therefore, it can be deduced that, to prevent bearing II’s detachment a large pre-load distance from the rigid pre-load bearing should be selected. However, an overly high pre-load may induce sticking as it increases the contact load on the bearings and intensifies the friction between rolling elements and bearing rings.
Under working condition 1, the rotation of the spindle was zero, and the pre-load force on bearing III was constant. As the spindle generates displacement, the sleeve of the outer ring also shows a corresponding displacement. Therefore, the stiffness of bearing III remained constant.
Fig. 8Bearing stiffness for working condition set 1
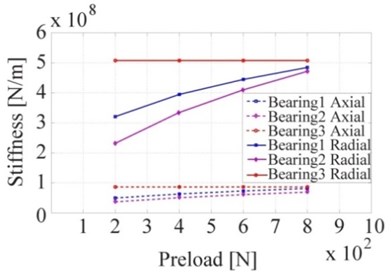
Fig. 9Bearing stiffness for the second set of working conditions
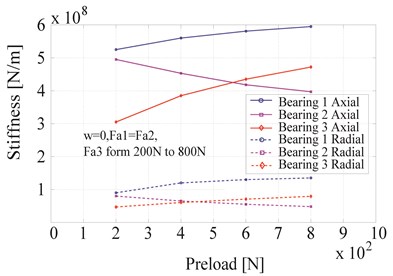
Fig. 10Bearing stiffness for the third set of working conditions
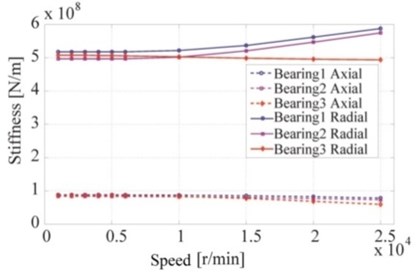
Fig. 9 shows the stiffness of each bearing under working condition set 2. In the case of applying a low pre-load to the constant-pressure bearing at the rear end, bearings I and II show only a small stiffness difference. As the pre-load force increases on bearing III, the stiffness thereof also increases; the stiffness difference between bearings I and II increases significantly; the stiffness of bearing I increased and the stiffness of bearing II decreased. Therefore, it can be seen that, as the pre-load force increased it could enhance the supports stiffness of the spindle back-end while generating a significant stiffness difference in the rigid pre-load bearing group.
Static analysis of the two sets of working conditions suggested that, the pre-load state of the rigid pre-load bearing had no influence on the constant pre-load bearing, whereas the pre-load on the back-bearing exerted a significant influence on the front rigid pre-load bearing group.
Fig. 10 shows the influence of both the centripetal force and gyroscopic moment on the pre-loaded bearings under operating conditions. Analysis of the results reveals that, with an increased spindle rotation speed, the rigid pre-load bearings I and II underwent an increase in stiffness while the constant pre-load bearing showed a concomitant stiffness reduction. As the rotation speed increased from 5,000 rpm to 25,000 rpm, the stiffness increased by 19.6 % (Bearing I) and 18.8 % (Bearing II) respectively. This stiffness increase was mainly attributed to the contact load increase on the rolling elements and bearing rings. Meanwhile, the stiffness of the constant pre-load bearing at the rear end decreased by 5.3 % because of the inertial force increasing the load on the outer ring, while the displacement of the sleeve kept the load on the outer ring constant. The inertial force actually reduced the contact force between rollers and inner ring. Therefore, the stiffness of the constant pre-load bearing decreased under high-speed rotation. These results suggest that the rigid pre-loaded bearing unit installed on the front end of the high-speed spindle was more appropriate. It was more favourable to maintain the stiffness of the spindle system; the constant pre-load bearing installed on the rear end was more conducive to compensating for thermal extension of the spindle system.
4.2. Analysis of the frequency of the spindle system
Table 3 shows theoretical results for the spindle’s first-order natural frequencies. These could be validated by impact hammer test at a fixed pre-load distance of 3.56×10-5 m and a 1,000 N constant pre-load.
Table 3 shows that, when bearing III maintained its high pre-load level, the pre-load on the front bearings exerted little influence on the first-order fundamental frequency of the system. However, when keeping the rigid pre-load distance (bearings I and II) constant, the increase of pre-load (on bearing III) significantly increased the first-order natural frequency of the spindle system. Therefore, when designing the supporting system, the rear constant pre-load bearing should be subjected to a high pre-load.
Table 3Spindle system frequencies
Front-end pre-loading distance / 10-5 m | Back-end pre-load / N | First order frequency / Hz |
1.29 | 1000 | 382 |
2.02 | 1000 | 394 |
2.6 | 1000 | 396 |
3.1 | 1000 | 397 |
3.56 | 200 | 316 |
3.56 | 400 | 349 |
3.56 | 600 | 364 |
3.56 | 800 | 378 |
3.56 | 1000 | 398 |
Ignoring the gyroscopic moment, the natural frequency of spindle could be found. When running, the first-order frequency of the spindle was actually its whirl frequency. The point at which the whirl frequency was equal to the rotational frequency was the critical frequency of spindle. When researching the critical frequency speed of rotating systems, the emphasis is commonly put on investigating the critical speed of synchronous positive whirl. Under unbalanced excitation, the rotator whirls synchronously and positively. Hence, the critical rotation speed generally refers to the critical speed for synchronous positive whirl [10]. Under the effects of the inertial force of the spindle, the positive whirl frequency of the spindle increases, while its negative whirl frequency decreases (the speed becomes negative, i.e. it ceases to exist).
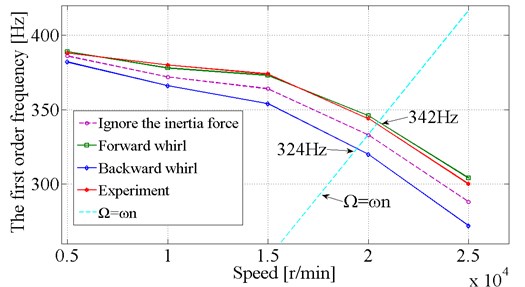
Fig. 11 shows the effects of inertial load and bearing stiffness on the frequency of the spindle. When running, the natural frequency of the spindle decreases significantly due to the rotation speed reduces the supporting stiffness of the constant pre-load bearing (Fig. 10).
As shown in Fig. 11, when neglecting the whirling effect of the spindle, the calculation error increases with speed. As the rotation speed reaches 25,000 rpm, the theoretical calculation error is 5.3 %. Nevertheless, this can be accepted in practical engineering circumstances, and was more accurate than traditional models. By drawing a straight line at in Fig. 11, the intersection point of this line with the positive whirl curve. It gives the critical frequency of the spindle system (at 342 Hz here). Therefore, it can be deduced that the first-order critical frequency of the spindle system occurs at 20,520 rpm under the given pre-load conditions. It was deduced that the Siemens CAT40 spindle cannot avoid the first-order critical frequency over its full operating speed domain as it was a flexible spindle.
Fig. 11Whirl frequency of the spindle system
5. Conclusions
1) This study reveals the relationship between pre-loading and whirl frequency of a spindle. Research shows that the bearing stiffness varies at high speed and interacts with that of other components of the system. Its most decisive impact lay upon the spindle system natural frequency while also influencing the whirl frequency, albeit indirectly. The stiffness of the constant pre-load bearing decreased, as the spindle natural frequency decreased: the whirl frequency also decreased, which therefore reduced the first-order frequency.
2) This study presented an integrated bearing-shaft coupled model. Two numerical bearing models, based on the Harris bearing model, were established for different pre-load mechanisms. Considering the shaft and housing as Timoshenko beam elements, we modelled the bearing stiffness matrix for the shaft and housing by the finite element method and obtained the bearing stiffness by iteration. The interaction of the bearings under inertial force and pre-load force were analysed. The proposed theory was validated by frequency test. This model can be used to predict spindle natural frequencies, whirl frequencies, and critical frequencies with acceptable accuracy.
3) In engineering, it is suggested that it is advisable to arrange a rigid pre-load bearing group in front of the spindle to maintain system stiffness. To increase the critical frequency of a spindle, an effective method was to apply a significant pre-load force to the constant pre-load bearing. However, this will increase the stiffness difference so, pre-load forces should be optimised at the design stage for such high speed spindles.
References
-
Liao N. T., Lin J. F. Ball bearing skidding under radial and axial loads. Mechanism and Machine Theory, Vol. 37, Issue 2, 2002, p. 91-113.
-
Liao N. T., Lin J. F. An analysis of misaligned single-row angular-contact ball bearing. Journal of Mechanical Design, Vol. 126, 2004, p. 370-374.
-
Cao Y. Z., Altintas Y. A general method for the modeling of spindle-bearing systems. Journal of Mechanical Design, Vol. 126, Issue 6, 2004, p. 1089-1104.
-
Cao Y. Z., Altintas Y. Modeling of spindle-bearing and machine tool systems for virtual simulation of milling operations. International Journal of Machine Tools & Manufacture, Vol. 47, 2007, p. 1342-1350.
-
Maeda O., Cao, Y. Z., Altintas Y. Expert spindle design system. International Journal of Machine Tools & Manufacture, Vol. 45, 2005, p. 537-548.
-
Bai C. Q., Zhang H. Y., Xu Q. Y. Effects of axial pre-load of ball bearing on the nonlinear dynamic characteristics of a rotor-bearing system. Nonlinear Dynamics, Vol. 53, 2008, p. 173-190.
-
Guo Y., Parker R. G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model. Mechanism and Machine Theory, Vol. 51, Issue 40, 2012, p. 32-45.
-
Parker R. G., Mote C. J. Vibration and coupling phenomena in asymmetric disk-spindle systems. Journal of Applied Mechanics, Transactions of the ASME, Vol. 63, 1996, p. 953-961.
-
Parker R. G. Analytical vibration of spinning, elastic disk-spindle systems. Journal of Applied Mechanics, Transactions of the ASME, Vol. 66, 1999, p. 218-224.
-
Parker R. G., Sathe P. J. Free vibration and stability of a spinning disk-spindle system. Journal of Vibration and Accoustics, Transactions of the ASME, Vol. 121, 1999, p. 391-396.
-
Parker R. G., Sathe P. J. Exact solutions for the free and forced vibration of a rotating disk-spindle system. Journal of Sound and Vibration, Vol. 223, 1999, p. 445-465.
-
Guo Y., Parker R. G. Dynamic modeling and analysis of a planetary gear involving tooth wedging and bearing clearance nonlinearity. Proceedings of the ASME International Design Engineering Technical Conferences/Computers and Information in Engineering Conference, 2010, p. 217-231.
-
Jedrzejewski J., Kwasny W. Modelling of angular contact ball bearings and axial displacements for high-speed spindles. Cirp Annals Manufacturing Technology, Vol. 59, Issue 2, 2010, p. 377-382.
-
Jedrzejewski J., Kowal Z., Kwasny W., Modrzycki W. High-speed precise machine tools spindle units improving. Journal of Materials Processing Technology, Vol. 162, 2010, p. 615-621.
-
Jedrzejewski J., Kowal Z., Kwasny W., Modrzycki W. Hybrid model of high speed machining centre headstock. Cirp Annals-Manufacturing Technology, Vol. 53, 2004, p. 285-288.
-
Jedrzejewski J. Effect of the thermal contact resistance on thermal-behavior of the spindle radial-bearings. International Journal of Machine Tools & Manufacture, Vol. 28, 1998, p. 409-416.
-
Gunduz A., Dreyer J. T., Singh R. Effect of bearing pre-loads on the modal characteristics of a shaft-bearing assembly: Experiments on double row angular contact ball bearings. Mechanical Systems and Signal Processing, Vol. 31, Issue 6, 2012, p. 176-195.
-
Sirohi S. C., Prakash S., Rana P., Singh R. Response of mango malformation to severity of malformed panicle bearing shoot pruning. Indian Journal of Horticulture, Vol. 66, 2009, p. 393-395.
-
Kim S., Singh R. Vibration transmission through an isolator modelled by continuous system theory. Journal of Sound and Vibration, Vol. 248, 2001, p. 925-953.
-
Lim T. C., Singh R. Vibration transmission through rolling element bearings, Part 1. Bearing stiffness formulation. Journal of Sound and Vibration, Vol. 139, 1990, p. 179-199.
-
Harris T. A. Rolling Bearing Analysis, 4th Ed. Wiley, New York, 2001.
-
Jones A. B. A General theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions. Journal of Basic Engineering, Vol. 25, Issue 9, 1960, p. 309-320.
-
Cai Li-gang, Ma Shi-ming, Zhao Yong-sheng, et al. Finite element modelling and modal analysis of heavy-duty mechanical spindle under multiple constraints. Journal of Mechanical Engineering, Vol. 3, 2012, p. 169-177, (in Chinese).
-
Jorgensen B. R., Shin Y. C. Dynamics of spindle-bearing systems at high speeds including cutting load effects. ASME Journal of Manufacturing Science and Engineering, Vol. 120, Issue 2, 1998, p. 387-394.
About this article
The authors thank the reviewers for their valuable comments and suggestions. This work was supported by the National High-tech R&D Programme (863 Programme): Design and Manufacturing Technology of Precise Horizontal Machining Centre (Grant No. SS2012AA040702) and The Major Specialised Science and Technology Programme: Innovation Ability Platform for Precise and Ultra-Precise NC Machine Tools (Grant No. 2011ZX04016-011).
