Cast partials analysis using a proprietary test station

1. Introduction

Many companies and institutes, both domestic and foreign, conduct research into mathematical modelling of dental prostheses (including implants). Institute of Dentistry of Medical University of Warsaw is one of leading research facilities in that field. The scope of research is limited to static loads to which biomechanical prostheses are exposed. Institute of Electronic Systems under the Military University of Technology carried out a comprehensive mathematical evaluation and analysis of a dental prosthesis, both under static and kinematic loads [1, 2], factoring in the model of gum tissue.

Mathematical models of dental prostheses are very insightful and informative. They facilitate an end-to-end, holistic investigation (strain and stress) of every area of dental prosthesis under any external inputs [3]. Moreover, the durability of prosthesis during its typical lifecycle can be traced and assessed. Ultimately though, it is a tool difficult to develop, complicated and expensive. Hence it is unfit for common, day-to-day use by prosthetists.

Thankfully, it is possible to model kinematic inputs and response of gum soft tissue thus a virtual prosthesis is a feasible concept. It could be quickly and easily modified to replicate a particular dentition, allowing examining it. For this reason, kinematic modelling of dental prostheses is highly useful.

The frequency teeth are subject to loading during comminution of food is between 40-120 cycles/min [4, 5]. Effective static load applied to the occlusal surface (biting surface) does not exceed 20 N.

Preliminary tests and simulations using a flat prosthesis model prove that regardless of load application point, there is a linear relationship between deflection as well as deformation of prosthesis metal panel and loads not exceeding 15 N [6, 7].

Estimated deflections should not exceed 5 mm [8]. It is difficult, however, to make accurate projections of deflections occurring during testing, because they would vary depending on test points. Nevertheless, an assumption may be made that values of deflections should not exceed ±300 μm/m. Despite above assumptions regarding boundary test values, the measuring system was designed to enable broader measurement scope in order to test for external loads up to 20-25 N [2, 9].

2. Cast partials testing

Research effort was channelled into conducting a numerical analysis of cast partials under dynamie load. The specimen (Fig. 1) used for analysis was a replica of an intraoral prosthesis – a partial denture replacing six teeth and worn by a partially edentulous patient.

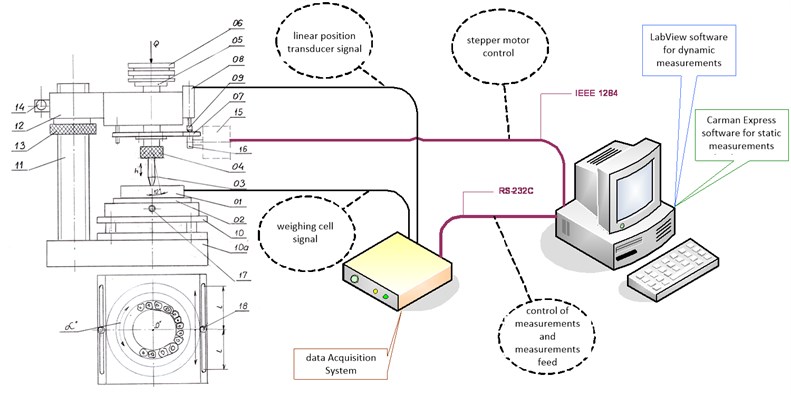
Fig. 2 illustrates a purpose-built test station designed to determine and measure model prosthesis’ responses to dynamic load. At the design stage, emphasis was put on facilitating carrying out diagnostic measurements [10] as well as reliability (that also meant taking into account electromagnetic interference [11, 12]) through putting in place adequate reliability structures [13, 14].

Fig. 1Test prosthesis with highlighted load application points (23-27)

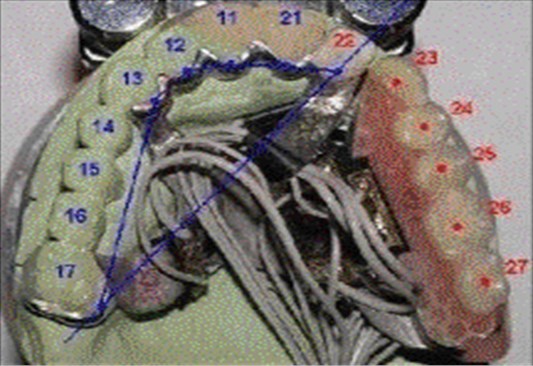
Fig. 2Diagram of test station

3. Dynamic test – basic assumptions

Because of theoretical complexity of the issue, especially a multitude of approaches developed over time, it became apparent a detailed description is required.

A dynamic analysis – for purposes of this paper - means solving a system in movement which changes in time (acceleration, deceleration) thus requires to include inertial forces in calculations.

A variable motion (oscillation) is considered against a static equilibrium reached through all the forces that act upon an object being balanced. The state where a structure is under maximum load results from constant static loads, exciting forces and maximum (amplitude) inertial forces of individual masses.

During taking measurements of the stress-strain relationship, the oscillatory motion around the static balance point. The scope of analysis was intentionally limited to describing distribution and size of loads as well as describing external applied forces (excitations) as space and time dependent.

4. Description of dynamic load

In order to unequivocally determine a dynamic load, it is necessary to determine application of force, direction of action and time variability.

Points of application of force and their interaction are usually determined using dynamic degrees of freedom. Their number initially equals local (static) degrees of freedom. As discretization progresses that number gets considerably reduced.

Oscillatory motion around neutral position occurs when a system is displaced from its equilibrium and deviates from it repetitively to a limited extent in certain time periods:

Notation (1) presents the periodic motion within period $T$. The repeating fragment of that activity within that period is referred to as a cycle.

Harmonic motion is a special case of periodic motion:

where: $a$ – amplitude $q$, $T$ – period [s], $\omega =2\pi /T$ – angular frequency, $\omega t+\phi$ – phase, $\phi$ initial phase.

The tests were carried out to observe influence of time-variant load $p\left(t\right)$ within time t on the structure (prosthesis). Applied force caused the prosthesis to bend.

The effects of applied dynamic load are qualitatively identical compared to static load, hence fully reliable for using in structural calculations. The only prerequisite is determining the so-called dynamic load factor (DLF). It defines the relationship between maximum strain caused by dynamic loads and those caused by a static load.

The unknown dynamic load could be determined as equivalent load by using the Hooke’s law whereby stress is proportional to strain:

The value of DLF could be determined analytically (by using e.g. the minimum eigenvalue) or empirically through an experiment by measuring structure's actual vibrations. It had been done for building structures and consequently standardised.

5. Conclusions

This paper discusses issues related to arch cast partials. Functional analysis of such prostheses was carried out, factoring in loads and strains to which they are exposed. Consequently a test station was designed for measuring model prosthesis strain under dynamic load. Lab-View software was used to control the stepper motor (over IEEE 1284 bus) and take measurements of weighing cell signals (over RS-232 bus). Tests results are then visualised on computer display and undergo statistical analysis using CatmanExpress software. Plans for further research include numerical analysis of the prosthesis using the Finite Element Method.