New dynamics concepts for vibration-based damage detection: wavelet modal curvatures

1. Introduction

Structural health monitoring and damage detection relying on vibration characteristics has been a research focus of increasing interest in various fields such as mechanical, civil, aerospace, and military, during the last few decades [1-2]. Among methods for vibration-based damage detection, modal curvature is a representative damage feature with frequently mentioned merits: (i) accurate indication of damage occurrence; (ii) instant determination of damage location, and (iii) no need for prior knowledge of damage. 1D and 2D modal curvatures have been widely applied to the identification of damage in beams [3-8] and plates [9-13] in relatively high signal-to-noise ratio (SNR) conditions. Despite its prevalence in portraying damage, modal curvature has the notable deficiency of susceptibility to measurement noise: when modal curvature is derived by second-order differentiation of a mode shape, the measurement noise involved in the mode shape can be considerably amplified by the differentiation, likely obscuring genuine damage characteristics and so frustrating damage identification. Some researchers [7-8] have devised strategies with the aim of overcoming this deficiency of modal curvature. Nevertheless, the majority of the developed methods rely on denoising, optimizing sampling interval, etc., without being able to solve the problem with solid theoretical and physical support. To address this problem, the group the author works in reforms the conventional modal curvature using wavelet transform techniques, producing a novel type of wavelet modal curvatures. Wavelet modal curvature enjoys the multiscale property of the wavelet transform in adaptability to noise, exhibiting distinctive advantages of robustness against noise in characterizing damage. In this study, wavelet modal curvatures developed in our group are briefly introduced and their capabilities to identify damage in noisy environments are demonstrated in experimental cases.

2. Conventional modal curvature

The modal curvature $\kappa \left(x\right)$ of a vibrating beam is defined by the second-order derivatives of a mode shape $W\left(x\right)$ [3]:

where $M\left(x\right)$ is the bending moment and $EI\left(x\right)$ is the flexural stiffness.

The modal curvature $\kappa (x,y)$ of a vibrating thin plate is defined by the 2D Laplacian of a mode shape $W(x,y)$:

where $D=E{h}^3/12(1-{\upsilon }^2)$ is the flexural rigidity with $E$ the Young’s modulus, $\upsilon$ the Poisson’s ratio, and $h$ the thickness of the plate; $M_x(x,y)$ and $M_y(x,y)$ are bending moments in the $x$ and $y$ directions.

Damage causes change in $EI\left(x\right)$ for beams or $D(x,y)$ for plates. The change entails discontinuity in $\kappa \left(x\right)$ or $\kappa (x,y)$ under the premise of continuity in bending moment. Discontinuity in the modal curvature manifests the occurrence, location, and even severity of damage. This theoretical observation lays the foundation for using modal curvature to identify damage.

The Fourier counterparts of modal curvatures, $\kappa \left(x\right)$ and $\kappa (x,y)$ are $\left(i\omega {)}^2\widehat{F}\right(\omega )$ and $\left((i{\omega }_x{)}^2+(i{\omega }_y{)}^2\right)\widehat{F}({\omega }_x,{\omega }_y)\text{,}$ respectively, where $\omega$ represents the angular frequency. The square of $\omega$, ${\omega }_x$ or ${\omega }_y$ in the Fourier counterpart necessarily enlarges the high-frequency contents in mode shapes. Owing to the fact that measurement noise is commonly of predominantly high-frequency components, these components are thereby favorably enlarged such that they likely dominate the modal curvature [7, 14].

3. Wavelet modal curvature

Wavelet modal curvature is formulated based on using a wavelet transform to expand a modal shape from a space domain to a space-scale domain [15], with accomplishment of the second-order differentiation function at the scale level.

1) 1D wavelet modal curvature: $W_s^{\mathrm{*}}\left(u\right)$ [16, 17]:

where $\otimes$ denotes the manipulation of convolution; ${\overline{\psi }}_s\left(x\right)=1/\sqrt{s}\psi \left(-x/s\right)$ at the scale $s$ is derived from the mother wavelet $\psi \left(x\right)$; $\psi \left(x\right)$ is specified by the second-order derivatives of the smooth function $\theta \left(x\right)$, typically the Gaussian function, for which ${\stackrel{-}{\theta }}_s\left(x\right)=1/\sqrt{s}\theta \left(-x/s\right)$; $u$ is the translation parameter.

2) 2D wavelet modal curvature: $W_s^{\mathrm{*}}(u,v)$ [17]:

where ${\overline{\psi }}_s(x,y)=1/s\psi (-x/s,-y/s)$ at the scale $s$ originates from the mother wavelet $\psi (x,y)$; $\psi (x,y)$ is defined by the second-order derivatives of the smooth function $\theta (x,y)$, for which ${\stackrel{-}{\theta }}_s(x,y)=1/s\theta (-x/s,-y/s)$; $u$ and $v$ are the translation parameters in the $x$ and $y$ directions, respectively.

In Eqs. (3) and (4), $W_s^{\mathrm{*}}\left(u\right)$ or $W_s^{\mathrm{*}}(u,v)$ is generated by second-order differentiation of a beam mode shape or a plate mode shape that is pre-smoothed by ${\stackrel{-}{\theta }}_s\left(x\right)$ and ${\stackrel{-}{\theta }}_s(x,y)$, respectively. The wavelet modal curvature inherits from the wavelet transform the multiscale property, which provides a distinctive mechanism of adaptability to noise [15-17].

For post-processing, the Teager energy operator (TEO), $y\left(x_i\right)=x_i^2-x_{i-1}{x}_{i+1}$, is generally employed to further treat the wavelet modal curvature with the aim of intensifying damage features [18, 19]:

where ${\mathrm{\Psi }}_s\left(W_s^{\mathrm{*}}\right[i\left]\right)$ is the 1D TEO-processed wavelet modal curvature for a beam and ${\mathrm{\Psi }}_s\left(W_s^{\mathrm{*}}\right[i,k\left]\right)$ is the 2D TEO-processed wavelet modal curvature for a plate.

3) Complex-wavelet modal curvature: $C{W}_s^{\mathrm{*}}\left(u\right)$ [20]:

A complex-wavelet modal curvature features both noise robustness and damage sensitivity [20], defined by:

where ${\overline{\psi }}_s\left(x\right)=1/\sqrt{s}\psi \left(-x/s\right)$ at the scale $s$ is derived from the complex mother wavelet $\psi \left(x\right)$; $\psi \left(x\right)$ is set by the second-order differentiation of the smooth complex function $\theta \left(x\right)$, for which ${\stackrel{-}{\theta }}_s\left(x\right)=1/\sqrt{s}\theta \left(-x/s\right)$; $u$ is the translation parameter. The complex-wavelet modal curvature consists of a pair of real and imaginary parts, their modulus designating damage.

4. Experimental validation

4.1. Wavelet modal curvature

1)$W_s^{*}\left(u\right)$ for detecting multiple cracks in aluminum beams.

An aluminum beam with three cracks is excited by an electromechanical shaker (Fig. 1) and its mode shapes are acquired by a scanning laser vibrometer (SLV) [21]. As illustrated by the 5th mode shape, the relevant 1D TEO-processed wavelet modal curvature is dominated by three singular peaks increasing with scale, and they clearly pinpoint the actual cracks (Fig. 2).

Fig. 1Alunimun beam with three cracks [17]

Fig. 21D TEO-processed Ws*(u) [17]

2) $C{W}_s^{\mathrm{*}}\left(u\right)$ for identifying multiple cracks in composite beams.

A carbon-fiber-reinforced polymer (CFRP) composite beam consisting of five layers is considered, in which three cracks are cut deep into the second layer (Fig. 3). An electromechanical shaker is used to excite the beam together with its mode shapes measured by a SLV. The 4th mode shape is arbitrarily selected to exemplify the method. In the complex-wavelet modal curvature, three peaks arising along scale clearly designate the genuine cracks (Fig. 4).

Fig. 3CFRP beam with a crack [20]

Fig. 4Complex-wavelet modal curvature [20]

3) $W_s^{\mathrm{*}}(u,v)$ for characterizing cross-like notch in aluminum plates.

An aluminum plate containing a cross-like notch, with its geometry shown in Fig. 5, is excited with a piezoelectric lead-zirconate-titanate (PZT) actuator. The mode shapes of the plate are obtained by using a SLV as a sensor. A distinct peak appearing in the 2D-TEO processed wavelet modal curvature (at scale 20) of the mode shape at the natural frequency of 3000 Hz clearly delineates the notch (Fig. 6).

Fig. 5Aluminum plate with a cross-like notch: a) geometry and b) zoomed-in notch [17]

Fig. 62D-TEO processed wavelet modal curvature: a) planform and b) enlarged damage [17]

4.2. Conventional modal curvature

The experimental cases above are reanalyzed by conventional modal curvatures, with the results shown in Figs. 7(a), 7(b), 7(c) for the aluminum beam, composite beam, aluminum plate, respectively. In these modal curvatures, the noise effect entirely impairs the modal curvatures, from which no damage feature is identifiable. Comparisons with the results from wavelet modal curvatures in Figs. 2, 4, 6 clearly illustrate the disadvantage of conventional modal curvature in resisting noise.

Fig. 7Modal curvatures for: a) aluminum beam, b) composite beam, and c) aluminum plate

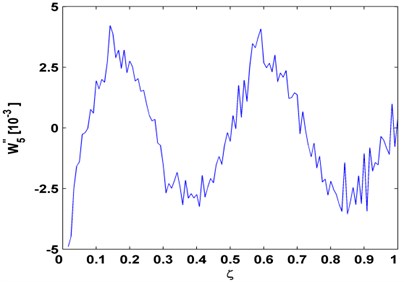
a)

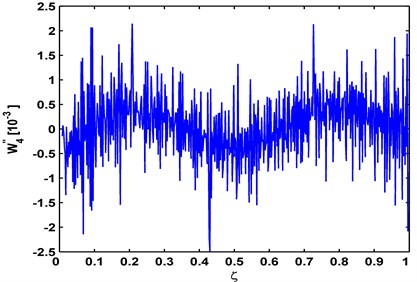
b)

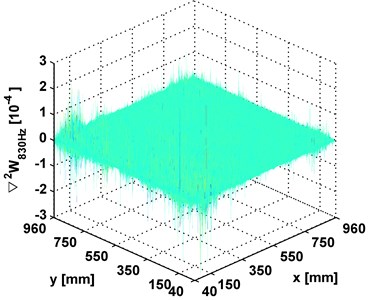
c)

5. Conclusions

Modal curvature is a widely used damage indicator with explicit physical implication; however, its noise susceptibility compromises its effectiveness in characterizing damage in noisy conditions. This study reports new concepts of wavelet modal curvatures that has superiority over conventional modal curvature in the mechanism of adaptability to noise. The capabilities of wavelet modal curvatures to detect complex damage in noisy environments are demonstrated in experimental cases.