Machine vibrations analysis working in non-stationary states

1. Introduction

The diagnosing of rotor machine state in alternating conditions in real time is vital for their operation safety. Early detection of the conditions of incorrect operational processes as well as arising damages development can often prevent from failures, or serious accidents. However, diagnostics during variable operational conditions of the object based on residual processes causes real difficulties in effective, yet simple diagnostic symptoms synthesis [1, 2]. The application of synchronic selection gives the possibility of increasing the energy contributions of time- and frequency-symptomatic components of the signal [3-5]. However, the characteristics based on Fourier’s transformation, as long as they are only the function of frequency, well describe the signal’s variations, on condition that the signal is stationary [6]. This characteristic seems to be obvious, yet it is often forgotten in engineering practice. In recent years methods describing signal’s variations in time and frequency simultaneously have become the brilliant solution of this problem. However, time-frequency methods are very time-consuming. So for the enhancement of diagnostic symptoms selectivity at variable rotation speeds the method of transformation of dynamic time scale into cycle scale has been introduced by the authors of this article [7, 8]. The final product was the signal spectrum for which the symptomatic components are synchronic to the rotation speed in the specific observation window time.

Diagnosing rotary-machine states in variable real-time conditions is vital for their operational safety. Early detection of conditions of incorrect operational processes, as well as arising damage development can often prevent from failures or industrial accidents. The Procedure of Linear Decimation (PLD) [5, 8] has been successfully tested in diagnostic systems for non-stationary cyclical machines. Application PLD offers the possibility to increase the energy contributions of time- and frequency- symptomatic components of the signal.

2. Procedure of linear decimation (PLD)

Procedure of Linear Decimation involves the dynamic signal resampling in accordance with rotation speed variations [7]. It assumes linear approximation of cycle variations curbed by values representing its beginning cycle time ${\mathrm{\Theta }}_p$ and its end cycle time ${\mathrm{\Theta }}_k$. In other words, it involves the deletion of sample-cluster variations proportional to the cycle and maintaining the constant sample-per-cycle number.

The key element is to define decimation coefficient $D{c}_K$. This coefficient characterizes the increment of signal resampling [5]. It changes in accordance with the increase or decrease of the rotation speed, i.e. with the cycle variations. By adapting the final decimation coefficient we can determine its variations in accordance with linear signal trend. Selecting final decimation coefficient enables to reduce the signal to the stationary form in the observation window for the last cycle, which is very convenient in real-time analysis. Developed method was meticulously tested on non-stationary signals recorded on various types of rotary machines. Simple in implementing, yielding positive results, with presence of linear cycle trend

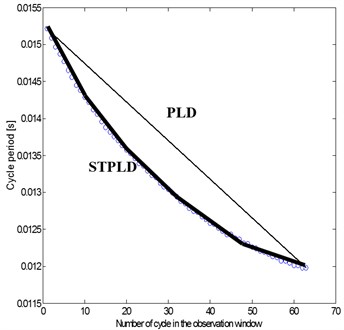
Fig. 1. Approximation of cycle change in observation window with PLD and STPLD

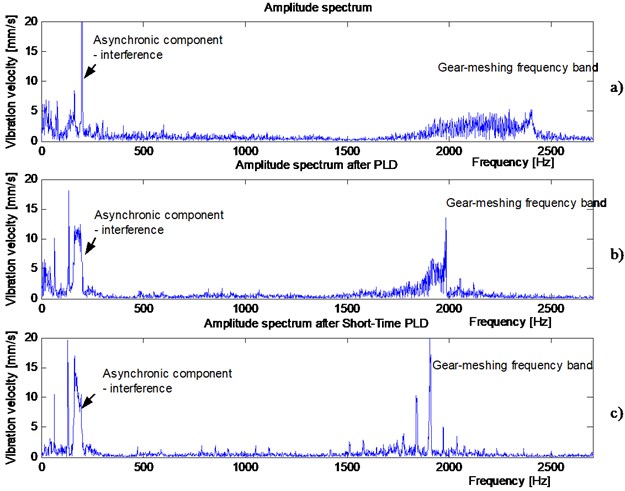
Fig. 2Amplitude spectrum of vibration velocity of gear meshing resulted after applying PLD and Short-Time PLD. Average rotational speed increase – 0.38 % per cycle

3. Short-time procedure of linear decimation

As for rotary machines at the stage of run-up, particularly machines of dynamic changes of rotation speed, preserving linearity did not significantly improve spectral selectivity, especially in high-frequency band Fig. 2(b). This prompted developing modified algorithm of the method enabling adjustment to cycle change in short time-periods of an observation window. The new method of analyzing signals in narrow time-periods was referred to as Short-time Procedure of Linear Decimation STPLD [8]. Its algorithm is presented in article [3]. Fig. 1 presents schematically the adjustment of linear approximation to cycle changes in observation window.

STPLD method was tested in high-frequency bands. Results obtained during examining signals in gear-meshing frequency band were very satisfactory, as presented in Fig. 2(c).

The hardware implementation in FPGA (Field Programmable Gate Arrays) of the PLD significantly shortens computation time and allows increasing signal sampling frequency [8]. Enabled device hardware solution denoted as Programmable Unit for Diagnostic (PUD-2) based on Filed Programmable Gate Arrays (FPGAs) and ARM-based OMAP3530 microprocessor adapted for diagnostic systems [9]. The sampling frequency of the input analog signals and digital signals processing speed of the PUD is high beyond comparable DSP [10, 11].

4. Conclusions

Hardware realisation of linear decimation procedure based on FPGA programmable systems provides the possibility of diagnosing cyclical machines at variable operating conditions in real time.

A Short-Time PLD method was developed, enabling to adapt the approximation to the cycle changes. This methods averts the problem of non-linear trend change and minimizes the error resulted from the original PLD assumption of linear cycle trend in the observation window.