Fault diagnosis for the gearbox of wind turbine combining ensemble intrinsic time-scale decomposition with Wigner bi-spectrum entropy

1. Introduction

In recent years, with the continuous need for renewable energy, wind energy has been greatly developed. In the meantime, due to poor operating conditions, the failure rate of the key components of the wind turbine is greatly improved [1, 2]. The main faults of wind turbine include of transmitting system faults [3], blade pitch faults [4], and rolling bearing faults [5]. The gearbox is one of important parts of the wind turbine. The faults of gearbox will unavoidably result in the system to stop working. It has always been being a difficult problem in the fault diagnosis how to extract fault feature information effectively and accurately from the vibration signals. The conventional feature extraction indicator in fault diagnosis of wind turbine gearbox can be concluded as Power spectrum entropy [6], Wavelet energy entropy [7] and Morphological Operators [8]. These methods analyze the fault vibration signal in time or frequency domain, so as to identify the working condition of wind turbine gearbox. However, because of the various effect of nonlinear factors, i.e. friction, clearance, stiffness and load to vibration signals, it is not easy to accurately recognize the fault type of wind turbine gearbox when the working condition of wind turbine gearbox is analyzed only in time domain or frequency domain. Hence, it is very necessary to develop feature extraction method to effectively recognize the working state and fault types of wind turbine gearbox.

Currently, there are a lot of time-frequency analysis methods on fault diagnosis in wind turbine gearbox, including of wavelet transform (WT) [9], empirical mode decomposition (EMD) [10], and local mean decomposition (LMD) [11]. But the related studies have shown that these methods have some limitations for non-stationary frequency-modulated and amplitude-modulated signals and the practical vibration signal [12]. For example, WT needs selecting the appropriate wavelet basis function and decomposing layers to analysis the vibration signal, that is to say it is lack of adaptability for signal processing. EMD method has the drawback of envelope overshoot or shortage, mode mixing, end effect, etc. As an improvement of EMD, LMD method also possesses the problems of more iterative calculation, distorted components, mode mixing and time-consuming decomposition. Therefore, a new non-stationary signal process method that was intrinsic time-scale decomposition (ITD) was put forward by Frei etc. [13], which was successfully used to the processing of biomedical signal. This method can adaptively decompose a complicated signal into proper rotation components (PRCs), whose instantaneous frequency has physical meaning. An et al. [14] proposed a method that base on ITD is used to identify the fault types of the wind turbine bearing. Yang et al. [15] proposed a robust regression-variable predictive mode-based class discriminate method and combined the improved intrinsic time-scale decomposition (IITD) method to make the fault features of bearing signals extract and effectively make the fault types and work conditions of roller bearing identify. Nonetheless, the original ITD algorithm is founded on linear transformation of signal to obtain baseline signal, which may produce distortion and lead to burr [16]. Therefore, to effectively overcome this drawback, an improved ITD algorithm is presented in the paper, which is called ensemble intrinsic time-scale decomposition (EITD).

In recent years, higher order spectral analysis has been deeply studied. Its applications are in many fields: radars, biomedicine, plasma physics, seismic data processing, image reconstruction, and so on. The Wigner higher order spectrum (WHOS) is the fundamental representation in time-varying higher order spectral analysis [17], like the Wigner distribution in the case of time-frequency analysis. WHOS include Wigner bi-spectrum (WB) and Wigner third-order spectrum and so on. WB are the extensions of the Wigner-Ville distribution (WVD), which can reflect the changes of frequency-domain characterization of non-stationary signal [18] and has good time-frequency resolution, however, the cross-terms are its fatal disadvantages [19].

At present, signal analysis methods like Fourier transform, EMD, WT and support vector machine have been used alone or combining two of them for the fault diagnosis of the wind turbine. Such as Tang et al. [20] identify the fault feature and type of the actual wind turbine transmission systems by using a Shannon wavelet support vector machine. Wang et al. [21] based ensemble empirical mode decomposition (EEMD) on independent component analysis to identify gearbox drawbacks, and illustrated the rationality of the provided method in reorganization and diagnosis of the gearbox defect. Hu et al. [22] have applied EITD and wavelet packet transform to recognize the fault types of wind turbine gearbox. Here, we combine EITD with WBE to detect the faults of wind turbine gearbox based on same experimental data.

In spite of that, little research has been carried out on the wind turbine fault diagnosis. Based on that, this paper put forward a new method combining EITD with Wigner bi-spectrum entropy (WBE) to recognize the working state and fault type of wind turbine gearbox. The provided method is applied to remove cross-term interferences and effectively analyze non-stationary amplitude-modulated and frequency-modulated signals from complicated environments as wind plant. In the proposed method, EITD is utilized to decompose the vibration signal of gearbox into PRCs. Next, the principal PRCs are selected to assemble WB according to correlation coefficients and the hard threshold. After the time-frequency distribution is obtained, WBE is extracted as a feature, which is used to recognize the working state and fault type of the gearbox of wind turbine.

The remainder of this paper is organized as follows: Section 2 gives the theoretical description of EITD. In Section 3, a fault diagnosis approach in which EITD and WBE are combined is put forward. In Section 4, the proposed approach is applied in the fault diagnosis of the gearbox of wind turbine, which demonstrates that the provided method is effective and feasible. Conclusions are given in Section 5.

2. EITD method

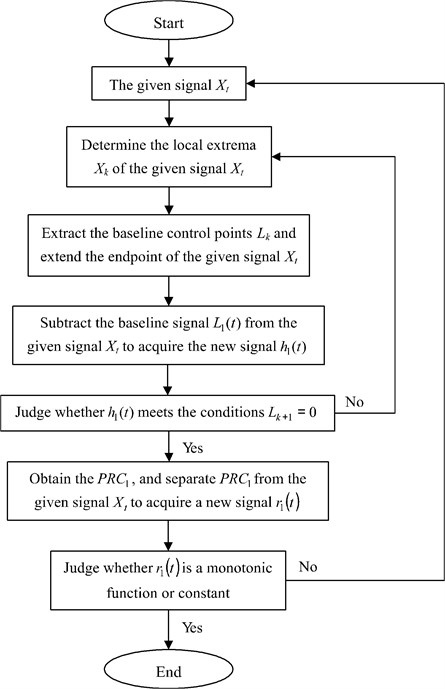
ITD is a self-adaptive time–frequency analysis method. The ITD method decomposes a complicated signal into a sum of PRCs and a monotonic trend, but this method can’t illustrate physical significance of the algorithm itself and the PRC. And the baseline signal is extracted by employing linear transformation to the given signal in original ITD method, which may cause waveform burr and distortion of the decomposed signal. The EMD method uses cubic spline interpolation to fit the upper and lower envelopes, which could give rise to the phenomenon of envelope overshoot or shortage etc. Therefore, combining the linear transformation in original ITD algorithm and the cubic spline interpolation in the EMD method, a novel time-frequency signal analysis method, called EITD, is raised to effectively analyze non-stationary amplitude-modulated and frequency-modulated (AM-FM) signals. Fig. 1 is the flowchart of EITD algorithm. For any given signal $X_t$, the process of EITD can be given as follows:

(1) Determine the local extrema $X_k$ of the given signal $X_t$ and the corresponding moment ${\tau }_k$$\left\{k=\mathrm{1,2},\dots \right\}$, as same as the original ITD method, we define piecewise linear extraction operator $L$ of signals on contiguous extrema interval $[{\tau }_k,{\tau }_{k+1}]$, as follows:

where:

The function value $A_{k+1}$is decided by linking any two-adjacent maximum and minimum $({\tau }_k,X_k)$, $({\tau }_{k+2},X_{k+2})$ at the corresponding time ${\tau }_{k+1}$ between the extremum $X_{k+1}$, are shown below:

(2) Calculate the baseline control points $L_k$ in terms of Eqs (1) and (2), and use the mirror continuation method to dispose of the endpoint of signal $X_t$, and obtain the point of extreme value $({\tau }_0,X_0)$ and $({\tau }_{M+1},X_{M+1})$ on the ends. $k$ is respectively set to be zero and $M-1$, and the values of $L_1$ and $L_M$ are obtained as Eq. (1). Subsequently, the cubic spline interpolation is used to fit the baseline points $L_k$ for obtaining baseline signal $L_1\left(t\right)$.

(3) Subtract the baseline signal $L_1\left(t\right)$ from the given signal $X_t$ to acquire the resulting signal $h_1\left(t\right)$:

Ideally, $h_1\left(t\right)$ is equal to $PR{C}_1$ and is a high-frequency proper rotation component. However, the condition is not really satisfied; so, it is necessary to treat $h_1\left(t\right)$ as the source data and repeat the iterative steps until $h_{1k}\left(t\right)$ is a proper rotation component, that is, the baseline signal needs to meet $L_{k+1}=\text{0}$.

(4) Separate $PR{C}_1$ from the given signal $X_t$ to acquire a new signal $r_1\left(t\right)$:

(5) Repeat the above steps taking $r_1\left(t\right)$ as the original signal to achieve the second proper rotation component ($PR{C}_2$) of the given signal $X_t$, and perform the above process $n$ times, until $r_n\left(t\right)$ turns into a monotonic function to obtain the $n$th proper rotation component ($PR{C}_n$) which satisfy the requirements of $PRC$. Therefore, the signal $X_t$ is decomposed into the sum of $n$$PRC$ and a residual term $r_n\left(t\right)$:

where $p$ is the number of $PRC$. Afterwards, the instantaneous frequency, phase and amplitude can be further obtained. An important problem in EITD method means how to select the terminating criterion which is concerned to the number of iterations and decomposition effects. In this paper, three threshold criterions are adopted to control the iteration times. Define three thresholds ${\theta }_1$, ${\theta }_2$ and ${\mathrm{\Delta }}_k$, and define $a_k=\left|(A_k-X_k)/2\right|$, $L_k=(A_k+X_k)/2$ and ${\mathrm{\Delta }}_k=\left|L_k/{\alpha }_k\right|$, where $k$ is the number of the extreme. The sifting process does not end until ${\mathrm{\Delta }}_k<{\theta }_1$ for fraction $1-\gamma$ of the total time and ${\mathrm{\Delta }}_k<{\theta }_2$ for the remaining part. Generally, $\gamma =\text{0.05}$, ${\theta }_1=\text{0.05}$ and ${\theta }_2=10{\theta }_1$.

Fig. 1The flowchart of EITD algorithm

In order to demonstrate the proposed EITD method, a numerical signal $x\left(t\right)$ denoted as follows is considered:

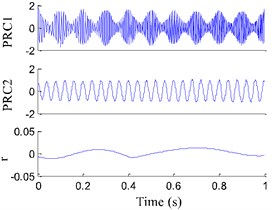
where $R\left(t\right)$ is the random function which denotes the random value of –1 to 1. The sampling frequency of the signal is 1000 Hz and the sampling number is 1000. Fig. 2(a) shows the numerical signal $x\left(t\right)$ and its two components $x_1\left(t\right)$ and $x_2\left(t\right)$, but the component of white noise with amplitude 0.05 is not showed. The signal $x\left(t\right)$ is composed of a AM-FM signal $x_1\left(t\right)$ and a cosine signal $x_2\left(t\right)$, and it is decomposed using EMD, ITD and EITD (See Fig. 2), the four evaluation parameters are given in Table 1.

Fig. 2The signal and its decomposition

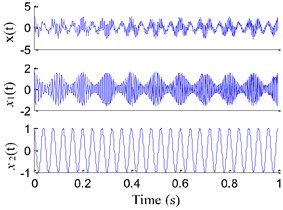
a) Numerical signal $x\left(t\right)$

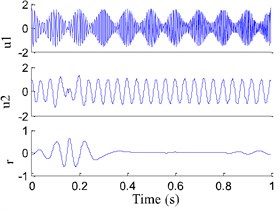
b) EMD

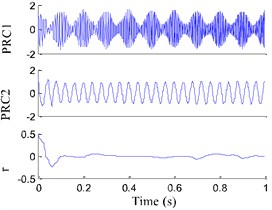
c) ITD

d) EITD

From Fig. 2(d) we could find that the results generated by EITD can accurately reflect the two components of the original signal, and they represent the low frequency (25 Hz) and high frequency (90 Hz). Nevertheless, the second component see Fig. 2(c) in the original ITD method has the clear phenomenon of end effect and waveform burr. From Fig. 2(b) we can see that the second components in EMD exist obvious the phenomenon of mode mixing and curve distortion. Besides, from Table 1 it can be found that the time-consuming of the all components obtained by EMD are more than that obtained by EITD. And the correlation coefficients ${\rho }_1$ and ${\rho }_2$ of the first two PRCs in EITD are higher than those in EMD and ITD. The iteration times $n$ of the EITD is less than those in EMD, which means the EITD decomposition consequences are closer to the real values. The results indicate that EITD is appropriate for the processing of amplitude-modulated and frequency-modulated (AM-FM) signal with multi-component.

3. Fault feature extraction method based on EITD and WBE

WB, as the extended forms of WVD, has played important influence on non-stationary vibration signal analysis, which has a superior distribution and keeps a higher time-frequency resolution. Unfortunately, as for multi-component signals, WB suffer from the unavoidable cross-term interferences, thus are not suitable for many practical applications. For the purpose of solving this problem, combining WB with EITD, a new time frequency analysis method named Wigner bi-spectrum based on ensemble intrinsic time-scale decomposition (EITD-WB) is presented, which can get a superior distribution, hold a higher time-frequency resolution and inhibit the cross-term interferences in WB. Besides, Shannon entropy can be used to reflect the complexity and the uncertainty of the vibration signals, so a new fault feature extraction method founded on EITD and Wigner bi-spectrum entropy (WBE) is further proposed to identify the fault information in wind turbine gearbox. Fig. 3 is flowchart of this method and the process of the proposed fault feature extraction method can be described as follows:

(1) Collect three kinds of state vibration signals $x\left(t\right)$: normal, the gear pitting fault and the gear faults with the broken teeth and worn at sample frequency $f_s$ under a certain speed, and gather $N$ group of samples for each work state.

(2) Apply EITD to decompose the collected vibration signal $x\left(t\right)$ into several PRCs and a residue.

(3) Calculate the correlation coefficients between $PR{C}_i$ ($i=$1, 2,…, $n$) and the collected vibration signal $x\left(t\right)$, as shown below:

where ${\mu }_i$ and ${\mu }_x$ respectively represent the mean value of $PR{C}_i$ and $x\left(t\right)\text{,}$ and ${\sigma }_i$ and ${\sigma }_x$ respectively represent the variance of $PR{C}_i$ and $x\left(t\right)$.

(4) Employ a hard threshold $\lambda$ to select the principal PRCs, and the hard threshold $\lambda$ can be a proportion of the supreme $\rho \left(PR{C}_i,x\right)$, which can be expressed as:

where $\epsilon$ is a scaling factor, $\epsilon =$10.0. Supposing the correlation coefficients $\rho \left(PR{C}_i,x\right)$ is greater than the values of $\lambda$, $PR{C}_i$ is a real component, which is regarded as the principal PRCs.

(5) Calculate the WB of the principal PRCs and it can be listed as follows:

(6) Assemble the WB of all the principal PRCs to obtain the corresponding complete time-frequency distribution, which can be defined by:

where $r$ is the number of the components, and $W\left(t,f_1,f_2\right)$ is the Wigner bi-spectrum based on ensemble intrinsic time-scale decomposition (EITD-WB).

(7) Allocate equally $W\left(t,f_1,f_2\right)$ in the time-frequency plane to achieve the first $N$ time-frequency sections with the same size, and energy of every time-frequency sections is $W_i$ ($i=$1, 2,…, $N$). The normalization processing for $W_i$ can obtain $p_i=W_i/W$. So, Wigner bi-spectrum entropy (WBE) can be defined as:

(8) Calculate the WBE of different vibration signals, and observe the variation trend of WBE to identify the working state and fault type of wind turbine gearbox.

EITD-WB can get a superior distribution, hold a higher time-frequency resolution and inhibit the cross-term interferences. Here we give an example to verify its advantages. The signal $x\left(t\right)$ See Eq. (7) is made up of a AM-FM signal and a cosine signal. Different methods are used to extract the feature of the signal as Fig. 4. It can be shown in Fig. 4(a) that the instantaneous frequencies of the signal are precisely extracted by the WB, but there is a cross-term of 55 Hz both in frequency and time domain in Fig. 4(a). The time-frequency representations (TFR) generated by the WT, shown in Fig. 4(b), can merely indicate the inherent time-frequency pattern of the signal $x\left(t\right)$. The time-frequency representation at 90 Hz demonstrates the clear instantaneous frequency trajectory. However, the representation at 25 Hz is too blur to reveal the IF trajectory. In Fig. 4(c), the cross-term has been eliminated by using WB after Choi-Williams kernel filter, but frequency component of 90 Hz has been deformed, that is to say, the TFR at 90 Hz cannot display the explicit instantaneous frequency trajectory. The result from EITD-WB is shown in Fig. 4(d). It can clearly show that 25 Hz and 90 Hz components are effectively demodulated, and accurately conform to the two AM-FM components in the numerical signal. Obviously, it has also no the cross-term. Therefore, numerical analysis results show that, compared to conventional methods, EITD-WB has perfect time-frequency concentration. In the last step, entropy is used to distinguish the features of signal which mean the type of fault. Thus, the proposed method base on EITD and WBE can effectively extract the feature and identify the working state and fault type.

Fig. 3Flowchart of the proposed fault feature extraction method

Fig. 4The time-frequency representations

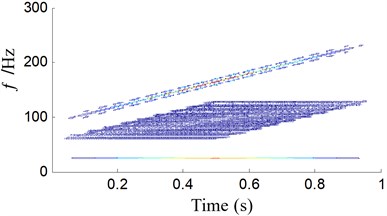
a) Wigner bi-spectrum

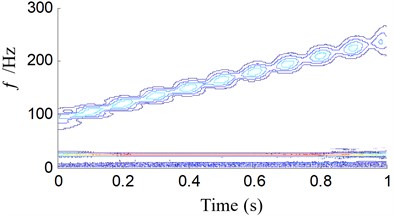
b) Wavelet transform

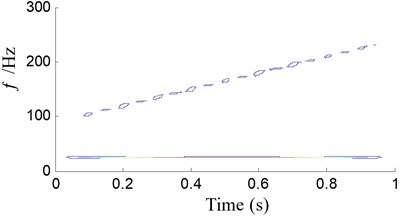
c) Wigner bi-spectrum after Choi-Williams kernel filter

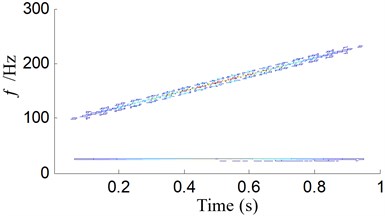
d) EITD-WB

4. Application for fault diagnosis of gearboxes of wind turbine

Gearbox fault of wind turbine is one of the most general faults, which is quite dangerous to the operation of wind turbine. Therefore, the provided method is used to detect gearbox faults to escape unscheduled downtime and catastrophic accidents. The gearbox type for wind turbine is FL1500A. To obtain the data of the gearbox faults, supervisory control and data acquisition (SCADA) system is applied. The sampling frequency was set to be 32768 Hz, and the sampling number was 16384.

Fig. 5 shows pitted gear, and Fig. 6 shows the worn and broken teeth of gear. The gear pitting vibration signal is taken to illustrate the performance of the proposed EITD-WB method. For comparison, EITD and EMD are used to decompose the vibration signal in Fig. 7(b) into five components shown in Fig. 8, respectively.

Fig. 5The pitting faults in secondary level meshing gear

Fig. 6The worn and broken teeth faults in third level gear

Fig. 7The signal waveform in three work states

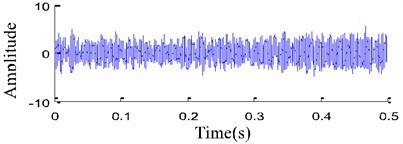
a) Normal

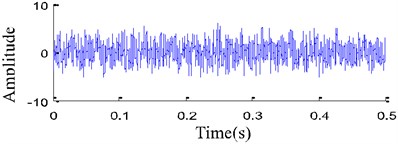
b) Pitted gear fault

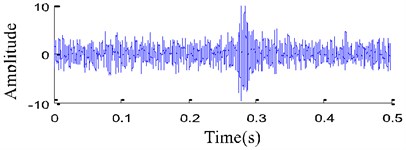
c) Worn and broken teeth faults

Fig. 8Decomposition results

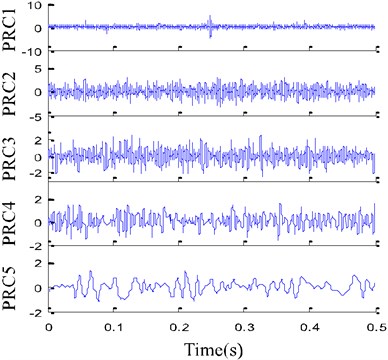
a) EITD

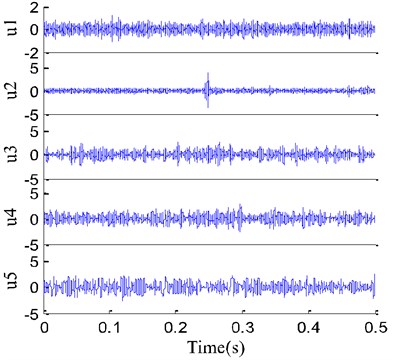
b) EMD for pitting fault signal

The correlation coefficient of each components obtained by EITD and EMD is calculated and the results are shown in Table 2. From Table 2 it is known that the PRC2, PRC3 and PRC4 are principal components and the PRC1 and PRC5 are noise interferences, while the $u_1$-$u_5$ is regarded as the principal components. Therefore, the PRC2, PRC3 and PRC4 are chosen to assemble WB, while $u_1$-$u_5$ is used to assemble WB. The time-frequency distribution obtained by EITD-WB is shown in Fig. 9(a), which has the WB’s high resolution characteristic but eliminates the cross-term for EITD. Meanwhile, from Fig. 9(a), it is clear that the frequency is mainly concentrated in 6.2 Hz, which is equal to fault characteristic frequency of the gear with pitting. However, as shown in Fig. 9(b), the time-frequency distribution obtained by WB based on EMD (EMD-WB) has obvious cross-term in high frequency. The results show that EITD-WB can not only remove cross-term interference in WB, but also keep all the good qualities of the WB, which lays a foundation for the next fault feature extraction.

Fig. 9The time-frequency representations

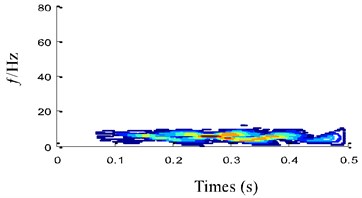
a) EITD-WB

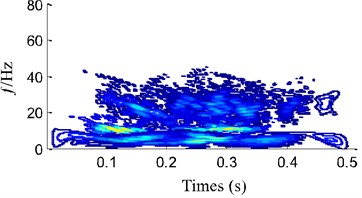
b) EMD-WB

We choose 15 groups data from SCADA of the wind plant, which include three work states: normal, pitted gear fault and worn and broken teeth faults. According to the flowchart in Fig. 3, WBE can be obtained by combining the Shannon entropy and WB to extract the state feature. The result is shown in Fig. 9, which has very good stability and classification effect. Moreover, WBE of gear vibration signal in normal state is the maximum from Fig. 10, which conforms to the uniformity and uncertainty of energy distribution in frequency spectrum of gear vibration signal in the normal state. The WBEs of the other two fault conditions are smaller, because the energies of fault states whether pitting fault or worn and broken teeth faults are mainly focused on resonance frequency bands. The results indicate that WBE based on EITD can characterize the complexity of signal, and availably depict the dynamic change of vibration signal, and has very good anti-jamming ability. Besides, the proposed method can effectively identify the vibration characteristics of wind turbine gear and provides a new idea for accurate diagnosis of working state and faults of wind turbine gear.

In order to evaluate the performance of the proposed fault diagnosis method based on WBE and EITD in this paper, the following comparison is given. The effect of distribution with WBE is compared with the other two entropy algorithms of power spectrum entropy (PSE) and envelope spectrum entropy (EPE). The distributions of entropy value of PSE and EPE are shown in Fig. 11. Fig. 11 indicates that PSE or EPE cannot effectively discriminate between the three different types of patterns. As shown in Fig. 11 that while using PSE, there were overlaps between the values of pitting fault and broken teeth fault, also the normal state is mixed with the pitting fault while EPE. It reveals that WBE has more excellent clustering performance than both PSE and EPE.

This application adequately points the superior performance of the proposed method which combines EITD with WBE. The method can remove cross-term interference, and keep high time-frequency resolution and good energy aggregation. Pattern recognition also provided better performance than other algorithms, and the proposed method is more favorable to distinguish the different faults type.

Fig. 10The distribution of entropy value with Wigner bi-spectrum entropy (WBE): 1 – normal, 2 – pitting, 3 – worn and broken teeth

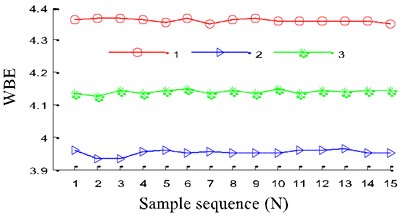
Fig. 11The distribution of entropy value: 1 – normal, 2 – pitting, 3 – worn and broken teeth

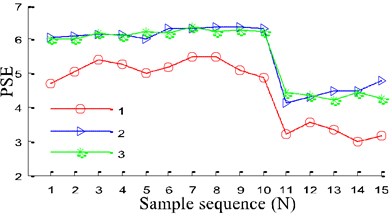
a) Power spectrum entropy

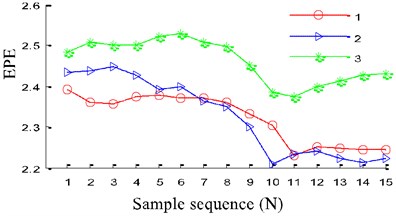
b) Envelope spectrum entropy (ESE)

5. Conclusions

In this paper, a new synergistic idea of EITD and WBE is applied to tackle nonlinear fault diagnosis. The observations and conclusions of the study are summarized as follows:

1) EITD, a novel time-frequency analysis method, is proposed to effectively analyze non-stationary signals. The results show that the new method is better than the EMD and ITD methods.

2) The time-frequency representations are investigated in this paper using different method. EITD-WB has perfect time-frequency concentration and can effectively extract the feature of the signal.

3) The novel strategy of utilizing combined EITD and WBE to fault recognition in wind turbine gearbox is developed, and the algorithm is proved effective to identify the working state and fault type of wind turbine. It was provided an effectual way for the fault identification of wind turbine to combine EITD and WBE.