Vibration signal de-noising based on empirical wavelet transform autocorrelation analysis

2.1. Empirical wavelet transform

The empirical wavelet transform decomposes the signal $f\left(t\right)$ into the sum of the modal functions $f_i\left(t\right)$. The modal functions are considered as follows:

where $f_i\left(t\right)$ is intrinsic modal component for EWT decomposition.

First, the Fourier spectrum of the signal is divided, and the frequency range of the Fourier spectrum of the signal is defined as $[0,\pi ]$. The $N$ maximum in the spectrum is found and the spectrum is divided into N continuous intervals ${\mathrm{\Lambda }}_n$, and the boundary of the two adjacent bands is expressed by ${\omega }_n$, in which the ${\omega }_n$ is the middle point of the two adjacent maximum points of the signal Fourier spectrum, and the partition interval is expressed as:

After determining the segmentation interval, adding wavelet window to each interval. According to the construction method of the Meyer wavelet [12], the empirical scale function is:

The empirical wavelet function is:

where $\gamma$ shall satisfy the following condition: $\gamma <\mathrm{m}\mathrm{i}{\mathrm{n}}_n[{\omega }_{n+1}-\raisebox{1ex}{${\omega }_n$}\!\left/ \!\raisebox{-1ex}{${\omega }_{n+1}$}\right.+{\omega }_n]$; $\beta \left(x\right)$ shall satisfy the following condition: $\beta \left(x\right)=x^4(35-84x+70x^2-20x^3)$.

2.2. Proposed denoising method

First, the noise signal $f\left(t\right)$ is decomposed by EWT, and $i$ intrinsic modal components are obtained. Then, the demarcation point $j$ is determined by the mean square error criterion proposed by Boudraa [13]. Furthermore, the autocorrelation denoising is carried out for noise dominated components, and the components of noise cancellation are $ewt\left\{j+1\right\},ewt\{j+2\},\dots ,ewt\left\{i\right\}$. Finally, the high frequency component after de-noising and the low frequency component are reconstructed.

3.1. Experiment condition

The real vibration signal of this paper is provided by the simulation experiment of the fire failure of WD615 diesel engine. The experimental device is shown in Fig. 1, the A area is PXI data acquisition system of the national instrument company of the United States, which can be used to collect the signal of the vibration sensor by the acquisition system. According to the experimental data analysis of the sampled vibration signals, it is found that the propagation distance of the vibration signal is proportional to the attenuation amplitude of the vibration signal. For the six cylinder diesel engine, the two vibration sensors can collect the vibration signal more accurately than the single sensor, and save the cost of the instrument. Therefore, in the area B and C, a vibration sensor is installed on top of the 6# cylinder head and the other one is installed on top of the 1# cylinder head respectively to collect vibration signals of the diesel engine.

In this experiment, the normal running speed of WD615 diesel engine is about 900 r/min, the experimental sampling frequency is 25600 Hz, the sampling time is 5 s, and the data sample length is 128000 data points.

Fig. 1Experimental device diagram

3.2. Experimental data processing

The vibration signal of normal operation of diesel engine is displayed in a complete working cycle, as shown in Fig. 2. The vibration signal of the working cycle is decomposed by EWT, the number of spectrum segments is decomposed by $N=$ 5, and the decomposition results are shown in Fig. 3.

From Fig. 3, it can be found that the frequency components of diesel engine vibration signal are more complex, multiple modal components contain noise interference, low frequency noise interference is small, and high frequency component noise interference is obvious. The vibration signal is processed by EWT autocorrelation denoising, as shown in Fig. 4. Compared to Fig. 3 and Fig. 4, it is found that the amplitude of each component is greatly reduced after the noise elimination, and the effect of the noise elimination is remarkable in the whole, but there is still no ideal at the end point.

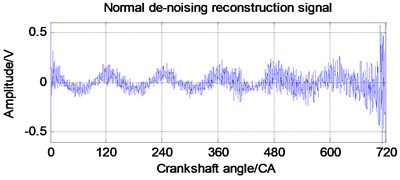
The denoising and reconstruction signal is shown in Fig. 5. The reconstructed signal eliminates the influence of the periodic noise components, and preserves the periodic components of the original signal, and the denoising effect is obvious. The results show that the EWT autocorrelation denoising method is effective.

Fig. 2Vibration signal of normal operation of diesel engine

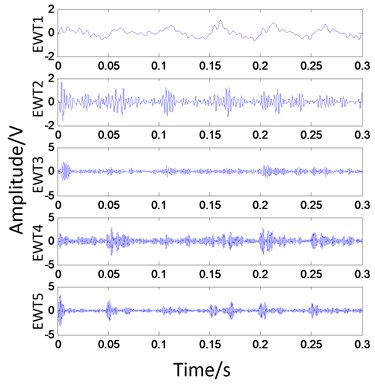
Fig. 3EWT decomposition of vibration signal

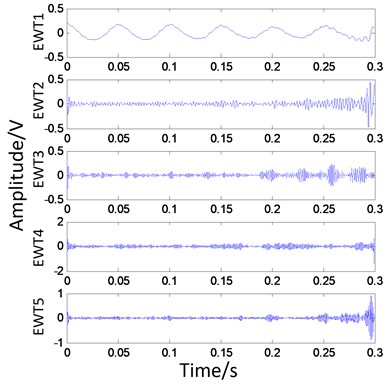
Fig. 4EWT autocorrelation denoising of vibration signal

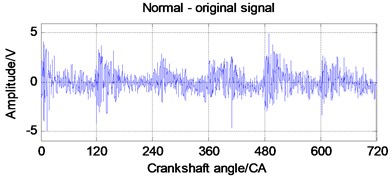
Fig. 5Denoising reconfiguration signal