Vision-based displacement test method for high-rise building shaking table test

2.1. The vision-based displacement method

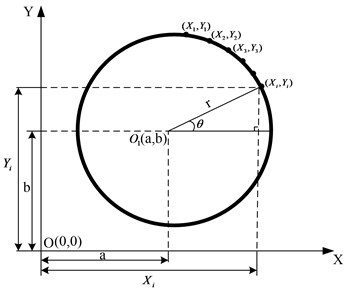
The important issues of the method are the circle detection algorithm and the calibrate relationship. The vision-based displacement test method was based on the basic principle of circle detection using the least squares method (LSM), LSM method uses the target circle’s edge point coordinates just doing one operation, and the target circle parameters (center coordinates and radii) can be obtained. The algorithm flow is shown in Fig. 1, in which, “edge” is the edge of target circle in the image, ($X_i$, $Y_i$) is the edge point coordinates of target circle. The asymptotic time complexity of the algorithm is $O\left(n\right)$, which has high computational efficiency.

Fig. 1Schematic diagram of algorithm flow

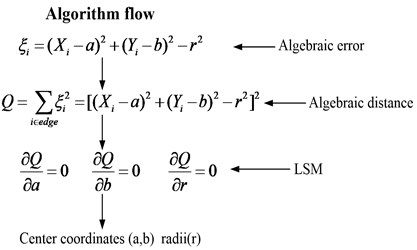
The calibration relationship between image pixel and actual displacement is illustrated in Fig. 2. From the Fig, it is clear that, at initial time, the center of target circle post in ($X_0$, $Y_0$), when at τ moment, the center of target circle moves to position ($X_1$, $Y_1$), relative pixel distance between center position ($X_i$, $Y_i$) and initial position ($X_0$, $Y_0$) can be defined as $\mathrm{\Delta }{X}_i$ and $\mathrm{\Delta }{Y}_i$, $\mathrm{\Delta }{X}_i$ and $\mathrm{\Delta }{X}_i$ both can be accessed in terms of every time step. The radius of target circle in each image can be obtained through the circle fitting algorithm, Eq. (1) marks the average of radius of target circle:

In which, $n$ is the total number of image, $R_i$ is the radius of target circle in each image.

Take the radius of target circle equals 1 cm in actual space for example, the relationship between 1 cm in actual space and pixel in image space is: $R$ (pixel)$=$1 (cm). Therefore, the horizontal displacement and vertical displacement in actual space are: $D_x=\mathrm{\Delta }{X}_i/R$ and $D_Y=\mathrm{\Delta }{Y}_i/R$, respectively.

The flowchart of vision-based displacement test system is shown in Fig. 3. The video is captured by camera, and read by software. Center coordinates and radii of target circles can be obtained by the circle fitting algorithm. Then, the center coordinates are stored according to the continuous static image sequence; therefore, the horizontal and vertical displacements of the target circle center in the image space were obtained. By calibrating the relationship between the image pixels and coordinates of the actual objects, the actual displacement can be obtained. The self-developed software is based on the C++ and OpenCV.

Fig. 2Schematic diagram of calibration relationship between image pixel and actual displacement

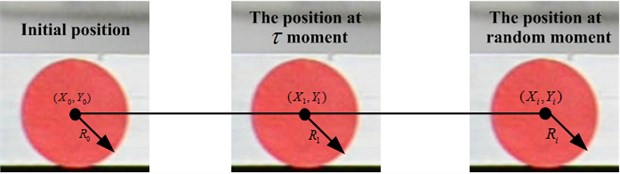
Fig. 3The flowchart of vision-based displacement system

2.2. Verification on vision-based displacement measurement system

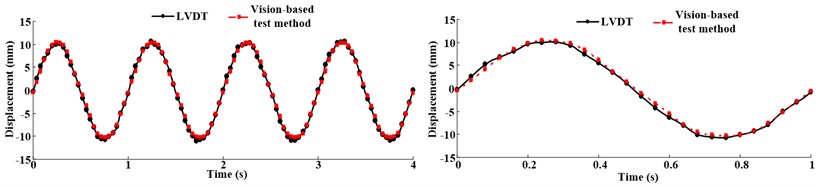
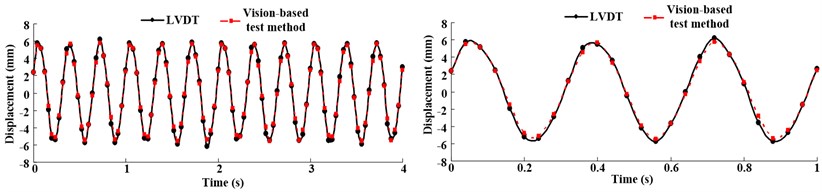
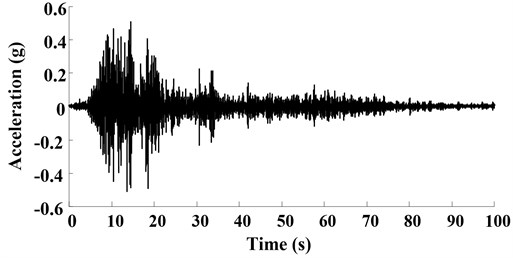
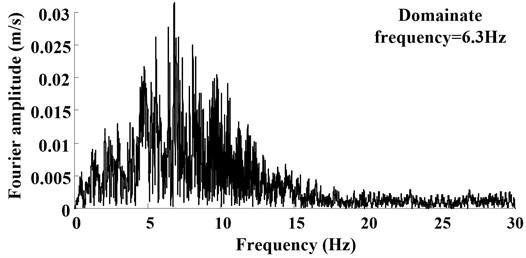
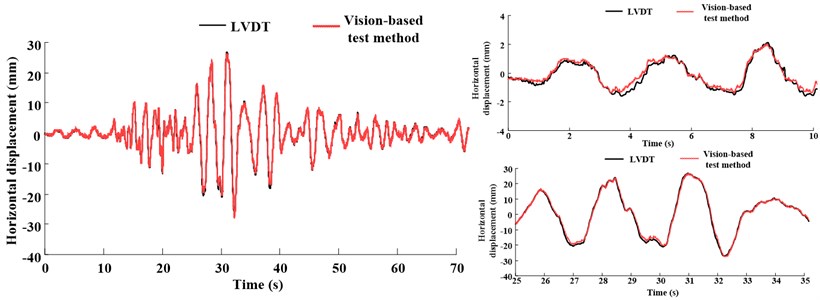
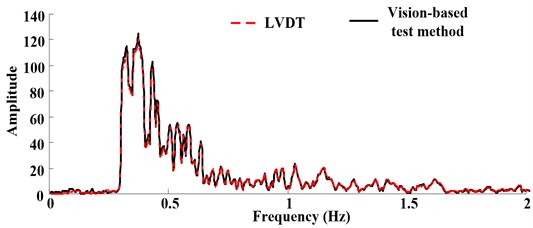
Fig. 4 shows the experimental condition. The displacement obtained by vision-based test method will be identical to the displacement measured by laser displacement meter (LVDT). Fig. 5 shows the displacement response under 1 Hz, 3 Hz input motion, it is clear that, the measurement of vision-based displacement test method is identical to that measured by LVDT. However, in practical engineering, the displacement may be causes by various vibration, such as earthquake, aeolian vibration, vortex-induced vibration which would contain various frequency components. In this research, Songpan ground motion (Ms8.0 Wenchuan Earthquake, China) was adopted as input motion to verify the proposed method. Acceleration time history curves and Fourier spectra are shown in Fig. 6, the dominant frequency of input motion is 6.3 Hz. Fig. 7 shows the displacement of the rigid specimen measured by vision-based displacement method and LVDT, it is clear that, the displacement measured from the LVDT and the displacement measured by proposed method was discovered to be similar, the proposed method can measure the dynamic displacement relatively well both in time-domain and frequency-domain.

Fig. 4The typical picture of experimental condition

a)

b)

Fig. 5Displacement response comparing the vision-based test method and actuator LVDT feedback under 1 Hz and 3 Hz

a)

b)

Fig. 6Ground motion acceleration time histories and Fourier spectra on the shaking table surface

a)

b)

Fig. 7Displacement response comparing the vision-based test method and actuator LVDT feedback under earthquake ground motion

a)

b)

To analyze the measured displacement results, the accuracy and precision of measurement results from this study are compared using percent error of Eq. (2), RMSE (root-mean-square error) of Eq. (3), in which, $n$ is the total number of images, $V_i$ is the displacement measured by vision-based displacement test method, $M_i$ is the displacement measured by LVDT. Table 1 lists the obtained accuracy statistics of the development vision-based displacement test method and LVDT, it is clear that, under different input conditions, the proposed method always has an equal level of measurement degree to the LVDT feedback since the percent error was 1.75 % for 1Hz sine wave, 0.65 % for 3 Hz sine wave, 0.9 % for Songpan ground motion, respectively. The RMS error was 0.97 mm for 1 Hz sine wave, 0.31 mm for 3 Hz sine wave, 0.52 mm for Songpan earthquake, respectively. Thus, it is judged that the suggested displacement measurement method is able to evaluate the dynamic displacement:

3.1. Test apparatus, test case and layout of sensors

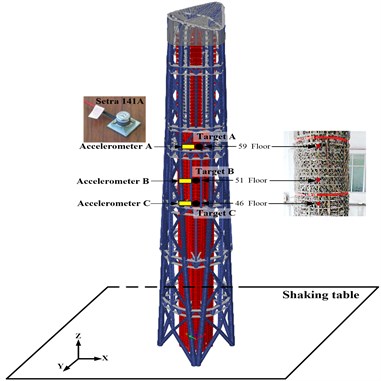
The dimension of shaking table was 6.0 m×6.0 m in plane in China Academy of Building Research (CABR). The maximum acceleration of shaking table was 1.5 g with the maximum proof mass of 80 tons, where g is the gravitational acceleration. The frequency of the input motion ranges from 0.1 to 50 Hz. The detailed technology parameters of the shaking table is listed in Table 2. The height of tested building is 11.008 m with 95 floors, the similarity ratios of model structure are shown in Table 3. 64 acceleration sensors (model: Setra 141A) were installed in different position of the building, the high-rise building and layout of sensors are shown in Fig. 8. In 46, 51, 59 floors, the targets were installed to compare the displacement data calculated by accelerometers, and correct the integration parameters. The test cases are shown in Table 4. The camcorder used in this test is Panasonic HDC-TM700, which has 1920×1080 pixels of resolution and is able to measure almost 60 frames per second, the optical equipment (such as lenses, and cameras, etc.) and target size play important roles in vision-based measurement system.

Table 4Test cases for the shaking table tests (Normalization in acceleration)

Test case	Acceleration records in $X$ direction (m/s-2)	Acceleration records in $Z$ direction (m/s-2)
S835		None
S836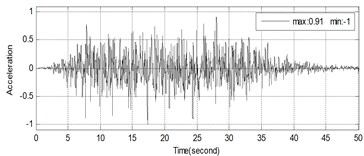
L840		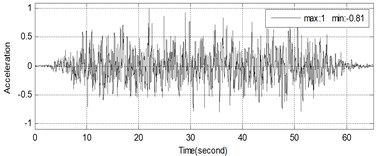None

Fig. 8The high-rise building and layout of sensors

3.2. Results and analysis

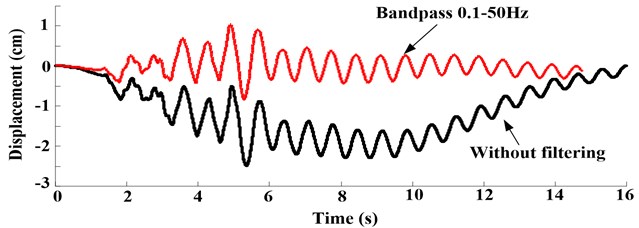
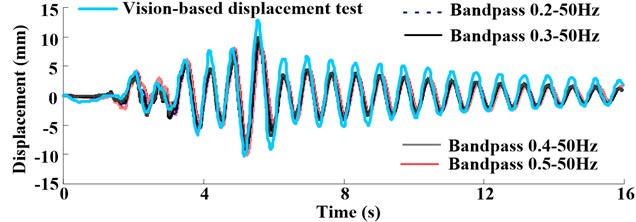
Figs. 9-10 depict the comparisons between the displacement measured by vision-based displacement test method and that obtained by integration form acceleration which installed in the 59 floor.

Fig. 9Displacement response comparing the vision-based test method and integration in test case S835 that the PGA is 0.2 g

a)

b)

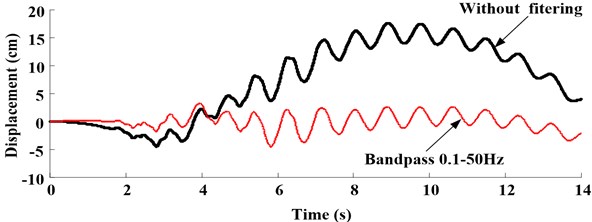
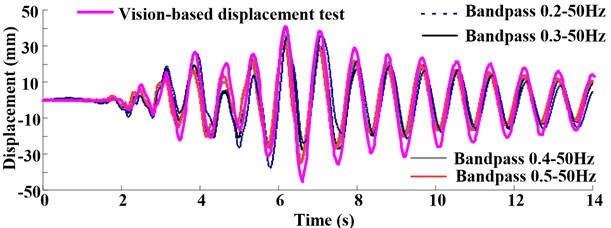
Fig. 10Displacement response comparing the vision-based test method and integration in test case L840 that the PGA is 0.4 g

a)

b)

The results show that if integration without filtering, the displacement will drift. With the increase of low-frequency, the shapes of displacement show more reasonable comparison with real displacement, however, the peak of displacement measured by integration was less than that measured by vision-based displacement test method. This may be caused by noise existing in the experiment and the integral terms generated from integration process, which need to be proposed by baseline concretion and filtering. Generally, choose 1/3 first order natural frequency of structural system to filter the signal (in this test, the first order natural frequency of structural system before shaking is 1.53 Hz). The process will damp certain signals, which make signal energy falling.

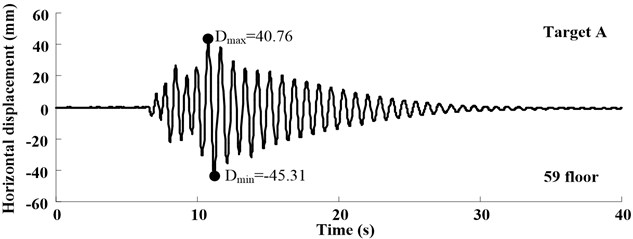
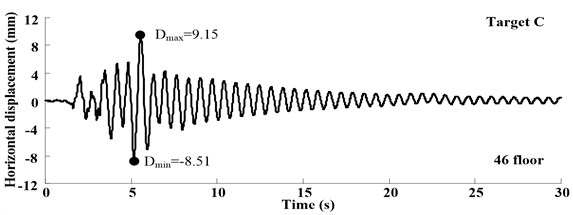
The time histories of displacement measured in Target A-C at different loading conditions are shown in Figs. 11-13, which illustrate the free-vibration characteristics of damping system. Moreover, at the test case in S836, when input multi-dimensional shaking, the one-way acceleration sensor can’t test bidirectional displacement, vision-based displacement can obtain both horizontal and vertical displacement.

Fig. 11Displacement response at different test position in test case L840 that the PGA is 0.4 g

a)

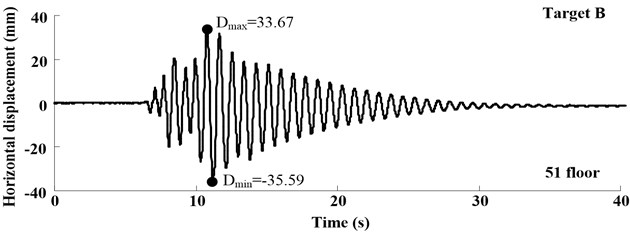
b)

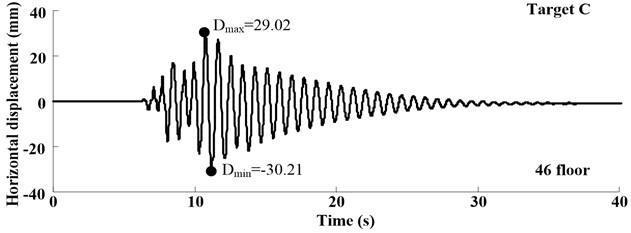
c)

3.3. Discussion of the vision-based test method

The vision-based displacement method can only track the motions in flat surfaces (as $X$, $Z$ axes in the shaking table test). The method cannot be performed on all axes ($X$, $Y$ and $Z$ axes), the binocular vision can solve this problem. Moreover, the measurement values are unstable depending on the movement of the camera support and are affected by the accuracy of their adherence to the target. Despite the disadvantages, the vision-based measurement can be applied to the locations where displacement transducer is difficult to attach and it can be in a bidirectional motion.

Fig. 12Displacement response at different test position in test case S835 that the PGA is 0.2 g

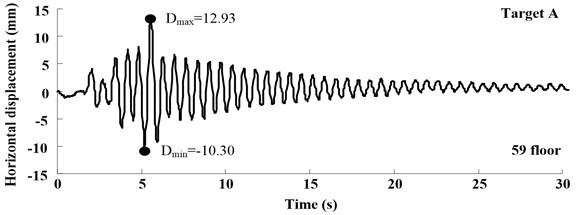
a)

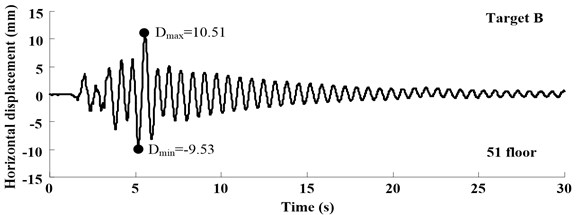
b)

c)

Fig. 13Displacement response at different test position in test case S836 that the PGA is 0.2 g

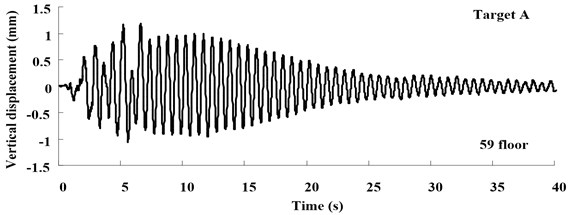
a)

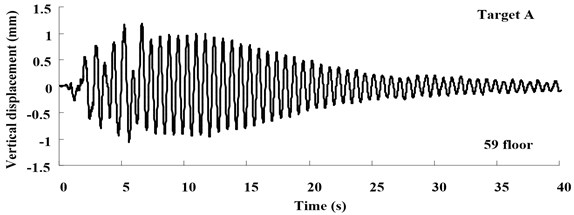
b)