Damping multi-model adaptive switching controller design for electronic air suspension system

Sun, Xiaoqiang; Cai, Yingfeng; Wang, Shaohua; Chen, Long

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2015

Check for updates

Damping multi-model adaptive switching controller design for electronic air suspension system

Xiaoqiang Sun¹

Yingfeng Cai²

Shaohua Wang³

Long Chen⁴

^{1, 2, 3, 4}School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang, China

Corresponding Author:

Long Chen

Cite the article Download PDF

Downloads 1525

Abstract

This paper presents the design and verification of a damping multi-model adaptive switching controller for electronic air suspension (EAS) system. In order to improve the convergence rate of identification algorithm of conventional adaptive controller, multiple local linear full-car vehicle models of EAS system with fixed parameters are established according to the actual damping control process of EAS for different vehicle driving conditions and an adaptive model whose initial value of parameters can be re-assigned is introduced to enhance the system control precision. The model switching control strategy based on minimum error is used to select the best matching model online and the optimum damping force is regulated by adaptive control algorithm, thus constituting the damping multi-model adaptive control for EAS. Simulation results show that the control method proposed in this paper can improve the damping regulating performance of EAS effectively in wide range driving conditions, especially for the case of sudden change in driving conditions.

1. Introduction

As an important component of vehicle chassis, suspension plays a pivotal role to guarantee the ride comfort, handling stability and driving safety for the moving vehicle [1]. In the past few decades, active or semi-active suspension, which utilize advanced electronic control technology, have received extensive attentions in automotive industry [2-4]. Active suspension can improve suspension performance by controlling the force generated by means of an actuator, but high cost, large energy consumption and control time delay become important factors to restrict its development [5, 6]. Relatively speaking, semi-active suspensions are wide-spread in industrial application because of their performance increase compared to passive suspensions and their lower energy consumption and control cost compared to active systems [7]. Many methods for controlling semi-active suspension systems have been proposed, while although they have been confirmed that have the ability to offer performance benefits for semi-active suspensions, the great majority researches are conducted based on the spring stiffness is not variable.

EAS system uses electronic technology to control vehicle height and semi-active damping force, thus achieving automatic modulation of suspension characteristics appropriate to riding, handling and road conditions [8-10]. An important difference between the air suspension and the traditional passive suspension is that the stiffness of air spring is variable, which brings new challenges for the controlling of damping force for EAS system [11]. Adaptive control is one of the advanced control methods that are aimed at a class of controlled objects which have varying degrees of model uncertainty [12, 13]. It can provide high quality control performance and achieve optimal regulation of system states on condition that the model parameters are incomplete or poorly understood. However, due to the obvious time varying and sudden change phenomena of model parameters of EAS system, the identification algorithm convergence rate of conventional adaptive controller can’t follow the actual change speed of model parameters, which gives rise to the inaccurate of identification model and then lead to poor performance of the adaptive controller based on this model.

In this paper, we describe how the multi-model adaptive switching control framework can be successfully applied for solving the damping control problem of EAS in a systematic way. Nine linear full-car models with fixed parameters and an adaptive model of EAS system are established and a model switching control strategy is designed. The simulation response of the multi-model adaptive switching controller is compared with that of the conventional adaptive controller to evaluate corresponding performances finally.

2. Damping control process analysis of EAS

2.1. Variable stiffness characteristics of air spring

The air spring considered in this study is a diaphragm air spring with its piston cylindrical. It contains head, piston and sleeve as shown in Fig. 1. The base of the rubber sleeve is fastened to the top of the piston and rolls along the lateral surface of the cylindrical piston.

Fig. 1Diaphragm air spring

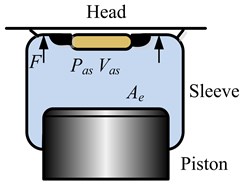
Equation of the vertical elastic force of air spring is given by the following:

1

F = (p_{a s} - p_{a}) A_{e} = p_{e} A_{e},

where $F$ is the vertical elastic force of air spring, $p_{a s}$ is the absolute pressure inside air spring, $p_{a}$ is the atmospheric pressure, $A_{e}$ is the cross-sectional area of air spring, $p_{e}$ is the relative pressure inside air spring. According to the definition of spring stiffness, the stiffness of air spring can be obtained as follows [14]:

2

k = \frac{d F}{d s} = \frac{d (p_{e} A_{e})}{d s} = p_{e} \frac{d A_{e}}{d s} + A_{e} \frac{d p_{e}}{d s},

where $k$ is the stiffness of air spring, $s$ is the vertical displacement of air spring.

The gas process that defines the relationship between pressure and specific volume in air spring is given by the polytropic relationship:

3

p_{a s} V_{a s}^{n} = c o n s t,

where $V_{a s}$ is the specific volume of air spring, $n$ is the polytropic index. Differentiation of Eq. (3) of $s$ gives:

4

V_{a s}^{n} \frac{d p_{a s}}{d s} + n V_{a s}^{n - 1} p_{a s} \frac{d V_{a s}}{d s} = 0 .

Therefore the differentiation of $p_{e}$ of $s$ can be obtained as:

5

\frac{d p_{e}}{d s} = \frac{d p_{a s}}{d s} = - \frac{n p_{a s}}{V_{a s}} \frac{d V_{a s}}{d s} = \frac{n p_{a s}}{V_{a s}} A_{e} .

For the diaphragm air spring with its piston cylindrical, the cross-sectional area is assumed to be constant in normal working stroke, so the air spring stiffness can be further obtained as:

6

k = p_{e} \frac{d A_{e}}{d s} + n p_{a s} \frac{{A_{e}}^{2}}{V_{a s}} = n p_{a s} \frac{{A_{e}}^{2}}{V_{a s}} = n \frac{F_{a s}}{H_{a s}},

where $H_{a s}$ is the vehicle height. From Eq. (6), it can be seen obviously that the absolute pressure inside air spring and the air spring specific volume have direct influence on the air spring stiffness. Among of them, the $p_{a s}$ mainly depends on the vertical load of air spring, while the $V_{a s}$ is impacted by the length of air spring.

2.2. The influence of vehicle height adjustment on air spring stiffness

Vehicle height adjustment is one of the main features of EAS and it consists of two parts: the general adjustment and the stable adjustment. Fig. 2 shows the vehicle height adjustment strategy. The general adjustment is aimed at regulating the vehicle height for different driving conditions, for example, when the car is driving on off-road way, the vehicle height adjustment system can lift the vehicle height from “Normal mode” to “Off-road mode”, thus improve the ride comfort and reduce the probability of suspension reaches the mechanical end stop, while for high-speed driving condition, lowering the vehicle body from “Normal mode” to “Highway mode” can not only reduce the air drag, but also improve the driving stability [15]. Meanwhile, after choosing the suitable vehicle height mode, the stable adjustment will be used to maintain the vehicle height to prevent deviation between the actual vehicle height and the target vehicle height, e.g. when the vehicle load is largely changed.

Fig. 2Vehicle height adjustment strategy

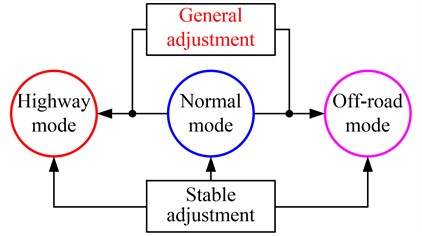
According to the vehicle height adjustment principle, the influence mechanism on air spring stiffness of the two vehicle adjustment functions is different. The general adjustment can be regarded as influencing the air spring stiffness by regulating the air spring length on the premise that the absolute pressure inside air spring is unchanged. However, for the stable adjustment, it can impact the air spring stiffness through changing the absolute pressure inside air spring while the air spring length remains unchanged.

3. Dynamic modeling of EAS system

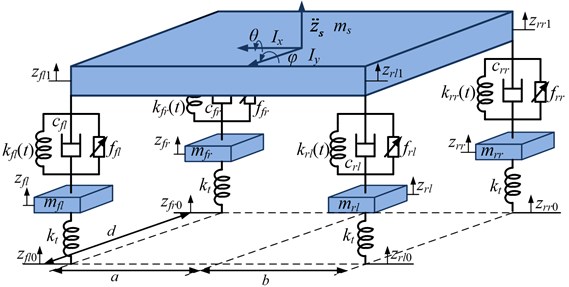
The EAS system model established for damping control is a full-car model. The system consists of the vehicle body, four air suspensions, four unsprung masses and four tires as shown in Fig. 3. Assumptions of the modeling are as follows: the air spring is modeled as a linear spring with its stiffness time-varying; the adjustable damping shock absorber is equivalent to a nominal passive damping and a controllable damping force; the tire, which is always in contact with the road surface, is simplified as a linear spring with its damping effect neglected.

Equations of motion for full-car model are given by the following [16]:

7

\{\begin{array}{l} m_{s} {\ddot{z}}_{s} = F_{f l} + F_{f r} + F_{r l} + F_{r r}, \\ I_{x} \ddot{θ} = (F_{f r} + F_{r r} - F_{f l} - F_{r l}) d, \\ I_{y} \ddot{φ} = b (F_{r l} + F_{r r}) - a (F_{f l} + F_{f r}), \\ m_{f l} {\ddot{z}}_{f l} = k_{t} (z_{f l 0} - z_{f l}) - F_{f l}, \\ m_{f r} {\ddot{z}}_{f r} = k_{t} (z_{f r 0} - z_{f r}) - F_{f r}, \\ m_{r l} {\ddot{z}}_{r l} = k_{t} (z_{r l 0} - z_{r l}) - F_{r l}, \\ m_{r r} {\ddot{z}}_{r r} = k_{t} (z_{r r 0} - z_{r r}) - F_{r r}, \end{array}

\{\begin{array}{l} F_{f l} = k_{f l} (t) (z_{f l} - z_{f l 1}) + c_{f l} ({\dot{z}}_{f l} - {\dot{z}}_{f l 1}) + f_{f l}, \\ F_{f r} = k_{f r} (t) (z_{f r} - z_{f r 1}) + c_{f r} ({\dot{z}}_{f r} - {\dot{z}}_{f r 1}) + f_{f r}, \\ F_{r l} = k_{r l} (t) (z_{r l} - z_{r l 1}) + c_{r l} ({\dot{z}}_{r l} - {\dot{z}}_{r l 1}) + f_{r l}, \\ F_{r r} = k_{r r} (t) (z_{r r} - z_{r r 1}) + c_{r r} ({\dot{z}}_{r r} - {\dot{z}}_{r r 1}) + f_{r r}, \\ z_{f l 1} = z_{s} - a φ - d_{1} θ, \\ z_{f r 1} = z_{s} - a φ + d_{1} θ, \\ z_{r l 1} = z_{s} + b φ - d_{1} θ, \\ z_{r r 1} = z_{s} + b φ + d_{1} θ, \end{array}

where $m_{s}$ is the vehicle body mass, $m_{f l}$ , $m_{f r}$ , $m_{r l}$ and $m_{r r}$ are the unsprung masses at four corners of the vehicle, $I_{x}$ and $I_{y}$ are the roll inertia and pitch inertia of the vehicle body respectively, $z_{s}$ is the displacement of the vehicle body, $θ$ and $φ$ are the roll angle and pitch angle of the vehicle body respectively, $z_{f l}$ , $z_{f r}$ , $z_{r l}$ and $z_{r r}$ are the displacement of the unsprung masses, $F_{f l}$ , $F_{f r}$ , $F_{r l}$ and $F_{r r}$ are the four air suspension forces, $d_{1}$ is half of the distance between the left wheel and the right wheel $d$ , $a$ and $b$ are the distance of front shaft and rear shaft to vehicle center of gravity (C.G.), $k_{t}$ is the stiffness of tire, $z_{f l 0}$ , $z_{f r 0}$ , $z_{r l 0}$ and $z_{r r 0}$ are the road displacement inputs at four tires, $k_{f l} (t)$ , $k_{f r} (t)$ , $k_{r l} (t)$ and $k_{r r} (t)$ are the equivalent time-varying stiffness of four air springs, $z_{f l 1}$ , $z_{f r 1}$ , $z_{r l 1}$ and $z_{r r 1}$ are the displacement of the four corners of vehicle body, $c_{f l}$ , $c_{f r}$ , $c_{r l}$ and $c_{r r}$ are the damping of the four nominal dampers, $f_{f l}$ , $f_{r}$ , $f_{r l}$ and $f_{r r}$ are the four controllable damping forces, $d_{1}$ is a half of $d$ .

Fig. 3Full-car model of EAS

After choosing the state variables and the output variables as:

8

\{\begin{array}{l} x = {[\begin{array}{l} z_{f l} & z_{f r} & z_{r l} & z_{r r} & z_{s} & θ & φ & {\dot{z}}_{f l} & {\dot{z}}_{f r} & {\dot{z}}_{r l} & {\dot{z}}_{r r} & {\dot{z}}_{s} & \dot{θ} & \dot{φ} \end{array}]}^{T}, \\ y = {[\begin{array}{l} {\ddot{z}}_{s} & \ddot{θ} & \ddot{φ} & z_{f l 1} - z_{f l} & z_{r l 1} - z_{r l} & k_{t} (z_{f l 0} - z_{f l}) & k_{t} (z_{r l 0} - z_{r l}) \end{array}]}^{T} . \end{array}

Eq. (7) can be written in the following state-space form as:

9

\{\begin{array}{l} \dot{x} = A x + B u + F w, \\ y = C x + D u + G w, \end{array}

where $u$ represents the external controllable damping force of the EAS system, $w$ represents the disturbance caused by road roughness. $A$ , $B$ , $C$ , $D$ , $F$ and $G$ are the relevant constant matrices, which are omitted here for lack of space.

By taking Laplace transformation for Eq. (9), we obtain:

10

\{\begin{array}{l} s X (s) = A X (s) + B U (s) + F W (s), \\ Y (s) = C X (s) + D U (s) + G W (s) . \end{array}

Then, the mapping relationship between the system output and the system input is given as:

11

Y (s) = [C (s I - A)^{- 1} B + D] U (s) + [C (s I - A)^{- 1} F + G] W (s) .

Substituting the constant matrices into Eq. (11) and conducting discretization by using Euler method, we can get the system discrete time model with time-varying parameters as:

12

A_{1} (t, q^{- 1}) y (t) = B_{1} (t, q^{- 1}) u (t - 1) + C_{1} (t, q^{- 1}) w (t - 1),

where:

13

\{\begin{array}{l} A_{1 i} (t, q^{- 1}) = 1 + a_{1 i} (t) q^{- 1} + \cdot \cdot \cdot + a_{m i} (t) q^{- m}, \\ B_{1 i} (t, q^{- 1}) = b_{0 i} (t) + b_{1 i} (t) q^{- 1} + \cdot \cdot \cdot + b_{n i} (t) q^{- n}, \\ C_{1 i} (t, q^{- 1}) = c_{0 i} (t) + c_{1 i} (t) q^{- 1} + \cdot \cdot \cdot + c_{p i} (t) q^{- p}, i = 1, \dots, 7, \end{array}

$m$ , $n$ and $p$ are the model order, which are set according to the simulation precision requirement, $q^{- 1}$ is the backward shift operator, [ $a_{1 i} (t)$ ,…, $a_{m i} (t)$ ; $b_{0 i} (t)$ ,…, $b_{n i} (t)$ ; $c_{0 i} (t)$ ,…, $c_{p i} (t)$ ] are the parameters of the time-varying model, that are directly related to the parameters of EAS system.

4. Multi-model adaptive switching controller design

If the difference between the initial values of identifier in adaptive controller and the actual values of model parameters is too large, the convergence of identification process will need a long time, thus has an adverse impact on the control performance. Therefore, for control objects like EAS, whose parameters are easy to vary suddenly due to the change of driving conditions, the conventional adaptive controller can’t achieve a satisfying performance. This phenomenon and the better performace requirements above inspire to consider establishing multiple models according to the actual damping control process of EAS and choosing the proximate values of model parameters as the initial values of identifier, so the identification parameters can converge to the actual values quickly and the optimal control performance of adaptive controller can be guaranteed.

4.1. Establishment of the multiple models

From the analysis in Section 2, because of the influence of vehicle height adjustment, the air spring stiffness shows obvious time-varying and sudden change characteristics. Hence, to build the fixed model set for damping adaptive control, nine fixed full-car models of EAS system are considered to be established based on the variable stiffness of air spring, which are computed on the basis of the typical vehicle height modes and different load conditions in each height mode.

Combining with the following simulation in the next section, a EAS system which is used for limousine is chosen as the study object. The equivalent lengths of the four air springs in three vehicle height modes are 150 mm, 175 mm and 205 mm respectively, the cross-sectional area of the air spring is 0.018 m², the normal load of the front wheel is 630 kg, the normal load of the rear wheel is 510 kg and the polytrophic index is 1.3. Substituting these parameters into Eq. (6), we can obtain the air spring stiffnesses for different vehicle height modes and different load conditions. In each height mode, three load conditions are set, i.e. the overload condition (120 % × normal load), the normal load and the under load condition (80 % × normal load). The variable stiffnesses of the air spring in different conditions are shown in Table 1.

Table 1The air spring variable stiffnesses

Load condition	Height mode	Air spring stiffness (N/m)
Load condition	Height mode	$k_{f l}$	$k_{f r}$	$k_{r l}$	$k_{r r}$
Overload condition	Highway mode	65520	65520	53040	53040
	Normal mode	56160	56160	45463	45463
	Off-road mode	47941	47941	38810	38810
Normal load	Highway mode	54600	54600	44200	44200
	Normal mode	46800	46800	37886	37886
	Off-road mode	39951	39951	32341	32341
Underload condition	Highway mode	43680	43680	35360	35360
	Normal mode	37440	37440	30309	30309
	Off-road mode	31961	31961	25873	25873

The establishment of the fixed models can ensure the transient response speed of control, meanwhile, a adaptive model whose parameters’ initial values can be re-assigned is introduced to improve the control precision. The specific identification process of model parameters is described as follows:

Rewrite Eq. (12) as:

14

y (t) = - a_{1 i} (t) y (t - 1) - \cdot \cdot \cdot - a_{m i} (t) y (t - m) + b_{0 i} (t) u (t - 1)

+ \cdot \cdot \cdot + b_{n i} (t) u (t - n - 1) + c_{0 i} (t) w (t - 1) + \cdot \cdot \cdot + c_{p i} (t) w (t - p - 1),

15

y (t) = θ (t)^{T} ϕ (t - 1),

16

\{\begin{array}{l} θ (t)^{T} = [- a_{1 i} (t), \dots, - a_{m i} (t); b_{0 i} (t), \dots, b_{n i} (t); c_{0 i} (t), \dots, c_{p i} (t)], \\ ϕ (t - 1)^{T} = [\begin{matrix} y (t - 1), \dots, y (t - m); u (t - 1), \dots, u (t - n - 1); \\ w (t - 1), \dots, w (t - p - 1) \end{matrix}], \end{array}

Conduct parameters identification of Eq. (15) by using improved projection algorithm [17]:

17

\hat{θ} (t) = \hat{θ} (t - 1) + \frac{ϕ (t - 1) e (t)}{1 + ϕ (t - 1)^{T} ϕ (t - 1)},

where $\hat{θ} (t)$ represents the identification parameters and:

18

\{\begin{array}{l} e (t) = [y (t) - \hat{θ} (t - 1)^{T} ϕ (t - 1)], \\ {\hat{θ}}^{T} (t) = [- {\hat{a}}_{1 i} (t), \dots, - {\hat{a}}_{m i} (t); {\hat{b}}_{0 i} (t), \dots, {\hat{b}}_{n i} (t); {\hat{c}}_{0 i} (t), \dots, {\hat{c}}_{p i} (t)] . \end{array}

4.2. Model switching strategy

In order to choose the proximate model for the actual running states of EAS, the actual system outputs are considered to be compared with the outputs of the established multiple models, and a model switching performance index is proposed as follows:

19

J_{j} (t) = \sum_{k = 1}^{t} α (k)^{t - k} |y (k) - θ_{j}^{T} ϕ (k - 1)|, (j = 1, 2, \dots, 9; 0 < α < 1),

where $α$ is the weighted factor, $t$ is the computational time domain, and:

20

θ_{j} = [- a_{1 i}^{j} (t), \dots, - a_{m i}^{j} (t); b_{0 i}^{j} (t), \dots, b_{n i}^{j} (t); c_{0 i}^{j} (t), \dots, c_{p i}^{j} (t)] .

Because of the outputs of EAS have a big difference in the order of magnitude, so that they can’t be superposed as the performance index directly and the quantization processing in same scale must be conducted. The root mean square values of outputs in computational time domain is counted firstly, and then the same scaling coefficients are determined as:

21

{\ddot{z}}_{s} \times β_{1} = \ddot{θ} \times β_{2} = \ddot{φ} \times β_{3} = (z_{f l 1} - z_{f l}) \times γ_{1} = [k_{t} (z_{f l 0} - z_{f l})] \times η_{1},

where $β_{1 - 3}$ is the coefficients of vehicle body accelerations, $γ_{1}$ is the coefficient of suspension deflection and $η_{1}$ is the coefficient of dynamic wheel load.

After that, the model switching performance index can be rewritten as:

22

J_{j} (t) = \sum_{k = 1}^{t} α (k)^{t - k} |\bar{y} (k) - θ_{i}^{T} ϕ (k - 1)|,

where $\bar{y} (k)$ is the system outputs which have been quantitated in same scale. Thus, at each sampling time, the proximate model parameters can be got based on the performance index (Eq. 22) as follows:

23

j (t) = \arg (m i n \underset{1 \leq j \leq 9}{J_{j}} (t)),

and the model parameters are then assigned to the adaptive model, i.e. $\hat{θ} (t) = θ_{j (t)}$ .

4.3. Design of the adaptive controller

After getting the proximate model parameters, a adaptive controller is designed to achieve the optimal regulation of damping force and the following aspects are taken into consideration:

Define the auxiliary outputs for Eq. (12):

24

f (t) = P (q^{- 1}) A_{1} (q^{- 1}) y (t) + Q (q^{- 1}) u (t - 1) + R (q^{- 1}) w (t - 1),

where $P$ , $Q$ and $R$ satisfy the following relationship:

25

P (q^{- 1}) B (q^{- 1}) + Q (q^{- 1}) F (q^{- 1}) + Δ R (q^{- 1}) = 1,

where $Δ = 1 - q^{- 1}$ .

Now assume that there are two positive integers $L$ , $M$ are given, and $L \leq M$ . If function $σ (\cdot)$ is continuous and satisfy:

26

\{\begin{array}{l} s σ (s) > 0, (s \neq 0), \\ σ (s) = s, (|s| \leq L), \\ |σ (s)| = M, (|s| > L), \end{array}

then the function $σ (\cdot)$ is defined as the linear saturation function of $L$ and $M$ . Therefore, the nonlinear adaptive controller can be described based on the defined auxiliary outputs and the linear saturation function as:

27

u (t) = - σ_{k - 1} (Δ^{k - 1} f (t) + σ_{k - 2} (Δ^{k - 2} f (t) + \dots + σ_{0} (f (t) - r (t)) \dots),

where $σ_{i}$ is the linear saturation function for positive integers ( $L_{i}$ , $M_{i}$ ) ( $i =$ 0, 1,…, $k -$ 1), and the $L_{i}$ , $M_{i}$ are defined as:

28

\{\begin{array}{l} L_{i} \leq M_{i}, & i = 0, 1, \dots, k - 1, \\ M_{i} < 0.5 L_{i + 1}, & i = 0, 1, \dots, k - 2 . \end{array}

The goal we wish to achieve with the multi-model adaptive switching controller is to track the reference system outputs by controlling the adjustable damping force.

4.4. Stability of the controller

To set up the multi-model adaptive switching controller, some assumptions about the model of electronic air suspension system as Eq. (12) should be given first:

A1) The order of the model, i.e. $m$ , $n$ is known a priori;

A2) The vector of parameters [ $a_{1 i} (t)$ ,…, $a_{m i} (t)$ ; $b_{0 i} (t)$ ,…, $b_{n i} (t)$ ; $c_{0 i} (t)$ ,…, $c_{p i} (t)$ ] is piecewise constant (linear time variant, i.e. LTV system with jumping parameters) of sample time $t$ and changes in a compact set, in which $A_{1} (t, q^{- 1})$ is guaranteed stable, i.e. $A_{1} (t, q^{- 1}) \neq$ 0.

Theorem 1. When multi-model adaptive switching control strategy is applied to LTV system with jumping parameters, the switching of model will stop at an adaptive model after finite sample time and the closed-loop system is bounded-input bounded-output (BIBO) stable, the output of system will track set-point value $r (t)$ asymptotically.

Before the proof of Theorem 1, a lemma, which has been proved in [18], is given first.

Lemma 1. Parameter identification algorithm as Eq. (17) have the following properties to LTV system with jumping parameters:

1) $‖\hat{θ} (t) - θ‖ \leq ‖\hat{θ} (t - 1) - θ‖ \leq ‖\hat{θ} (0) - θ‖$ , $t \geq$ 1;

2) $\underset{t \to \infty}{l i m} ‖\hat{θ} (t) - \hat{θ} (t - k)‖ = 0$ , for any finite integer $k$ ;

3) $\underset{t \to \infty}{l i m} \frac{e (t)}{[1 + ϕ (t - 1)^{T} ϕ (t - 1)]^{1 / 2}} = 0$ , where $e (t) = \bar{y} (t) - \hat{θ} (t - 1)^{T} ϕ (t - 1)$ .

The proof of Theorem 1. When multi-model adaptive control is applied to LTV system with jumping parameters, we can find that the control system is input bounded from Eq. (27), from A2), it can be seen that the system output $y (t)$ is bounded. According to Eq. (14), we know that $ϕ (t - 1)$ is bounded. From 3) of Lemma 1 and Lemma 6.2 of [18], the following conclusions can be got as:

29

\underset{t \to \infty}{l i m} [\bar{y} (t) - \hat{θ} (t - 1)^{T} ϕ (t - 1)] = 0 .

From Eq. (22) and Eq. (23), we know that the model switching will stop at an adaptive model, and:

30

\underset{t \to \infty}{l i m} e (t) = \underset{t \to \infty}{l i m} [\bar{y} (t) - \hat{θ} (t - 1)^{T} ϕ (t - 1)] = 0 .

The parameter will converge finally according to Eq. (23) and 1), 2) of Lemma 1, from Theorem 2.3 of [19], adaptive controller will make the output of system:

31

A_{1} (t, q^{- 1}) y (t) = B_{1} (t, q^{- 1}) u (t - 1) + C_{1} (t, q^{- 1}) w (t - 1),

track $r (t)$ asymptotically. Thus the multi-model adaptive control can make the output of LTV system with jumping parameters track $r (t)$ asymptotically.

Remark 1. From Theorem 1, we can see that the multi-model adaptive controller can keep the system stability and convergent property of conventional adaptive control algorithm when it is applied to LTI (linear time invariant) system or LTV system with jumping parameters. At the same time, because of the existence of multiple models, the convergent identification speed of system parameters is speed up and the transient response is improved effectively. An LTV system with jumping parameters can be considered as an LTI system in the interval of the two adjacent parameter jumping. According to Theorem 1, when the interval is sufficiently long, the closed-loop system is also BIBO stable. Therefore, the multi-model adaptive controller can also improve the control performance of LTV discrete time system with jumping parameters.

5. Simulation results and discussion

To analyze the performance of the multi-model adaptive switching controller described in this paper, we will compare it against the original adaptive controller. Two typical simulation conditions, which fit the actual vehicle driving states, are designed as Table 2 to verify the effectiveness of the proposed control algorithm.

Reviewing the information of the two simulation conditions, we observe that the condition A is designed for the vehicle height general adjustment, while the condition B is designed for the vehicle height stable adjustment. These two conditions can verify the identification ability of the control algorithm when sudden change of the EAS system parameters happened. For our simulation, the other fixed model parameters are selected as Table 3.

Table 2Typical simulation conditions

Simulation condition	Simulation time/s	Road classification	Vehicle speed/(km.h^-1)	Vehicle height mode	Load condition
Condition A	0-5	C	60	Normal	Normal
	5-10	B	100	Highway	Normal
	10-15	E	20	Off-road	Normal
Condition B	0-5	C	60	Normal	Normal
	5-10	C	60	Normal	Overload
	10-15	C	60	Normal	Underload

Table 3System parameters

Two wheels distance in meters	1.63	Tire stiffness in kN/m	192
C.G. to front axle distance in meters	1.45	Front suspension base damping in N·s/m	1460
C.G. to rear axle distance in meters	1.69	Rear suspension base damping in N·s/m	1570
Front wheel unsprung mass in kilograms	120	Roll moment of inertia in kg·m²	679
Rear wheel unsprung mass in kilograms	90	Pitch moment of inertia in kg·m2	2304

The simulation is run utilizing the road profile of a random base excitation with different road class roughness. The vehicle is driven with a constant speed and the time histories data of road irregularity are described by power spectral density (PSD) method [20]. The simulation results of the two conditions are charted in Fig. 4, Fig. 5 and Table 4. We can easily identify that the performance difference between the original adaptive controller (OAC) and the multi-model adaptive switching controller (MASC) is tiny during 0-5 s, only slight difference due to the randomness of linear saturation function exist. This can be explained by the fact that the initial values of the air spring stiffness is set as same as the actual values for simulation, thus the model parameters of the both two control methods can converge quickly. At 5 s and 10 s, which are the sudden change time of vehicle driving condition, we can see that the MASC is superior in performance over the OAC in the initial stage, that’s due to the OAC can’t converge the model parameters quickly, while the MASC can switch to the proximate model according to the switching index, thus achieve the better control performance.

Fig. 4Simulation results of condition A

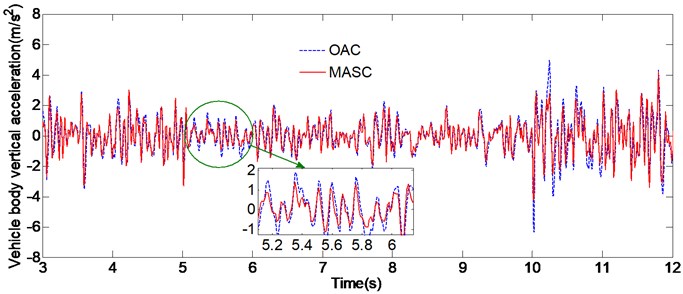
a) Vehicle body vertical acceleration

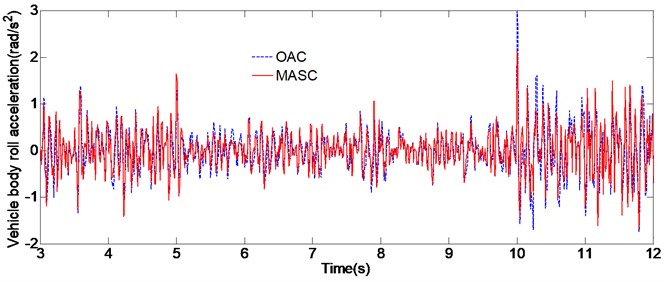
b) Vehicle body roll acceleration

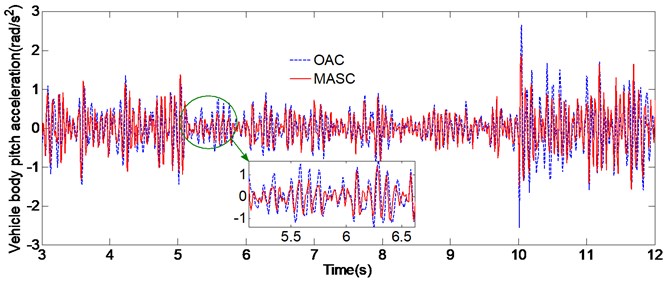
c) Vehicle body pitch acceleration

Table 4RMS acceleration comparison and reduction (RED)

Condition	Time/s	Vertical acceleration (m/s²)			Roll acceleration (rad/s²)			Pitch acceleration (rad/s2)
Condition	Time/s	OAC	MASC	RED	OAC	MASC	RED	OAC	MASC	RED
Condition A	3-5	1.29	1.31	–1.5 %	0.82	0.79	2.4 %	0.85	0.83	2.3 %
	5-7	0.72	0.63	12.5 %	0.57	0.46	19.3 %	0.52	0.41	21.1 %
	7-10	0.64	0.65	–1.6 %	0.48	0.49	–2.1 %	0.43	0.44	–2.3 %
	10-12	2.24	1.96	13.1 %	1.59	1.41	10.7 %	1.87	1.69	9.6 %
	12-15	1.92	1.91	0.52 %	1.45	1.43	1.3 %	1.71	1.68	1.7 %
Condition B	3-5	1.32	1.33	0.75 %	0.92	0.94	–2.2 %	0.84	0.85	–1.2 %
	5-7	1.47	1.32	10.2 %	1.07	0.92	13.8 %	0.79	0.68	13.9 %
	7-10	1.35	1.34	0.74 %	0.94	0.95	–1.1 %	0.72	0.70	2.8 %
	10-12	1.27	1.14	10.2 %	0.86	0.76	11.8 %	0.75	0.63	16 %
	12-15	1.13	1.14	0.88 %	0.78	0.76	2.5 %	0.62	0.60	3.2 %

Fig. 5Simulation results of condition B

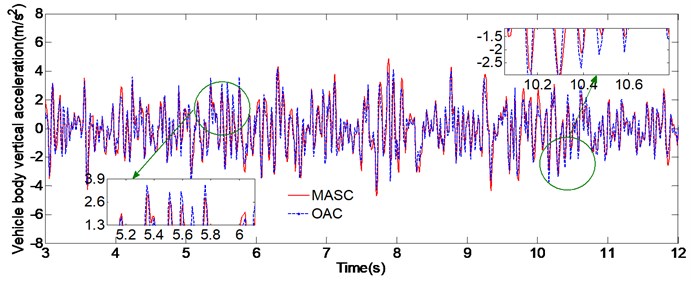
a) Vehicle body vertical acceleration

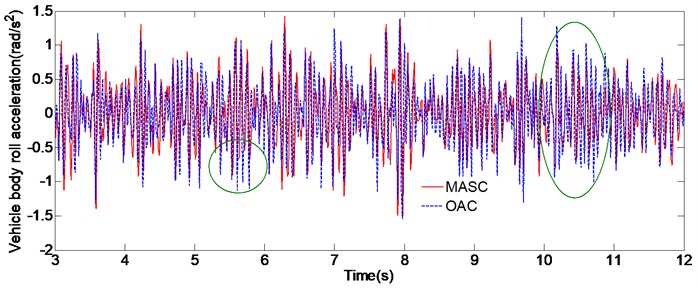
b) Vehicle body roll acceleration

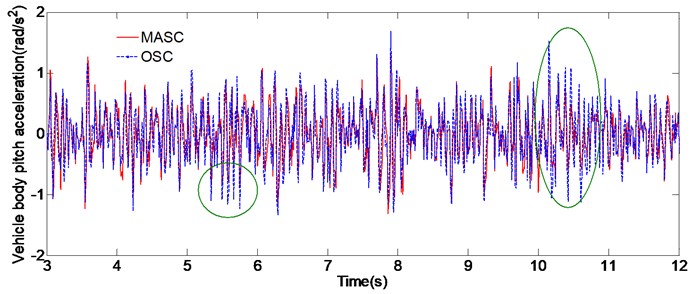
c) Vehicle body pitch acceleration

6. Conclusions

In this paper it has been discussed about the designing of a novel damping force controller based on multi-model adaptive switching control strategy for EAS system. The multiple system models with fixed parameters and an adaptive model whose initial value of parameters can be re-assigned are established based on the full-car dynamics. Performance simulation is conducted by Matlab/Simulink and the performance comparisons between the original adaptive controller and the multi-model adaptive switching controller are done. The results prove that the EAS system with multi-model adaptive damping controller can improve the ride comfort when sudden change of driving conditions happened, which show the effectiveness of the multi-model adaptive switching control framework for solving the damping control problem of EAS system

References

Du Haiping, Sze Kam Yim, Lam James Semi-active H_∞control of vehicle suspension with magneto-rheological dampers. Journal of Sound and Vibration, Vol. 283 Issues 3-5, 2005, p. 981-996.

Search CrossRef
Hyundong H., Suh Jeeyoon, Yi Kyongsu Integrated control of the differential braking, the suspension damping force and the active roll moment for improvement in the agility and the stability. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol. 229, Issue 9, 2015, p. 1145-1157.

Search CrossRef
Prabakar R. S., Sujatha C., Narayanan S. Optimal semi-active preview control response of a half car vehicle model with magnetorheological damper. Journal of Sound and Vibration, Vol. 326, Issues 3-5, 2009, p. 400-420.

Search CrossRef
Mehdi Fateh Mohammad, Sina Alavi Seyed Impedance control of an active suspension system. Mechatronics, Vol. 19, Issue 1, 2009, p. 134-140.

Search CrossRef
Haiping Du, Nong Zhang H_∞control of active vehicle suspensions with actuator time delay. Journal of Sound and Vibration, Vol. 301, Issues 1-2, 2007, p. 236-252.

Search CrossRef
Han Shi Yuan, Tang Gong You, Chen Yue Hui, Yang Xi Xin, Yang Xue Optimal vibration control for vehicle active suspension discrete-time systems with actuator time delay. Asian Journal of Control, Vol. 15, Issue 6, 2013, p. 1579-1588.

Search CrossRef
Crews John H., Mattson Michael G., Buckner Gregory D. Multi-objective control optimization for semi-active vehicle suspensions. Journal of Sound and Vibration, Vol. 330, Issue 23, 2011, p. 5502-5516.

Search CrossRef
Kim Hyunsup, Lee Hyeongcheol Height and leveling control of automotive air suspension system using sliding mode approach. IEEE Transactions on Vehicular Technology, Vol. 60, Issue 5, 2011, p. 2027-2041.

Search CrossRef
Xu Xing, Chen Long, Sun Liqin, Sun Xiaodong Dynamic ride height adjusting controller of ECAS vehicle with random road disturbances. Mathematical Problems in Engineering, Vol. 2013, 2013, p. 1-9.

Search CrossRef
Xiao Jie, Kulakowski Bohdan T., Cao Ming Active air-suspension design for transit buses. International Journal of Heavy Vehicle Systems, Vol. 14, Issue 4, 2007, p. 421-440.

Search CrossRef
Yin Zhihong, Khajepour Amir, Cao Dongpu, Ebrahimi Babak, Guo Konghui A new pneumatic suspension system with independent stiffness and ride height tuning capabilities. Vehicle System Dynamics, Vol. 50, Issue 12, 2012, p. 1735-1746.

Search CrossRef
Peng Zhouhua, Wang Dan, Zhang Hongwei, Sun Gang, Wang Hao Distributed model reference adaptive control for cooperative tracking of uncertain dynamical multi-agent systems. IET Control Theory and Applications, Vol. 7, Issue 8, 2013, p. 1079-1087.

Search CrossRef
Annamala A. S. K., Sutton R., Yang C., Culverhouse P., Sharma S. Robust adaptive control of an uninhabited surface vehicle. Journal of Intelligent and Robotic Systems, Vol. 78, Issue 2, 2015, p. 319-338.

Search CrossRef
Lee S. J. Development and analysis of an air spring model. International Journal of Automotive Technology, Vol. 11, Issue 3, 2010, p. 471-479.

Search CrossRef
Kim Hyunsup, Lee Hyeongcheol Fault-tolerant control algorithm for a four-corner closed-loop air suspension system. IEEE Transactions on Industrial Electronics, Vol. 58, Issue 10, 2011, p. 4866-4879.

Search CrossRef
Marzbanrad J., Poozesh P., Damroodi M. Improving vehicle ride comfort using an active and semi-active controller in a half-car model. Journal of Vibration and Control, Vol. 19, Issue 9, 2013, p. 1357-1377.

Search CrossRef
Wang H., Xu G., Zhang S., Yan W. An implementation of generalized back projection algorithm for the 2-D anisotropic EIT problem. IEEE Transactions on Magnetics, Vol. 51, Issue 3, 2015, p. 1-4.

Search CrossRef
Goodwin G. C., Sin K. C. Adaptive Filtering Prediction and Control. Prentice Hall, Englewood Cliffs, 1984.

Search CrossRef
Zhu K. Y., Wang L. Design of stable linear system with input constrain. IFAC 5th Symposium on Low Cost Automation, Shenyang, 1998.

Search CrossRef
Dodds C. J., Robson J. D. The description of road surfaces roughness. Journal of Sound and Vibration, Vol. 31, Issue 2, 1973, p. 175-183.

Search CrossRef

About this article

Received

08 June 2015

Accepted

28 August 2015

Published

30 September 2015

SUBJECTS

Vibration in transportation engineering

Keywords

electronic air suspension

damping control

multi-model adaptive switching control

full-car model

Acknowledgements

Research work has been partly supported by National Natural Science Foundation of China (Grant No. 51375212), A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20133227130001), and China Postdoctoral Science Foundation (Grant No. 2014M551518).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.