The study of damping control in semi-active car suspension

1. Introduction

The suspension issue was already considered in the times of horse-drawn carriages. Just as in power units, a tremendous progress has been done in the field of suspensions. Recent designs of suspensions are often advanced systems utilizing a range of sensors. Today’s vehicles, achieving considerable values of speed, have to guarantee, beyond comfort, a good handling what is needed to fulfill safety requirements.

The suspension’s objectives can be formulated as follows [1]:

– transmission of static and dynamic forces at the tyre/road contact;

– insulation of the car’s chassis from kinetic’s input function, as an effect of a road shape, which causes dynamic forces and undesirable oscillations;

– reduction of the operational displacements of the suspension system.

For many years simultaneous improvement in the range of comfort and handling was constrained by the constant parameters of damping in shock absorber. It was feasible to design a vehicle with very good handling but uncomfortable (e.g. sports cars) and vice versa. The sophisticated issue is complicated due to a change of the sprung mass in dependence of current vehicle’s load.

This intuitive contradiction between mentioned suspension’s features is depicted in Fig. 1. As it is visible a concurrent enhancement of both parameters is unviable. This dependence, as discussed in many papers (e.g. in [2-4]), however intuitive, is not fully true.

In [5] the author proved that the dependence of comfort and handling parameters in some ranges of damping can be consistent. Fig. 2 presents a graph showing values of two parameters introduced by the authors. Namely, WP1 related to comfort and WP2 associated with handling. In both cases, the higher is the value, the better performance is obtained. On the $X$-axis is indicated a relative damping coefficient GAMT [–], defined as follows [5]:

where $m_1$ – sprung vehicle’s mass; $c_{1kr}$ [N∙s/m] – critical damping coefficient; ${\omega }_{01}=2\pi f_{01}$ – the first (lower) natural radian frequency of the undamped system [rad/s].

As can be seen in the Fig. 2, there are ranges, in which WP1 and WP2 consistently grow (GAMT from 0.1 to 0,25) and fall (GAMT from 0.4 to 0.6) what is fundamentally incompatible with Fig. 1.

Fig. 1Ideological shape of dependence between the comfort and safety requirements at the selection of constant damping in the suspension system [2].

Fig. 2Comfort indicator WP1 and safety indicator WP2 vs. relative damping coefficient, for the road of average quality according to the ISO standard and for 4 vehicle speed values ranging from 30 km/h to 120 km/h [5]

The perpetual struggle of cars’ manufacturers to enhance comfort and handling of their cars, motivated by customers’ expectations, leads to implementation of new solutions of suspensions. The breakthrough came with the deployment of active and semi-active suspensions [1, 2]. More complicated and expensive active suspensions were introduced first by hydro-pneumatic solution of Citroen in 1954 [6], whereas semi-active suspension was presented only in 70’ [7]. Fig. 3 compares all three types of suspension.

Passive and semi-active systems can only dissipate and store energy. In passive suspensions there are (nearly) constant values of damping and spring stiffness, set during manufacturing process. Those values are a compromise between comfort, handling and predicted changes of sprung mass, as a result of car’s authorized payload.

In semi-active suspensions shock-absorber has a variable damping coefficient, which in dependence of design’s advancement can have two or several stages of damping or may change continuously. This change of damping can be done on driver request (e.g. sport/comfort mode) or in autonomous way, based on set of sensors which are employed to on-line analysis of the road profile.

Active suspensions are equipped with an actuator, capable of adding energy to the suspension. In this case, a change of chassis height relative to the road is possible and the change of suspension stiffness as well. An indisputable drawback of this system, apart from already mentioned complexity and priciness, is high power consumption. According to [2] peak power achieves up to 4 kW. For this reason, this type of suspension is mainly used in luxurious cars.

In the long term it turned out that the active suspensions are complicated, expensive in manufacturing and service for customers. The Golden Mean seems to be a semi-active suspension, which has better performance than classical (passive), and simultaneously is much simpler and cheaper than the active one.

The change of shock-absorber’s damping characteristic can be realized in three ways:

– with the use of magneto-rheological (MR) fluids. Their properties change in dependence of a controlled magnetic field [8, 9];

– with the use of electro-rheological (ER) fluids. Their properties change in dependence of controlled electric field [10, 11];

– employing controlled valves, installed in the connection line between two sites of the piston in the oil-filled damper [12, 13].

Fig. 3Suspension systems classification [2]

a) Passive suspension

b) Semi-active suspension

c) Active suspension

2. Damping control proposal

According to mentioned semi-active suspension merits and active suspension drawbacks, authors of this paper focused on the first type. It seems that nowadays such suspensions have greater potential to achieve popularity among vehicles of different than luxurious classes.

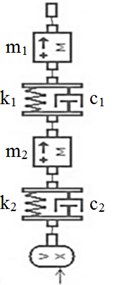
In the Fig. 4, a classical two-mass quarter car model is presented, whereas pros and cons of this model are detailed in [14], where $m_1$ – sprung vehicle’s mass, $m_2$ – unsprung wheel’s mass, $k_1$ – suspension spring’s stiffness coefficient, $k_2$ – wheel’s radial stiffness, $c_1$ –damper’s viscous coefficient, $c_2$ – wheel’s damping coefficient, $x$ – chassis’ vertical motion coordinate, $y$ – wheel’s vertical motion coordinate, $z$ – kinematic excitation from road.

The equations of forces will be:

According to Newton’s law the accelerations of both masses will be:

Semi-active suspensions have gained a lot of attention, thanks to their controllable parameters that can be adjusted in real time [15-17]. Damper force tracking control strategies has been developed based on feedforward or feedback linear or non-linear models [18, 19]. These solutions demand a current damper force or complex damper model.

Fig. 4Vehicle’s two-mass quarter car model [5]

In line with common practice (e. g. in [20-22]), three criteria can be distinguished to assess the correctness of the suspension damping coefficient $c_1$:

– the minimization of oscillations (vertical accelerations) of vehicle’s sprung mass- a parameter particularly important for passengers and carried load;

– minimization of dynamic deviation of the vertical component of the reaction at the tyre/road contact. The aim is to keep the value possibly close to the static one;

– limitation of the working displacements of the suspension system.

In this study the first criterion, concerning passengers comfort was chosen. On the basis of the Eq. (2), the following rule can be found: When both terms of the equation (connected respectively with damping and elasticity) take the same signs it causes the summation of forces acting on a chassis and thereby increase of accelerations is observed. If the damping coefficient is minimized, a decrease of the force $F_{yx}$ and acceleration will be observed.

The second remark which comes from Eq. (2) is that when both terms of the equation take opposite signs, there is a theoretical possibility (by continuous change of damping) to neutralize forces acting on a chassis, so accelerations too.

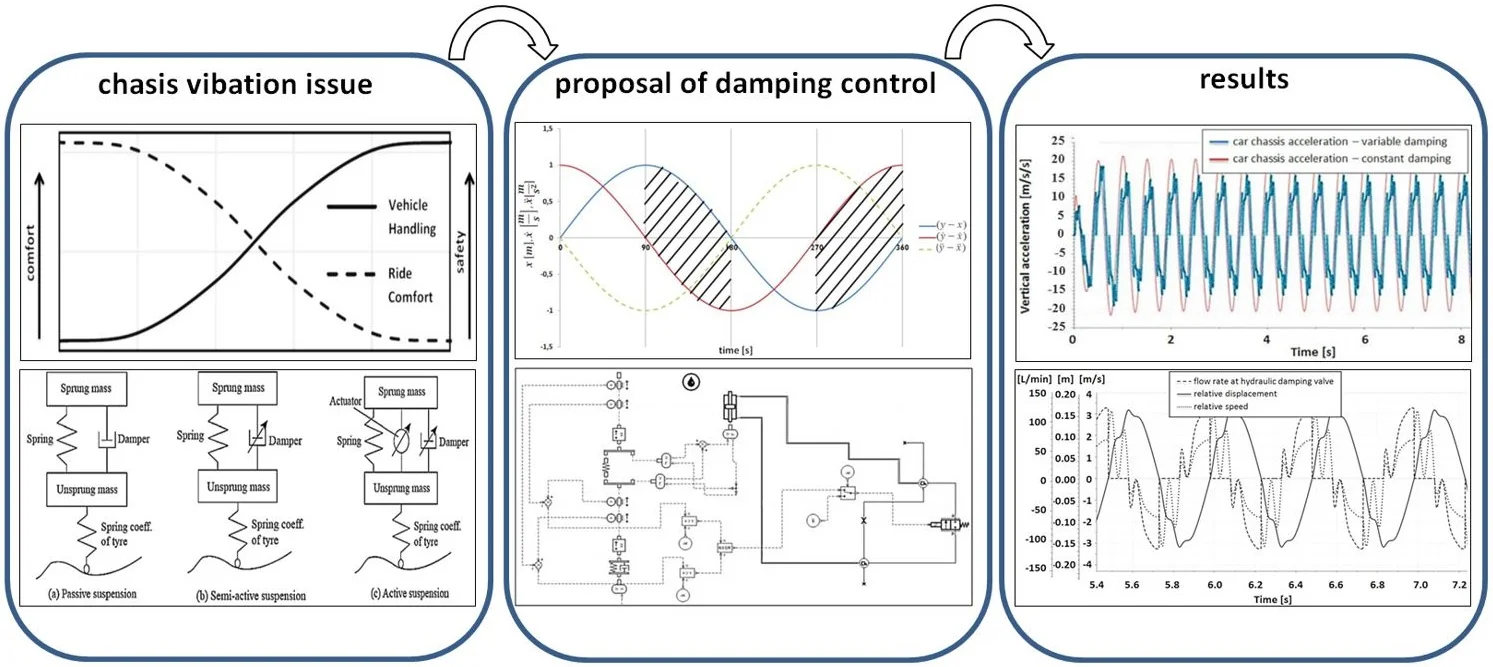
On the grounds of the perceived principles, a proposal of damping control strategy in semi-active car suspension was created. It’s major aim was chassis’ acceleration reduction, as compared to the classical passive suspension. The main principle in the control strategy is to provide minimal value of damping when both terms of the Eq. (2), connected with damping and elasticity, have the same signs, respectively. When they have opposite signs, the high value of damping will be obtained.

Periods when both terms of the Eq. (2) have different signs, (the example concerns sinusoidal excitation) are depicted in Fig. 5 and hatched – in those moments damping should be high.

To implement the proposed control strategy of damping, it is necessary to catch the value of relative displacement between the chassis and the wheel, so the term $(y-x)$. It can be deduced from the movement of the shock absorber starting from a neutral position. The only matter to overcome is to find the coordinate of this neutral position because it varies with the current vehicle’s load [1]. It can be checked and set during every stop of a car- for example while waiting at traffic lights. If the term $(y-x)$ is known, the first derivative $(\dot{y}-\dot{x})$can be determined.

Comparing to the solutions described in the literature [15-19], the control system presented in this paper seems to be simpler because it only requires the knowledge of signs of the both terms of the Eq. (2). Moreover, the novelty of this approach is that there is only one executive element to control the damping coefficient.

Fig. 5Periods when damping coefficient should be high- hatched areas

3. Model test results and discussion

Simulation was done with use of Amesim [23] software. The tests were carried out simultaneously for two suspension models. The first one was a classical two-mass quarter car model being a reference and the second one, representing the new suspension concept.

The parameters of vehicle’s suspension can be noticeably different in dependence of car’s purpose. After studying literature (including [24-26]), authors assumed the following parameters of two-mass quarter car model (Table 1).

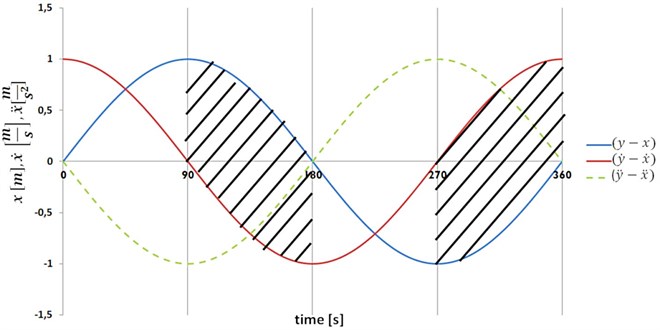
Fig. 6Two types of input signal used in the simulation model

Two types of input signal (Fig. 6) came from the same source and was divided in two branches to be sure that both models have the same excitation. The variable sinusoidal signal had constant amplitude of 0.1 m and the frequency, which changed from 0.5 Hz to 2.5 Hz with a slope of 0.2 Hz/s. The simulation models are shown in Fig. 7. The standard damper was substituted by a hydraulic actuator and an additional damping valve, therefore the damping force could be varied.

The assumed geometry of the hydraulic actuator is presented in Fig. 8.

Fig. 7Suspension models: a) classical damper, b) hydraulic damper model

a)

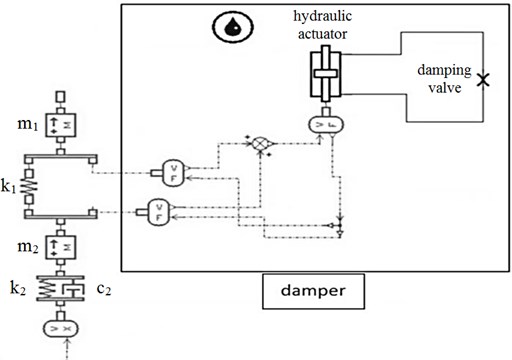
b)

Fig. 8Actuator used instead of classical damper

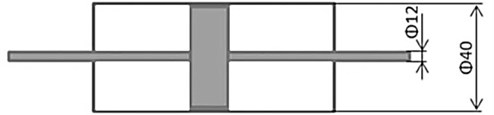
An additional damping valve was used to create a controllable damping effect. There are five models to define the pressure drop on the valve in Amesim software. One of them is to define the characteristic flow rate and corresponding pressure drop. Suitable choice of the valve characteristics allowed obtaining damping which was similar to the classical suspension. Therefore, necessary calculations were done.

Active area ($A$) of actuator:

The idea was to have damping coefficient equal to 2200 N/(m/s). It means, that if the actuator’s rod moves with linear speed $V=$ 1 m/s the drag force ($F$) should achieve 2200 N. So the characteristic flow rate (CHFR) can be calculated as follows:

and the corresponding pressure drop (CPD) can be expressed by:

The response of the car’s chassis on the variable sinusoidal signal and step signal for both models is presented in the Fig. 9.

Fig. 9Car body vibration depending on the model and different excitations: a) variable sinusoidal signal; b) step function

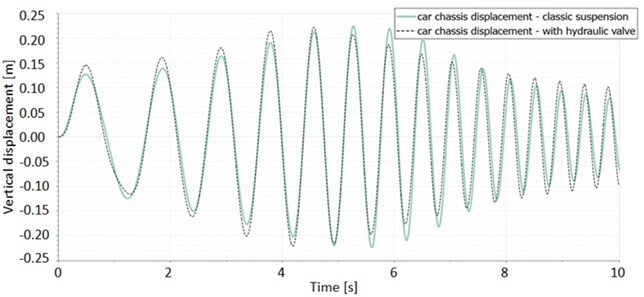
a)

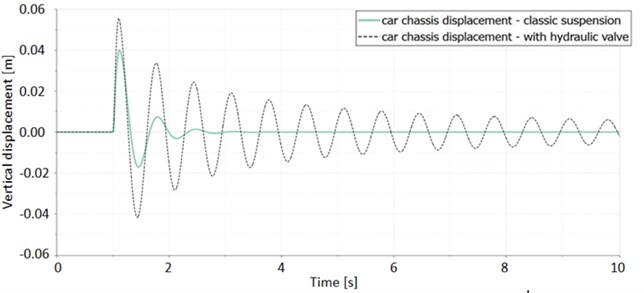
b)

Fig. 10Car’s chassis response for both models of suspension for the same step excitation

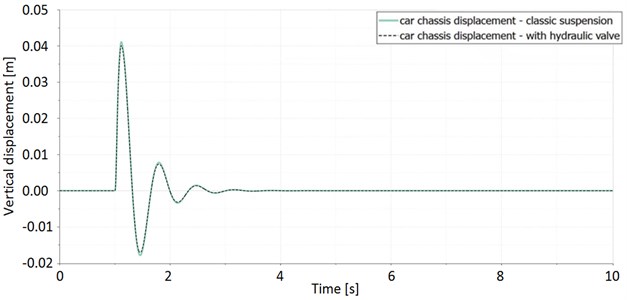
It can be noticed that the model with hydraulic actuator and valve do not correspond with the damper used at the classic suspension. The reason for it is that the classic suspension (damper in Amesim software) has linear dependence between the speed and damping force while this of a new concept is suspected to have another one. In the hydraulic actuator model defined in Amesim there is a parameter called critical flow number (CFL). Default CFL value is set to 1000. If the current value of the oil flow is less than CFL, the flow is laminar, if it is higher than this threshold, the oil flow is modelised as a turbulent. If we increase the value of the threshold 1000 times, we can assume that the oil flow in the actuator will be ever laminar. Fig. 10 shows the results obtained for CFL equal to 1 million. Now the curves representing car body vibration for both models are the same.

The next step was to introduce the possibility of turning on and off the damper. The new model is presented in the Fig. 11.

Fig. 11Model with controllable bypass valve

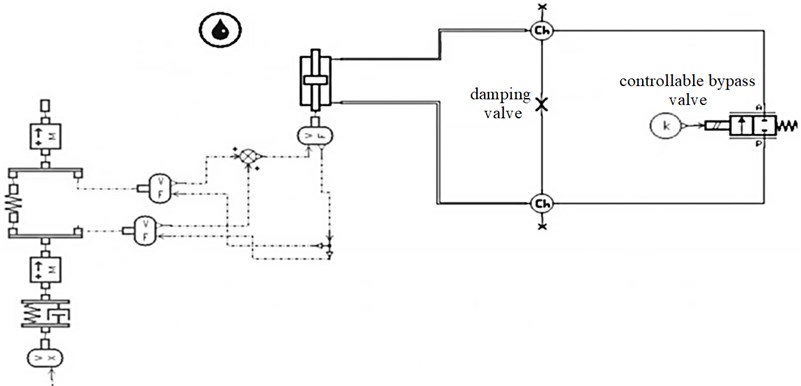
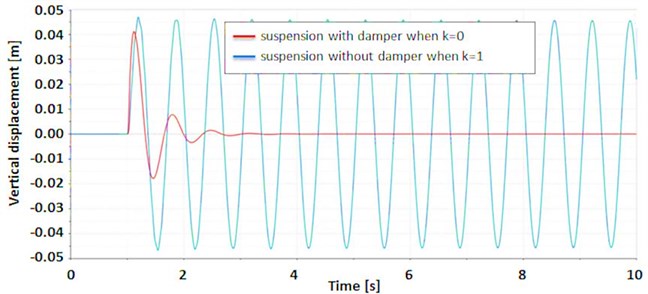
A controllable bypass valve was connected in parallel to the damping valve. When the bypass valve was open ($k=$1) almost all fluid flowed through the controllable valve and there was no damping effect. When the bypass valve was closed ($k=$0) the fluid flowed through the damping orifice and there was a damping effect. The results for both cases, closed ($k=$0) and open ($k=$1) valve are shown in the Fig. 12.

Fig. 12The results for closed (k= 0) and open (k= 1) controllable valve

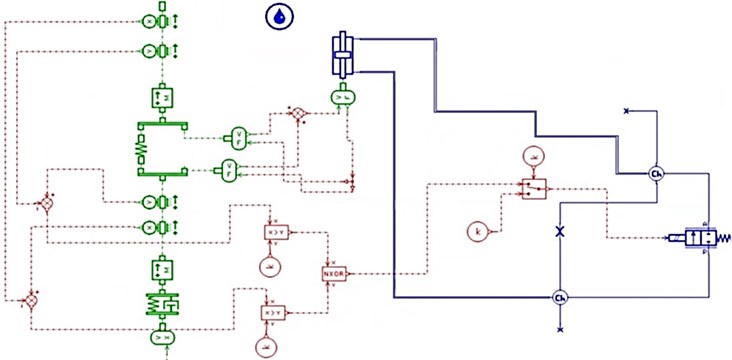
Finally, the proposed control system, described in the second chapter was introduced. To implement the proposed damping control strategy, it was necessary to catch the value of relative displacement between the vehicles’ chassis and the wheel. Therefore, the displacement and speed were measured at both spring ends and used as a control signals (Fig. 13).

Fig. 13Model with proposed damping control system

The response of both models (classic suspension and suspension with controlled damping) on the sinusoidal excitation is presented in Fig. 14. It can be noticed that car’s chassis displacements as well as accelerations values are smaller than for classical damping.

Fig. 14Car’s chassis response on sinusoidal excitation: a) displacement; b) acceleration

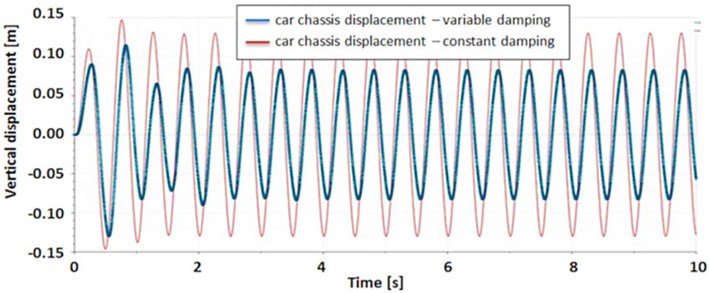
a)

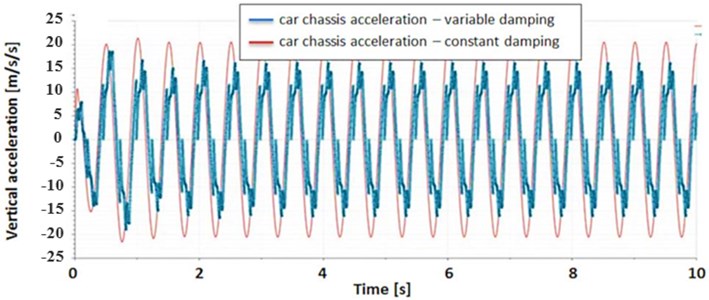
b)

The parameters of the operation of the control system are presented in the Fig. 15. Damping valve is open and oil flows through it (dashed line) only when the sign of relative displacement (solid line) is opposite to the sign of relative speed (dotted line). Relative displacement and speed are measured between car’s chassis and wheel.

It has to be emphasized that the presented graphs and promising results originate from the simulation only. Undoubtedly it has to be verified in the laboratory conditions. Therefore, a new test stand has been manufactured and optimized to determine the vehicles chassis accelerations caused by varied road profiles. The main problem is to design a solenoid valve (bypass) which allows to introduce immediate changes in the damping coefficient from 2200 N/(m/s) to almost zero and conversely. Acquirement of such beneficial results from real objects is the main goal of further work to be done within this project.

Fig. 15The performance of the control system

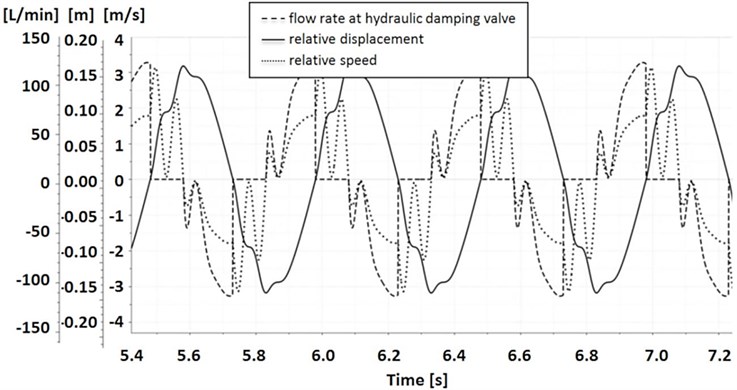
4. Conclusions

The proposed strategy of damping control seems to be an interesting idea because of its simplicity and no need of (noticeable) additional energy to drive any pump or accessory electric motor. Only the knowledge of terms’ signs of the Eq. (2) is required.

Presented results show that there is a justification for further development of this solution. Based on Fig. 14, comparing the amplitudes of vertical car’s chassis acceleration values, more than 20 % advancement is obtained. As mentioned in the Chapter 2, reduction of this parameter was assumed as being principal from the passengers’ comfort point of view.

Further action will concern the detailed algorithm of switching the damping coefficient, to avoid any jerks which may be felt by the driver.

Validation of the efficiency of the proposed damping control strategy will be executed by comparison of vertical accelerations of the proposed suspension and classical passive suspension obtained through the scanned profile of the real road’s section.

The paper presents an example of discrepancy in test results to which can lead the indiscriminate accepting of default values of parameters in modeling software. This example is featured to draw the attention of researchers to potential source of mistakes.