Sensitivity of dynamic response of a clamped functionally graded magneto-electro-elastic plate to its elastic parameters

1. Introduction

More and more scholars invested research on the behaviors of magneto-electro-elastic structures employed as these smart or intelligent materials have the behavior of converting energy from one form to the other (among magnetic, electric and mechanical energy) (Nan, 1994; Harshe et al., 1993). For the purpose of design, optimization and inverse technique of these sensors, actuators, transducers and many other emerging components consists of magneto-electro-elastic materials, it is a strong significant for these smart or intelligent materials to study their dynamic characteristics by theories or techniques. Static and dynamic behavior of plates as well as infinite cylinder has been studied in the literature. Yu Pang et al. (2014) investigated dispersive behavior and band structure of SH waves in magnetic-electric (ME) periodically layered plate by the transfer matrix method. F. Moleiro et al. (2015) provides an assessment of layerwise mixed models using least-squares formulation for the coupled electromechanical static analysis of multilayered plates. G. Giannopoulos et al. (2007) solve the thermal, electrical, mechanical coupled mechanics problem for initial buckling analysis of smart plates and beams by discrete layer kinematics. M. Saadatfar and M. Aghaie-Khafri (2014) investigated static behavior of a functionally graded magneto- electro-elastic hollow sphere subjected to hydrothermal loading in the spherically symmetric state. The dynamic response of a rotating radically polarized functionally graded piezoelectric hollow cylinder is studied by A. H. Akbarzadeh and Z. T. Chen (2011). Jianke Du and Kai Xian et al. (2009) studied analytically SH surface acoustic wave propagation in a cylindrically layered piezomagnetic /piezoelectric structure. Buchanan (2004) used finite element method to study the behavior of layered versus multiphase magneto-electro-elastic infinite long plate composites. Wang et al. (2003) has carried out analysis of multilayered magneto-electro-elastic plates for mechanical and electrical loading by the state vector approach. Yansong Li and Jingjun Zhang (2014) investigated free vibration of a magneto-electro-elastic plate resting on a Pasternak foundation by Mindlin theory parameters. Rajesh K. Bhangale and N. Ganesan (2005) investigated free vibration of simply supported non-homogeneous functionally graded magneto-electro-elastic finite cylindrical shells. The studies on sensitivity of dynamic response of the functionally graded magneto-electro-elastic structure to its material parameters are less in the literature. In the present study, dynamic response sensitivity analysis of a clamped functionally graded magneto-electro-elastic plate to its elastic parameter is useful for the optimization designs and inverse techniques of smart materials.

2. Basic equations

The coupled constitutive equations for magneto-electro-elastic materials can be written as:

where $\mathbf{\sigma }$ denotes stress vector, $\epsilon$ denotes strain vector, $\mathbf{D}$ and $\mathbf{E}$ are, respectively, the electric displacement and field vector, $\mathbf{B}$ and $\mathbf{H}$ are the magnetic flux and induction vector. $\mathbf{C}$, $\mathbf{g}$, $\mathbf{\mu }$ are the elastic, dielastic permeability coefficients matrices. $\mathbf{e}$, $\mathbf{q}$ and $\mathbf{\alpha }$ are piezoelectric, piezomagnetic and magneto-electric induction coefficients matrices.

The strain-displacement relations are given by:

where $u$, $v$ and $w$ are, respectively, the displacements in the coordinate $x$, $y$ and $z$ directions.

The electric field is related to the electric potential as follows:

The relations between magnetic field and magnetic potential are given by:

3. Dynamics differential equation

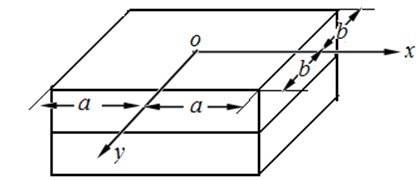
The functionally graded material parameters are assumed to obey polynomial law in the thickness direction. The plate is divided into 3 nodal surfaces namely upper, middle and lower nodal surfaces in the thickness $z$ direction. The mechanic model of the FGM magneto-electro-elastic plate is shown in Fig. 1.

For a clamped functionally graded magneto-electro-elastic plate, the generalized displacement functions of the plate are approximated as follows:

where ${\mathbf{N}}_d\left(z\right)$ is the shape function vector across the thickness direction of the plate:

where $N_1=\left(1-3\stackrel{-}{z}+2{\stackrel{-}{z}}^2\right)\text{,}$$N_2=4\left(\stackrel{-}{z}-{\stackrel{-}{z}}^2\right)\text{,}$$N_3=\left(2{\stackrel{-}{z}}^2-\stackrel{-}{z}\right)\text{,}$$\stackrel{-}{z}=\left(h-z\right)/h\text{,}$$h$ is the thickness of the plate.

Fig. 1Mechanic model of FGM magneto-electro-elastic plate

In Eq. (5):

where subscript ‘1’ denotes upper nodal surface, ‘2’ middle nodal surface and ‘3’ lower nodal surface.

The functional for piezoelectric-piezomagnetic-elastic materials can be written by:

where $q$ is the distribution force applied on the top surface of the plate, $\mathbf{u}$ is the elastic displacement:

${\mathbf{D}}_z$ and ${\mathbf{B}}_z$ are, respectively, the nodal electric displacement and magnetic flux vectors in the $z$ direction, given as follows:

Applying the variational principle $\delta \mathrm{\Pi }=0$ on Eq. (8), we obtained the coupled equations of the plate as follows:

where:

In Eq. (12):

In Eq. (13):

In Eq. (14):

In Eq. (15):

In Eq. (18):

In Eq. (19):

where:

If a harmonic mechanical excitation ${\mathbf{F}}^T=\left[\begin{array}{lllllllll}0& 0& 0& 0& 0& 0& 0& 0& A\end{array}\right]\mathrm{s}\mathrm{i}\mathrm{n}\omega t$ is applied on the top surface of the plate with the electrically and magnetically open.

Eq. (11) can be rewritten as:

where $\mathbf{P}={\left[\begin{array}{lllllllllllllll}0& 0& 0& 0& 0& 0& 0& 0& A& 0& 0& 0& 0& 0& 0\mathrm{}\mathrm{}\mathrm{}\mathrm{}0\end{array}\right]}^T$.

If the piezoelectric parameter $C^l\left(i,j\right)$ is design variable, applying a partial differential on Eq. (25) with respect to $C^l\left(i,j\right)$, we have:

4. Numerical example

The material parameters of the functionally graded magneto-electro-elastic plate are given in Appendix. Thickness of the plate is $h=$ 0.05 m, semi-length of the plate $a=\mathrm{}$0.5 m.

In the present study, the following dimensionless parameters are employed:

where $C_{66}=\mathrm{}$10⁹ Pa is the elastic constant, ${\rho }^0=$ 1 kg/m³ is the density constant of plate. $e_s=\mathrm{}$1 C/m², $g_s=\mathrm{}$10^-10 As/Vm, $q_s=\mathrm{}$1 Vs/m², ${\mu }_s=\mathrm{}$10^-6 Vs/Am², For the mechanical loads, $q_0=\mathrm{}$1 N/m², and for the electrode excitation, $q_0=e_s{p}_0/h$, $p_0$ is a constant expressing the value of the electrostatic potential, and for the magnetic pole excitation, $q_0=e_s{p}_0/h$, $p_0$ is a constant expressing the value of the static magnetic potential.

A normal dimensionless harmonic mechanical excitation ${\stackrel{-}{\mathbf{F}}}_{}^T=\left\{\mathrm{0,0},\mathrm{0,0},\mathrm{0,0},\mathrm{0,0},1\right\}\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$ is applied on the top surface of plate.

We have studied the sensitivity of dynamic response of the FGM magneto-electro-elastic plate to its elastic parameters under the different frequency excitations

Notes: all the dynamic responses of the plate denote these of the middle surface of the plate. Fig. 2 illustrates that sensitivity of the dimensionless deflection responses of the plate to elastic parameter $C^l\left(i,j\right)$ under the different frequency excitations for $\lambda =\left(b/a\right)=\text{1}$. It can be found from Fig. 2 that the elastic parameters are most sensitive to the dimensionless deflection responses of the FG magneto-electro-elastic plate under the excitation of the dimensionless frequency 0.1357. From Fig. 2, it can be found that $C^l\left(\mathrm{4,4}\right)$ and $C^l\left(\mathrm{5,5}\right)$ have almost the same sensitivity, and they have the largest negative sensitivity of the dimensionless deflection response of the FG magneto-electro-elastic plate under the excitation of the dimensionless frequency 0.1357. $C^l\left(\mathrm{1,1}\right)$ and $C^l\left(\mathrm{2,2}\right)$ have nearly the same sensitivity. $C^l\left(\mathrm{1,3}\right)$ and $C^l\left(\mathrm{2,3}\right)$ have nearly the same sensitivity. Comparing the nine illustrations in Fig. 2, we found that $C^l\left(\mathrm{1,2}\right)$ has the largest positive sensitivity of the dimensionless deflection response of the FG magneto-electro-elastic plate under the excitation of the dimensionless frequency 0.1357. The negative sensitivity means that the deflection response of the plate will decrease when elastic parameters increase, the positive sensitivity is the opposite effect. It can be found from Fig. 2 that sensitivities of the dimensionless deflection response to the elastic parameters have small peaks when the dimensionless excitation frequency is 0.497. From the Fig. 2, it can be found that sensitivity of the dimensionless deflection response with respect to the elastic parameter $C^l\left(\mathrm{6,6}\right)$ is so small that can be neglected.

Fig. 2Sensitivity of the dimensionless deflection response of the plate to elastic parameter Cli,j under the different frequency excitations (λ=b/a=1)

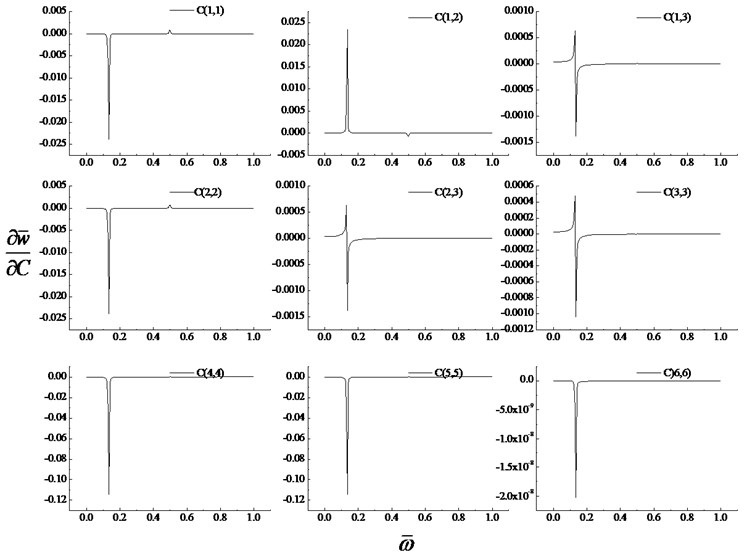
Fig. 3 shows the sensitivity of the dimensionless electric potential response of the plate to elastic parameter $C^l\left(i,j\right)$ under the different frequency excitations for $\lambda =\left(b/a\right)=\text{1}$. From Fig. 3, it can be seen that the elastic parameter $C^l\left(i,j\right)$ is especially sensitive to the dimensionless electric potential response of the plate, when the dimensionless excitation frequencies are 0.1357 and 0.497. $C^l\left(\mathrm{4,4}\right)$ and $C^l\left(\mathrm{5,5}\right)$ have almost the same sensitivity of the dimensionless electric potential response. $C^l\left(\mathrm{1,1}\right)$ and $C^l\left(\mathrm{2,2}\right)$ have almost the same sensitivity of the dimensionless electric potential response. $C^l\left(\mathrm{1,3}\right)$ and $C^l\left(\mathrm{2,3}\right)$ have almost the same sensitivity of the dimensionless electric potential response. The sensitive curves of $C^l\left(\mathrm{1,3}\right)$, $C^l\left(\mathrm{2,3}\right)$ and $C^l\left(\mathrm{3,3}\right)$ have the similar tendency. Among all the elastic parameters $C^l\left(\mathrm{4,4}\right)$ and $C^l\left(\mathrm{5,5}\right)$ have the maximum negative sensitivity of the dimensionless electric potential response of the plate when the dimensionless excitation frequency is 0.1357, and $C^l\left(\mathrm{1,2}\right)$ has the maximum positive sensitivity of the dimensionless electric potential response of the plate when the dimensionless excitation frequency is 0.1357. $C^l\left(\mathrm{1,1}\right)$ and $C^l\left(\mathrm{2,2}\right)$ have the maximum positive sensitive value of the dimensionless electric potential response of the plate when the dimensionless excitation frequency is 0.497, and $C^l\left(\mathrm{1,2}\right)$ has the maximum positive sensitive value of the dimensionless electric potential response of the plate when the dimensionless excitation frequency is 0.497. $C^l\left(\mathrm{4,4}\right)\text{,}$$C^l\left(\mathrm{5,5}\right)$ and $C^l\left(\mathrm{6,6}\right)$ are insensitive to the electric potential response when the dimensionless excitation frequency is 0.497. From the Fig. 2, it can be found that sensitivity of the dimensionless electric potential response with respect to the elastic parameter $C^l\left(\mathrm{6,6}\right)$ is so small that can be neglected.

Fig. 3Sensitivity of the dimensionless electric potential response of the plate to the elastic parameter Cli,j under the different frequency excitations (λ=b/a=1)

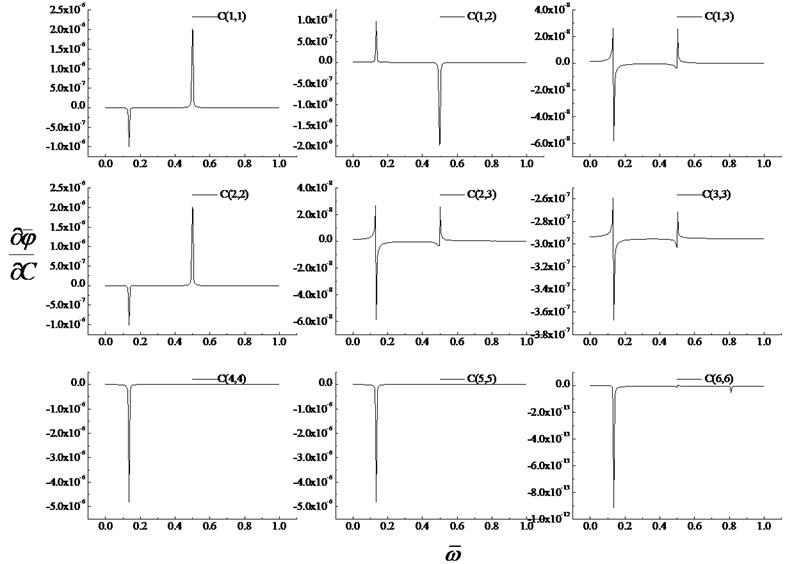
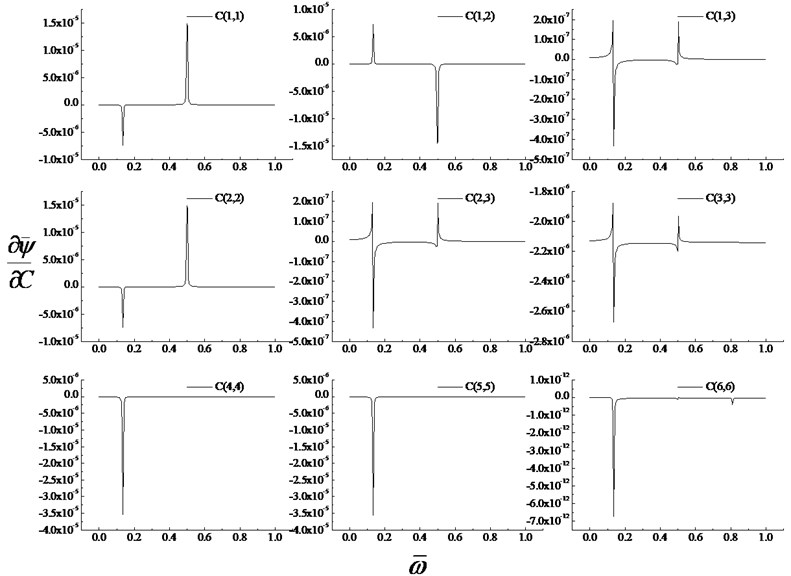
Fig. 4 shows that sensitivity of the dimensionless magnetic potential response of the plate to elastic parameter $C^l\left(i,j\right)$ under the different frequency excitation ($\lambda =\left(b/a\right)=\text{1}$). It can be seen from Fig. 4 that the sensitive curves of the dimensionless magnetic potential response have the same tendency as that of the dimensionless electric potential response. However, elastic parameters are more sensitive to the dimensionless magnetic potential response than to the dimensionless electric potential response.

5. Conclusions

The following conclusions can be obtained from the numerical example.

1) The elastic parameters $C^l\left(i,j\right)$ are especially sensitive to electric and magnetic potential responses of plate when the dimensionless excitation frequencies are 0.1357 and 0.497.

2) The elastic parameters $C^l\left(i,j\right)$ are more sensitive to the dimensionless deflect response of the excitation of the dimensionless frequency 0.1375 than that of the excitation of the dimensionless frequency 0.497.

3) Compared with other elastic parameters, $C^l\left(\mathrm{6,6}\right)$ is insensitive to all the dynamic response of the plate.

Fig. 4Sensitivity of the dimensionless magnetic potential response of the plate to elastic parameter Cli,j under the different frequency excitation (λ=b/a=1)

Analysis of the sensitivity for inverse techniques, optimization design and vibration control is a very meaningful. For the purpose of avoiding or reducing the ill-posed problems in inverse techniques, when the output such as the electric potentials and the magnetic potentials are measured by experiments, the excitation of a certain frequency which can obtain the most sensitivity must be acted on the plate. For the numerical example in the paper, we must apply the excitation with the dimensionless frequency 0.1357 on the plate, otherwise, Inverse technique can lead to serious ill-posed problems. Because $C^l\left(\mathrm{6,6}\right)$ is insensitive to all the dynamic response of the plate, an inverse problem of $C^l\left(\mathrm{6,6}\right)$ identification will be ill-posed.