A deep learning method using SDA combined with dropout for bearing fault diagnosis

Zhao, Wanlin; Lu, Chen; Ma, Jian; Wang, Zili

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

A deep learning method using SDA combined with dropout for bearing fault diagnosis

Wanlin Zhao¹

Chen Lu²

Jian Ma³

Zili Wang⁴

^{1, 2, 3, 4}School of Reliability and Systems Engineering, Beihang University, Beijing 100191, China

^{1, 2, 3, 4}Science and Technology on Reliability and Environmental Engineering Laboratory, Beijing 100191, China

Corresponding Author:

Wanlin Zhao

Cite the article Download PDF

Downloads 1306

Abstract

The fault diagnosis of a rolling bearing is at present very important to ensure the steadiness of rotating machinery. According to the non-stationary and non-liner characteristics of bearing vibration signals, a large number of approaches for feature extraction and fault classification have been developed. An effective unsupervised self-learning method is proposed to achieve the complicated fault diagnosis of rolling bearing in this paper, which uses stacked denoising autoencoder (SDA) to learn useful feature representations and improve fault pattern classification robustness by corrupting the input data, meanwhile employs “dropout” to prevent the overfitting of hidden units. Finally the high-level feature representations extracted are set as the inputs of softmax classifier to achieve fault classification. Experiments indicate that the deep learning method of SDA combined with dropout has an advantage in fault diagnosis of bearing, and can be applied widely in future.

1. Introduction

As one of the most common components, rolling bearings find widespread industrial applications and their failures cause malfunctions and may even lead to catastrophic failures of the machinery [1]. In view of the seriousness of this problem, fault diagnosis has been required to meeting customer demands, along with vibration signals generated by faults in bearing have been widely studied. Fault diagnosis can be regarded as a problem concerning pattern identification which mainly includes two important procedures: feature extraction and pattern classification [2]. It is well known that the extracted fault features have a great impact to the accuracy of the diagnosis results, and the vibration characteristic of rotating machinery is altered when a bearing has failed. For this reason, many feature extraction methods have been proposed to acquire more fault information from vibration signals and improve the accuracy of the diagnosis work, such as continuous wavelet transform, empirical mode decomposition (EMD), generalized Hilbert transform (HT), etc. The Hilbert-Huang transform (HHT) and EMD technique developed by Huang et al. has been used as an effective signal processing technique for machinery diagnostics [3]. However, it seems that information loss was induced by extracting time-frequency features manually, and many traditional learning algorithms were incapable of extracting and organizing the discriminative information from the data. Therefore unsupervised feature self-learning is proposed, which focuses on the unartificial and self-adaptive feature extraction.

In recent years, much attention is focused on the unsupervised learning which has been widely applied to solve the problems about computer vision, audio classification and NLP (Natural Language Processing), and the results show that the accuracy of the features learned with unsupervised learning algorithm is superior to others. Deep learning first proposed by Hinton et al. to establish a neural network to imitate the human brain learning process is a typical theory of unsupervised learning [4]. Researches show that deep learning has good results in terms of representing large-scale data and extracting features, for this reason, deep learning has an advantage over training data, especially for image and voice data which both have unconspicuous features needed manual design. However, it is noted that deep learning still has a rare application in the fault diagnosis of rotating machineries.

In this paper, a deep learning method called “autoencoder” is introduced to deal with the complicated conditions of bearings, which uses Stacked Denoising Autoencoder (SDA) to learn useful feature representations and improve fault pattern classification robustness by corrupting the input data and using denoising criterion [5]. SDA is a neutral network consisting of multiple layers of sparse autoencoder in which the outputs of each layer is wired to the inputs of the successive layer, in particular, a random “dropout” procedure is combined to SDA to achieve excellent results in this study. Dropout prevents overfitting of hidden units and provides a way of approximately combining exponentially many different neural network architectures efficiently [6]. As mentioned above, this paper used SDA method combined with “dropout” to achieve unsupervised self-learning to extract effective features of bearings and used softmax classifier to verify the validity of fault diagnosis.

This paper is structured as follows. Section 2 describes the unsupervised self-learning method of SDA, meanwhile the corresponding definitions and the application process of “dropout” is presented. In Section 3, we present our experimental results where we apply SDA method combined with dropout to extract features and softmax regression to classify faults. Sections 4 is a conclusion of the paper.

2. Methodology

In this section, the complete method based on deep learning for bearing fault diagnosis is presented, which consists of two parts: unsupervised feature self-learning based on SDA and dropout method, fine-tuning using softmax regression and fault pattern classification. The whole system and procedure are depicted in Fig. 1.

Fig. 1Fault diagnosis procedure of bearings based on SDA combined with dropout

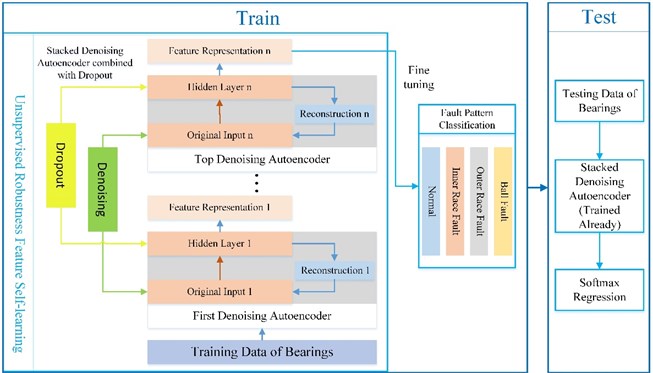
2.1. Model structure of SDA network combined with dropout

Here we introduce the basic parts of SDA network and detailed information of dropout technology.

1) Autoencoders.

Autoencoders aim to learn a compressed representation of data with minimum reconstruction loss. An autoencoder is a three-layer network including an encoder and a decoder. An encoder is referred to deterministic mapping $y = f_{θ} (x^{(i)}) = s i g m o i d (W x^{(i)} + b)$ that transforms an input vector $x$ into hidden representation $y$ , where $θ = {W, b}$ , $W$ is the weight matrix and $b$ is an offset vector [7]. On the contrary a decoder maps back the hidden representation $y$ to the reconstruction input $z$ via:

1

z = h_{W, b} (x^{(i)}) = g_{θ} (y) = s i g m o i d (W^{T} y + b^{T}) .

For a fixed training set ${(x^{(1)}, y^{(1)}), \dots, (x^{(m)}, y^{(m)})}$ of ‘ $m$ ’ training examples, the initial cost function is given by:

2

J (W, b) = [\frac{1}{m} \sum_{i = 1}^{m} J ((W, b); x^{(i)}; y^{(i)})] + \frac{λ}{2} \sum_{l = 1}^{n_{l} - 1} \sum_{i = 1}^{s_{l}} \sum_{j = 1}^{s_{l} + 1} {({W_{j i}}^{(l)})}^{2}

= [\frac{1}{m} \sum_{i = 1}^{m} \frac{1}{2} {‖h_{W, b} (x^{(i)}) - y^{(i)}‖}^{2}] + \frac{λ}{2} \sum_{l = 1}^{n_{l} - 1} \sum_{i = 1}^{s_{l}} \sum_{j = 1}^{s_{l} + 1} {({W_{j i}}^{(l)})}^{2},

where, the first term in $J (W, b)$ is an average sum-of-squares error term. The second term is a regularization term or weight decay term, which tends to decrease the magnitude of the weights and helps prevent over fitting. $λ$ is the weight decay parameter.

Considering the advantage of sparse input, the cost function is added the penalty:

3

J (W, b)_{s p a r s e} = J (W, b) + β \sum_{j = 1}^{s_{2}} K L (ρ ‖{\hat{ρ}}_{j}),

where $β$ controls the weight of the sparsity penalty term [8].

2) Denoising autoencoder.

Similar to a standard auto-encoder network, a denoising autoencoder is trained with the objective to learn a hidden representation that allows it to reconstruct its input. The difference is that the network is forced to reconstruct the original input from a corrupted version in order to force even very large hidden layers to extract intrinsic features. This corruption of the data is done by first corrupting the initial input $x$ to get a partially destroyed version $\tilde{x}$ by means of a stochastic mapping $\tilde{x} ~ q_{D} (\tilde{x} |x)$ . The standard approach used in this work is to apply masking noises to the data by setting a random fraction of the elements of $x$ to zero. Corrupted input $\tilde{x}$ is then mapped, as with the basic autoencoder, to a hidden representation $y = f_{θ} (\tilde{x}) = s i g m o i d (W \tilde{x} + b)$ from which we reconstruct a $z = g_{θ'} (y)$ . As before the parameters are trained to minimize the average reconstruction error $L_{Η} (x, z) = Η (Β_{x} ‖Β_{z})$ over a training set to have $z$ as close as possible to the uncorrupted input $x$ .

3) Stacked denoising autoencoder network.

In order to build a deep architecture, denoising autoencoders stack one on top of another, that’s stacked denoising autoencoder in this paper. A SDA is a neural network consisting of multiple layers of denoising autoencoders in which the outputs of each layer is wired to the inputs of the successive layer [9]. After the first autoencoder has been trained, the second is trained to encoder and reconstruct the hidden representation of the first one in a similar fashion. Finishing the training of all denoising autoencoders in this manner, a feed-forward network is constructed by connecting the first to the top autoencoder.

4) Dropout technology.

“Dropout” is a technique that aims to discourage brittle co-adaptions of hidden unit feature detectors [10]. The term “dropout” refers to dropping out some units in a neural network. By dropping an unit out, we mean temporarily removing it from the network, along with all its incoming and outgoing connections. The choice of which units to drop is random. In the simplest case, each unit is retained with a fixed probability $p$ independent of other units, where $p$ can be chosen using a validation set or can simply be set at 0.5 [11]. Dropping out is done independently for each hidden unit and for each training case.

Finally, connecting single denoising autoencoders trained above in turn, and adding a layer of softmax classifier, we can build an integrated SDA model, Fig. 2 presents the structure of the SDA model which has two hidden layers.

Fig. 2Structure of the SDA model

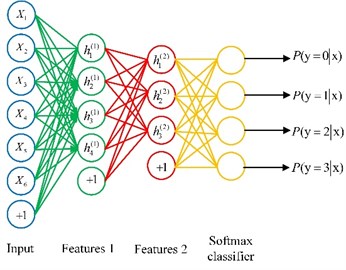
2.2. Unsupervised feature self-learning procedure

The procedure of unsupervised robustness feature self-learning is divided into two steps, the step 1 is single denoising autoencoder training [12]:

1) Pre-training of the initial data based on stochastic mapping: considering the robustness of fault diagnosis, the new input corrupted $\tilde{x}$ can be acquired using the stochastic process $q_{D}$ .

2) Encoder and decoder process of denoising autoencoder combined with dropout: randomly dropping out hidden units with a fixed probability. Then the encoder maps an input to its hidden representation $h_{i}$ using the non-linear mapping function. The decoder seeks to reconstruct the input $x_{i}$ from its hidden representation.

3) Minimizing the reconstruction error.

The step 2 is unrolling of all layers of SDA as a single model of feedforward neural network. High-level feature representation and optimized weights can be acquired when unsupervised robustness feature self-learning has been finished.

2.3. Fine-tuning based on softmax regression and fault pattern classification

Softmax regression is derived from logistic regression, which is more suitable for multi-classification. Feature vector acquired from SDA self-learning can be the input vector of softmax algorithm to realize the classification of multiple fault patterns. This method uses data labeled with fault patterns to train, minimization cost function to calculate the probability of each classification results, and global parameter tuning method to optimize the whole deep learning classifier, which can be tested using test data, and then the fault pattern of input data can be defined by the maximum probability label. The detailed procedure of softmax regression and fine-tuning is presented in the UFLDL course from Stanford.

3. Case study

Taking an example of data obtained from the Bearing Data Center of Case Western Reserve University, we present the implementation method of SDA combined with dropout for bearing fault diagnosis in this section.

3.1. Experimental bearing test-rig configuration

The bearing test-rig as shown in Fig. 3, consists of drive end (DE) and fan end (FE) bearings. Vibration data was collected using accelerometers, which were attached to the housing with magnetic bases, and accelerometers were placed at the 12 o’clock position at both the drive and fan end of the motor housing. Digital data was collected at 12,000 samples per second.

In this study, the DE bearing was chosen as object, and its detailed information is also presented in Fig. 3 and Table 1.

Fig. 3Bearing test-rig for experiment

Table 1Detailed information of the DE bearing

Bearing designation	Deep groove ball bearing	6205-2RS JEM SKF
Siai (inch)	Inside diameter	0.9843
	Outside diameter	2.0472
	Thickness	0.5906
	Ball diameter	0.3126
	Pitch diameter	1.537
Defect frequencies (Hz)	Normal	0
	Inner race fault	5.4152
	Outer race fault	3.5848
	Ball fault	4.7135

3.2. Experimental parameters setup

In this experiment, 98, 106, 119, 131 data were selected respectively as normal, inner race, outer race and ball fault data to verify the feasibility of the method.

Two denoising autoencoders were chosen to establish the unsupervised self-learning network in this study, that’s this neural network had two hidden layers, the first hidden layer had 50 nodes and the second had 25. According to the number of fault pattern needing classify, the node number of output layer was set 4. Learning from the theory of image recognition and comparing with others, the number of input nodes was selected for 16×16, which can contains sufficient data information and can ensure the computational efficiency. In addition, we injected noises to input data to reinforce the robustness of fault diagnosis, and applied dropout to hidden layers to prevent overfitting as described above. The parameters of the SDA combined with dropout model are listed in Table 2.

Table 2Parameters of the SDA combined with dropout model

Number of neurons	Input layer 1	Hidden layer 1	Input layer 2	Hidden layer 2	Output layer
Number of neurons	16×16	50	50	25	4
Denoising proportion	0.3		0.25
Dropout proportion		0.1		0
Learning parameters	Data interval		Learning rate
Learning parameters	2		1

3.3. Analysis of fault diagnosis results

Given all parameters as mentioned in Table 2, feature representation was extracted by training the unsupervised self-learning network, and it also was input to the softmax regression model to achieve the fault diagnosis of bearing. To represent the results of fault diagnosis better, we compared the results of fault pattern classification with real data, and calculated the proportion of the number classified correctly and the total number, that was the classification accuracy. The experimental results of the object selected above was present in Table 3.

Table 3Fault classification accuracy

Fault pattern	Normal	Inner race fault	Outer race fault	Ball fault	Total
Test data volume	60456	15217	15144	15271	106088
Classification error number	0	40	14	13	67
Classification accuracy	100 %	99.74 %	99.9076 %	99.9149 %	99.9368 %

From Table 3, we can see that the experiment had achieved a high classification accuracy, and it demonstrated the unsupervised robustness self-learning procedure based on the DE bearing can extract effective feature representation and then achieve good performance of fault pattern classification.

4. Conclusions

An unsupervised self-learning method using stacked denoising autoencoder is introduced in this paper, which is injected noise to input data of each autoencoder for robust feature reconstruction and effective high-level feature extraction, in addition, dropout technology is applied to hidden layers to discourage brittle co-adaptions. Followed by the top softmax regression classifier and fine-tuning, the model provides a way to improve the fault pattern classification accuracy of rolling bearings. Combined with the experiment, the effectiveness and feasibility of this method in the application of fault diagnosis is demonstrated. Future works are expected to focus on the application of the method to other object fault diagnosis and it might be interesting to compare stacked denoising autoencoder with other deep learning methods for training neural network.

References

Ben Ali J., Fnaiech N., Saidi L., et al. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Applied Acoustics, Vol. 89, 2015, p. 16-27.

Search CrossRef
Jiang H., Chen J., Dong G., et al. Study on Hankel matrix-based SVD and its application in rolling element bearing fault diagnosis. Mechanical Systems and Signal Processing, Vols. 52-53, 2015, p. 338-359.

Search CrossRef
Siegel D., Al-Atat H., Shauche V., et al. Novel method for rolling element bearing health assessment – a tachometer-less synchronously averaged envelope feature extraction technique. Mechanical Systems and Signal Processing, Vol. 29, 2012, p. 362-376.

Search CrossRef
Hinton G. E., Salakhutdinov R. R. Reducing the dimensionality of data with neural networks. Science, Vol. 313, Issue 5786, 2006, p. 504-507.

Search CrossRef
Vincent P., Larochelle H., Lajoie I., et al. Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion. Journal of Machine Learning Research, Vol. 11, 2010, p. 3371-3408.

Search CrossRef
Srivastava N. Improving Neural Networks with Dropout. Master’s thesis, University of Toronto, 2013.

Search CrossRef
Gehring J., Miao Y., Metze F., et al. Extracting deep bottleneck features using stacked auto-encoders. IEEE International Conference on Acoustics, Speech and Signal Processing, 2013, p. 3377-3381.

Search CrossRef
Verma N. K., Gupta V. K., Sharma M., et al. Intelligent condition based monitoring of rotating machines using sparse auto-encoders. IEEE Conference on Prognostics and Health Management, 2013, p. 1-7.

Search CrossRef
Qi Y., Wang Y., Zheng X., et al. Robust feature learning by stacked autoencoder with maximum correntropy criterion. IEEE International Conference on Acoustics, Speech and Signal Processing, 2014, p. 6716-6720.

Search CrossRef
Srivastava N., Hinton G., Krizhevsky A., et al. Dropout: a simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, Vol. 15, 2014, p. 1929-1958.

Search CrossRef
Dahl G. E., Sainath T. N., Hinton G. E. Improving deep neural networks for LVCSR using rectified linear units and dropout. IEEE International Conference on Acoustics, Speech and Signal Processing, 2013, p. 8610-8613.

Search CrossRef
Budiman A., Fanany M. I., Basaruddin C. Stacked denoising autoencoder for feature representation learning in pose-based action recognition. IEEE 3rd Global Conference on Consumer Electronics, 2014, p. 684-688.

Search CrossRef

About this article

Received

Accepted

28 July 2015

Published

18 September 2015

SUBJECTS

Fault diagnosis based on vibration signal analysis

Keywords

stacked denoising autoencoder

deep learning

dropout

bearing

fault diagnosis

Acknowledgements

This study is supported by the National Natural Science Foundation of China (Grant Nos. 61074083, 50705005, and 51105019) and by the Technology Foundation Program of National Defense (Grant No. Z132013B002).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.