Application of wave based method for predicting the response of coupled vibro-acoustic system with unconstrained damping layer

Xia, Xiaojun; Xu, Zhongming; Lai, Shiyang; Zhang, Zhifei; He, Yansong

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

Application of wave based method for predicting the response of coupled vibro-acoustic system with unconstrained damping layer

Xiaojun Xia¹

Zhongming Xu²

Shiyang Lai³

Zhifei Zhang⁴

Yansong He⁵

^{1, 2}State Key Laboratory of Mechanical Transmission, Chongqing, China

^{3, 4, 5, 2}College of Automotive Engineering of Chongqing University, Chongqing, China

Corresponding Author:

Zhongming Xu

Cite the article Download PDF

Downloads 1166

Abstract

The Wave Based Method (WBM) is a deterministic prediction method that is computational efficiency as compared to other deterministic prediction techniques in mid-frequency problems. This paper discusses the application of WBM for predicting the dynamic displacement of plate with an unconstrained damping layer based on Kirchhoff theory. Further, the prediction of acoustic response of the coupled vibro-acoustic system with unconstrained damping is realized on the use of WBM. A numerical example is introduced, and the comparison of numerical result obtained by WBM and FEM is acquired. It is seen that the WBM is applicable for vibro-acoustic system with unconstrained damping and is expected to yield faster and more accurate predictions. The limitation of the method caused by simplify hypothesis is described in combination with modelling ways and numerical results.

1. Introduction

The element based methods such as FEM and BEM are limited for low-frequency problems because of its high computational cost and increasing error as frequency increasing [1]. While the statistical methods like SEA [2] are merely suit for high frequency problems. So an efficient numerical technique for simulating and predicting the mid-frequency problems is desired. Wave based method (WBM) as a deterministic method this paper focuses on is a better choice. At present, WBM has shown its high accuracy and low compute cost in contrast with existing deterministic method when predicting the vibro-acoustic response in mid-frequency [3]. Meanwhile, as one of the most common and convenient methods for vibration and noise reduction, adding an unconstrained damping layer on plate like structure is wildly adopted in engineering. The analytic method to analysis the dynamic displacement of composite is proposed based on the Kirchhoff theory [4, 5].The application of such efficient numerical predictive technique for vibro-acoustic system with unconstrained damping is indispensable and valuable.

This paper starts with the description of dynamic vibration of a plate with unconstrained damping based on the Kirchhoff theory and the description of government equations of coupled vibro-acoustic system. The following section describes the basic principle of WBM for coupled vibro-acoustic system with unconstrained damping layer. A numerical example demonstrates the validity and the efficiency of the presented method finally.

2. Basic methodology of coupled vibro-acoustic system

2.1. Vibration of plate with an unconstrained damping layer

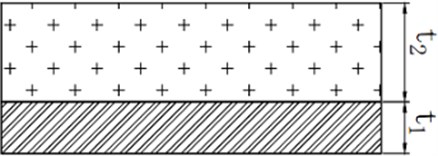
Fig. 1 shows the section of composite plate. $t_{1}$ , $t_{2}$ is the thickness of steel layer and damping layer respectively. The dynamic displacement government equation based on Kirchhoff theory is:

1

B^{*} \nabla^{4} w_{t} (x^{s}, y^{s}) + \tilde{m} \frac{\partial^{2} w^{t} (x^{s}, y^{s})}{\partial t^{2}} = Q_{t} .

With $\tilde{m} = ρ_{1} t_{1} + ρ_{2} t_{2}$ the unit mass of plate, $Q_{t}$ the external load. $B^{*}$ represents the complex bending stiffness under the Kirchhoff hypothesis, which defined as:

2

B^{*} = \frac{E_{1}^{*} t_{1}^{3}}{12 (1 - u_{1}^{2})} + \frac{E_{2}^{*}}{1 - u_{2}^{2}} (\frac{t_{2}^{3}}{12} + t_{2} + t_{21}^{2}),

where $t_{21} = t_{1} + t_{2} / 2$ , $E_{1}^{*} = E_{1} (1 + j η_{1})$ , $E_{2}^{*} = E_{2} (1 + j η_{2})$ , $e_{2} = E_{2} / E_{1}$ , $h_{2} = t_{2} / t_{1}$ . $E_{i}$ , $η_{i}$ , $i = 1, 2$ is elasticity modulus and material loss factor of each layer correspondingly.

Fig. 1Structure of a plate with unconstrained damping

2.2. Government equation of vibro-acoustic system

For a steady-state harmonic excitation $Q_{t} = Q e^{j ω t}$ , displacement and the excitation can be written as $w_{z} (x^{s}, y^{s}) e^{j ω t}$ , subsequently, the steady government equation of the composite plate of vibro-acoustic system is redefined as:

3

{\nabla^{4} w}_{z} (x^{s}, y^{s}) - {(k_{b}^{*})}^{4} w_{z} (x^{s}, y^{s}) = \frac{Q}{B^{*}} δ (x_{F}^{s}, y_{F}^{s}) + \frac{p (x^{a s}, y^{a s}, z^{a s})}{B^{*}},

where $\nabla^{4} = \partial^{4} / {\partial x}^{4} + \partial^{4} / {\partial x^{2} \partial y}^{2} + \partial^{4} / {\partial y}^{4},$ $k_{b}^{*} = \sqrt[4]{\tilde{m} ω^{2} / B^{*}}$ is the plate bending wave number, $(x_{F}^{s}, y_{F}^{s})$ is the location of external load. $p (x^{a s}, y^{a s}, z^{a s}) / B^{*}$ describes the acoustic load acting on the coupled interface $(x^{a s}, y^{a s}, z^{a s})$ .

The Helmholtz equation of the steady pressure of associated cavity is:

4

\nabla^{2} p (r) + k^{2} p (r) = 0,

with $\nabla^{2} ＝ \partial^{2} / {\partial x}^{2} + \partial^{2} / {\partial y}^{2} + \partial^{2} / {\partial z}^{2}$ the Laplace operator, $r$ the coordinate in cavity, $k$ the acoustic wavenumbers.

3. Wave based method

The WBM belongs to the category of indirect Trefftz methods. As the Trefftz principle, the field variables within convex domain are approximated by an expansion of basis functions, which exactly satisfy the governing dynamic equations. The errors on the boundary is forced to zero through weighted residual formulation, then the contribution factor of each basis function are determined. Subsequently, the displacement and acoustic response of vibro-acoustic system are obtained.

3.1. Field variable expansion

The variables, the out of plane displacement $w_{z}$ of composite plate and the pressure $p$ of cavity, are approximated by the following field variable expansion:

5

w_{z} \approx \sum_{i = 1}^{n_{s}} w_{s i} ψ_{s i} + \sum_{i = 1}^{n_{a}} p_{a i} w_{s i} + {\hat{w}}_{F} = [ψ_{s}] \{w_{s}\} + [p_{a}] \{φ_{a s}\} + {\hat{w}}_{F},

6

p \approx \sum_{i = 1}^{n_{a}} p_{a i} ϕ_{a_{i}} = [ϕ_{a}] \{p_{a}\},

With $ψ_{s}$ , $ϕ_{a}$ the wave functions vectors, $w_{s}$ , $p_{a}$ the corresponding contribution factors vectors of displacement and pressure respectively. And the wave function defined as:

7

ψ_{s i} = e^{- j (k_{x s i} x + k_{y s i} y)}, ϕ_{a i} = e^{- j (k_{x a i} x + k_{y a i} y + k_{z a i} z)} .

With ${(k_{x s i}^{2} + k_{y s i}^{2})}^{2} = {k_{b}^{*}}^{4}$ , and $k_{x a i}^{2} + k_{y a i}^{2} + k_{z a i}^{2} = k^{2}$ .

${\hat{w}}_{F}$ serves as the particular solution for external point force excitation:

8

{\hat{w}}_{F} = - \frac{j F}{8 {k_{b}^{*}}^{2} B^{*}} [H_{0}^{(2)} (k_{b}^{*} r_{F}) - H_{0}^{(2)} (- j k_{b}^{*} r_{F})],

where $r_{F}$ is the distance to the location of exciting point $(x_{F}, y_{F})$ .

$ϕ_{a s}$ is the pressure load results from the acoustic wave functions $ϕ_{a}$ , defined as:

9

φ_{a s} (x^{s}, y^{s}) = - \frac{j}{8 {k_{2}^{*}}^{2} B^{*}} \int_{Ω_{s}}^{} ϕ_{a} (x^{a s}, y^{a s}, z^{a s}) H_{0}^{(2)} (k_{b}^{*} r_{s}) d_{s}

+ \frac{j}{8 {k_{2}^{*}}^{2} B^{*}} \int_{Ω_{s}}^{} ϕ_{a} (x^{a s}, y^{a s}, z^{a s}) H_{0}^{(2)} (- j k_{b}^{*} r_{s}) d_{s} .

With $r_{s}$ the distance to $(x^{s}, y^{s})$ .

3.2. Coupled vibro-acoustic wave model

The wave functions of plate and acoustics satisfy the corresponding government equations. The boundary residual is enforced to zero through weighted formula, like the Galerkin weighting procedure used in FEM. This yields a matrix equation consisting of $n_{s} + n_{a}$ algebraic equations in the $n_{s} + n_{a}$ unknown wave function contribution factors:

10

[\begin{matrix} A_{a a} + C_{a a} & C_{a s} \\ C_{s a} & A_{s s} \end{matrix}] \{\begin{array}{l} p_{a} \\ w_{s} \end{array}\} = \{\begin{array}{l} f_{a} \\ f_{s} \end{array}\},

11

A_{a a} = \overset{}{\int_{Γ_{v}}} ϕ_{a}^{T} L_{v} (ϕ_{a}) d Γ,

12

C_{a a} = - \int_{Γ_{s}}^{} j ω ϕ_{a}^{T} ϕ_{a s} d Γ,

13

C_{a s} = - \int_{Γ_{s}}^{} j ω ϕ_{a}^{T} ψ_{s} d Γ,

14

C_{s a} = \int_{Γ_{w θ}}^{} L_{Q_{n}} [ψ_{s}^{T}] w_{a s} d Γ + \int_{Γ_{w θ}}^{} L_{m_{n}} [ψ_{s}^{T}] L_{θ_{n}} (w_{a s}) d Γ,

15

A_{s s} = \int_{Γ_{w θ}}^{} L_{Q_{n}} [ψ_{s}^{T}] [ψ_{s}] d Γ + \int_{Γ_{w θ}}^{} L_{m_{n}} [ψ_{s}^{T}] L_{θ_{n}} [ψ_{s}] d Γ,

16

f_{a} = \int_{Γ_{v}}^{} ϕ_{a}^{T} {\bar{v}}_{n} d Γ - \int_{Γ_{s}}^{} ϕ_{a}^{T} (j ω w_{F}) d Γ,

17

f_{s} = \int_{Γ_{w θ}}^{} L_{Q_{n}} [ψ_{s}^{T}] ({\bar{w}}_{z} - {\hat{w}}_{F}) d Γ + \int_{Γ_{w θ}}^{} L_{m_{n}} [ψ_{S}^{T}] ({\bar{θ}}_{n} - L_{θ_{n}} ({\hat{w}}_{F})) d Γ,

where $Γ_{v}$ , $Γ_{w θ}$ , $Γ_{s}$ is the acoustic boundary, plate boundary and coupled interface respectively. $L_{v}$ , $L_{Q_{n}}$ , $L_{θ_{n}}$ and $L_{m_{n}}$ is the differential operators for acoustic velocity, the normal rotation of plate, the bending moment of plate and the generalized shear force of plate. After solving the matrix equations, the obtained contributions $p_{a}$ and $w_{s}$ are substituted back to Eqs. (5) and (6) to acquire the variables $p$ and $w_{z}$ .

4. Numerical example

4.1. Problem description

In order to validate the described methodology and show its capabilities a numerical example is given. The considered geometry of coupled vibro-acoustic system is shown in Fig. 2. The parameters of composite plate are presented in Table 1. A unit point force is applied at (0.2 m, 0.2 m, 0.5 m) and a reference point R(0.4 m, 0.3 m, 0.5 m) in cavity is selected. WBM model is built in MATLAB R2015a, and the FEM model is built with MSC/Nastran.

Fig. 2Problem geometry

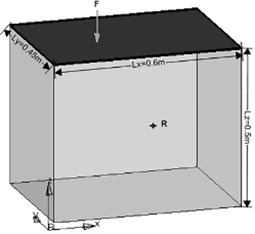
Table 1Parameters of composite plate

Material	Thickness (mm)	Density (kg/m³)	Elasticity modulus (pa)	Poisson coefficient	Loss factor
Aluminum	1.0	2700	7.2e10	0.33	0
Damper	2.0	1300	1e8	0.45	0.8

4.2. Result

As we know, the accuracy of FEM is improving with decreasing the size of element to some degree, which, however, increases the computational cost and limits its capacity for higher frequency problems. To illustrate the influence of element size, coarse FE model with 20 element size and fine FE model with 5 element size are built. Fig. 3 plots the acoustic response of reference point calculated by FE and WBM at 50-500 Hz. The comparison shows that the result obtained by WBM agrees with the result obtained by fine FE model better than the coarse one. The influence of damping layer is revealed through the comparison with the undamping model, and the average amplitude of acoustic response is reduced dramatically compared with the damping model.

Fig. 4 shows the displacement contour of composite plate calculated by WBM with 262 wave functions and FEM with fine mesh at 100 Hz. It is seen that the displacement is zero at the clamped edge that satisfy the boundary condition. And the result obtained by WBM can agree with the result obtained by fine FE model basically.

The error generated by this methodology is mainly caused by: (1) WBM makes use of the Kirchhoff plate theory to model plate bending problems, whereas the FEM in MSC/Nastran is based on the Reissner-Mindlin theory that considers the rotatory inertia and shear deformation. (2) The composite plate is treated as a single plate in WBM, while the damping layer is built by solid element in FEM. So the thicker damping layer, the influence more serious, which restricts that this method is applied only to the thin plate that according with the Kirchhoff hypothesis.

Fig. 3The acoustic response curves of system: a) with and b) without unconstrained damping

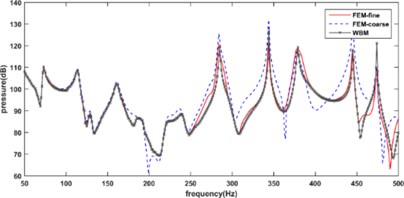
a)

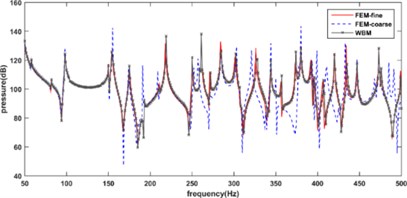
b)

In contrast with the FEM, the advantages of the application using WBM for predicting coupled system with unconstrained damping is obvious and significant.it has a higher convergence rate and convenient modeling produce. Table 2 shows convergence of WBM and FEM. The comparison demonstrates that WBM can get the acceptable result with much less computational cost than FEM especially for mid-frequency problems.

Fig. 4Displacement contour of composite plate at 100 Hz: a) WBM and b) FEM

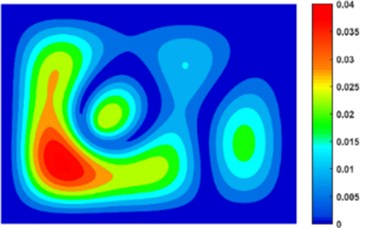
a)

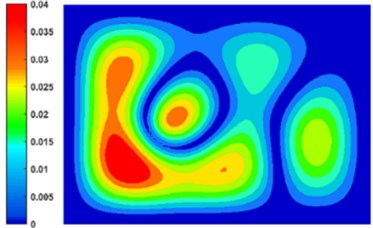
b)

Table 2The DOF and corresponding pressure amplitude of reference point at 60 Hz

WBM		FEM
Pressure (Pa)	Wave functions	Pressure (Pa)	Nodes
2.6053	132	2.7659	10925
2.5088	164	2.5543	20834
2.4368	198	2.4768	45758
2.4217	230	2.3784	148718
2.4217	258	2.3768	1134133

5. Conclusion and future work

This paper describes the method to predict vibration of plate with an unconstrained damping layer through the complex stiffness. Subsequently, the methodology for predicting the coupled vibro-acoustic system with unconstrained damping is presented. The last section gives a numerical example, which compares the result obtained by WBM to the results obtained by FEM with different sizes. In the example, the WBM shows a higher convergence rate and lower computational cost in contrast with FEM. The comparison validates the effectiveness of this method for predicting coupled vibro-acoustic system with unconstrained damping layer.

An interesting next step is to explore the availability for acoustic optimization based on this method. Furthermore, an experimental validation of the obtained numerical results is foreseen.

References

Hartmann F., Zotemantel R. The direct boundary element method in plate bending. International Journal for Numerical Methods in Engineering, Vol. 21, Issue 11, 1986, p. 2049-2069.

Search CrossRef
Lyon R., DeJong R. Theory and Application of Statistical Energy Analysis (2nd Edition). Butterworth Heinemann, 1995.

Search CrossRef
Desmet W. A Wave Based Prediction Technique for Coupled Vibro-Acoustic Analysis. Leuven, 1998.

Search CrossRef
Zheng Baizhe, Li Yahong, Zhu Yuxiang Theoretical and experimental research of the vibration characteristics of the damped plate composed of an elastic metal layer and an unconstrained viscoelastic layer. Engineering Mechanics, Vol. 8, Issue 3, 1991, p. 129-138.

Search CrossRef
Leissa A. Vibration of Plates. Acoustical Society of America, Woodbury, New York, 1993.

Search CrossRef
Vanmaele C., Vandepitte D. An efficient wave based prediction technique for plate bending vibrations. Computer Methods in Applied Mechanics and Engineering, Vol. 196, Issues 33-34, 2007, p. 3178-3189.

Search CrossRef
luymers B., et al. Trefftz-based methods for time-harmonic acoustics. Archives of Computational Methods in Engineering, Vol. 14, Issue 4, 2007, p. 343-381.

Search CrossRef
Vergote K., et al. An efficient wave based approach for the time-harmonic vibration analysis of 3D plate assemblies. Journal of Sound and Vibration, Vol. 332, Issue 8, 2013, p. 1930-1946.

Search CrossRef

About this article

Received

Accepted

21 August 2015

Published

18 September 2015

SUBJECTS

Mechanical vibrations and applications

Keywords

wave based method

vibro-acoustic

unconstrained damping

Kirchhoff theory

Acknowledgements

The research work of Xia Xiaojun is financed by Chongqing Graduate Student Research Innovation Project (CYB14036).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.