Bending vibration prediction of orthotropic plate with wave-based method

1. Introduction

With the improvement of material technology and increase of demand for structure performance, more and more composite materials like honeycomb panels and fibre reinforced polymers are adopted to lower weight of the products in aerospace and automotive industry. Among which, thin orthotropic plate is the typical structure used in such transport production, and the bending vibration behavior of this class structure is the key factor to influence NVH performance of product. Thus, the response of orthotropic plate has been talked about by analytical or semi-analytical methods [1-4]. With the requirement of lowering the cost of time and computation, the CAE techniques based on numerical method is indispensable for engineers to predict the deterministic bending vibration response of such composite structure, especially in design and optimization process.

Currently, the element based methods like Finite Element Method (FEM) [5] and Boundary Element Method (BEM) [6] are proverbially applied for vibration and acoustic prediction. They divide the problem domain into finite elements, in which the variables are approximated by a set of simple polynomial functions that is not exactly satisfy the physical governing equation and boundary conditions, which results interpolation error and pollution error [7]. For higher frequency problems, the element size need to be small enough to capture the property of short wavelength, which sharply increasing the computational cost and time. Therefore, the element based methods usually used in low frequency issues. On the other hand, the Statistical Energy Analysis (SEA) [8] divides the system into finite subsystem, and the dynamical response of system is calculated through the balance and exchange of different subsystems. However, such statistical method is merely available for higher frequency problems under the theoretical hypothesis that each subsystem has high modal density during concerning frequency range. In the frequency range between the low and high frequency, called mid-frequency, system contains long wavelength and short wavelength characteristic, so a high efficiency and high robustness numerical method is necessary for predicting the vibration feature of structure.

Over the recent years, a variety of techniques have been proposed to deal with the mid-frequency problems. And the first idea is extending the frequency range of present methods, such the Galerkin least-squares FEM [9], the quasi-stabilized FEM [10], Statistical energy analysis energy method [11], Energy-density field approach [12], Hybrid SE-FEM [13]. the other family of solution algorithms is based on Trefftz method [14] which describes the field variables with a combinations of basis functions that satisfy the governing equation. Such approaches include the ultra-weak variational method [15], the wave boundary element method [16], The variational theory of complex rays [17]. The Wave Based Method(WBM) which is addressed in this paper is belongs to this family of solutions.

In the end of 20 centuries, W. Desmet proposed a novel numerical technique for mid-frequency vibro-acoustic problems [18], its advantages of high accuracy and convergence is revealed. Then WBM is widely applied for prediction of sound and vibration areas. For example, vibration of thin and thick plate [19, 20], analysis of vibro-acoustic radiation problems [21], modelling of Poroelastic Materials [22]. In order to break through the application limitation that WBM is only convergence in convex domain, many extending techniques are present, like multi-level wave based technique [23], Hybrid FEM-WBM [24], Hybrid BEM-WBM [25]. Therefore, the extending of this techniques is significant for engineering application.

This study aims to propose a novel efficient numerical approach based on the theory of wave based method and the orthotropic plate. This paper is organized as follow. The vibration theory of orthotropic plate is reviewed in Section 2. The basic formulation of WBM for orthotropic plate is derived, and the particular solution of orthotropic plate resulted by concentrated force is obtained through Fourier transform in Section 3. The numerical examples are presented and the methodology is validated in Section 4. Finally, the conclusions are drawn in Section 5.

2. Vibration of orthotropic plate

For plate vibration analysis, there are two main theories: The Kirchhoff and the Resissner Mindlin theory. Kirchhoff theory assumes that the shear deformation of plate is zero, or that the normal of the middle plane remain normal during deformation. The Kirchhoff assumption remains valid as long as the bending wavelength is approximately six times larger than the plate thickness. In view of the objective is thin plate, Kirchhoff theory is adopted for describing the vibration feature of orthotropic plate. For a thin orthotropic plate, when $x$, $y$ axis parallel to the elastic principal direction, its transversal displacement $w$ is governed by the orthotropic Kirchhoff equation under external excitation $f\left(x,y,t\right)$ [1]:

where orthotropic plate parameters are given as:

with Young’s modulus $E_1$, $E_2$ and Poisson’s ratios ${\nu }_1$, ${\nu }_2$ in the directions of the coordinate axes $x$ and $y$ respectively, $G$ the shear modulus in $xy$ plane. $\rho$ the plate material density and $h$ the plate thickness.

For a time harmonic load $f\left(x,y,t\right)=F\left(x,y\right)e^{-i\omega t}$ with circular frequency $\omega$, the steady-state response of orthotropic plate changed as:

To solve the fourth-order equation and acquire the out-of-plate displacement $w$, two structural boundary conditions are required. The common boundary conditions at plate edges are defined as follow:

Dynamical boundary:

Mechanical boundary:

Mix boundary:

With $\stackrel{-}{w}$, $\stackrel{-}{\theta }$, $\stackrel{-}{M}$ and $\stackrel{-}{V}$ the boundary value for respectively, the displacement, the rotational displacement, the bending moment and the equivalent shear force. $L_{\theta }$, $L_M$, $L_V$ the differential operators for rotational displacement, bending moment, and the equivalent shear force. The corresponding variables in orthotropic material are defined as follow:

Rotational displacement:

Bending moment:

Equivalent shear force:

3. Wave based method

Wave based method that belongs to indirect Treffz method is a deterministic numerical technique, in which the field variables are expressed as a combination of set of wave functions that satisfy the governing equation exactly. On the use of weighted residual formulation, the boundary errors are enforced to zeros and the contribution factors of wave functions are determined. Subsequently, the approximation of out-of-plate displacement is obtained.

3.2. Particular solution

${\widehat{w}}_F\left(x,y\right)$ in Eq. (9), which is the particular solution of Eq. (2), denotes the dynamic response of infinite plate by external load. In this paper, a concentrated point force in consider. For a time harmonic point force in the $z$-direction at $\left(x_0,y_0\right)$, the load expressed as:

16

$f\left(x,y,t\right)=F{e}^{-i\omega t}\delta \left(x-x_0\right)\delta \left(y-y_0\right).$

So, the Eq. (2) changed as:

17

$D_{11}\frac{{\partial }^{4}w}{\partial x^4}+2\left(D_{12}+2D_{66}\right)\frac{{\partial }^{4}w}{\partial x^2\partial y^2}+D_{22}\frac{{\partial }^{4}w}{\partial y^4}-\rho h{\omega }^{2}w=F\delta \left(x-x_0\right)\delta \left(y-y_0\right).$

Transforming ${\widehat{w}}_F\left(x,y\right)$ into wavenumber domain $\left(k_x,k_y\right)$ by Fourier Transform, the displacement response is expressed as:

18

$\tilde{w}\left(k_x,k_y\right)={\iint }_{-\infty }^{\infty }w{\left(x,y\right)}_F{e}^{-i\left(k_{x}x+k_{y}y\right)}dxdy,$

19

$w_F\left(x,y\right)=\frac{1}{{\left(2\pi \right)}^2}{\iint }_{-\infty }^{\infty }{\tilde{w}\left(k_x,k_y\right)e}^{-i\left(k_{x}x+k_{y}y\right)}d{k}_{x}d{k}_y.$

So, the Eq. (17) is transformed in the same way and the integration variables are changed from $\left(k_x,k_y\right)$ to $\left(k,a\right)$ with $k_x=k\cos \left(a\right)\text{,}$$k_y=k\sin \left(a\right)\text{.}$ And the rectangular coordinate is transformed into cylindrical coordinate by $x=r\cos \left(\theta \right)$, $y=r\sin \left(\theta \right)$. Integrating Eq. (20) form $\theta -\pi /2$ to $\theta +3\pi /2$, yields the approximation of particular solution for an infinite orthotropic plate [26]:

20

$w_F\left(x,y\right)\approx \frac{iF}{{\left(2\pi \right)}^2}{\int }_{\theta -\frac{\pi }{2}}^{\theta +\frac{\pi }{2}}\frac{\exp \left(i{k}_f\left(a\right)r\mathrm{c}\mathrm{o}\mathrm{s}\left(a-\theta \right)\right)}{{4k}_f^2\left(a\right)G\left(a\right)}da,$

where:

21

$k_f\left(\alpha \right)={\left(\frac{{\omega }^2\rho h}{G\left(a\right)}\right)}^{1/4},$

22

$G\left(a\right)=D_{11}{\cos \left(a\right)}^4+2\left(D_{12}+{2D}_{66}\right){\mathrm{c}\mathrm{o}\mathrm{s}\left(a\right)}^2{\mathrm{s}\mathrm{i}\mathrm{n}\left(a\right)}^2+D_{22}{\mathrm{s}\mathrm{i}\mathrm{n}\left(a\right)}^4.$

To reveal the feature of particular solution for orthotropic plate, the displacement of a square Graphite–epoxy plate with size (0.2 m×0.2 m) that is excited by a unit force in the center is calculated with the proposed approach. The material parameters of plate including: fiber angle = 0, $E_{11}=$ 138 GPa, $E_{22}=$ 8.9 GPa, $G_{12}=$ 5.176 GPa, ${\nu }_{12}=$ 0.3, $\rho =$ 1600 kg/m³, $h=$ 0.005 m. The result shown in Fig. 1 is the real part and imaginary part of displacement of the orthotropic plate respectively. Comparing with isotropic plate, the propagation of wave is no longer axisymmetric but varies with the modulus of each principal direction.

Fig. 1Displacement response of an infinite orthotropic plate

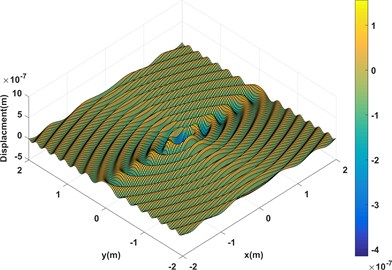
a) Real part

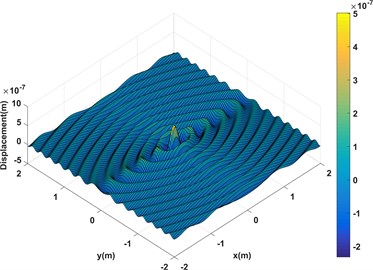
b) Imaginary part

4. Numerical validation and discussion

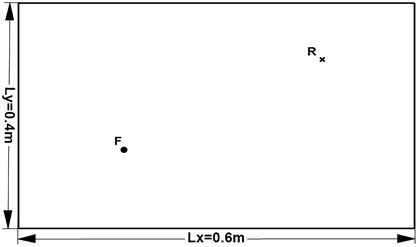
To validate the proposed methodology, a rectangular orthotropic plate is introduced. The problem geometry is depicted in Fig. 2 and is same for all the case. The plate is made of a unidirectional fibre reinforced polymer whose material parameters is presented in Table 1. The plate has a thickness of 0.001 m and a unit normal force is applied at $\left(x_q,y_q\right)=$(0.16 m, 0.14 m). A response point $R$ that is selected for surveying its frequency response located at (0.46 m, 0.3 m). The simply supported and clamped boundary condition will be considered. And there are two key points to be validated: the one is the accuracy which is illustrated in Section 4.1 and 4.2, another is the efficiency that is specified in Section 4.3.

WBM is implemented in MATLAB with truncation coefficient $T=$6. With the purpose of validation of WBM for predicting the bending vibration of orthotropic plate, WBM predictions are compared with those obtained by FEM. FEM is realized by MSC/Nastran2012 in this study. In order to ensure the accuracy of calculation, FE model is fine meshed with eight-node quadrilateral shell element and is consisted of degrees of freedom 45501. All FE models are solved by using the direct solution method.

Fig. 2Problem geometry

4.1. Simply supported plate

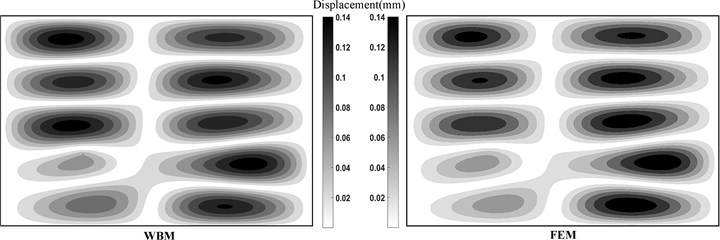
In this validation example, all the boundaries of orthotropic plate are simply supported. Fig. 3 shows the compared contour of displacement with both WBM and FEM at 200 Hz. The displacement response obtained by WBM is considerable agree with those obtained by FEM.

Fig. 3Displacement of orthotropic plate with simply supported boundary at 200 Hz

In consideration of four simply supported boundary, the doubly infinite series type of solution for such orthotropic plate is available [27]. So, the series solution is introduced to demonstrate the validity of WBM:

27

$w\approx \sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{D}_{mn}\sin \left(\frac{m\pi x}{L_x}\right)\sin \left(\frac{n\pi y}{L_y}\right),$

where:

28

$D_{mn}=\frac{4}{\alpha \beta {\pi }^4\left(D_{12}+2D_{66}\right)L_x{L}_y\left[{\left(\frac{m}{L_x}\right)}^4+2\gamma {\left(\frac{m}{L_x}\right)}^2{\left(\frac{n}{L_y}\right)}^2+{\left(\frac{n}{L_y}\right)}^4-\frac{\gamma }{{\pi }^4}\right]}\sin \left(\frac{m\pi x_q}{L_x}\right)\sin \left(\frac{n\pi y_q}{L_y}\right),$

with $\alpha =\sqrt[4]{D_{11}/D_{12}+2D_{66}}$, $\beta =\sqrt[4]{D_{22}/D_{12}+2D_{66}}$, $\gamma =\rho h{\omega }^2/D_{12}+2D_{66}$, $m$, $n$ is the wave number of half-sinusoid in $x$, $y$ direction separately, and $m=n=$ 50 in this study.

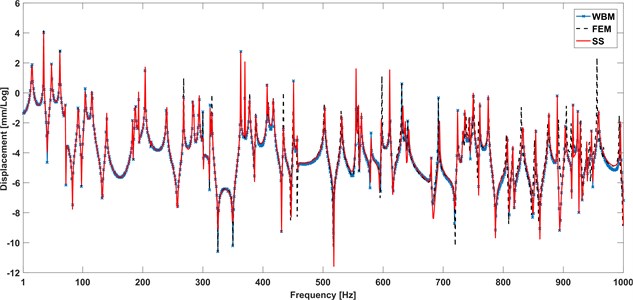
Fig. 6 shows the predictive displacement response of selected point $R$ within 1-1000 Hz. in order to reflect the nuance of three plot obtained by different approaches, the compared results are presented in the form of logarithm. Form the plots, the results by using the WBM based approach is in good agreement with the results calculated by FEM and series method, which verifies that WBM is applied to predict the bending vibration of orthotropic plate with simply supported edges.

Fig. 4Frequency response of response point R with simply supported boundary

4.2. Clamped plate

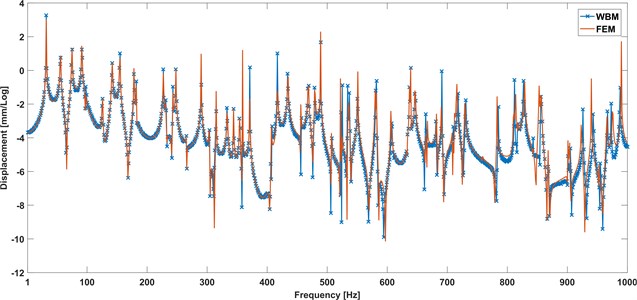
In this section, the example with all boundaries clamped is discussed. Similar to the Section 4.1, this section is to validate the accuracy of WBM for orthotropic plate with clamped boundary. The displacement contours at 150 Hz predicted by WBM and FEM are depicted in Fig. 5, in which we can see the predictions with WBM are fit well with the FEM analysis. Additionally, the logarithmic frequency responses of selected point $R$ in 1-1000 Hz shown in Fig. 6 similarly certifies that the proposed approach based on WBM is available for predicting the bending vibration of orthotropic plate precisely.

Fig. 5Displacement of orthotropic plate with clamped boundary at 150 Hz

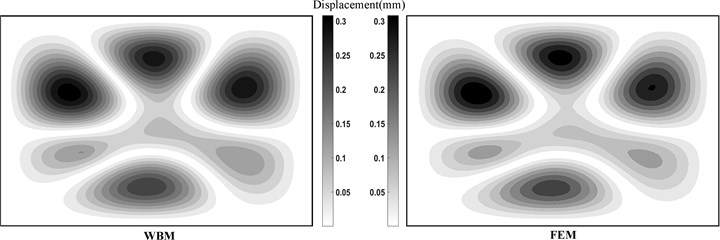
Fig. 6Frequency response of response point R with clamped boundary

4.3. Convergence

As mentioned above, the aim of numerical examples is to validate the method in both accuracy and efficiency. And the proposed approach based on WBM is validated that this method is precisely available for prediction of translational displacement of thin orthotropic plate. Then, the efficiency of WBM is illustrated in this section via the convergence analysis.

The accuracy of WBM and FEM are ensured by number of truncation parameters and by the number of element respectively. And the number of wave function in WBM and number of node in FEM is the decision of computational cost and corresponding computing precision. To find the computational efficiency of WBM, the relative prediction error defined in Eq. (29) is introduced. The convergence analysis of numerical predictive technique is to find out the relation between predictive precision and the computational cost. The predictive displacement amplitudes of point $R$ with two boundaries at 500 Hz are selected as the objectives for convergence analysis in this study:

29

$\epsilon =\frac{‖w-w_{ref}‖}{‖w_{ref}‖}.$

With $w_{ref}$ the referenced prediction obtained by fine meshed FE model.

Fig. 7 presents the convergence curves containing relative error and degree of freedom of both WBM and FEM. The compared result shows that the convergence rate of WBM is dramatically higher than FEM, which validates the higher computational efficiency of WBM. At this point, WBM is more available for mid-frequency problems contrasted with element based method.

Fig. 7Comparison of the convergence of FEM and WBM

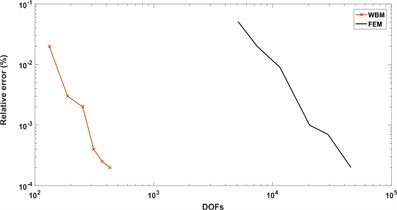
a) Simply supported boundary

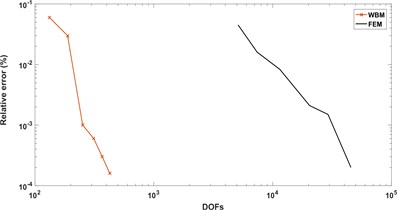
b) Clamped boundary

5. Conclusions

A novel prediction technique based on WBM for steady-state response of orthotropic plate is proposed. The new wavenumber parameters of wave function are derived and the particular solution for infinite orthotropic plate is introduced. The methodology of presented approach is validated by numerical examples with different boundary conditions. The outstanding computational accuracy and efficiency of WBM is verified by the comparison with FEM. And the vibro-acoustic prediction of complex geometry with orthotropic material based on wave based technique is to be studied on next stage.