A unified solution for free vibration of orthotropic annular sector thin plates with general boundary conditions, internal radial line and circumferential arc supports

Shi, Dongyan; Lv, Xiuhai; Wang, Qingshan; Liang, Qian

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2016

Check for updates

A unified solution for free vibration of orthotropic annular sector thin plates with general boundary conditions, internal radial line and circumferential arc supports

Dongyan Shi¹

Xiuhai Lv²

Qingshan Wang³

Qian Liang⁴

^{1, 2, 3, 4}College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin, P. R. China

^{1, 2, 3, 4}Department of Electrical and Mechanical Engineering, Heilongjiang Agricultural Engineering Vocational College, Harbin, P. R. China

Corresponding Author:

Qingshan Wang

Cite the article Download PDF

Downloads 1197

Abstract

In this paper, a modified Fourier-Ritz approach is adopted to analyze the free vibration of orthotropic annular sector thin plates with general boundary conditions, internal radial line and circumferential arc supports. In the present method, regardless of boundary conditions, the displacements of the sector plates are invariantly expressed as a standard Fourier cosine series and several auxiliary closed-form functions. These auxiliary functions are introduced to eliminate any potential discontinuities of the original displacement function and its derivatives throughout the whole domain including its edges, and then to effectively enhance the convergence of the results. Since the displacement field is constructed to be adequately smooth in the whole solution domain, an accurate solution can be obtained by using Ritz procedure based on the energy functions of the sector plates. The excellent accuracy and reliability of the current solutions are compared with the results found in the literature, and numerous new results for annular sector plates with various boundary conditions are presented. New results are obtained for annular sector plates subjected to elastic boundary restraints and arbitrary internal radial line and circumferential arc supports in both directions, and they may be served as benchmark solutions for future researches.

1. Introduction

Orthotropic annular sector thin plates are widely used in many engineering applications such as ships, curved bridge decks, aeronautical and space structures and other industrial applications due to their excellent engineering features. The orthotropic annular sector thin plates in these applications can be subjected to various boundary conditions, such as classical restraints, elastic supports and their combinations. In addition, the internal radial line and circumferential arc supports may be placed to reduce the magnitude of dynamic and static stresses and displacements of the plates as well as satisfy special functional requirements. Therefore a thorough understanding of the vibration behaviors of orthotropic annular sector thin plates with general boundary restraints, internal radial line and circumferential arc supports is of great interest for the designers to realize proper and comparatively accurate design of machines and structures.

In recent decades, the wide use of annular sector thin plate structures has motivated a huge amount of research efforts in developing the more accurate and applicable model and methods for analyzing their dynamic behaviors. Onoe [1] presented a mathematical method on basis of Love’s theory for contour vibrations of isotropic circular plates. Mcgee et al. [2] used a novel Ritz method to analyze free vibration of the sectorial plate with complete free boundary conditions. Wang and Thevendran [3] employed the Rayleigh-Ritz method to solve the free vibration problem of annular plates with internal axisymmetric supports. Wang et al. [4] extended the differential quadrature method to study the free vibration analysis of annular plates with classical boundary conditions. Later, Wang et al. [5] developed the differential quadrature method to analyze the free vibration of circular annular plates with classical boundary conditions and non-uniform thickness. Furthermore, Wang [6, 7] extended the differential quadrature method to analyze the free vibration of thin sector plates with various sector angles and six combinations of classical boundary conditions. Irie et al. [8] employed Ritz method to the free vibration of ring-shaped polar-orthotropic sector plates with classical boundary conditions. Singh et al. [9] used Rayleigh-Ritz method to analyze the transverse vibrations of circular plates with variable thickness and classical boundary conditions. Wong et al. [10] investigated the sensitivity of changes in displacement mode shapes of annular plates relative to the hole size and obtained approximations to frequencies and mode shapes of circular plates with variable thickness by using mode subtraction method. Houmat [11] presented a sector Fourier p-element on basis of finite element method for free vibration analysis of sectorial plates with classical boundary conditions. Chen et al. [12] applied a meshless method for free vibration analysis of circular and rectangular clamped plates with clamped boundary condition. Seok and Tiersten [13, 14] presented a variational approximation procedure for free vibration analysis of annular sector cantilever plates. Aghdam et al. [15] performed bending analysis of thin annular sector plates with clamped boundary condition by extended Kantorovich method. Li [16] employed finite strip method to study the free vibration of circular and annular sectorial thin plates subject to classical boundary conditions. Kim and Yoo [17] utilized a novel analytical solution to flexural responses of annular sector thin plates with classical boundary conditions. Mirtalaie and Hajabasi [18] studied the free vibration of annular sector thin plates with classical boundary conditions by using differential quadrature method.

A review of the scientific literature in this field reveals that the majority of the existing free vibration investigation mainly focused on the isotropic annular sector plate which has the same material property along different directions, while the reported work on the free vibration of the orthotropic annular sector thin plate is little. Most of the contributions on free vibration analysis of orthotropic annular sector thin plates with classical boundary supports are confined. In addition, orthotropic annular sector thin plates with internal radial line and circumferential arc supports are widely encountered in the engineering practices. Without these intermediate supports, the plates may undergo large deformation and acute shaking and eventually lead to structural failure. The only work focused on this subject is that Liew et al. [19] presented the vibrations of Thick isotropic annular sector plates with classical boundary conditions. However, a variety of possible elastic boundary condition cases which may not always be classical in nature can be encountered in practice. The existing solution procedures are often only customized for a specific set of different boundary conditions, and thus typically require constant modifications of the trial functions and corresponding solution procedures to adapt to different boundary cases. Therefore, the use of the existing solution procedures will result in very tedious calculations and be easily inundated with various classical boundary conditions and their combinations. To the best of authors’ knowledge, there are no reported solutions on the free vibration of orthotropic annular sector thin plates with general boundary conditions, internal radial line and circumferential arc supports in the literature. Therefore, it is necessary and of great significance to develop a unified, efficient and accurate formulation which is capable of universally dealing with orthotropic annular sector thin plates subjected to general boundary conditions, internal radial line and circumferential arc supports.

The purpose of the present study is to develop an efficient and accurate solution for free vibration analysis of orthotropic annular sector thin plates subjected to general boundary restraints, internal radial line supports, circumferential arc supports. In a previous study, a modified Fourier series technique proposed by Li [20, 21] is widely used in the vibrations of plates and shells with general boundary conditions by Ritz method, e.g., [22-30]. Therefore, the present work can be considered the combination of the modified Fourier series technique and Ritz method to present a modified Fourier-Ritz approach for free vibration of orthotropic annular sector thin plates subjected to general boundary conditions, internal radial line and circumferential arc supports. Under the current framework, regardless of boundary conditions, the displacements of the sector plates are invariantly expressed as a standard Fourier cosine series and several auxiliary closed-form functions. These auxiliary functions are introduced to eliminate any potential discontinuities of the original displacement function and its derivatives, throughout the whole domain including its edges, and then to effectively enhance the convergence of the results. Since the displacement field is constructed to be adequately smooth in the whole solution domain, an accurate solution can be obtained by using Ritz procedure based on the energy functions of the sector plates. The excellent accuracy and reliability of the current solutions are compared with the results found in the literature, and numerous new results for annular sector plates with various boundary conditions are presented. New results are obtained for annular sector plates subjected to elastic boundary restraints and arbitrary internal radial line and circumferential arc supports in both directions, and they may serve as benchmark solutions for future researches.

2. Theoretical formulations

2.1. Description of the model

Fig. 1 shows a orthotropic annular sector thin plate with uniform thickness $h$ , inner radius $a$ , outer radius $b$ , width $R$ of plate in the radial direction and sector angle $ϕ$ . The geometry and dimensions are defined in an orthogonal cylindrical coordinate system $(r, θ, z)$ . A local coordinate system $(s, θ, z)$ is also shown in the Fig. 1, which will be used in the analysis. Since the main focus of this paper is to develop a unified solution for the vibration analysis of orthotropic annular sector thin plates with general boundary conditions, thus, in order to satisfy the request, the artificial spring boundary technique is adopted here, in which each boundary of a plate is assumed to be restrained by one group of linear springs ( $k_{w}$ ) and one group of rotational springs ( $K_{r}$ ) to simulate the given or typical boundary conditions. The stiffness of the boundary springs can take any value from zero to infinity. By assigning the stiffness of the boundary springs with various values, it is equivalent to impose different boundary forces on the mid-plane of the plate. For example, the clamped boundary conditions are essentially obtained by setting the spring stiffness substantially larger than the bending rigidity of the plate.

2.2. Governing equations and boundary conditions

The governing equation of motion for the free vibration of orthotropic annular sector thin plates can be written as:

1

D_{11} \frac{\partial^{4} w}{\partial s^{4}} + 2 D_{12} \frac{1}{{(s + a)}^{2}} \frac{\partial^{4} w}{\partial s^{2} \partial θ^{2}} + D_{22} \frac{1}{{(s + a)}^{4}} \frac{\partial^{4} w}{\partial θ^{4}} + 2 D_{11} \frac{1}{s + a} \frac{\partial^{3} w}{\partial s^{3}}

- 2 D_{12} \frac{1}{{(s + a)}^{3}} \frac{\partial^{3} w}{\partial s \partial θ^{2}} - D_{22} \frac{1}{{(s + a)}^{2}} \frac{\partial^{2} w}{\partial s^{2}} + 2 (D_{22} + D_{12}) \frac{1}{{(s + a)}^{4}} \frac{\partial^{2} w}{\partial θ^{2}}

+ D_{22} \frac{1}{{(s + a)}^{3}} \frac{\partial w}{\partial s} - ρ h ω^{2} w^{2} = 0,

where $w$ is the sector plate deflection, $D_{i j}$ are the standard bending rigidities in the classical lamination theory. For an orthotropic annular sector thin plate, the stiffness constants are related to the lamina engineering constants and the plate thickness as:

2

D_{11} = \frac{E_{r} h^{3}}{12 (1 - μ_{r} μ_{θ})},

3

D_{22} = \frac{E_{θ} h^{3}}{12 (1 - μ_{r} μ_{θ})},

4

D_{12} = \frac{μ_{r} E_{θ} h^{3}}{12 (1 - μ_{r} μ_{θ})},

5

D_{66} = \frac{G_{r θ}}{12} h^{3} .

In terms of the flexural displacement, the bending and twisting moment and transverse shearing forces can be expressed as:

6

M_{r} = - D_{11} \frac{\partial^{2} w}{\partial s^{2}} - D_{12} \frac{1}{s + a} (\frac{\partial w}{\partial s} + \frac{1}{s + a} \frac{\partial^{2} w}{\partial θ^{2}}),

7

M_{θ} = - D_{22} \frac{1}{s + a} (\frac{\partial w}{\partial s} + \frac{1}{s + a} \frac{\partial^{2} w}{\partial θ^{2}}) - D_{12} \frac{\partial^{2} w}{\partial s^{2}},

8

M_{r θ} = - 2 D_{66} \frac{1}{s + a} (\frac{\partial^{2} w}{\partial s \partial θ} - \frac{1}{s + a} \frac{\partial w}{\partial θ}),

9

Q_{r} = - D_{11} \frac{\partial^{3} w}{\partial s^{3}} - (D_{12} + 4 D_{66}) (\frac{1}{{(s + a)}^{2}} \frac{\partial^{3} w}{\partial s \partial θ^{2}} - \frac{1}{{(s + a)}^{2}} \frac{\partial^{2} w}{\partial θ^{2}}),

10

Q_{θ} = - D_{22} \frac{1}{{(s + a)}^{3}} \frac{\partial^{2} w}{\partial θ^{3}}

- (D_{12} + 4 D_{66}) (\frac{1}{(s + a)} \frac{\partial^{3} w}{\partial s^{2} \partial θ} - \frac{2}{{(s + a)}^{2}} \frac{\partial^{2} w}{\partial s \partial θ} + \frac{2}{{(s + a)}^{3}} \frac{\partial w}{\partial θ}) .

Fig. 1Schematic diagram of annular sector thin plate with arbitrary boundary condition

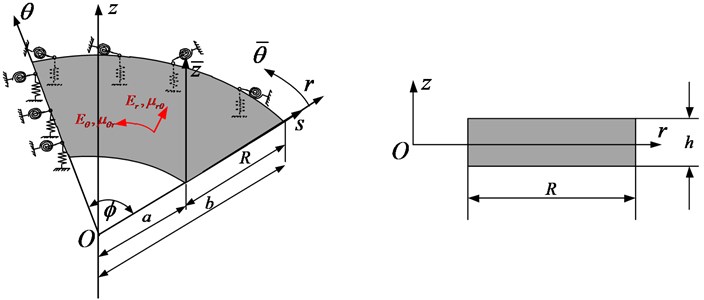
In this study, the general boundary conditions along each edge will be described in terms of two restraining springs, a linear spring $k_{γ}$ and a rotational spring $K_{γ}$ , where subscripts $γ = s_{0}$ , $s_{1}$ , $θ_{0}$ and $θ_{1}$ represent the springs at the boundary edges of the plate respectively, as shown in Fig. 1. Accordingly, the boundary conditions become:

11

s = 0 : \{\begin{array}{l} Q_{r} + k_{s_{0}}, w = 0, \\ M_{r} + K_{s_{0}}, \frac{\partial w}{\partial s} = 0, \end{array}

12

s = R : \{\begin{array}{l} Q_{r} - k_{s_{1}}, w = 0, \\ M_{r} - K_{s_{1}}, \frac{\partial w}{\partial s} = 0, \end{array}

13

θ = 0 : \{\begin{array}{l} Q_{θ} + k_{θ_{0}}, w = 0, \\ M_{θ} + K_{θ_{0}} \frac{1}{(s + a)}, \frac{\partial w}{\partial θ} = 0, \end{array}

14

θ = ϕ : \{\begin{array}{l} Q_{θ} - k_{θ_{1}}, w = 0, \\ M_{θ} - K_{θ_{1}} \frac{1}{(s + a)}, \frac{\partial w}{\partial θ} = 0 . \end{array}

Eqs. (11)-(14) represent a set of general boundary conditions. By setting the spring stiffnesses to appropriate values, all the classical homogeneous boundary conditions can be readily simulated.

From Eqs. (6)-(10), the boundary conditions can be finally written as:

At $s =$ 0:

15

k_{s_{0}} w = D_{11} \frac{\partial^{3} w}{\partial s^{3}} + (D_{12} + 4 D_{66}) (\frac{1}{{(s + a)}^{2}} \frac{\partial^{3} w}{\partial s \partial θ^{2}} - \frac{1}{{(s + a)}^{2}} \frac{\partial^{2} w}{\partial θ^{2}}),

16

K_{s_{0}} \frac{\partial w}{\partial s} = D_{11} \frac{\partial^{2} w}{\partial s^{2}} + D_{12} \frac{1}{s + a} (\frac{\partial w}{\partial s} + \frac{1}{s + a} \frac{\partial^{2} w}{\partial θ^{2}}) .

At $s = R$ :

17

k_{s_{1}} w = - D_{11} \frac{\partial^{3} w}{\partial s^{3}} - (D_{12} + 4 D_{66}) (\frac{1}{{(s + a)}^{2}} \frac{\partial^{3} w}{\partial s \partial θ^{2}} - \frac{1}{{(s + a)}^{2}} \frac{\partial^{2} w}{\partial θ^{2}}),

18

K_{s_{1}} \frac{\partial w}{\partial s} = - D_{11} \frac{\partial^{2} w}{\partial s^{2}} - D_{12} \frac{1}{s + a} (\frac{\partial w}{\partial s} + \frac{1}{s + a} \frac{\partial^{2} w}{\partial θ^{2}}) .

At $θ =$ 0:

19

k_{θ_{0}} w = D_{22} \frac{1}{{(s + a)}^{3}} \frac{\partial^{2} w}{\partial θ^{3}}

+ (D_{12} + 4 D_{66}) (\frac{1}{(s + a)} \frac{\partial^{3} w}{\partial s^{2} \partial θ} - \frac{2}{{(s + a)}^{2}} \frac{\partial^{2} w}{\partial s \partial θ} + \frac{2}{{(s + a)}^{3}} \frac{\partial w}{\partial θ}),

20

K_{θ_{0}} \frac{1}{(s + a)} \frac{\partial w}{\partial θ} = D_{22} \frac{1}{s + a} (\frac{\partial w}{\partial s} + \frac{1}{s + a} \frac{\partial^{2} w}{\partial θ^{2}}) + D_{12} \frac{\partial^{2} w}{\partial s^{2}} .

At $θ = ϕ$ :

21

k_{θ_{1}} w = - D_{22} \frac{1}{{(s + a)}^{3}} \frac{\partial^{2} w}{\partial θ^{3}}

- (D_{12} + 4 D_{66}) (\frac{1}{(s + a)} \frac{\partial^{3} w}{\partial s^{2} \partial θ} - \frac{2}{{(s + a)}^{2}} \frac{\partial^{2} w}{\partial s \partial θ} + \frac{2}{{(s + a)}^{3}} \frac{\partial w}{\partial θ}),

22

K_{θ_{1}} \frac{1}{(s + a)} \frac{\partial w}{\partial θ} = - D_{22} \frac{1}{s + a} (\frac{\partial w}{\partial s} + \frac{1}{s + a} \frac{\partial^{2} w}{\partial θ^{2}}) - D_{12} \frac{\partial^{2} w}{\partial s^{2}} .

2.3. Admissible displacement functions

Mathematically, it is often desired to express the displacement, $w (r, θ)$ , in the form of a Fourier series expansion because Fourier functions constitute a complete set and exhibit an excellent numerical stability. Unfortunately, the conventional Fourier series expression will generally have a convergence problem along the boundary edges except for a few simple boundary conditions. In addition, without being uniformly convergent, the derivatives of a Fourier series cannot be obtained simply through term-by-term differentiation. To overcome these problems, the displacement function will be here expressed as a more robust form of Fourier series expansion:

23

w (s, θ, t) = \{\sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} A_{m n} c o s λ_{R m} s c o s λ_{ϕ n} θ + \sum_{l = 1}^{4} ζ_{l} (θ) \sum_{m = 0}^{\infty} a_{m}^{l} c o s λ_{R m} s

+ \sum_{l = 1}^{4} χ_{l} (s) \sum_{n = 0}^{\infty} b_{n}^{l} c o s λ_{ϕ n} θ\} e^{j ω t},

where the eight supplementary terms are introduced to deal with any possible discontinuities or jumps at the boundaries which are potentially associated with the displacement function and its derivatives when they are periodically extended onto the entire solution domain. It should be noted that these discontinuities are not inherently related to the displacement function over the solution domain; instead they are the artifact resulting from the Fourier series representation of the displacement solution.

The four $ζ$ -functions in the $θ$ direction and $χ$ -functions in the $s$ direction in Eq. (23) are here chosen as:

24

ζ_{1} (θ) = \frac{ϕ}{2 π} s i n (\frac{π θ}{2 ϕ}) + \frac{ϕ}{2 π} s i n (\frac{3 π θ}{2 ϕ}),

25

ζ_{2} (θ) = - \frac{ϕ}{2 π} c o s (\frac{π θ}{2 ϕ}) + \frac{ϕ}{2 π} c o s (\frac{3 π θ}{2 ϕ}),

26

ζ_{3} (θ) = \frac{ϕ^{3}}{π^{3}} s i n (\frac{π θ}{2 ϕ}) - \frac{ϕ^{3}}{2 π^{3}} s i n (\frac{3 π θ}{2 ϕ}),

27

ζ_{4} (θ) = \frac{ϕ^{3}}{π^{3}} c o s (\frac{π θ}{2 ϕ}) - \frac{ϕ^{3}}{2 π^{3}} c o s (\frac{3 π θ}{2 ϕ}),

28

χ_{1} (s) = \frac{R}{2 π} s i n (\frac{π s}{2 R}) + \frac{R}{2 π} s i n (\frac{3 π s}{2 R}),

29

χ_{2} (s) = - \frac{R}{2 π} c o s (\frac{π s}{2 R}) + \frac{R}{2 π} c o s (\frac{3 π s}{2 R}),

30

χ_{3} (s) = \frac{R_{}^{3}}{π^{3}} s i n (\frac{π s}{2 R}) - \frac{R_{}^{3}}{2 π^{3}} s i n (\frac{3 π s}{2 R}),

31

χ_{4} (s) = \frac{R_{}^{3}}{π^{3}} c o s (\frac{π s}{2 R}) - \frac{R_{}^{3}}{2 π^{3}} c o s (\frac{3 π s}{2 R}) .

It is easy to verify that their first and third derivatives are mostly equal to zero along the boundary edges except for:

32

ζ_{1}^{'} (0) = ζ_{2}^{'} (ϕ) = ζ_{3}^{'''} (0) = ζ_{4}^{'''} (ϕ) = 1,

33

χ_{1}^{'} (0) = χ_{3}^{'} (R) = χ_{3}^{'''} (0) = χ_{4}^{'''} (R) = 1 .

It can be proven mathematically that the series expression in Eq. (23) is able to expand and uniformly converge to any function $Θ (r, θ) \in C^{3}$ for $\forall (x, y) \in D : ([0, R] \times [0, ϕ])$ . Also, this series can be simply differentiated, through term-by-term, to obtain the uniformly convergent series expansions for up to the fourth-order derivatives. Mathematically, an exact displacement (or classical) solution is a particular function $w (r, θ) \in C^{3}$ for $\forall (x, y) \in D$ which satisfies the governing equation at each field point and the boundary conditions at every boundary point.

2.4. Solution procedure

Once the admissible displacement functions and energy functions of the sector plate are established, the following task is to determine the coefficients in the admissible functions. Because of its simplicity and high accuracy, Ritz method is widely used in the vibration analysis of structural elements as a very powerful tool. In the Ritz method, the solutions can be obtained by minimizing the energy functional with respect to the coefficients of the admissible functions.

The strain energy of the sector plate is given as:

34

U_{p} = \frac{1}{2} \int_{o}^{R} \int_{0}^{ϕ} \{D_{11} {(\frac{\partial^{2} w}{\partial s^{2}})}^{2} + D_{22} {(\frac{1}{s + a} \frac{\partial w}{\partial s} + \frac{1}{{(s + a)}^{2}} \frac{\partial^{2} w}{\partial θ^{2}})}^{2} + 2 D_{12} \frac{\partial^{2} w}{\partial s^{2}} (\frac{1}{s + a} \frac{\partial w}{\partial s}

+ \frac{1}{{(s + a)}^{2}} \frac{\partial^{2} w}{\partial θ^{2}}) + 4 D_{66} (\frac{1}{s + a} \frac{\partial^{2} w}{\partial s \partial θ} - \frac{1}{{(s + a)}^{2}} \frac{\partial w}{\partial θ})\} (s + a) d s d θ .

By neglecting the rotary inertia, the kinetic energy of an orthotropic annular sector thin plate can be written as:

35

T = \frac{1}{2} ρ h ω^{2} \int_{o}^{R} \int_{0}^{ϕ} w^{2} (s + a) d s d θ .

As mentioned in Sections 2.1 and 2.2, each boundary of a sector plate is assumed to be restrained by one group of linear springs ( $k_{w}$ ) and one group of rotational springs ( $K_{r}$ ) to simulate the given or typical boundary conditions. Therefore, the deformation strain energy ( $U_{b s}$ ) stored in the boundary springs during vibration can be defined as:

36

U_{b s} = \frac{1}{2} \int_{0}^{ϕ} [a {\{k_{s_{0}} w^{2} + K_{s_{0}} {(\frac{\partial w}{\partial s})}^{2}\}}_{s = 0} + b {\{k_{s_{1}} w^{2} + K_{s_{1}} {(\frac{\partial w}{\partial s})}^{2}\}}_{s = R}] d θ

+ \frac{1}{2} \int_{0}^{R} [a {\{k_{θ_{0}} w^{2} + K_{θ_{0}} {(\frac{1}{s + a} \frac{\partial w}{\partial θ})}^{2}\}}_{θ = 0} + b {\{k_{θ_{1}} w^{2} + K_{θ_{1}} {(\frac{1}{s + a} \frac{\partial w}{\partial θ})}^{2}\}}_{θ = ϕ}] d s .

The Lagrangian functional ( $L$ ) of the plates during vibration can be expressed in terms of the energy expressions:

37

L = T - U_{p} - U_{b s} .

Substituting Eqs. (34)-(36) and Eq. (23) into Eq. (37) and performing the Ritz procedure with respect to each unknown coefficient, the equations of motion for plates can be yielded and are given in the matrix form:

38

\{K - ω^{2} M\} G = 0,

where:

39

G_{u} = \{\begin{array}{l} A_{00}, A_{01}, \dots, A_{m' 0}, A_{m' 1}, \dots, A_{m' n'}, \dots, A_{M N}, \\ a_{0}^{1}, \dots, a_{M}^{1}, a_{0}^{4}, \dots, a_{M}^{4}, b_{0}^{1}, \dots, b_{N}^{1}, b_{0}^{4}, \dots b_{N}^{4} \end{array}\} .

In Eq. (38), the $K$ is the stiffness matrix of the plate, and the $M$ is the mass matrix. For conciseness, the detailed expression for stiffness and mass matrices will not be shown here. By solving the Eq. (38), the frequencies (or eigenvalues) of orthotropic annular sector thin plates can be readily obtained and the mode shapes can be yielded by substituting the corresponding eigenvectors into series representations of displacement.

3. Numerical results and discussion

In this section, a systematic comparison between the current solutions and other methods is carried out to validate the excellent accuracy, reliability and feasibility of the present method. Unless otherwise stated, the non-dimensional $Ω = ω b^{2} / {(ρ_{1} h_{1} / D_{11})}^{1 / 2}$ is used in the presentation, and the material and geometry properties of orthotropic annular sector thin plates under consideration are: $ρ =$ 7800 kg/m³, $E_{θ} =$ 70 GPa, $E_{r} =$ 40 $E_{θ}$ , $G_{r θ} =$ 7.3 GPa, $μ_{r} =$ 0.3, $ϕ =$ 90, $b =$ 1 m, $b / a =$ 2 and $h / b =$ 0.005.

3.1. Determination of the boundary spring stiffness

In the present work, the general boundary conditions of the structure are implemented by introducing artificial spring boundary technique to separately simulate the boundary forces and displacements. As previously mentioned, the case of general boundary conditions of the plates can be easily simulated by assigning proper stiffness values to the boundary springs, for instance, a clamped boundary (C) can be readily achieved by simply setting the stiffness of the entire springs to be infinitely large. However, the “infinitely large” is represented by a sufficiently large number in actual calculations. Thus, effects of the spring stiffness of boundary springs on the modal characteristics should be investigated.

Effects of elastic boundary and coupling stiffness parameters on the non-dimensional frequency parameters $Ω$ of orthotropic annular sector thin plates are studied. A frequency parameter $Δ Ω$ which is defined as the difference of the non-dimensional frequency parameter $Ω$ to those of the elastic restraint parameters $Г_{λ (λ = w, r)}$ to 10^-2, i.e., $Δ Ω = Ω_{Г_{λ}} - Ω_{Г_{λ}} =$ 10^-2 is used in the calculation. The plates under consideration are completely clamped at boundaries $s =$ 0, $s = R$ , and free at boundary $θ =$ 0, while at edge $θ = ϕ$ , the plates are elastically supported by only one group of spring component with stiffnesses varying from 10^-2 to 10¹⁶. In Fig. 2(a), the influences of the line springs $k_{w}$ on frequency parameters are given. It is shown that the frequency parameter almost stays unchanged when the non-dimensional stiffness of the liner springs $k_{2}$ is larger than 10⁹ or smaller than 10⁴. In Fig. 2(b), the influences of the rotation springs $k_{w}$ on frequency parameters are given. It is shown that the frequency curve changes greatly within the stiffness range from 10³ to 10⁸. Based on the analysis, it can be found the frequency parameters exist the large change as the stiffness parameters increase in the certain range.

In the following discussion, vibration frequencies and modal shapes of annular sector plates with arbitrary classical boundary conditions, general elastic boundary conditions and their combinations will be presented. Taking edge $s =$ 0 for example, the corresponding spring stiffness parameters for three types of classical boundary conditions and three types of elastic boundary conditions which are commonly encountered in engineering practices are given as follows:

40

\{\begin{array}{l} C : k_{s 0} = 1 0^{14} N/m, K_{s 0} = 1 0^{14} N m / r a d; S : k_{s 0} = 1 0^{14} N / m, K_{s 0} = 0 N m / r a d, \\ F : k_{s 0} = 0 N / m, K_{s 0} = 0 N m / r a d; E^{1} : k_{s 0} = 1 0^{6} N / m, K_{s 0} = 0 N m / r a d, \\ E^{2} : k_{s 0} = 0 N / m, K_{s 0} = 1 0^{6} N m / r a d; E^{3} : k_{s 0} = 1 0^{6} N / m, K_{s 0} = 1 0^{6} N m / r a d . \end{array}

The appropriateness of defining the classical boundary conditions in terms of boundary spring parameters will be proved by several examples in later sub-sections. For the sake of simplicity, a simple letter string is employed to represent the boundary condition of the annular sector plate, circular sector plate, annular plate and circular plate, such as the FCSE identifies the annular sector plate with $F$ , $C$ , $S$ and $E$ boundary conditions at boundaries $s =$ 0, $θ =$ 0, $s = R$ and $θ = ϕ$ , respectively.

3.2. Convergence study

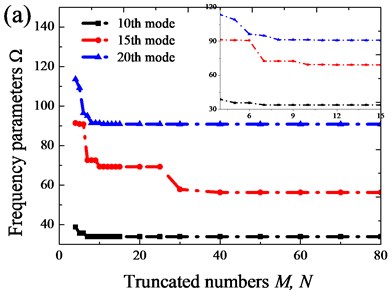
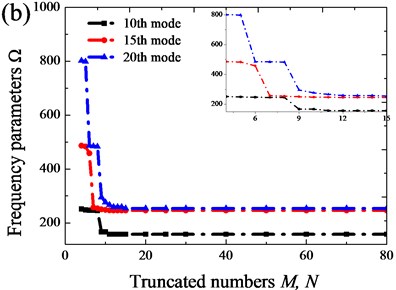
In this sub-section, the convergence of orthotropic annular sector plates with different boundary conditions is studied. The first eight frequency parameters $Ω$ for CCCC and FFFF orthotropic annular sector plates with different truncated number $M$ and $N$ (i.e. $M = N =$ 8-14) are given in Table 1. The Table shows the proposed method has fast convergence. The maximum discrepancy for the worst case between the truncated configuration $M =$ 12 and $M =$ 14 is less than 0.004 %. In order to fully illustrate the convergence of the present method, the frequency parameters $Ω$ of the higher mode (10th, 15th and 20th) with various truncated numbers $M$ , $N$ subjected to CCCC and FFFF boundary conditions are shown in Fig. 3. The highly desired convergence characteristics are observed: (a) sufficiently accurate results can be obtained with only a small number of terms in the series expansions; (b) the solution is consistently refined as more terms are included in the expansions; (c) the frequency parameters for higher-order modes tend to converge slower. Thus, an adequate truncation number should be dictated by the desired accuracy of the interesting largest natural frequencies. In view of the excellent numerical behavior of the current solution, the truncation numbers will be simply set as $M = N =$ 12 in the following calculations. To further validate the accuracy and reliability of the current solution, more numerical examples will be presented.

Fig. 2Variation of the frequency parameters Ω versus the elastic boundary restraint parameters for annular sector plate: a) transverse spring stiffness; b) rotation spring stiffness

Variation of the frequency parameters Ω versus the elastic boundary restraint parameters for annular sector plate: a) transverse spring stiffness; b) rotation spring stiffness

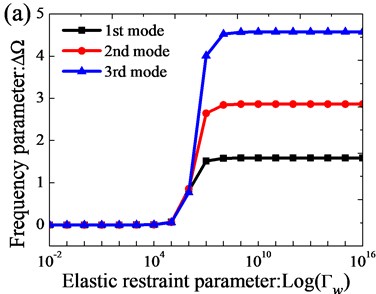
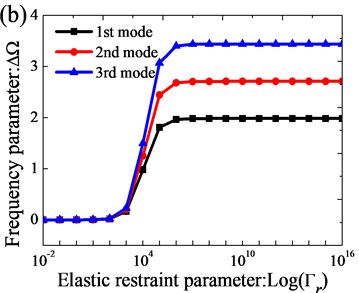
Fig. 3Variations of frequency parameter Ω with respect to truncated number M and N: a) FFFF; b) CCCC

3.3. Orthotropic annular sector thin plates with general boundary conditions

The target of this sub-section is to validate whether the present method can fit to solve the free vibration of orthotropic annular sector thin plates with general boundary conditions. First, a verification study about the classical boundary conditions is carried out to validate the accuracy and reliability of present method. In Tables 2 and 3, the first eight frequency parameters $Ω$ with different classical boundary conditions for isotropic annular sector thin plates and orthotropic annular sector thin plates are presented, respectively. In order to compare, the reference results taken from Ref. [18] and obtained using an FEM (ABAQUS) model are also given there. A great agreement can be obtained from the comparison. Next, we will focus on the free vibration of orthotropic annular sector thin plates with general elastic restraints. In Table 4, the detail comparisons between results obtained by the present method and those provided by FEM solutions (ABAQUS) are presented, in which nine types of elastic boundary conditions including classical-elastic case and complete elastic case are included. It is obvious that the current results match very well with the referential data. Based on the above analysis, it implies that the current method is able to make correct predictions for the modal characteristics of orthotropic annular sector thin plates with not only classical boundary but also elastically restrained boundary.

Table 1Convergence of frequencies parameters Ω for annular sector plate with CCCC and FFFF boundary conditions

Boundary conditions	$M = N$	Mode number
Boundary conditions	$M = N$	1	2	3	4	5	6	7	8
CCCC	8	88.838	89.265	90.382	92.702	96.822	103.30	112.57	128.41
	9	88.838	89.265	90.382	92.702	96.823	103.30	112.58	124.78
	10	88.838	89.265	90.381	92.702	96.821	103.30	112.55	124.78
	11	88.838	89.265	90.381	92.702	96.820	103.30	112.55	124.76
	12	88.838	89.265	90.381	92.702	96.820	103.30	112.55	124.76
	13	88.838	89.265	90.381	92.702	96.820	103.30	112.55	124.76
	14	88.838	89.265	90.381	92.702	96.820	103.30	112.55	124.76
FFFF	8	2.3039	2.3588	5.5209	6.6546	10.370	13.820	16.793	24.198
	9	2.3017	2.3530	5.5201	6.6527	10.370	13.819	16.792	24.198
	10	2.3017	2.3530	5.5201	6.6526	10.370	13.819	16.792	24.197
	11	2.3013	2.3517	5.5199	6.6523	10.370	13.819	16.791	24.197
	12	2.3013	2.3517	5.5199	6.6522	10.370	13.819	16.791	24.197
	13	2.3012	2.3516	5.5199	6.6521	10.370	13.819	16.791	24.197
	14	2.3012	2.3516	5.5199	6.6521	10.370	13.819	16.791	24.197

Table 2Frequency parameters Ω for isotropic annular sector plate with different classical boundary conditions

Boundary conditions	Methods	Mode number
Boundary conditions	Methods	1	2	3	4	5	6	7	8
FSFS	Present	21.067	66.722	81.604	146.41	176.12	176.9	274.57	298.37
	DQM	21.067	66.722	81.604	146.41	176.12	176.9	–	–
	FEM	21.032	66.498	81.46	145.66	175.83	176.51	273.51	297.25
SSSS	Present	68.379	150.98	189.6	278.39	283.59	387.62	438.96	443.89
	DQM	68.379	150.98	189.6	278.39	283.59	387.62	–	–
	FEM	68.112	150.55	189.12	277.75	282.4	386.99	437.32	442.9
CSCS	Present	107.57	178.82	269.49	305.84	346.46	476.3	487.39	508.57
	DQM	107.57	178.82	269.49	305.84	346.46	476.3	–	–
	FEM	107.41	178.48	269.11	305.35	345.51	475.56	485.84	507.83

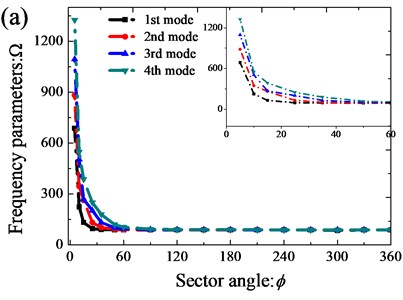
On the basis of verification of the presented method, next, the authors will study the influence of the stiffness ratio ( $E_{1} / E_{2}$ ) and sector angle ( $ϕ$ ) on the vibration characteristics of orthotropic annular sector thin plates with classical boundary and elastically restrained conditions. Fig. 4 depicts the variations of the first four frequency parameters $Ω$ of orthotropic annular sector thin plates along the variations of the stiffness ratio with CCCC and E³E³E³E³ boundary conditions. From the Fig. 4, the frequency parameters $Ω$ decrease rapidly and may reach their crest around a critical stiffness ratio, and beyond this range, the frequency parameters almost remain unchanged. The variations of the first four frequency parameters $Ω$ of orthotropic annular sector thin plates relative to the sector angle are given in Fig. 5. It is evident that the variations of the vibration characteristics of the orthotropic annular sector thin plate have the similar tendency with the variations relative to the stiffness ratio.

Table 3Frequency parameters Ω for orthotropic annular sector plate with different classical boundary conditions

Boundary conditions	Methods	Mode number
Boundary conditions	Methods	1	2	3	4	5	6	7	8
CCCC	Present	88.838	89.265	90.381	92.702	96.820	103.30	112.55	124.76
CCCC	FEM	89.033	89.443	90.530	92.823	96.935	103.46	112.85	125.32
SSSS	Present	39.424	39.945	41.486	44.882	50.885	59.861	71.742	86.191
SSSS	FEM	39.457	39.971	41.504	44.905	50.941	60.012	72.072	86.798
FFFF	Present	2.3013	2.3519	5.5199	6.6522	10.370	13.819	16.791	24.197
FFFF	FEM	2.3014	2.3514	5.5231	6.6528	10.384	13.828	16.834	24.257
CSCF	Present	88.732	88.842	89.202	90.143	92.145	95.79	101.66	110.21
CSCF	FEM	88.930	89.029	89.365	90.270	92.234	95.85	101.74	110.37

Table 4Frequency parameters Ω for orthotropic annular sector plate with various elastic boundary conditions

Boundary conditions	Methods	Mode number
Boundary conditions	Methods	1	2	3	4	5	6	7	8
CE¹CE¹	Present	88.791	89.014	89.566	90.561	92.087	94.513	98.550	104.90
CE¹CE¹	FEM	88.990	89.199	89.733	90.700	92.176	94.540	98.542	104.91
SE²SE²	Present	39.321	39.423	39.944	41.481	44.870	50.861	59.820	71.681
SE²SE²	FEM	39.356	39.455	39.971	41.499	44.891	50.916	59.971	72.010
FE³FE³	Present	1.8326	4.7181	4.7284	8.5757	9.8222	12.718	15.337	17.275
FE³FE³	FEM	1.8327	4.7354	4.7400	8.6054	9.9099	12.785	15.489	17.384
E²E¹E²E¹	Present	1.3032	4.8025	9.8634	15.543	21.385	27.578	34.504	36.093
E²E¹E²E¹	FEM	1.3037	4.8063	9.8763	15.567	21.422	27.642	34.611	36.077
E³E²E³E²	Present	11.561	11.643	12.666	16.101	22.051	29.423	37.753	39.744
E³E²E³E²	FEM	11.553	11.707	12.739	16.172	22.141	29.555	37.958	39.747
E¹E³E¹E³	Present	11.338	13.077	15.856	19.141	20.533	21.884	22.887	24.534
E¹E³E¹E³	FEM	11.284	13.045	15.850	19.164	20.427	21.868	22.921	24.759
E¹E¹E¹E¹	Present	11.032	12.212	15.039	18.793	20.373	21.338	22.881	24.137
E¹E¹E¹E¹	FEM	10.975	12.168	15.015	18.793	20.261	21.259	22.913	24.234
E²E²E²E²	Present	1.3226	5.0470	10.944	18.286	26.321	35.077	35.935	36.106
E²E²E²E²	FEM	1.3229	5.0506	10.960	18.328	26.408	35.239	35.942	36.135
E³E³E³E³	Present	11.892	13.416	16.195	19.872	24.922	31.443	39.178	39.986
E³E³E³E³	FEM	11.830	13.376	16.204	19.932	25.019	31.583	39.368	39.950

3.4. Orthotropic annular sector thin plates with line/arc supports

In the engineering practices, the plate structures are often restrained by internal line supports to reduce the magnitude of dynamic and static stresses and displacements of the structure or to satisfy special architectural and functional requirements. However, the research work on plates with internal line supports is scanty. Thus, in this paper, except the classical and general elastic boundary conditions, the authors also investigate the free vibration behaviors of orthotropic annular sector plates with internal radial line and circumferential arc supports. As shown in Fig. 4, the orthotropic annular sector plate is restrained by arbitrary internal radial line and circumferential arc supports. $r_{i}$ and $θ_{j}$ represent the position of the $i$ th and $j$ th internal radial line and circumferential arc supports along the $r^{-}$ and $θ^{-}$ directions, respectively. The displacement fields in the position of the line support satisfy $w (r_{i}, θ, t) =$ 0 and $w (r, θ_{i}, t) =$ 0. This condition can be readily obtained by introducing a group of continuously distributed linear springs at the location of each line/arc support and setting the stiffnesses of these springs equal to be infinite (which is represented by a very large number, 10¹⁴). Thus, the potential energy ( $P_{r a l s}$ ) stored in these springs is:

41

P_{r a l s} = \frac{1}{2} \int_{0}^{ϕ} \{\sum_{i = 1}^{M_{i}} k_{r i}^{i} w {(r_{i}, θ, t)}^{2} (r_{i} + a)\} d θ + \frac{1}{2} \int_{0}^{R} \{\sum_{j = 1}^{N_{j}} k_{θ j}^{j} w {(r, θ_{j}, t)}^{2}\} d s,

where $M_{i}$ and $N_{j}$ are the amount of circumferential arc supports and radial line in the $θ$ and $r$ directions. $k_{r i}^{i}$ and $k_{θ j}^{j}$ denote the corresponding circumferential arc supported and radial line springs distributed at $r = r_{i}$ and $θ = θ_{j}$ . By adding the potential energy $P_{r a l s}$ stored in the line/arc supported springs in the Lagrangian energy function (Eq. (37)) and carrying out the Ritz procedure, the characteristic equation for a orthotropic annular sector thin plates with arbitrary boundary conditions and internal radial line and circumferential arc supports is readily obtained.

Fig. 4Variation of the frequency parameters Ω versus the stiffness rations (E1/E2) for annular sector plate: a) CCCC; b) E3E3E3E3

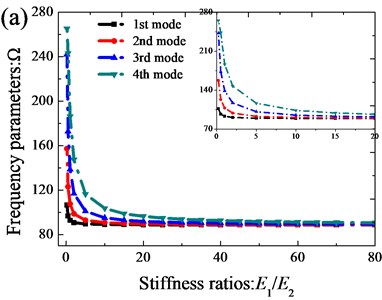
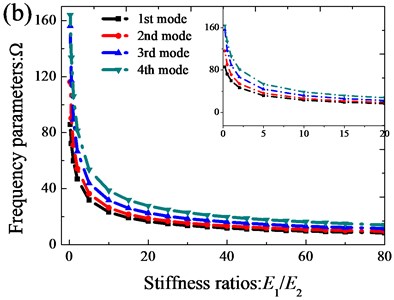
Fig. 5Variation of the frequency parameters Ω versus the sector angle for annular sector plate: a) CCCC; b) E3E3E3E3

In order to prove the validity of the present formulations for the vibration of orthotropic annular sector thin plates with internal radial line and circumferential arc supports, Table 5 presents the comparison of the first eight frequency parameters $Ω$ for sector plates with three classical boundary conditions, i.e. CCCC, SSSS, FFFF. For the purpose of stressing the effects of the line/arc supports, corresponding results for the considered annular sector plate without line/arc supports are also presented in the table. The benchmark results are provided by ABAQUS based on FEA method. From the table a consistent agreement of present results and referential date is seen. The discrepancy is very small and doesn’t exceed 0.61 % for the worst case. In addition, the table shows that the line/arc supports can increase the frequencies of the sector plate. Then, the influence of the locations of internal radial line and circumferential arc supports on the frequency of orthotropic annular sector plates is investigated. For simplicity of this research, when investigating the influence of the radial line support along $θ$ direction, the circumferential edges of the plates are under clamped boundary conditions and we only change the radial boundary conditions; on the contrary, when studying the effect of the circumferential arc supports along $s$ direction, the radial edges are with clamped boundary condition and only the boundary conditions of the circumferential edges vary. In Fig. 7, the variations of the fundamental frequency parameters $Ω$ of the considered sector plate with against the radial line support location parameter $θ_{1} / ϕ$ and against the circumferential arc support location parameter $R_{1} / R$ are depicted. Six types of edge conditions used in the investigation are: C-C, S-S, F-C, C-F, F-S, S-F. It is obvious that the frequency parameters of the sector plate are significantly affected by the position of the radial line and circumferential arc support, and this effect varies with the edge conditions.

Fig. 6Schematic diagram of an annular sector plate with arbitrary internal radial line and circumferential supports

Table 5Comparison of the first eight frequency parameters Ω for orthotropic annular sector thin plate with different line supports

Line supports	Boundary conditions	Methods	Mode number
Line supports	Boundary conditions	Methods	1	2	3	4	5	6	7	8
None	CCCC		20.453	20.552	20.809	21.343	22.291	23.783	25.913	28.724
	SSSS		9.0767	9.1966	9.5514	10.333	11.715	13.782	16.517	19.844
	FFFF		0.5298	0.5415	1.2709	1.5316	2.3875	3.1816	3.8658	5.5709
$\frac{R}{2}$	CCCC	Present	245.75	246.09	246.83	248.18	250.43	253.90	258.92	265.72
	CCCC	FEM	247.25	247.52	248.17	249.41	251.53	254.84	259.73	266.47
	SSSS	Present	157.85	158.20	158.99	160.50	163.08	167.11	172.92	180.65
	SSSS	FEM	158.40	158.73	159.46	160.90	163.41	167.38	173.17	180.95
	FFFF	Present	1.3847	2.6689	5.9102	11.2125	18.490	26.815	35.130	43.346
	FFFF	FEM	1.3822	2.6663	5.9101	11.2192	18.518	26.875	35.226	43.498
$\frac{R}{2}, \frac{ϕ}{2}$	CCCC	Present	246.09	246.26	248.18	248.97	253.90	256.03	265.72	270.00
	CCCC	FEM	247.52	247.68	249.41	250.17	254.84	256.85	266.47	270.36
	SSSS	Present	158.20	158.37	160.50	161.39	167.11	169.55	180.65	185.30
	SSSS	FEM	158.73	158.89	160.90	161.76	167.38	169.73	180.95	185.25
	FFFF	Present	2.6690	3.5863	11.212	14.306	26.815	30.980	43.346	47.782
	FFFF	FEM	2.6663	3.5829	11.219	14.304	26.875	30.992	43.498	47.812

Since the vibration results for internal radial line and circumferential arc supported orthotropic annular sector thin plates with arbitrary boundary conditions are very limited in the literature, some new results are calculated here, which can be used for benchmark results by researchers as well as reference datum for practicing engineers. In Table 6, the first six frequency parameters $Ω$ of the considered orthotropic annular sector thin plate subjected to as many as nine possible boundary conditions are presented. And four different line/arc support conditions are considered in the calculation. In addition, the lowest four mode shapes for the sector plate with CE¹CE¹ boundary condition presented in Table 6 are given in Fig. 8. These view mode shapes are served to enhance our understanding of the vibratory characteristics of the orthotropic annular sector thin plates with internal radial line and circumferential arc supports.

Fig. 7Variation of the frequency parameters Ω versus the radial support locations and arc support locations for annular sector plate with different boundary conditions

Variation of the frequency parameters Ω versus the radial support locations and arc support locations for annular sector plate with different boundary conditions

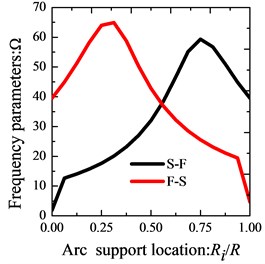
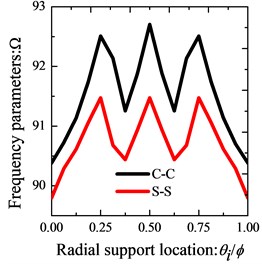
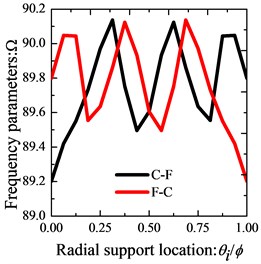
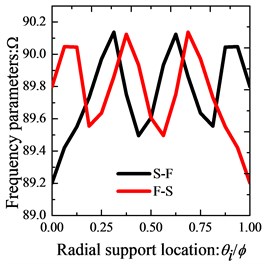
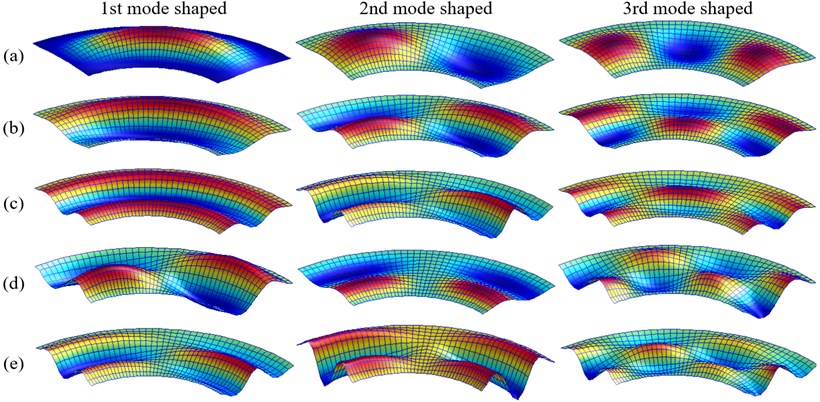
Fig. 8The lowest three modes shape for a CE1CE1 annular sector plate with various line supports: a) None; b) r1=R/2; c) r1=R/3, r2=2R/3; d) r1=R/2, θ1=ϕ/2; e) r1=R/3, θ1=ϕ/2, r2=2R/3

The lowest three modes shape for a CE1CE1 annular sector plate with various line supports: a) None; b) r1=R/2; c) r1=R/3, r2=2R/3; d) r1=R/2, θ1=ϕ/2; e) r1=R/3, θ1=ϕ/2, r2=2R/3

4. Conclusions

A modified Fourier-Ritz approach is presented for the free vibration analysis of orthotropic annular sector thin plates with general boundary conditions, internal radial line and circumferential arc supports. Under the current framework, the admissible displacement function of the plate, regardless of the boundary conditions, is expressed as a modified Fourier series, which is constructed as the linear superposition of a standard Fourier cosine series supplemented with auxiliary polynomial functions introduced to eliminate all the relevant discontinuities with the displacement and its derivatives at the edges and accelerate the convergence of series representations.

Table 6The first six frequency parameters Ω for orthotropic annular sector thin plates with different boundary conditions and various arc and radial line supports

Line supports	Mode	Boundary conditions
Line supports	Mode	CE¹CE¹	SE²SE²	FE³FE³	E²E¹E²E¹	E³E²E³E²	E¹E³E¹E³	E¹E¹E¹E¹	E²E²E²E²	E³E³E³E³
$r_{1} = \frac{R}{2}$	1	245.70	157.75	3.9791	35.594	39.409	20.539	20.376	35.461	39.610
	2	245.88	157.85	8.1532	36.210	39.541	21.763	21.291	35.606	40.312
	3	246.21	158.20	12.735	37.691	40.215	23.898	23.511	36.347	41.593
	4	246.74	158.99	18.006	40.130	42.167	27.154	26.993	38.479	43.746
	5	247.60	160.49	24.718	43.639	46.157	32.158	31.553	42.773	47.563
	6	249.04	163.06	32.362	48.710	52.248	38.581	37.234	49.212	53.392
$r_{1} = \frac{R}{3},$ $r_{2} = \frac{2 R}{3}$	1	454.35	355.14	71.101	115.53	117.55	75.70	75.66	115.47	117.63
	2	454.47	355.24	71.448	115.79	117.63	76.03	75.92	115.55	117.91
	3	454.72	355.56	72.082	116.31	117.95	76.64	76.52	115.87	118.40
	4	455.16	356.18	73.134	117.16	118.74	77.64	77.57	116.67	119.26
	5	455.87	357.23	74.895	118.48	120.29	79.34	79.17	118.24	120.80
	6	456.97	358.90	77.555	120.52	122.78	81.91	81.46	120.74	123.24
$r_{1} = \frac{R}{2},$ $θ_{1} = \frac{ϕ}{2}$	1	245.88	157.85	8.1532	36.210	39.541	21.763	21.291	35.606	40.312
	2	245.94	157.89	10.185	36.694	39.664	22.614	22.070	35.743	40.779
	3	246.74	158.99	18.006	40.130	42.167	27.154	26.993	38.479	43.746
	4	247.00	159.43	21.022	41.583	43.696	29.301	29.013	40.134	45.253
	5	249.03	163.06	32.362	48.710	52.248	38.581	37.234	49.212	53.392
	6	249.88	164.62	36.274	51.791	55.762	42.035	40.395	52.880	56.802
$r_{1} = \frac{R}{3},$ $θ_{1} = \frac{ϕ}{2},$ $r_{2} = \frac{2 R}{3}$	1	454.47	355.24	71.448	115.79	117.63	76.030	75.922	115.55	117.91
	2	454.50	355.26	71.657	115.92	117.67	76.228	76.095	115.59	118.04
	3	455.16	356.18	73.134	117.16	118.74	77.643	77.570	116.67	119.26
	4	455.31	356.42	73.818	117.63	119.26	78.300	78.205	117.20	119.80
	5	456.97	358.90	77.555	120.52	122.78	81.906	81.458	120.74	123.24
	6	457.49	359.74	79.145	121.74	124.22	83.437	82.829	122.20	124.67

The general boundary conditions of the sector plate are accounted for by using the artificial spring boundary technique, in which the elastic restraint stiffnesses can take any value from zero to infinity to better simulate many real-world boundary conditions. Ritz procedure is used to obtain the exact solution based on the energy functions of those structures. The convergence of the present solution is checked and the excellent accuracy is validated by the comparison with the existing results published in the literature and FEM solutions. Excellent agreements are obtained from these comparisons. The effects of elastic restraint parameters and locations of radial line and circumferential arc supports are also investigated and reported. New results for free vibration of orthotropic annular sector thin plates with various edge conditions and internal radial line and circumferential arc supports are presented, which may be used for benchmarking of researchers in the field.

References

Onoe M. Contour vibrations of isotropic circular plates. Journal of the Acoustical Society of America, Vol. 28, Issue 6, 1956, p. 1158-1162.

Search CrossRef
Mcgee O. G., Leissa A. W., Huang C. S. Vibrations of completely free sectorial plates. Journal of Sound and Vibration, Vol. 164, Issue 3, 1993, p. 565-569.

Search CrossRef
Wang C. M., Thevendran V. Vibration analysis of annular plates with concentric supports using a variant of Rayleigh-Ritz method. Journal of Sound and Vibration, Vol. 163, Issue 1, 1993, p. 137-149.

Search CrossRef
Wang X., Striz A. G., Bert C. W. Free-vibration analysis of annular plates by the Dq-method. Journal of Sound and Vibration, Vol. 164, Issue 1, 1993, p. 173-175.

Search CrossRef
Wang X., Yang J., Xiao J. On free vibration analysis of circular annular plates with non-uniform thickness by the differential quadrature method. Journal of Sound and Vibration, Vol. 184, Issue 3, 1995, p. 547-551.

Search CrossRef
Wang X. W., Wang Y. L. Free vibration analyses of thin sector plates by the new version of differential quadrature method. Computer Methods in Applied Mechanics and Engineering, Vol. 193, Issues 36-38, 2004, p. 3957-3971.

Search CrossRef
Wang X. W., Wang Y. L. Re-analysis of free vibration of annular plates by the new version of differential quadrature method. Journal of Sound and Vibration, Vol. 278, Issue 3, 2004, p. 685-689.

Search CrossRef
Irie T., Yamada G., Ito F. Free-vibration of polar-orthotropic sector plates. Journal of Sound and Vibration, Vol. 67, Issue 1, 1979, p. 89-100.

Search CrossRef
Singh B., Hassan S. M. Transverse vibration of a circular plate with arbitrary thickness variation. International Journal of Mechanical Sciences, Vol. 40, Issue 11, 1998, p. 1089-1104.

Search CrossRef
Wong W. O., Yam L. H., Li Y. Y., Law L. Y., Chan K. T. Vibration analysis of annular plates using mode subtraction method. Journal of Sound and Vibration, Vol. 232, Issue 4, 2000, p. 807-822.

Search CrossRef
Houmat A. A sector Fourier p-element applied to free vibration analysis of sectorial plates. Journal of Sound and Vibration, Vol. 243, Issue 2, 2001, p. 269-282.

Search CrossRef
Chen J. T., Chen I. L., Chen K. H., Lee Y. T., Yeh Y. T. A meshless method for free vibration analysis of circular and rectangular clamped plates using radial basis function. Engineering Analysis with Boundary Elements, Vol. 28, Issue 5, 2004, p. 535-545.

Search CrossRef
Seok J., Tiersten H. F. Free vibrations of annular sector cantilever plates. Part 1: out-of-plane motion. Journal of Sound and Vibration, Vol. 271, Issue 3, 2004, p. 757-772.

Search CrossRef
Seok J., Tiersten H. F. Free vibrations of annular sector cantilever plates. Part 2: in-plane motion. Journal of Sound and Vibration, VVol. 271, Issue 3, 2004, p. 773-787.

Search CrossRef
Aghdam M. M., Mohammadi M., Erfanian V. Bending analysis of thin annular sector plates using extended Kantorovich method. Thin-Walled Structures, Vol. 45, Issue 12, 2007, p. 983-990.

Search CrossRef
Yongqiang L., Jian L. Free vibration analysis of circular and annular sectorial thin plates using curve strip Fourier p-element. Journal of Sound and Vibration, Vol. 305, Issue 3, 2007, p. 457-466.

Search CrossRef
Kim K., Yoo C. H. Analytical solution to flexural responses of annular sector thin-plates. Thin-Walled Structures, Vol. 48, Issue 12, 2010, p. 879-887.

Search CrossRef
Hajabasi M. A., Mirtalaie S. H. Free vibration analysis of functionally graded thin annular sector plates using the differential quadrature method. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 225, Issue 3, 2011, p. 568-583.

Search CrossRef
Liew K. M., Kitipornchai S., Xiang Y. Vibration of annular sector mindlin plates with internal radial line and circumferential arc supports. Journal of Sound and Vibration, Vol. 183, Issue 3, 1995, p. 401-419.

Search CrossRef
Li W. L. Free vibrations of beams with general boundary conditions. Journal of Sound and Vibration, Vol. 237, Issue 4, 2000, p. 709-725.

Search CrossRef
Li W. L. Comparison of Fourier sine and cosine series expansions for beams with arbitrary boundary conditions. Journal of Sound and Vibration, Vol. 255, Issue 1, 2002, p. 185-194.

Search CrossRef
Du J., Li W. L., Jin G., Yang T., Liu Z. An analytical method for the in-plane vibration analysis of rectangular plates with elastically restrained edges. Journal of Sound and Vibration, Vol. 306, Issues 3-5, 2007, p. 908-927.

Search CrossRef
Du J. T., Liu Z. Li W. L., Zhang X., Li W. Free in-plane vibration analysis of rectangular plates with elastically point-supported edges. Journal of Vibration and Acoustics-Transactions of the ASME, Vol. 132, Issue 3, 2010, p. 031002.

Search CrossRef
Shi D., Wang Q., Shi X., Pang F. A series solution for the in-plane vibration analysis of orthotropic rectangular plates with non-uniform elastic boundary constraints and internal line supports. Archive of Applied Mechanics, Vol. 85, Issue 1, 2015, p. 51-73.

Search CrossRef
Shi X., Shi D., Li W., Wang Q. A unified method for free vibration analysis of circular, annular and sector plates with arbitrary boundary conditions. Journal of Vibration and Control, 2014.

Search CrossRef
Jin G., Ye T., Chen Y., Su Z., Yan Y. An exact solution for the free vibration analysis of laminated composite cylindrical shells with general elastic boundary conditions. Composite Structures, Vol. 106, 2013, p. 114-127.

Search CrossRef
Jin G., Ye T., Ma X., Chen Y., Su Z., Xie X. A unified approach for the vibration analysis of moderately thick composite laminated cylindrical shells with arbitrary boundary conditions. International Journal of Mechanical Sciences, Vol. 75, 2013, p. 357-376.

Search CrossRef
Chen Y., Jin G., Liu Z. Flexural and in-plane vibration analysis of elastically restrained thin rectangular plate with cutout using Chebyshev-Lagrangian method. International Journal of Mechanical Sciences, Vol. 89, 2014, p. 264-278.

Search CrossRef
Jin G., Ma X., Shi S., Ye T., Liu Z. A modified Fourier series solution for vibration analysis of truncated conical shells with general boundary conditions. Applied Acoustics, Vol. 85, 2014, p. 82-96.

Search CrossRef
Jin G., Ye T., Jia X., Gao S. A general Fourier solution for the vibration analysis of composite laminated structure elements of revolution with general elastic restraints. Composite Structures, Vol. 109, 2014, p. 150-168.

Search CrossRef

About this article

Received

22 August 2015

Accepted

29 October 2015

Published

15 February 2016

SUBJECTS

Modal analysis

Keywords

free vibration

orthotropic annular sector thin plates

general boundary conditions

internal circumferential arc supports

internal radial line supports

Ritz approach

Acknowledgements

The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (No. 51209052), Heilongjiang Province Youth Science Fund Project (No. QC2011C013) and Harbin Science and Technology Development Innovation Foundation of Youth (No. 2011RFQXG021).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.