A Unified method for vibration analysis of moderately thick annular, circular plates and their sector counterparts subjected to arbitrary boundary conditions

Ahad, Fazl e; Shi, Dongyan; Rehman, Anees Ur; Waqas, Hafiz M.

doi:10.21595/jve.2016.16834

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 December 2016

Check for updates

A Unified method for vibration analysis of moderately thick annular, circular plates and their sector counterparts subjected to arbitrary boundary conditions

Fazl e Ahad¹

Dongyan Shi²

Anees Ur Rehman³

Hafiz M. Waqas⁴

^{1, 2, 3, 4}College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin, China

Corresponding Author:

Fazl e Ahad

Cite the article Download PDF

Downloads 1719

WoS Core Citations 1

CrossRef Citations 1

Abstract

The vibrations of circular, annular and sector plates are different boundary value problems due to different edge conditions and thus have been treated separately using different solution algorithms and procedures. In this paper, a unified method is proposed for vibration analysis of moderately thick annular, circular plates and their sector counterparts with arbitrary boundary conditions. The unification of these plates is physically achieved by applying the coupling spring’s technique at the radial edges to ensure appropriate continuity conditions. Irrespective of the shape of the plate and the type of boundary conditions, each of the displacement function is expressed as a new form of trigonometric expansion with high convergence rate. Unlike most of the previous studies the current method can be universally applied to a wide range of vibration problems involving different shapes, boundary conditions, varying materials and geometric properties without modifying the solution algorithms and procedure. Furthermore, the current method can easily be applied to sector plates with an arbitrary inclusion angle of 2 $π$ . The accuracy, reliability and versatility of the proposed method are fully demonstrated with several numerical examples for different shapes of plates and under different boundary conditions.

1. Introduction

Circular, annular and their sectorial counterparts are important structural components widely used in many engineering fields like civil, mechanical and marine engineering. As far as previous literature is concerned different solution algorithms and procedures have been adopted to study their vibration characteristics. The main reason behind these different solution algorithms and procedures was difference in their geometries resulting in different edge conditions.

A lot of research work has been done to study their dynamic characteristics under different boundary conditions. The important and comprehensive review on this subject can be found in Leissa’s 1973 book. The initial study on vibrations of circular plates or disks was done by Deresiewicz and Mindlin [1]. Employing the classical thin plate theory and Mindlin plate theory, these two researchers studied the vibration characteristics of axially symmetric circular disks. This work was further extended by Soni et al. [2] to axisymmetric orthotropic non uniform circular discs. They carried out their research using the same Mindlin plate theory and Chebyshev collocation technique. This technique was later employed by Gupta et al. to polar orthotropic annular Mindlin plates with non-uniform thickness [3]. Using Finite Element Method and three-dimensional finite strip model, Cheung et.al studied the vibration characteristics of thick and thin sector plates subjected to different types of classical boundary conditions [4, 5]. Investigation on vibration characteristics of annular sector plates having internal radial line and circumferential arc supports was carried out by Xiang et al. [6-7]. In another study Xiang et al. used first order shear deformation theory and studied the vibration response of thick circular and annular plates with internal ring stiffeners [8]. Later he extended his research to stepped circular Mindlin plates by employing domain decomposition technique to study the vibration characteristics [9]. Another similar study was performed by B. Singh and S. M. Hassan [10]. They studied the out of plane vibrations of a circular plate with different thickness variation. They approximated the thickness polynomial by interpolating the sample points along the thickness of the plate. In another study a combination of Rayleigh-Ritz method and Lagrange multiplier method was developed by S. Kitipornchai et al. to study the vibration characteristics of arbitrary shaped plates with corner supports [11]. Exact solution for annular sector plates subjected to simply supported radial edge conditions and general boundary conditions at circular edges was obtained by McGee et al. [12] employing the Mindlin plate theory and using ordinary and modified Bessel functions of the first and second kind.

Differential quadrature method was employed by various researchers to study the vibration characteristics of sector plates, annular sector plates and solid circular plates. Extensive results were reported for these plates subjected to various sets of classical boundary conditions [13-15]. Huang et al. [16] employed Frobenius method on orthotropic sector plates and studied the effect of Young modulus and shear modulus on the vibration characteristics of these plates. In another important research on thick circular and annular plates with uniform, linear and quadratic change in thickness along the radial edge was performed by Jae Hoon Kang [17]. A similar three-dimensional study of thick annular and circular plates was carried out by J. So et al. [18] employing Rayleigh-Ritz method. In their research they used trigonometric functions and algebraic polynomial as admissible displacement functions along the circumferential and radial and axial coordinates respectively. Another three-dimensional study of annular and circular plates was performed by Zhou et.al. They employed Chebyshev-Ritz technique and used Chebyshev polynomial as admissible function. Later they extended the same Chebyshev-Ritz technique to annular sector plates [19, 20]. Another important three-dimensional investigation on annular plates resting on elastic foundation was done by Hashemi et al. They used polynomial-Ritz approach and studied the effect of cutout ratio, thickness to radius ratio and elastic foundation on the vibration characteristics of annular plates subjected to various combinations of classical boundary conditions [21].

Discrete singular convolution method was used by Civalek et.al to investigate the vibration characteristics of Mindlin annular plates and thick circular plates [22, 23]. Similarly employing the Mindlin plate theory and first order shear deformation theory, Jomehzadeh et.al investigated the transverse vibrations of isotropic sector plate and moderately thick annular sector plates subjected to simply supported boundary conditions and arbitrary boundary conditions at radial and circular edges respectively [24-25]. In plane free vibration analysis of isotropic homogeneous circular disks subjected to arbitrary boundary conditions at the inner and outer edges was investigated by Bashmal et al. by employing two-dimensional linear plane stress theory. In another study he employed Rayleigh-Ritz method to study the vibration characteristics of annular disk with point elastic support [26, 27]. Similarly, Ravari et al. investigated the in plane vibrations of orthotropic circular annular plates by using Helmholtz decomposition technique and separation of variables method [28].

In other similar studies on circular, annular and sector plates, Sari et al. [29] used Chebyshev collocation method to study the vibration characteristics of Mindlin annular plates with damaged boundary conditions. Similarly, Reddy’s higher order shear deformation theory was employed by Bisadi et.al and Es’Haghi [30, 31] to investigate the vibration characteristics of thick circular and annular plates subjected to different combinations of classical boundary conditions at edges. Employing the boundary restraining springs technique Shi et.al proposed a generalized Fourier series method to study the annular sector plates subjected to elastic boundary conditions at each edge [32-33]. Later X. Shi et al. [34] proposed a unified method for vibration analysis of circular, annular and their sector counterparts by employing coupling springs technique at the coupling edge. The same idea has been adopted here to develop a unified method to study the vibration characteristics of Mindlin circular, annular and their sector counter parts subjected to general elastic boundary conditions. The beauty of this method is that it does not require any modification in the procedure or solution algorithm to accommodate these different geometries and boundary conditions.

2. Theoretical formulation

2.1. Description of the model

Consider a moderately thick annular sector plate with internal radius $a$ , outer radius $b$ , thickness $h$ and width $R$ in the radial direction as shown in Fig. 1. The angle $ϕ$ represents the sector angle of the plate. The plate geometry and dimensions are defined in the cylindrical coordinate system $(r, ϕ, z)$ .

Fig. 1Geometry of moderately thick annular sector plate

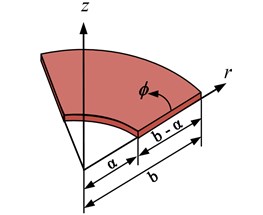
a)

b)

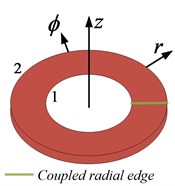
The elastic boundary conditions along the edges are specified using boundary spring technique. One translational and two rotational springs of arbitrary stiffness values are attached at each edge to simulate arbitrary boundary conditions. All the classical sets of boundary conditions can easily be achieved by varying the stiffness value of each spring from zero to an infinitely large number i.e. 10¹⁴. It can be seen in Fig. 2 that an annular plate can be obtained by annular sector plate when the sector angle becomes equal to 2 $π$ , a circular sector plate can be obtained from annular sector plate if the inner radius $a$ becomes equal to 0. Similarly, a circular plate can be obtained when the inclusion angle of the annular sector plate becomes equal to 2 $π$ and the inner radius $a$ also becomes equal to 0. Therefore, the solution algorithm and procedure will be developed in such a way that it can easily be applied to annular, circular and circular sector plates just by varying geometric parameters mentioned earlier.

Fig. 2a) Annular sector plate, b) annular plate, c) circular sector plate, d) circular plate

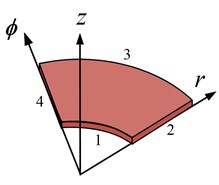
a) $0 \leq ϕ < 2 π$

b) $ϕ = 2 π$

c) $0 \leq ϕ < 2 π$ , $α = 0$

d) $ϕ = 2 π$ , $α = 0$

2.2. Formulation

In the framework of first order shear deformation plate theory, the displacement field in an arbitrary point of a moderately thick annular sector pate is given by:

1

u_{r} (r, ϕ, z, t) = u_{r} (r, ϕ, z) + z θ_{r} (r, ϕ, t),

u_{ϕ} (r, ϕ, z, t) = u_{ϕ} (r, ϕ, z) + z θ_{ϕ} (r, ϕ, t),

w (r, ϕ, z, t) = w_{o} (r, ϕ, t),

where $θ_{r}$ and $θ_{ϕ}$ represents the rotation of transverse normal with respect to $ϕ$ and $r$ directions, $z$ is the thickness coordinate, $u_{r}$ and $u_{ϕ}$ are displacements of the mid plane in $r$ and $ϕ$ directions, respectively, $w_{o}$ is the transverse displacement and $t$ is the time. Thus the corresponding strains at this point are defined in terms of middle surface strains, curvature and twist changes as:

2

ε_{r} = ε_{r}^{o} + z χ_{r}, ε_{ϕ} = ε_{ϕ}^{o} + z χ_{ϕ}, ε_{z} = 0,

γ_{r ϕ} = γ_{r ϕ}^{o} + z χ_{r ϕ}, γ_{r z} = γ_{r z}^{o}, γ_{ϕ z} = γ_{ϕ z}^{o},

where the middle surface strains, curvature and twist changes are written as:

3

ε_{r}^{o} = \frac{\partial u_{r}}{\partial r}, χ_{r} = \frac{\partial θ_{r}}{\partial r},

ε_{ϕ}^{o} = \frac{\partial u_{ϕ}}{r \partial ϕ} + \frac{u_{r}}{r}, χ_{ϕ} = \frac{\partial θ_{ϕ}}{r \partial ϕ} + \frac{θ_{r}}{r},

γ_{r ϕ}^{o} = \frac{\partial u_{ϕ}}{\partial r} + \frac{\partial u_{r}}{r \partial ϕ} - \frac{u_{ϕ}}{r}, χ_{r ϕ} = \frac{\partial θ_{ϕ}}{\partial r} + \frac{\partial θ_{r}}{r \partial ϕ} - \frac{θ_{ϕ}}{r},

γ_{r z}^{o} = \frac{\partial w_{o}}{\partial r} + θ_{r}, γ_{ϕ z}^{o} = \frac{\partial w_{o}}{r \partial ϕ} + θ_{ϕ} .

Assuming the plain stress distribution in accordance with Hooks law, the stress resultants are obtained for Mindlin annular plate by integrating the stresses as shown below:

4

M_{r} = \int_{- h / 2}^{h / 2} σ_{r} z d z = D [\frac{\partial θ_{r}}{\partial r} + \frac{ν}{r} (θ_{r} + \frac{\partial θ_{ϕ}}{\partial ϕ})],

M_{ϕ} = \int_{- h / 2}^{h / 2} σ_{ϕ} z d z = D [\frac{1}{r} (θ_{r} + \frac{\partial θ_{ϕ}}{\partial ϕ}) + ν (\frac{\partial θ_{r}}{\partial r})],

M_{r ϕ} = \int_{- h / 2}^{h / 2} τ_{r ϕ} z d z = D (\frac{1 - ν}{2}) [\frac{1}{r} (\frac{\partial θ_{r}}{\partial ϕ} - θ_{ϕ}) + \frac{\partial θ_{ϕ}}{\partial r}],

Q_{r} = K^{2} \int_{- h / 2}^{h / 2} τ_{r z} d z = K^{2} G h [θ_{r} + \frac{\partial w_{o}}{\partial r}],

Q_{ϕ} = K^{2} \int_{- h / 2}^{h / 2} τ_{ϕ z} d z = K^{2} G h [θ_{ϕ} + \frac{1}{r} \frac{\partial w_{o}}{\partial ϕ}],

where $M_{r}$ , $M_{ϕ}$ and $M_{r ϕ}$ are the bending moments per unit length of the plate, $Q_{r}$ and $Q_{ϕ}$ are the transverse shear forces per unit length of the plate, $σ_{r}$ , $σ_{ϕ}$ are the normal stresses, $τ_{r ϕ}$ , $τ_{r z}$ and $τ_{ϕ z}$ are the shear stresses, $h$ is the plate thickness, $E$ is the modulus of elasticity, $G = E / 2 (1 + ν)$ is the shear modulus, $ν$ is the Poisson ratio, $D = E h^{3} / 12 (1 - ν^{2})$ is the flexural rigidity and $K^{2} = π^{2} / 12$ is the shear correction factor to compensate for the error in assuming the constant shear stress throughout the plate thickness. The equation of motion of the Mindlin annular sector plate is given by:

5

\frac{\partial M_{r}}{\partial r} + \frac{1}{r} \frac{\partial M_{r ϕ}}{\partial ϕ} + \frac{1}{r} (M_{r} - M_{ϕ}) - Q_{r} = \frac{ρ h^{3}}{12} (\frac{\partial^{2} θ_{r}}{\partial t^{2}}),

\frac{\partial M_{r ϕ}}{\partial r} + \frac{1}{r} \frac{\partial M_{ϕ}}{\partial ϕ} + \frac{2}{r} M_{r ϕ} - Q_{ϕ} = \frac{ρ h^{3}}{12} (\frac{\partial^{2} θ_{ϕ}}{\partial t^{2}}),

\frac{\partial Q_{r}}{\partial r} + \frac{1}{r} \frac{\partial Q_{ϕ}}{\partial ϕ} + \frac{Q_{r}}{r} = ρ h \frac{\partial^{2} w_{o}}{\partial t^{2}} .

The boundary conditions for an elastically restrained moderately thick annular sector plate are:

6

k_{a} w_{o} = Q_{r}, K_{a}^{r} θ_{r} = - M_{r}, K_{a}^{t} θ_{ϕ} = - M_{r ϕ}, r = a,

k_{b} w_{o} = - Q_{r}, K_{b}^{r} θ_{r} = M_{r}, K_{b}^{t} θ_{ϕ} = M_{r ϕ}, r = b,

k_{ϕ 0} w_{o} = - Q_{ϕ}, K_{ϕ 0}^{r} θ_{ϕ} = M_{ϕ}, K_{ϕ 0}^{t} θ_{ϕ} = M_{r ϕ}, ϕ = 0,

k_{ϕ 1} w_{o} = Q_{ϕ}, K_{ϕ 1}^{r} θ_{ϕ} = - M_{ϕ}, K_{ϕ 1}^{t} θ_{ϕ} = - M_{r ϕ}, ϕ = α,

where $k_{a}$ , $k_{b}$ ( $k_{ϕ 0}$ and $k_{ϕ 1})$ are translational spring constants, $K_{a}^{r}$ , $K_{b}^{r}$ ( $K_{ϕ 0}^{r}$ and $K_{ϕ 1}^{r})$ are rotational spring constants attached in radial direction and $K_{a}^{t}$ , $K_{b}^{t}$ ( $K_{ϕ 0}^{t}$ and $K_{ϕ 1}^{t})$ are rotational spring constants attached in circumferential direction at $r = a$ and $b$ ( $ϕ = 0$ and $ϕ = α)$ respectively. All the classical homogeneous boundary conditions can be simply considered as special cases when the spring constants are either extremely large or substantially small. For instance, a clamped boundary (C) is achieved by simply setting the stiffness of the entire springs equal to infinity (which is represented by a very large number, 10¹⁴). Inversely, a free boundary (F) is gained by setting the stiffness of the entire springs equal to zero. The units for the translational and rotational springs are N/m and Nm/rad, respectively.

2.3. Trigonometric series representation for the displacement functions

Regardless of the plate shape and type of boundary conditions, the displacement and rotation functions are invariably expressed in the form of simple trigonometric series expansion as:

7

θ_{r (r, ϕ)} = \sum_{m = n = - 2}^{\infty} A_{m n} φ_{m} (r) φ_{n} (ϕ),

θ_{ϕ (r, ϕ)} = \sum_{m = n = - 2}^{\infty} B_{m n} φ_{m} (r) φ_{n} (ϕ),

w_{o (r, ϕ)} = \sum_{m = n = - 2}^{\infty} C_{m n} φ_{m} (r) φ_{n} (ϕ),

where $A_{m n}$ , $B_{m n}$ , $C_{m n}$ denotes the expansion coefficients and:

φ_{m} (r) = \{\begin{array}{l} c o s λ_{m} (r), m \geq 0, \\ s i n λ_{m} (r), m < 0, \end{array} φ_{n} (ϕ) = \{\begin{array}{l} c o s λ_{n} (ϕ), n \geq 0, \\ s i n λ_{n} (ϕ), n < 0, \end{array} λ_{m} = \frac{m π}{R}, λ_{n} = \frac{n π}{α} .

A solution can be obtained either in strong form by letting the series satisfy the relevant equations exactly on a point-wise basis, or in weak form by solving the series coefficients approximately using, for instance, the Rayleigh-Ritz technique. The weak form of solution will be sought here since it will be more attractive in modeling complex structures. To employ this method for this analysis, it is necessary to state the potential and kinetic energy in terms of displacement fields. The total potential energy of the spring restrained plate which is composed of two parts, namely, the strain energy of the Mindlin annular sector plate is given by:

8

U_{p l a t e} = \frac{1}{2} \int_{0}^{α} \int_{a}^{b} [\begin{array}{l} D [\begin{matrix} {(\frac{\partial θ_{r}}{\partial r})}^{2} + \frac{2 ν}{r} \frac{\partial θ_{r}}{\partial r} (\frac{\partial θ_{ϕ}}{\partial ϕ} + θ_{r}) + \frac{1}{r^{2}} {(\frac{\partial θ_{ϕ}}{\partial ϕ} + θ_{r})}^{2} \\ + (\frac{1 - ν}{2}) \frac{1}{r^{2}} {(θ_{ϕ} - \frac{r \partial θ_{ϕ}}{\partial r} - \frac{\partial θ_{r}}{\partial ϕ})}^{2} \end{matrix}] \\ + K^{2} G h [{(\frac{\partial w_{o}}{\partial r} + θ_{r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial w_{o}}{\partial ϕ} + r θ_{ϕ})}^{2}] \end{array}] r d r d ϕ,

and the potential energy stored in the boundary springs, can be expressed as:

9

U_{b s} = \frac{1}{2} [\begin{array}{l} (\int_{0}^{α} [a {[k_{a} w_{o}^{2} + K_{a}^{r} {θ_{r}}^{2} + K_{a}^{t} {θ_{ϕ}}^{2}]}_{_{_{r = a}}} + b {[k_{b} w_{o}^{2} + K_{b}^{r} {θ_{r}}^{2} + K_{b}^{t} {θ_{ϕ}}^{2}]}_{r = b}] d ϕ) \\ + (\int_{a}^{b} [{[k_{a} w_{o}^{2} + K_{ϕ 0}^{r} {θ_{r}}^{2} + K_{ϕ 0}^{t} {θ_{ϕ}}^{2}]}_{ϕ = 0} + {[k_{b} w_{o}^{2} + K_{ϕ 1}^{r} {θ_{r}}^{2} + K_{ϕ 1}^{t} {θ_{ϕ}}^{2}]}_{ϕ = α}]) r d r \end{array}] .

The kinetic energy expression for annular sector plate is expressed as:

10

T_{p} = \frac{1}{2} ω^{2} \int_{0}^{α} \int_{a}^{b} (ρ h {w_{o}}^{2} + \frac{ρ h^{3}}{12} ({θ_{r}}^{2} + {θ_{ϕ}}^{2})) r d r d ϕ .

As mentioned above, an annular plate can be mathematically viewed as a special case when the sector angle of an annular sector plate is set equal to 2 $π$ . However, this transition of annular sector plate into annular plate is not possible with this simple mathematical operation because the continuity of the displacement and its derivatives at this simple mathematical operation alone cannot automatically ensure a complete transition of the sector into an annular plate that is, the continuities of the displacements and their derivatives at $ϕ = 0$ and $ϕ = 2 π$ . To overcome this problem, a set of coupling springs will be used to enforce the continuity conditions for the displacements at the edges $ϕ = 0$ and $ϕ = 2 π$ . The potential energy stored in these coupling springs will be given by:

11

U_{C S} = \frac{1}{2} \int_{a}^{b} [\begin{matrix} k_{c s} {({w_{o}|}_{ϕ = 0} - {w_{o}|}_{ϕ = 2 π})}^{2} + K_{c s}^{r} {({θ_{r}|}_{ϕ = 0} - {θ_{r}|}_{ϕ = 2 π})}^{2} \\ + K_{c s}^{t} {({θ_{ϕ}|}_{ϕ = 0} - {θ_{ϕ}|}_{ϕ = 2 π})}^{2} \end{matrix}] d r,

where $k_{c s}$ , $K_{c s}^{r}$ and $K_{c s}^{t}$ are the stiffnesses for translational coupling spring, rotational coupling springs in radial direction and rotational coupling springs in tangential direction respectively.

The Lagrangian for the annular sector plate can be generally expressed as:

12

L = U_{p l a t e} + U_{b s} + U_{c s} - T_{p} .

Substituting Eqs. (9-11) in (12) and minimizing Lagrangian against all the unknown series expansion coefficients we can obtain a series of linear algebraic expressions in a matrix form as:

13

(K - ω^{2} M) E = 0,

where $E$ is a vector which contains all the unknown series expansion coefficients that is:

14

E = {\{\begin{array}{l} A_{- 2, - 2}, A_{- 2, - 1}, A_{- 2,0}, . . ., A_{m', - 2}, A_{m', - 1,}, A_{m', 0} . . ., A_{m', n'}, . . ., A_{M, N} \\ B_{- 2, - 2}, B_{- 2, - 1}, B_{- 2,0}, . . ., B_{m', - 2}, B_{m', - 1}, B_{m', 0}, . . ., B_{m', n'}, . . ., B_{M, N} \\ C_{- 2, - 2}, C_{- 2, - 1}, C_{- 2,0}, . . ., C_{m', - 2}, C_{m', - 1}, C_{m', 0}, . . ., C_{m', n'}, . . ., C_{M, N} \end{array}\}}^{T} .

And $K$ and $M$ are the stiffness and mass matrices, respectively. For conciseness, the detailed expressions for the stiffness and mass matrices are not shown here. The eigenvalues (or natural frequencies) and eigenvectors of moderately thick annular sector plates can now be easily and directly determined from solving a standard matrix eigenvalue problem Eq. (13). For a given natural frequency, the corresponding eigenvector actually contains the series expansion coefficients which can be used to construct the physical mode shape based on Eqs. (7).

3. Results and discussion

In order to verify the convergence, accuracy, reliability and applicability of the present method for moderately thick annular, circular plates and their sector counter parts, several numerical examples are presented here along with the reference results from literature and ABAQUS. First of all the convergence of the present method is studied. Using different truncation terms ( $M = N =$ 2, 4, 6, 8, 10, 12, 14) several sets of results are obtained for fully clamped Mindlin annular sector plate having different sector angles and presented in Table 1 and 2 as shown.

Table 1First five non-dimensional frequency parameter for fully clamped Mindlin annular sector plate having a/b= 0.6, h/b= 0.1

Sector angle Ø	$M = N$	Non dimensional frequency parameter $Ω = ω b^{2} {(ρ h / D)}^{1 / 2}$
		Mode sequence
		1	2	3	4	5
	2	145.584	240.451	251.723	331.721	391.843
	4	144.104	237.420	249.040	328.660	350.364
	6	144.032	237.301	248.941	328.487	349.816
$π$ /6	8	144.020	237.280	248.924	328.452	349.739
	10	144.017	237.274	248.920	328.442	349.720
	12	144.016	237.272	248.918	328.438	349.713
	14	144.015	237.271	248.917	328.436	349.711
	ABAQUS	144.534	238.503	250.295	329.634	350.523

Table 2First five non-dimensional frequency parameter for CCCC Mindlin annular sector plate having a/b= 0.6, h/b= 0.1

Sector angle Ø	$M = N$	Non Dimensional frequency parameter $Ω = ω b^{2} {(ρ h / D)}^{1 / 2}$
		Mode sequence
		1	2	3	4	5
	2	104.250	116.563	163.387	223.325	232.424
$π$ /2	4	102.977	112.649	130.467	173.504	220.564
	6	102.911	112.460	129.978	155.396	187.319
	8	102.900	112.420	129.896	154.985	185.972
	10	102.897	112.408	129.871	154.895	185.781
	12	102.896	112.403	129.862	154.865	185.726
	14	102.895	112.401	129.857	154.852	185.705
	ABAQUS	103.271	112.776	130.262	155.343	182.096

A fast convergence can be observed in the tabulated results for different truncation numbers and also a good agreement can be observed between the present values and the ABAQUS results. Similarly figure 3 shows convergence pattern for the 1st, 3rd, 5th and 8th mode for a moderately thick circular sector plate having clamped circular edge and simply supported radial edges.

Fig. 3Convergence pattern for frequency parameters with no. of truncation terms

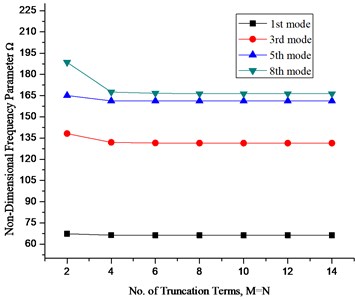
It can be seen that the results converge very quickly even with small number of truncation terms. Thus a suitable truncation number should be used to achieve the accuracy of the largest desired frequency. In view of above and excellent convergence behavior of the current solution, the truncation number for subsequent calculation in the present method is taken as $M = N =$ 12.

After verifying the fast convergence of the preset method, results for Mindlin annular and circular plates and their sector counterparts are obtained and tabulated for various sector angles and different boundary conditions along with the reference results from literature. Table 3 shows fundamental frequency parameters for Mindlin annular sector plates having different sector angles and thickness to radius ratio. The plate has simply supported radial edges and different boundary conditions at the circular edges. The results have been compared with ABAQUS software as well as those available in literature.

Table 3Fundamental frequency parameter Ω=ωb2ρh/D1/2 for Mindlin annular sector plates having SS radial edges and various boundary conditions at the inner and outer circumferential edges (a/b= 0.5)

Sector angle Ø	$h / b$	Method	Boundary conditions
Sector angle Ø	$h / b$	Method	S-S	S-F	F-S	F-C
195	0.1	Present	38.365	4.560	10.224	19.998
		Ref [12]	38.636	4.675	10.227	19.999
		ABAQUS	38.580	4.540	11.159	20.923
	0.2	Present	32.508	4.005	9.130	17.503
		Ref [12]	32.871	4.542	9.366	17.582
		ABAQUS	32.676	4.067	10.014	18.239
210	0.1	Present	38.222	4.507	9.685	19.620
		Ref [12]	38.455	4.584	9.664	19.610
		ABAQUS	38.223	4.230	9.479	19.516
	0.2	Present	32.419	3.997	8.681	17.235
		Ref [12]	32.734	4.458	8.877	17.294
		ABAQUS	32.469	3.923	8.590	17.201
270	0.1	Present	37.868	4.392	8.213	18.654
		Ref [12]	38.010	4.372	8.130	18.622
		ABAQUS	37.875	4.197	8.015	18.574
	0.2	Present	32.200	3.999	7.450	16.548
		Ref [12]	32.394	4.263	7.546	16.566
		ABAQUS	32.252	3.932	7.366	16.524

Next we verify the applicability of this unified method for annular plates. As mentioned previously an annular plate can be viewed as a special case of annular sector plate if the sector angle becomes equal to 2 $π$ . Results for Mindlin annular plate for different combination of classical boundary conditions at the inner and outer edges for various cutout ratios are also calculated and presented in Table 4 along with those obtained from ABAQUS. A very close agreement can be observed in the calculated results. This close agreement verifies the applicability of the coupling spring technique for calculating frequency parameters for a complete annular plate without modifying the solution procedure.

Table 4Non dimensional frequency parameter Ω=ωb2ρh/D1/2 for Mindlin annular plates with various cutout ratio and boundary conditions (h/b= 0.2)

B.C	$a / b$	Method	Mode sequence
B.C	$a / b$	Method	1	2	3	4	5
SC	0.2	Present	21.161	22.228	22.228	27.545	27.550
	0.2	ABAQUS	21.200	22.271	22.272	27.596	27.596
	0.4	Present	32.154	32.829	32.829	35.411	35.414
	0.4	ABAQUS	32.243	32.920	32.920	35.511	35.511
	0.6	Present	56.120	56.458	56.458	57.642	57.643
	0.6	ABAQUS	56.357	56.697	56.697	57.885	57.887
SF	0.2	Present	2.082	2.082	3.225	4.980	4.998
	0.2	ABAQUS	2.084	2.084	3.224	4.975	4.975
	0.4	Present	3.280	3.280	3.581	5.464	5.471
	0.4	ABAQUS	3.282	3.282	3.578	5.465	5.465
	0.6	Present	4.703	5.089	5.089	7.402	7.407
	0.6	ABAQUS	4.699	5.090	5.090	7.411	7.411
FC	0.2	Present	9.476	16.774	16.774	26.240	26.247
	0.2	ABAQUS	9.481	16.797	16.797	26.288	26.289
	0.4	Present	12.156	15.995	15.995	24.240	24.246
	0.4	ABAQUS	12.163	16.014	16.014	24.248	24.284
	0.6	Present	21.219	22.812	22.812	27.275	27.278
	0.6	ABAQUS	21.244	22.844	22.844	27.324	27.325
CF	0.2	Present	4.191	4.191	4.809	5.750	5.756
	0.2	ABAQUS	4.193	4.193	4.810	5.746	5.748
	0.4	Present	8.017	8.017	8.175	8.865	8.868
	0.4	ABAQUS	8.022	8.022	8.179	8.870	8.870
	0.6	Present	17.148	17.198	17.198	17.802	17.803
	0.6	ABAQUS	17.168	17.220	17.220	17.826	17.826
CC	0.2	Present	24.346	25.313	25.313	29.515	29.519
	0.2	ABAQUS	24.413	25.380	25.380	29.583	29.584
	0.4	Present	37.641	38.196	38.196	40.238	40.240
	0.4	ABAQUS	37.784	38.339	38.339	40.382	40.383
	0.6	Present	64.159	64.462	64.462	65.485	65.486
	0.6	ABAQUS	64.496	64.799	64.800	65.821	65.823

As mentioned earlier when the inner radius of an annular sector plate is approximated to a very small number say $a =$ 0.00001, then the annular sector plate converges to circular sector plate. The same method has been applied to circular sector plates and results for circular sector plates having different sector angles and boundary conditions at the radial and circumferential edges It should be noted that the symbol S stands for simply supported, C stands for clamped and F stand for free boundary conditions. The edges are taken in the counter clock wise direction, so SCS boundary conditions means simply supported radial edges and clamped circumferential edge. First three non-dimensional frequency parameters are calculated and presented in the Table 5 along with the reference results. It can be observed that the frequency parameters are in close agreement with the reference data.

Next we calculate the frequency parameter for various boundary conditions for a complete Mindlin circular plate having different thickness to radius ratio. In order to achieve this two simple modification needs to be done in the solution algorithm. First is equating the inner radius equal to a very small number say $a =$ 0.00001 and second is equating the sector angle equal to 2 $π$ Table 6 presents first five non dimensional frequency parameter for a complete circular plate subjected to different boundary conditions at the circumferential edge and having different thickness to radius ratio. It should be noted that for the ‘F’; free boundary condition; the zero frequency parameters for the first six rigid body modes have not been taken into account in the Table 6. It can be observed that the frequency parameter decreases with increasing thickness to radius ratio in all the three types of boundary conditions listed. A good agreement between the presented results and those obtained through ABAQUS can also be observed which proves the applicability of the present method for calculating the frequency parameters for Mindlin circular plates also.

Table 5First three non-dimensional frequency parameters Ω=ωb2ρh/D1/2 for circular sector plates having different combination of classical boundary conditions and sector angle (h/b= 0.2, a/b= 0.00001)

Sector angle Ø	BC	Mode sequence	Present	Ref. [13]	ABAQUS
30	SCS	1	66.256	67.933	66.490
		2	98.936	102.560	99.373
		3	131.364	132.860	132.146
90	SSS	1	21.006	21.977	21.030
		2	41.254	42.699	41.339
		3	48.863	50.307	48.981
120	CCC	1	27.311	27.314	27.372
		2	40.977	40.983	41.105
		3	52.324	52.338	52.515

Table 6First five non-dimensional frequency parameter Ω=ωb2ρh/D1/2 for a Mindlin circular plate having different boundary conditions and thickness to radius ratio (a/b= 0.00001)

B.C	$h / b$	Method	Mode Sequence
B.C	$h / b$	Method	1	2	3	4	5
C	0.1	Present	9.941	20.178	20.178	32.210	32.223
	0.1	ABAQUS	9.939	20.176	20.176	32.220	32.222
	0.2	Present	9.240	17.758	17.758	26.994	27.000
	0.2	ABAQUS	9.246	17.782	17.782	27.044	27.045
	0.25	Present	8.807	16.446	16.446	24.478	24.482
	0.25	ABAQUS	8.816	16.479	16.479	24.540	24.540
S	0.1	Present	4.895	13.512	13.512	24.324	24.336
	0.1	ABAQUS	4.892	13.508	13.508	24.315	24.317
	0.2	Present	4.777	12.620	12.620	21.690	21.696
	0.2	ABAQUS	4.776	12.625	12.625	21.710	21.710
	0.25	Present	4.696	12.080	12.080	20.272	20.276
	0.25	ABAQUS	4.696	12.089	12.089	20.300	20.300
F	0.1	Present	5.283	5.299	8.869	12.153	12.248
	0.1	ABAQUS	5.275	5.275	8.865	12.062	12.062
	0.2	Present	5.117	5.125	8.505	11.366	11.428
	0.2	ABAQUS	5.113	5.113	8.504	11.316	11.316
	0.25	Present	5.011	5.018	8.268	10.910	10.960
	0.25	ABAQUS	5.009	5.009	8.268	10.871	10.871

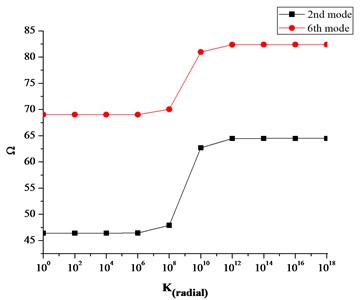
All the results tabulated so far have been calculated for various combinations of classical boundary conditions which are treated as a special case of elastic boundary conditions in which the stiffness values for the restraining springs are set either equal to a very high value i.e. 10¹⁴ or a very low number zero. It is therefore necessary to study the effect of these restraining spring stiffnesses on the frequency characteristics for these plates. Figs. 4-6 shows the effect of boundary restraining springs on the frequency parameter ‘ $Ω$ ’ for a fully clamped annular plate having $a / b =$ 0.6 and $h / b =$ 0.2.

Fig. 4 shows effect of translational spring stiffness on the second and sixth mode frequency parameter of annular plate in which the stiffness of the translational spring stiffness varies from 0 to 1e14 while the stiffnesses of the rotational spring in radial and tangential direction ( ) are kept constant i.e. 1e14.

Similarly, Figs. 5 and 6 have been obtained by assigning the corresponding boundary spring stiffness, a value ranging from 0 to 10¹⁴ and keeping the stiffnesses of other sets of spring equal to 10¹⁴.

Fig. 4Effect of translational spring stiffness k on frequency parameter Ω

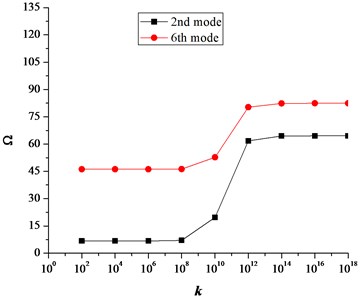
Fig. 5Effect of rotational spring stiffness K attached in tangential direction on Ω

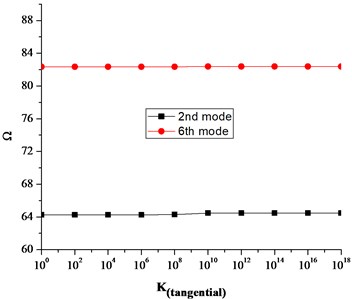
Fig. 6Effect of rotational spring stiffness K attached in radial direction on Ω

Similarly, Fig. 7(a)-(c) shows the effect of coupling springs on the frequency parameter $Ω$ .

It can be seen that the translational and rotational boundary springs sufficiently affect the frequency parameters. More precisely the translational boundary restraining spring tend to be more influential when its stiffness varies from 10⁸ to 10¹³. Similarly, the influential range for the rotational boundary spring in the radial direction is 10⁶ to 10¹². However, the influence of rotational boundary spring in the tangential direction is very small as seen in Fig. 5. Also it can be seen in Fig. 7(a)-(c) that influential range for the coupling springs is much smaller as compared to the boundary restraining springs. This influential range is the elastic range and frequency parameters can easily be calculated for elastic boundary conditions by assigning the proper stiffness values to the boundary restraining springs without modifying the solution procedure or algorithms.

We know that in practical engineering, designing or development of any mechanical system or a product, structure vibration analysis and testing is an important part to assess the real behavior of the structure when subjected to static or dynamic loads. In other words, to better understand any structural vibration problem, the resonant frequencies of a structure need to be identified and quantified in order to avoid well known resonance phenomena which can result in catastrophe. Today, modal analysis has become a widespread means of finding the modes of vibration of a machine or a structure.

Fig. 7Effect of coupling springs on the frequency parameter Ω

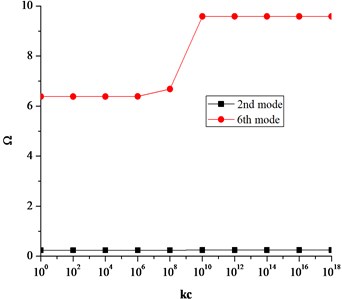
a) Effect of translational coupling spring $k c$ on frequency parameter $Ω$

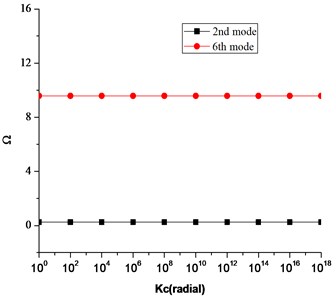
b) Effect of rotational coupling spring in radial direction $K c$ on frequency parameter $Ω$

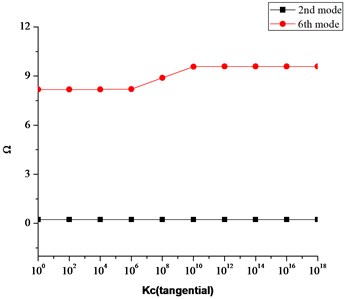
c) Effect of rotational coupling spring in tangential direction $K c$ on frequency parameter $Ω$

Various analytical methods have been developed over the years to accurately estimate the resonant frequencies or modes of vibrations of any structure when subjected to different boundary conditions. Once these frequencies are calculated they are used to estimate the modes of vibrations of a structure which are determined by the material properties and boundary conditions. Each mode of vibration is defined by a natural (modal or resonant) frequency, modal damping, and a mode shape. If there is a slight change in material properties or boundary conditions of a structure, its modes of vibration will also change. Therefore, it is important to estimate these frequencies for any change in material properties as well as boundary conditions because in practical engineering applications, the material properties of a structure and boundary conditions may vary. Furthermore, most of the existing techniques available so far to estimate these natural or resonant frequencies are limited to classical boundary conditions (clamped, free, simply supported etc.), however in practical engineering applications the structures are not always subjected to classical boundary conditions rather they may be subjected to elastic boundary conditions.

In the present manuscript, the unified method presented not only helps to accurately estimate these natural frequencies of circular and annular plates and their sector counter parts when they are subjected to classical boundary conditions but also when they are subjected to general elastic boundary conditions. The presented results give an insight of the modes of vibration of these plates having different material properties and subjected to elastic boundary conditions. Moreover, another important contribution of this technique is that this method does not require any changes in procedure or solution algorithms to accommodate different geometries, material properties or boundary conditions. The same solution algorithm or procedure can be used to estimate natural frequencies for different materials and boundary conditions. Different boundary conditions (classical, elastic, uniform & non-uniform) can easily be achieved by simply changing the stiffnesses of the translational and rotational springs attached at the boundaries or edges of these plates”.

4. Conclusion

In this paper a unified method is presented for vibration analysis of Mindlin annular, circular and their sector counter parts with arbitrary boundary conditions at their edges. Coupling springs technique has been utilized to avoid inconvenient formulation or procedural modification to accommodate different boundary conditions and geometrical shapes of the plates. Irrespective of the shape of the plate and the type of boundary conditions, each of the displacement function is expressed as a new form of trigonometric expansion with high convergence rate. Rayleigh-Ritz method has been used to determine the expansion coefficients. The current method therefore can be universally applied to a wide range of vibration problems involving different shapes, boundary conditions, varying materials and geometric properties without modifying the solution algorithms and procedure. The unification, fast convergence, accuracy and reliability have been fully demonstrated through several numerical examples involving different shapes and boundary conditions. Furthermore, the effect of boundary restraining springs and coupling springs on the frequency parameter have also been studied.

References

Deresiewicz H., Mindlin R. D. Axially symmetric flexural vibrations of a circular disk. American Society of Mechanical Engineers Journal of Applied Mechanics, Vol. 22, 1955, p. 86-88.

Publisher
Soni S. R., Amba Rao C. L. On radially symmetric vibrations of orthotropic non uniform disks including shear deformation. Journal of Sound and Vibration, Vol. 42, 1975, p. 57-63.

Publisher
Gupta U. S., Lal R. Axisymmetric vibrations of polar orthotropic Mindlin annular plates of variable thickness. Journal of Sound and Vibration, Vol. 98, 1985, p. 565-573.

Publisher
Cheung Y. K., Kwok W. L. Dynamic analysis of circular and sector thick layered plates. Journal of Sound and Vibration, Vol. 42, 1975, p. 147-158.

Publisher
Cheung M. S., Chan M. Y. T. Static and dynamic analysis of thin and thick sectorial plates by the finite strip method. Computers and Structures, Vol. 14, 1981, p. 79-88.

Publisher
Xiang Y., Liew K. M., Kitipornchai S. On transverse vibration of thick annular sector plates. Transactions of the American Society of Civil Engineers, Journal of Engineering Mechanics, Vol. 119, Issue 8, 1993, p. 1579-1599.

Publisher
Liew K. M., Kitipornchai S., Xiang Y. Vibration of annular sector Mindlin plates with internal radial line and circumferential arc supports. Journal of Sound and Vibration, Vol. 183, Issues 3-8, 1995, p. 401-419.

Publisher
Xiang Y., Liew K. M., Kitipornchai S. Vibrations of circular and annular Mindlin plates with internal ring stiffeners. Journal of Acoustical Society of America, Vol. 100, Issue 6, 1996, p. 3696-3705.

Publisher
Kitipornchai S., Xiang Y., Liew K. M. Vibration analysis of corner supported Mindlin plates of arbitrary shape using the Lagrange multiplier method. Journal of Sound and Vibration, Vol. 173, Issue 4, 1994, p. 457-470.

Publisher
Bani Singh, Saleh Hassan M. Transverse vibration of a circular plate with arbitrary thickness variation. International Journal of Mechanical Science, Vol. 40, Issue 11, 1998, p. 1089-1104.

Publisher
Xiang Y., Zhang L. Free vibration analysis of stepped circular Mindlin plates. Journal of Sound and Vibration, Vol. 280, 2005, p. 633-655.

Publisher
Mcgee O. G., Huang C. S., Leissa A. W. Comprehensive exact solutions for free vibrations of thick annular sectorial plates with simply supported radial edges. International Journal of Mechanical Sciences, Vol. 37, Issue 5, 1995, p. 537-566.

Publisher
Liu F. L., Liew K. M. Free vibration analysis of Mindlin sector plates: numerical solutions by differential quadrature methods. Computer Methods in Applied Mechanics and Engineering, Vol. 177, 1999, p. 77-92.

Publisher
Liew K. M., Liu F. L. Differential quadrature method for free vibrations of shear deformable annular sector plates. Journal of Sound and Vibration, Vol. 230, Issue 2, 2000, p. 335-356.

Publisher
Wu T. Y., Liu G. R. Free vibration analysis of circular plates with variable thickness by the generalized differential quadrature rule. International Journal of Solid and Structures, Vol. 38, 2001, p. 7967-7980.

Publisher
Huang C. S., Ho K. H. An analytical solution for vibrations of polarly orthotropic Mindlin sectorial plate with simply supported radial edges. Journal of Sound and Vibration, Vol. 273, 2004, p. 277-294.

Publisher
Jae Hoon Kang Three-dimensional vibration analysis of thick circular and annular plates with non-linear thickness variation. Computers and Structures, Vol. 81, 2003, p. 1663-1675.

Publisher
So J., Leissa A. W. Three dimensional vibrations of thick circular and annular plates. Journal of Sound and Vibration, Vol. 209, 1998, p. 15-41.

Publisher
Zhou D., Au F. T. K., Cheung Y. K., Lo S. H. Three-dimensional vibration analyses of circular and annular plates via the Chebyshev-Ritz method. International Journal of Solid and Structures, Vol. 40, 2003, p. 3089-3105.

Publisher
Zhou D., Lo S. H., Cheung Y. K. 3-D vibration analysis of annular sector plates using the Chebyshev-Ritz method. Journal of Sound and Vibration, Vol. 320, 2009, p. 421-437.

Publisher
Hashemi S. H., Tahir H. R. D., Omidi M. 3-D free vibration analysis of annular plates on Pasternak elastic foundation via p-Ritz method. Journal of Sound and Vibration, Vol. 311, 2008, p. 1114-1140.

Publisher
Civalek Omer, Gurses Murat Free vibration of annular Mindlin plates with free inner edge via discrete singular convolution method. The Arabian Journal for Science and Engineering, Vol. 34, Issue 1, 2009, p. 81-90.

Search CrossRef
Civalek Omer, Ersoy Haken Free vibration and bending analysis of circular Mindlin plates using singular convolution method. Communications in Numerical Methods in Engineering, Vol. 25, 2009, p. 907-922.

Publisher
Jomehzadeh E., Saidi A. R. Analytical solution for the free vibration of transversely isotropic sector plates using a boundary layer function. Thin Walled Structures, Vol. 47, 2009, p. 82-88.

Publisher
Jomehzadeh E., Saidi A. R. Accurate natural frequencies of transversely isotropic moderately thick annular sector plates. Journal of Mechanical Engineering Science, Vol. 223, Issue 2, 2009, p. 307-317.

Publisher
Bashmal S., Bhat R., Rakheja S. Frequency equations for the in-plane vibration of circular annular disks. Advances in Acoustic and Vibrations, Vol. 2010, 2010.

Publisher
Bashmal S., Bhat R., Rakheja S. In-plane free vibration analysis of an annular disk with point elastic support. Journal of Shock and Vibration, Vol. 18, 2011, p. 627-640.

Publisher
Karamooz Ravari M. R., Forouzan M. R. Frequency equations for the in-plane vibration of orthotropic circular annular plates. Archives of Applied Mechanics, Vol. 81, 2010, p. 1307-1322.

Publisher
Sari M. S., Butcher E. A. Free vibration analysis of rectangular and annular Mindlin plates with undamaged and damaged boundaries by the spectral collocation method. Journal of Vibration and Control, 2011, p. 1-15.

Publisher
Bisadi H., Es’haghi M., Rokni H., Ilkhani M. Benchmark solution for transverse vibration of annular Reddy plates. International Journal of Mechanical Sciences, Vol. 56, 2012, p. 35-49.

Publisher
Mehdi Es’Haghi Accurate approach implementation in vibration analysis of thick sector plates. International Journal of Mechanical Sciences B, Vol. 79, 2014, p. 1-14.

Publisher
Shi Dongyan, Shi Xianjie, Li Wen, Wang Qingshan Dynamic analysis of annular sector plates with general boundary supports. Structural Acoustics and Vibrations ICA, Montreal, Canada, Vol. 19, 2013.

Publisher
Shi Xianjie, Shi Dongyan, Qin Zhengrong, Wang Qingshan In-plane vibration analysis of annular plates with arbitrary boundary conditions. The Scientific World Journal, Vol. 2014, 2014.

Publisher
Shi Xianjie, Shi Dongyan, Li Wen L., Wang Qingshan A unified method for free vibration of circular, annular and sector plates with arbitrary boundary conditions. Journal of Vibration and Control, 2014.

Publisher

Cited by

Symmetric and asymmetric vibrations of rotating GPLRC annular plate

Yukang Yang | Ji-an Li | Bo Chen | Youheng Dong | Yinghui Li

(2023)

About this article

Received

14 January 2016

Accepted

17 August 2016

Published

31 December 2016

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2016.16834

Keywords

vibrations

circular plates

annular plates

sector plates

natural frequency

mode shapes

arbitrary boundary conditions

Acknowledgements

The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (No. U1430236) and Natural Science Foundation of Heilongjiang Province of China (No. E2016024)

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 11 28

Free vibration of circular annular plate with different boundary conditions

Yash Jaiman, Baij Singh

Research article

2019 11 28

Comparative study for modal analysis of circular plates with various cutouts and end conditions

Vedanth Bhatnagar, Pavan Kishore Mamaduri, Sreenivasulu B

Research article

2019 03 15

Free vibrational characteristics determination of plates with various cutouts

M. L. Pavan Kishore, Ch. Rajesh, Ram Komawar

Research article

2017 09 30

Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments

Qing-Lu Li, Wei-Di Luan, Zuo-Quan Zhu

F.  Ahad, D. Shi, A. U. Rehman, and H. M. Waqas, “A Unified method for vibration analysis of moderately thick annular, circular plates and their sector counterparts subjected to arbitrary boundary conditions,” Journal of Vibroengineering, Vol. 18, No. 8, pp. 5048–5062, Dec. 2016, https://doi.org/10.21595/jve.2016.16834

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16834
UR  - https://doi.org/10.21595/jve.2016.16834
TI  - A Unified method for vibration analysis of moderately thick annular, circular plates and their sector counterparts subjected to arbitrary boundary conditions
T2  - Journal of Vibroengineering
AU  - Ahad, Fazl e
AU  - Shi, Dongyan
AU  - Rehman, Anees Ur
AU  - Waqas, Hafiz M.
PY  - 2016
DA  - 2016/12/31
PB  - JVE International Ltd.
SP  - 5048-5062
IS  - 8
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Ahad_2016,
	doi = {10.21595/jve.2016.16834},
	url = {https://doi.org/10.21595/jve.2016.16834},
	year = 2016,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {8},
	pages = {5048--5062},
	author = {Fazl e Ahad and Dongyan Shi and Anees Ur Rehman and Hafiz M. Waqas},
	title = {A Unified method for vibration analysis of moderately thick annular, circular plates and their sector counterparts subjected to arbitrary boundary conditions},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]F. e Ahad, D. Shi, A. U. Rehman, and H. M. Waqas, “A Unified method for vibration analysis of moderately thick annular, circular plates and their sector counterparts subjected to arbitrary boundary conditions,” Journal of Vibroengineering, vol. 18, no. 8, pp. 5048–5062, Dec. 2016, doi: 10.21595/jve.2016.16834.

Copy IEEE

Copied to clipboard!

Ahad, Fazl e, Dongyan Shi, Anees Ur Rehman, and Hafiz M. Waqas. “A Unified Method for Vibration Analysis of Moderately Thick Annular, Circular Plates and Their Sector Counterparts Subjected to Arbitrary Boundary Conditions.” Journal of Vibroengineering 18, no. 8 (December 31, 2016): 5048–62. https://doi.org/10.21595/jve.2016.16834.

Copy Chicago

Copied to clipboard!

A Unified method for vibration analysis of moderately thick annular, circular plates and their sector counterparts subjected to arbitrary boundary conditions

Abstract

1. Introduction

2. Theoretical formulation

2.1. Description of the model

2.2. Formulation

2.3. Trigonometric series representation for the displacement functions

3. Results and discussion

4. Conclusion

References

Cited by

About this article

Related Articles