Modal characterization of rotors by unbalance response

Cruz, Pedro; Gutiérrez, Enrique; Szwedowicz, Dariusz; Figueroa, Rafael; Morales, Josefa

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2016

Check for updates

Modal characterization of rotors by unbalance response

Pedro Cruz¹

Enrique Gutiérrez²

Dariusz Szwedowicz³

Rafael Figueroa⁴

Josefa Morales⁵

^{1, 5}The Autonomous University of San Luis Potosí, SLP, Mexico

^{2, 3}National Center for Research and Technological Development Research, Cuernavaca, Mexico

⁴The Sonora Institute of Technology, Sonora, Mexico

Corresponding Author:

Pedro Cruz

Cite the article Download PDF

Downloads 1425

Abstract

A method for determining the complete modal model of rotors affected by gyroscopic moments is proposed. Unlike the case of conventional dynamic systems, the models of these rotors consist of three sets of parameters: the eigenvalues, or complex natural frequencies; the right eigenvalues, or modal forms; and the left eigenvectors. The proposed method has an advantage over existing methods in that it is based on the response analysis of the unbalanced rotor, and therefore does not require the use of special excitation devices nor mounting or dismounting the rotor in order to carry out the tests. It has been proven that although this method does not permit a complete description of the rotor dynamic at each rotational speed to be obtained, its modal parameters can be calculated via the synchronous component (1X) of the response related to the unbalance. The application of the proposed method is shown with an illustrative example based on the finite elements model of a rotor.

1. Introduction

When a structure has the ability to rotate, the movements of rotation and vibration interact with each other, creating forces that are not present in the stationary state. These forces and moments produce changes in the dynamic properties of the structures and in the response to the excitation forces to which they are subjected. When a body rotates, it is exposed to forces that depend on its rotational velocity, as is the case with inertial forces (Coriolis forces and gyroscopes). Gyroscopic forces, which also depend on the linear velocity of the rotor, are of special interest, as they lead to the loss of reciprocity in the movement equations of rotary structures [1]. These forces are represented via an asymmetrical component in the damping matrix. Maxwell’s reciprocity principle, which is the basis of the conventional dynamic characterization methods, and in particular of modal characterization, is not applicable to this type of system. Due to this loss of reciprocity, the dynamic characterization of gyroscopic systems requires a greater number of tests than conventional systems. In addition, it is necessary to identify a greater number of parameters than in systems with symmetrical matrices. Therefore, in order to characterize a non-gyroscopic system, it is sufficient to measure its response to a force applied to only one degree of freedom (DOF). For gyroscopic systems, it is necessary to apply forces to several DOFs in successive tests. This is because, due to the loss of reciprocity, it is not valid to suppose that the response in DOF A caused by a force applied in B is equal to the response in B caused by a force applied in A; both tests must be carried out, and this approximately duplicates the quantity of tests required. One of the main limitations of modal tests for characterization of gyroscopic systems is the difficulty faced when attempting to apply controlled excitation forces to the rotary elements. Although techniques have been developed for this, they are difficult to apply and to a certain degree are only applicable to controlled conditions, such as those found in a laboratory [2]. A more viable excitation technique from the practical point of view is to use unbalanced forces, since these present naturally in rotary systems and are easy to control. However, in the majority of cases it has the disadvantage of only being applicable in balancing planes whose location is predetermined, and its magnitude varies with the square of the rotational velocity; consequently, the excitation of the rotor at low frequencies is weak. Even with these difficulties, the characterization of rotary systems confined to certain particular characteristics has been achieved, such as systems with light damping and isotropic systems [3]. For a more general case, characterization of rotary systems requires measuring the vibration from a point of the rotor caused by excitation forces applied to each DOF separately [4]. Currently, there are no works that report techniques or methodologies that use unbalanced forces of a rotor for modal characterization. In this work, a technique for modal characterization of a rotor using unbalance is presented, taking advantage of the use of finite element models for the numerical tests. From the numerical tests and the technique, extraction of the modal parameters is achieved, such as the eigenvalues and the right and left eigenvectors, in order to have a complete modal arrangement.

2. Models used for dynamic characterization

For dynamic characterization of structures, spatial models, modal models, or response models are used, depending on which parameters are more convenient to use in each type of engineering application, keeping in mind that there are relationships between the models which help to move from one model to another, according to the needs that may arise. The parameters in a spatial model are the inertial, dissipative, and elastic coefficients. These express the relationships between the accelerations, velocities, and displacements of different points of the system and the excitation forces that are applied to these points. These coefficients are commonly assembled in matrices known as mass, damping, and stiffness matrices, respectively [1]. A modal model is composed of eigenvalues (natural frequencies), right eigenvectors (modal forms), and left eigenvectors. There is a parameter of each type for each vibrational mode of the structure, and there are as many vibrational modes as there are DOFs in the structure. The last model is the response model, which is formed by frequency response functions (FRFs). These functions are normally assembled in a matrix commonly called an FRF matrix. The procedure for determining the modal parameters of a structure require measuring a column and a line of the FRF matrix. From any of these FRFs, the natural frequencies can be obtained, but a complete column is required in order to extract the right eigenvectors and a complete line in order to extract the left eigenvectors. This is equivalent to measuring a number, $N$ , of FRFs for a system of N DOFs. The main differences between the static structures and rotary structures that affect the characterization process are due to the following:

a) The rotary structures have properties that depend on velocity [5].

b) Response and excitation often operate on fixed or mobile reference frameworks. This can produce a complicated relationship between the excitation frequencies and those that operate on the response [6, 7].

c) The mathematical models of rotary structures generally involve asymmetrical matrices [2, 8].

2.1. Calculation of right eigenvectors

As noted above, a modal model is composed of eigenvalues and right and left eigenvectors. The extraction procedures and the significance of the first two are well established [1, 9, 10]. However, this is not the case for left eigenvectors. Therefore, in this section the basic equations for defining left and right eigenvectors developed for a vibratory structure in reference [11] are presented in order to show their significance, physical interpretation, and engineering applications. For this, a model of an undamped system is used, which due to its simplicity permits the main ideas to be expressed. This model obeys the following movement equation:

1

M \ddot{x} (t) + K x (t) = f (t), x (t), f (t) \in R .

For the case of an unforced system $(t) = 0$ , in which a harmonic response $x (t) = ϕ_{k} e^{i ω_{k} t}$ is considered, Eq. (1) can be expressed in the following manner, after premultiplying it by $M^{- 1}$ :

2

(M^{- 1} K) ϕ_{k} = ω_{k}^{2} ϕ_{k}, k = 1, \dots, n,

where $ϕ_{k}$ is the $k$ th right eigenvector and $ω_{k}^{2}$ the $k$ th natural frequency elevated to the square, or eigenvalue. The left eigenvalues appear in a similar construction, but unlike Eq. (2), they are pre-multiplied by the product $(M^{- 1} K)$ :

3

I_{k}^{T} (M^{- 1} K) = ω_{k}^{2} I_{k}^{T} .

The left and right eigenvectors are related in the following way:

4a

I_{k} = M ϕ_{k},

4b

L^{T} = ϕ^{- 1},

where $L = [I_{1} I_{2} \dots I_{n}]$ , $Φ = [ϕ_{1} ϕ_{2} \dots ϕ_{n}]$ .

The left and right eigenvectors are orthogonal to each other and these orthonormality relationships can be written as follows:

4c

I_{k}^{T} ϕ_{j} = δ_{k j} = \{\begin{matrix} 1, k = j, \\ 0, k \neq j . \end{matrix}

Substituting Eq. (4a) into Eq. (4c) the biorthogonality relationship between the eigenvectors is obtained:

4d

I_{k}^{T} M ϕ_{j} = δ_{k j} .

2.2. Physical interpretation of the eigenvectors

The $j$ th left eigenvector is proportional to the inertial force, $f_{j} (t)$ , which is related to the $j$ th vibrational mode:

5

f_{j} (t) = M \ddot{x} (t) = - ω_{j}^{2} M ϕ_{j} \sin ω_{j} t = = - ω_{j}^{2} I_{j} \sin ω_{j} t .

Multiplying Eq. (2) by $M,$ eigenvalues of the problem are obtained when resolving the following problem of characteristic values and vectors:

5a

K ϕ_{j} = ω_{j}^{2} M ϕ_{j} .

The above equation shows that the forces of inertia related to the $j$ th right eigenvectors are proportional to the elastic potential forces (modal forms). Substituting Eq. (5a) into Eq. (5), the following is obtained:

5b

f_{j} (t) = - K ϕ_{j} \sin ω_{j} t = - ω_{j}^{2} I_{j} \sin ω_{j} t .

The preceding equation shows that the left eigenvectors are proportional both to the inertial forces and the elastic potential forces for a particular natural frequency and therefore represent force relationships. The orthogonality relationships in Eqs. (4c)-(4d) can be described in terms of mechanical work. For example, the inertial forces and elastic potential forces related to the $k$ th mode do not carry out the mechanical work in other modes (example: in the $j$ th mode, where $k \neq j$ ). This point is of utmost importance in some areas, such as structural modification, modal analysis, and dynamic control of structures.

2.3. Engineering applications of left eigenvectors

Using the orthogonality relationships from Eq. (4c), the solution for Eq. (1) can be expressed using modal expansion:

6

x (t) = \sum_{k = 1}^{n} (ϕ_{k} ϕ_{k}^{T} \frac{1}{ω_{k}} \int_{0}^{t} f (t - τ) \sin ω_{k} τ d τ) .

The interpretation of the left eigenvectors as modal forces is used to show that each right eigenvector can be selectively controlled by means of its corresponding left eigenvector. In particular, a force vector parallel to the left eigenvectors can be selected in order to affect only a specific mode. For example:

7

f (t) = α (t) I_{j} .

According to Eq. (4c), only the response due to $ϕ_{j}$ is influenced by the force in Eq. (7). Substituting Eq. (7) into Eq. (6) the following is obtained:

8

x (t) = ϕ_{j} (\frac{1}{ω_{j}} \int_{0}^{t} α (t - τ) \sin ω_{k} τ d τ) .

The preceding equation can be used for the control of only a select set of modes in a desired frequency range. This is known as modal control. The foregoing can be interpreted as follows: the forces of inertia and potential are obliged to affect only specific modes, leaving the others unaffected. For this application, using left eigenvectors permits eliminating the influence of modal truncation and providing the desired control or exact modification of the dynamic systems [11]. Another application is in the field of modal analysis. Given the eigenvalues and eigenvectors, the modal decomposition of a system response can be formed. This permits the system to be transformed into a decoupled set of coordinates where left and right eigenvectors are being used. Thus, the FRF can be expressed as:

9

H_{p} = \sum_{r = 1}^{n} \frac{a_{r} ψ_{r} ϕ_{r}^{T}}{i ω - λ_{r}} + \frac{{\bar{a}}_{r} {\bar{ψ}}_{r} {\bar{ϕ}}_{r}^{T}}{i ω - {\bar{λ}}_{r}} .

The above equation relates the left and right eigenvectors $ψ_{r}$ and $ϕ_{r}$ . Obtaining the modal decomposition of a system has many benefits, such as modal parameter extraction or modal balancing [1].

3. Extraction of left and right eigenvectors using FRFs

The frequency response matrix of a vibratory system can be expanded into a series of eigenvectors [11]:

10

[H_{1} H_{2} \dots H_{n}] = \sum_{k = 1}^{n} \frac{1}{ω_{k}^{2} - ω_{}^{2}} ϕ_{k} ϕ_{k}^{T} .

An $H_{p}$ column of the matrix can be experimentally measured using a simple excitation (applied in the $p$ th point). This column can be expressed as:

11

H_{p} = \sum_{k = 1}^{n} \frac{ϕ_{k} [p]}{ω_{k}^{2} - ω_{}^{2}} ϕ_{k} = \sum_{k = 1}^{n} \frac{1}{ω_{k}^{2} - ω_{}^{2}} ψ_{k},

where the definition $ψ_{k} = ϕ_{k} [p]$ is used and $ϕ_{k} [p]$ is the $p$ th element of $ϕ_{k}$ .

In the Eq. (11), the $H_{p}$ vector is a linear combination of $ϕ_{k}$ modal vectors. The coefficients for this linear combination are $ϕ_{k} [p] / (ω_{k}^{2} - ω_{}^{2})$ , which are dependent on the frequency.

3.1. Extraction of right eigenvectors from measured FRFs

A column of the FRF matrix can be decomposed into:

12

H_{p} = [ψ_{1} ψ_{2} \dots] (\begin{matrix} \frac{1}{ω_{1}^{2} - ω_{}^{2}} \\ \frac{1}{ω_{2}^{2} - ω_{}^{2}} \end{matrix}) .

The natural frequencies $ω_{k}^{}$ can be identified with great accuracy using known methods [1]. The frequency response matrix is measured in a number of frequencies, $= Ω_{1}$ , $Ω_{2}$ , …. Assuming that all columns of the FRF (Eq. (12) transposed) were obtained:

13

[\begin{matrix} H_{1 p} (Ω_{1}) & H_{2 p} (Ω_{1}) & \dots \\ H_{1 p} (Ω_{2}) & H_{2 p} (Ω_{2}) & \dots \\ ⋮ & ⋮ \end{matrix}] = [\begin{matrix} \frac{1}{ω_{1}^{2} - Ω_{1}^{2}} & \frac{1}{ω_{2}^{2} - Ω_{2}^{2}} & \dots \\ \frac{1}{ω_{1}^{2} - Ω_{1}^{2}} & \frac{1}{ω_{2}^{2} - Ω_{2}^{2}} & \dots \\ ⋮ & ⋮ \end{matrix}] (\begin{matrix} ψ_{1} \\ ψ_{2} \\ ⋮ \end{matrix}) .

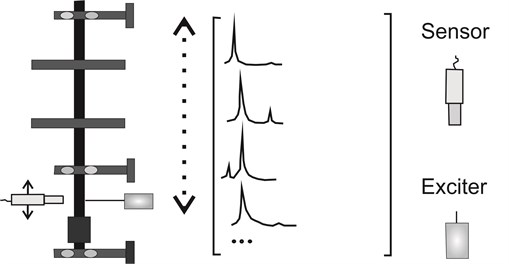
Whenever the FRF is measured with sufficient frequency resolution, the matrix coefficient (Eq. (13)) will have a range of $m$ , given that the matrix coefficients are composed of known natural frequencies and excitation frequencies. The Eq. (13) can be directly resolved for the m right eigenvectors in the measured range. This same equation is based on the supposition that all columns of the response matrix (FRF) were obtained. However, in order to obtain a column of this matrix, it is necessary to excite some system node and measure the remaining nodes, varying the measurement sensor. Fig. 1 shows the framework for obtaining a response matrix column from measurements carried out in a structure, in this case in a rotor.

Fig. 1Procedure for obtaining a column of the response matrix of a system

3.2. Extraction of left eigenvectors from measured FRFs

The extraction of left eigenvectors is more problematic due to the deficient range of the matrix coefficients. In physical terms, this deficiency in the range is due to the difficulty of obtaining the applied force given the measured response. The formulation tends toward a set of equations from which the left eigenvectors can be extracted.

Multiplying the $p$ th column of the FRF matrix by $I_{j}^{T}$ , the following equation can be written:

14

{I_{j}^{T} H}_{p} = \sum_{k = 1}^{n} \frac{ϕ_{k} [p]}{ω_{k}^{2} - ω_{}^{2}} {I_{j}^{T} ϕ}_{k} .

Substituting Eq. (4c) into Eq. (8), the following simplified equation is obtained:

15

{I_{j}^{T} H}_{p} = \sum_{k = 1}^{n} \frac{ϕ_{j} [p]}{ω_{j}^{2} - ω_{}^{2}} .

If some type of normalization is not considered for the left eigenvectors, the preceding equation is reduced to:

16

{I_{j}^{T} H}_{p} = \sum_{k = 1}^{n} \frac{1}{ω_{j}^{2} - ω_{}^{2}} .

The above equation can be evaluated for different frequencies $ω = Ω_{1}$ , $Ω_{2}$ ,… (e.g., selecting the appropriate inputs of the experimentally obtained FRF). Repeating Eq. (16) for $m$ left eigenvectors in the measured range, e.g., for $j =$ 1, 2,…, $m$ , the following is obtained:

17

[\begin{matrix} H_{1 p} (Ω_{1}) & H_{2 p} (Ω_{1}) & \dots \\ H_{1 p} (Ω_{2}) & H_{2 p} (Ω_{2}) & \dots \\ ⋮ & ⋮ \end{matrix}] [{\bar{I}}_{1} {\bar{I}}_{2} \dots] = [\begin{matrix} \frac{1}{ω_{1}^{2} - Ω_{1}^{2}} & \frac{1}{ω_{2}^{2} - Ω_{2}^{2}} & \dots \\ \frac{1}{ω_{1}^{2} - Ω_{1}^{2}} & \frac{1}{ω_{2}^{2} - Ω_{2}^{2}} & \dots \\ ⋮ & ⋮ \end{matrix}],

where ${\bar{I}}_{1}$ is the estimate of $I_{1}^{}$ .

The same equation can be written for each column of the FRF, e.g., $p =$ 1…, $n$ . When a test is carried out with multiple excitation forces, several FRF columns are measured and the additional information can be used to improve the accuracy of the estimations.

Writing Eq. (17) in matrix form for a single eigenvector, the following is obtained:

18

{A \bar{I}}_{k} = B_{k},

where $A$ is the matrix of coefficients and $B_{k}$ is the $k$ th column of the right side of the matrix in Eq. (17).

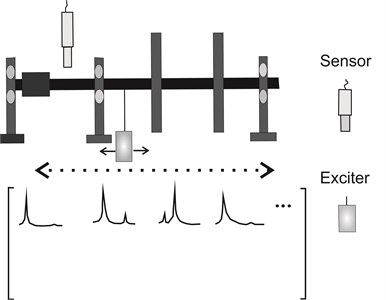
The extraction of the left eigenvectors of Eq. (13) consists of resolving an inverse problem, i.e., taking the measured response and deducing the forces (left eigenvectors) that cause it. Experimentally, the eigenvectors are extracted from a response matrix line. However, measuring an FRF matrix line poses serious practical difficulties. This is because it demands the application of excitation forces in each degree of freedom of the machine, as can be seen in Fig. 2.

4. Modal characterization of rotary machines

The need to determine the left eigenvectors for complete modal characterization of rotary structures has required that traditional modal analysis be modified in order to be applied to these systems.

Some current techniques for estimating modal parameters of rotary structures are limited to specific systems, such as the following:

• Undamped gyroscopic systems.

• Axisymmetric axle systems with isotropic supports.

• Axisymmetric axle systems mounted on a special type of anisotropic supports.

• Systems with small anisotropy or light damping.

For specific cases, it is possible to completely characterize the dynamic of a machine with few measured FRFs, but in a more general case, it is necessary to measure a complete line and column of the FRF matrix.

Fig. 2Procedure for obtaining a line from the response matrix of a system

4.1. Use of unbalanced forces for excitation

Taking advantage of the unbalanced forces permits a gyratory system to be excited without the need to connect it to excitation equipment, thus resolving the problem of difficult access. In general, this type of excitation is used for modal rotor balancing, which is a process based on the supposition that the rotors behave like structures and therefore that the effects of the gyroscopic effects are negligible. Although this supposition does not have significant effects on demarcated vibrational modes of gyroscopic forces, some modes can be strongly affected by said forces and it is these which cannot be adequately characterized following a structural approach. As noted above, modal characterization of systems affected by gyroscopic moments requires the application of unbalanced excitation forces in all DOFs. When unbalanced excitation forces are used, this is not generally possible, as the unbalanced masses can only be mounted on the balancing planes of the rotors; i.e., the rotors can only be excited from a limited number of DOFs. Therefore, it is impossible to measure the FRF matrix line required in order to characterize a gyroscopic system. In the majority of rotors, measuring an FRF matrix column is difficult due to the response only being measured at exposed points of the rotor. An extreme case is that of turbomachine rotors, in which the response can only be measured in the bearings due to the rotors being enclosed in a housing and/or at elevated temperatures.

4.2. Modal characterization of a rotor: numerical example

In order to present the process of modal characterization of a rotor via unbalance, the finite element method for modeling a semi-rigid rotor will be used. The Fig. 3 shows the rotor and its finite element model.

Table 1Properties of the supports

Right support	Left support
$k_{1} = [\begin{matrix} 1 & 0 \\ 0 & 1.2 \end{matrix}] \times 10^{3} N / m$ , $c_{1} = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] N.s / m$	$k_{2} = [\begin{matrix} 1 & - 0.7 \\ - 0.5 & 1.2 \end{matrix}] \times 10^{3} N / m$ , $c_{2} = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] N.s / m$

The rotor has a rigid axle with two rigid disks and is mounted on flexible damped supports. Its properties are shown in Table 1 [12].

The Fig. 4 shows the proposed framework in this work for characterizing the rotor using unbalanced excitation.

Fig. 3a) Dimensions of the rotor, b) finite element model [10]

a)

b)

Fig. 4Framework used for rotor characterization

For this numeric example, only 4 nodes of the finite node set of the rotor were taken as a reference in order to obtain a 4×4 response matrix with 16 internal elements. The procedure consists of utilizing the unbalanced force as a means of excitation. The unbalanced force is placed on a rotor node at the same time the measurements are taken in the remaining nodes. With this information, harmonic analyses are run in order to extract the responses from the model, and then structure the complete response matrix form the system study. Once the complete response matrix has been obtained, one matrix column is sufficient for extracting the frequencies and right eigenvectors. In order to extract the left eigenvectors, a line is taken from the response matrix. Fig. 5 shows the framework and the method of taking the measurements and assembling the response matrix.

The Fig. 6 shows the response diagram using unbalanced excitation, exciting response in node 40, and measured in 1, 13, 27, and 40.

For the motor shown, only the first 3 vibrational modes were considered. Tables 2, 3, and 4 show the results obtained for each vibrational mode of the rotor: eigenvalue and left and right eigenvectors.

Fig. 5Process for assembling a response matrix using unbalance

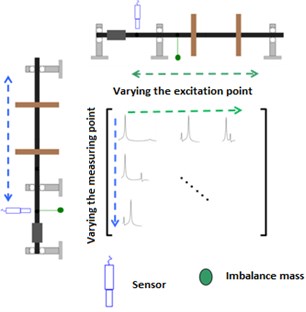
Fig. 6Responses obtained from the harmonic analysis: exciting in node 40 and measuring in nodes 1, 13, 27, 40

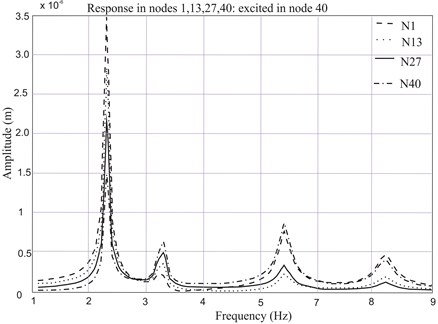
Table 2Eigenvalues and eigenvectors for mode 1

2.2932 Hz
Right eigenvector	0.0228 + 0.0038 $i$	0.0230 @ 9.4°	Left eigenvector	–0.025 – 0.043 $i$	0.05 @ 59.23°
	0.0153 + 0.0016 $i$	0.0153 @ 5.9°		–0.054 – 0.062 $i$	0.082 @ 49°
	0.0375 + 0.0080 $i$	0.0383 @ 12.04°		–0.082 – 0.081 $i$	0.1161 @ 44°
	0.0301 + 0.0059 $i$	0.0306 @ 11.09°		–0.110 – 0.10 $i$	0.1494 @ 42°

Table 3Eigenvalues and eigenvectors for mode 2

3.2546 Hz
Right eigenvector	0.0518 + 0.0004 $i$	0.051 @ 0.4°	Left eigenvector	–0.007 –0.109 $i$	0.109 @ 86°
	0.0667 + 0.0009 $i$	0.066 @ 0.8°		–0.002 – 0.094 $i$	0.094 @ 88°
	0.0215 + 0.0030 $i$	0.021 @ 8°		0.001 – 0.078 $i$	0.078 @ –89°
	0.0368+ 0.0017 $i$	0.036 @ 2.6°		0.028 + 0.039 $i$	0.048 @ 49°

Table 4Eigenvalues and eigenvectors for mode 3

5.0374 Hz
Right eigenvector	0.0669 + 0.0084 $i$	0.0674 @ 7.2°	Left eigenvector	–0.069 – 0.092 $i$	0.11 @ 53°
	0.1746 + 0.0053 $i$	0.1746 @ 1.7°		–0.031 – 0.036 $i$	0.04 @ 49°
	–0.1491 – 0.0354 $i$	0.1532 @ 13°		0.006 + 0.019 $i$	0.02 @ 72°
	–0.0411 – 0.0220 $i$	0.0466 @ 28°		0.044 + 0.075 $i$	0.08 @ 19°

5. Discussion

The modal parameters of a rotor or gyroscopic system are functions of the rotational velocity and existing works about modal characterization of rotors lead to a rotor model valid for a fixed rotational velocity. This can be useful when characterizing the rotor in stable conditions is desired, for example at its nominal operational velocity. Unlike previous works, the method presented here permits the modal parameters of each mode to be known separately while the rotor is passing the critical velocities associated with each. Although a complete model of the rotor at a specific velocity is not obtained through the proposed method, the parameters found are important because they permit to determine the parameters of a vibrational mode in the frequency intervals, in which the said modes predominate. There are engineering applications in which it is important to know the behavior of the rotor for an interval of velocities and not necessarily for a fixed velocity. In particular, for practical applications such as modal balancing of rotors, it is fundamental to know the right and left eigenvectors, mass, frequency, and modal damping of each of the vibrational modes of the motor when it passes through its critical velocities. The effectiveness of modal balancing will depend on the complete and correct characterization of each vibrational mode, which will lead to a better calculation of modal weight arrangement for balancing. Consequently, this lead to fewer test runs to balancing a rotor or even without test runs (saving money and time). The correct modal weight arrangement reduces the possibility of damaging the rotor structure in carrying out test runs in contrast to the influence coefficient method and the possibility of balancing a vibrational mode at a time without affecting the others modes.

Although a simplified rotor model was used here, this work opens the opportunity to develop patterns that helps fault detection of complex rotors by the eigenvector arrangement obtained. However, the proposed technique is applicable when there are sufficient balancing planes in order to extract the unbalance response.

6. Conclusions

With the solutions presented above, it follows that unbalanced force can be employed as a means of excitation for extracting the modal parameters of rotary structures or rotors using response models. From a numeric model, a response or FRF matrix could be constructed from the analyzed system to later extract the modal parameters and thus have a complete modal arrangement. The advantage of having a complete modal arrangement is that from relationships with spatial and response models the dynamic information from one model can be exported to another according to necessity, utility, or aims of the analyzed system. The results obtained with the characterization method presented here are especially relevant for cases in which correct identification of modal parameters at critical velocities is important, as is the case in modal rotor balancing.

References

Ewins D. J. Modal Testing: Theory, Practice and Application. Research Studies Press, Baldock, Hertfordshire, England. 2000.

Search CrossRef
Muszynska A. Modal testing of rotor/bearing systems. International Journal of Analytical and Experimental Modal Analysis, Vol. 1, Issue 3, 1986, p. 15-34.

Search CrossRef
Nordmann R. Identification of the modal parameters of an elastic rotor with oil film bearings. Transactions of the ASME Journal of Vibration, Acoustics and Reliability in Design, Vol. 106, Issue 1, 1984, p. 107-111.

Search CrossRef
Muszynska A. Aplication of sweep frequency rotating force perturbation methodology in rotating machinery for dynamic stiffeness identification. Translation of ASME, Vol. 115, 1993, p. 266-271.

Search CrossRef
Genta G. Whirling of unsymmetrical rotors: a finite element approach based on complex co-ordinates. Journal of Sound and Vibration Vol. 124, 1988, p. 27-53.

Search CrossRef
Lee C. W. A complex modal testing theory for rotating machinery. Mechanical Systems and Signal Processing, Vol. 5, 1991, p. 119-137.

Search CrossRef
Irretier H., Reuter F. Experimental Modal Analysis in Rotating Machinery. Final Report DFG, Universität/Gesamthochschule Kassel, 1994, (in German).

Search CrossRef
Han R. P., Zu J. Pseudo selfadjoint and non-selfadjoint systemas in structural dynamics. Journal of Sound and Vibration, Vol. 184, 1995, p. 725-742.

Search CrossRef
Figueroa R. A., Herrera M., Cruz P., Murillo I. Dynamic response in non-perpendicular stiff main directional rotors using coordinate transformation. Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 37, Issue 6, 2015, p. 1615-1622.

Search CrossRef
Figueroa R. A., Aguirre J. E., Cruz P., Murillo I., Herrera M. Application of coordinate transformation for detection of modes of vibration: a comparative study in 2 turbogenerators. Journal of Vibroengineering, Vol. 17, Issue 5, 2015, p. 2108-2120.

Search CrossRef
Bucher I., Braun S. G. Left eigenvectors: extraction from measurements and physical interpretation. ASME Journal of Applied Mechanics, Vol. 64, Issue 1, 1997, p. 97-105.

Search CrossRef
Gutiérrez E., Ewins D. J. Characterisation of rotating machinery structures within limited frequency intervals using modal analysis. Australian Journal of Mechanical Engineering, Vol. 2, Issue 1, 2005, p. 11-20.

Search CrossRef

About this article

Received

02 October 2015

Accepted

08 January 2016

Published

15 February 2016

SUBJECTS

Modal analysis

Keywords

modal characterization

response models

left-eigenvectors

unbalance response

Author Contributions

All authors have worked on this manuscript together and all authors have read and approved the manuscript. Pedro Cruz is the main researcher who initiated and organized the research reported in the paper. The preparation of manuscript was made under supervision and guidance of Profs. Enrique Gutiérrez and Dariusz Szwedowicz who supported on the sections mathematical and numerical. Rafael Figueroa designed the process of numerical simulation and results analyzed. Josefa Morales contributed to the sections mathematical and in the Final review. The reviewers’ comments were incorporated by all the authors.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.