Uncertainty analysis for cylindrical structure vibration according to generalized polynomial chaos method

Luyun, Chen; Yi, Hong

doi:10.21595/jve.2022.22254

Journal of Vibroengineering

Browse Journal

Submit article

Published: 23 June 2023

Check for updates

Uncertainty analysis for cylindrical structure vibration according to generalized polynomial chaos method

Chen Luyun¹

Hong Yi²

^{1, 2}State Key Laboratory of Ocean Engineering, MOE Key Lab Marine Intelligent Equipment and System, Shanghai Jiao Tong University, Shanghai, 200240, China

Corresponding Author:

Hong Yi

Cite the article Download PDF

Downloads 108

Abstract

Aiming to gain an accurate prediction model of the vibro-acoustic problem for the vibrating structure systems, the uncertainty vibration analysis for the cylindrical shell structure considering construction factors is investigated. The generalized polynomial chaos (GPC) method is used to gain the analytical solution of the free vibration for the cylindrical shell structure, in which the construction uncertainty factors, comprising the material uncertainty parameter and construction geometric uncertainty parameter, are considered. By combining the collocation method and generalized polynomial chaos method, the influence of the uncertainty construction factor on the free vibration properties for the cylindrical shell structure is verified by a numerical analysis. The results provide technical support for the design and construction of the vibrating structure for vibration and noise reducing.

Highlights

The uncertainty problem of vibro-acoustic characteristic considering of construction factors is investigated.
The collocation method and generalized polynomial chaos method be combined to deal with the uncertainty problem.
The effectiveness of the proposed method is compared by using Monte Carlo method.

1. Introduction

The noise and vibration level of the vibrating structure is an important index in evaluating the quality level in the structural design and construction. To predict the vibro-acoustic properties of the complex vibrating structure, establishing accurate analysis models is necessary, which include the theoretical analysis model and numerical analysis model. Despite the fact that the accuracy of the analysis models for the vibrating structure is constantly improving, some deviations between the numerical analysis results and measurement result for the practical engineering were still observed, the analysis results are only the approximate value of the practical engineering. The deviation caused by the uncertainty factors will lead to the analysis results exceeding the design permission value, the uncertainty problem cannot be avoided in practical engineering. In the process of structural construction, some inherent and random parameters exist. The uncertainty factors in the structural construction process include the material uncertainty parameter and construction geometric uncertainty parameter. These phenomena may lead to the fact that the vibro-acoustic parameters of the vibrating structure are essentially random variables with a certain probability density distribution. For example, the elastic modulus of structural material in the vibrating structure may be an uncertain value, while the uncertainty properties of the structural material would affect the vibro-acoustic properties. The uncertainty problem of construction factors shows that under a certain level of the construction technology, the influence of the uncertainty factors on the vibrating structure system cannot be eliminated, while improving the construction technology level can only narrow the uncertainty interval, and cannot eliminate it forever. Because some uncertainty factors exist in the course of structure construction, defining the vibro-acoustic property parameters as random variables with a certain probability density distribution is necessary [1-4]. If more than one uncertainty input parameters exist, the vibro-acoustic uncertainty problem may be more complex [5, 6].

The uncertainty quantification problem is a realistic and common way for representing uncertainty parameters, which cannot be assigned with deterministic values. The parameter value can be defined as a nominal deterministic value and the unknown part is represented as uncertainty. The requirement of the approach is such that the mathematical representation of the uncertain part can be developed by probability or possibility theories. To analyze the uncertainty problem of the vibro-acoustic properties, the commonly analysis method aims to evaluate the influence of uncertainty for each input parameter to the final result response, in which the probability statistical method be used to deal with those comprehensive effect degree analysis, respectively. Up to date uncertainty analysis techniques have been introduced to deal with the uncertainty problem of vibro-acoustic properties, which include the stochastic perturbation method [7, 8], Monte Carlo method, reliability analysis method [9-11], response surface method [12], and spectral stochastic method, and so on [13, 14]. The spectral decomposition method has been widely used because of its high computational efficiency in dealing with Gaussian or non-Gaussian distribution problems, such as the Fourier decomposition method, Karhunen-Loève method (KL), and so on [15-17]. Recently, the generalized polynomial chaos (GPC) has attracted more attention because of the advantages in solving non-Gaussian distribution problems and unknown covariance parameters problems[18-20]. In contrast to the sampling methods, e.g., Monte Carlo simulations, the polynomial chaos expansion is a non-sampling method that represents the uncertain quantities as an expansion, including the decomposition of deterministic coefficients and random orthogonal bases. In addition, the other advantage of the GPC method is that the deterministic coefficients of the truncated series need to be calculated only once in the solution process.

The uncertainty structural construction factors can be defined as nominal deterministic value, while the GPC method is applied to analyze the uncertainty vibro-acoustic problem for the cylindrical shell structure. The research scope is expanded from the random loading to the uncertainty of construction factors. The remainder of the present article is organized as follows: in Section 2, the basic principles of the GPC method are briefly described; in Section 3, the formulations of uncertainty of input parameter distribution is presented; in Section 4, the formulations of uncertainty conduction function is established by coupling the GPC method and collocation method; in Section 5, the cylindrical shell structure, for example, the feasibility and effectiveness of the proposed are illustrated; finally, some major conclusions are summarized in Section 6.

2. Generalized polynomial chaos (GPC) method

2.1. Concept of generalized polynomial chaos method

The GPC method is used to deal with the uncertainty vibro-acoustic problem. The core concept of generalized polynomial chaos (GPC) is to project the uncertainty parameters in the solving space into a random space, which comprised a set of complete orthogonal polynomials $Ψ_{i}$ , which contains the standard random variable $ξ$ . The standard random variable is a multidimensional standard random vector $ξ = \{ξ_{1}, ξ_{2}, \dots, ξ_{n}\}$ and each standard random variable corresponds to the random space $ξ_{i} \in Ω_{i}$ , $i = 1,2, \dots, n$ . According to the orthogonality properties of standard random variables and the complete orthogonal bases, the random parameters can be simplified and solved. The GPC method is used to determine the lower and upper bounds of the mean values and standard deviations of structural vibro-acoustic properties.

In the numerical analysis for the uncertainty vibro-acoustic problem for the complex vibrating structure, to define the corresponding polynomials, which can be matched for random distribution functions, is necessary. The calculation convergence and truncation number are dependent on the various polynomials chosen, while the appropriate matching polynomials can improve the calculation efficiency. The best matching combination of typical random distribution functions and their corresponding polynomials are shown in Table 1.

Table 1Uncertainty parameter types and the corresponding orthogonal polynomials

Random distribution of uncertainty parameters	Optimal polynomial type
Gaussian	Hermite
Gamma	Laguerre
Beta	Jacobi
Uniform	Legendre

2.2. Projection of generalized polynomial chaos method

Choosing a polynomial and the random space $(Ω, γ, P)$ is defined, where $Ω$ is the total sample space, $γ$ is the $σ$ domain of the sample space, and $P$ is the probability measure on $Ω$ . The uncertain parameter $χ : Ω \to R$ with finite variance, i.e., $χ \in L^{2} (Ω)$ , can be represented as:

1

χ = x_{0} Ψ_{0} + \sum_{i_{1} = 1}^{\infty} x_{i_{1}} Ψ_{1} (ξ_{i_{1}}) + \sum_{i_{1} = 1}^{\infty} \sum_{i_{2} = 1}^{i_{1}} x_{i_{1} i_{2}} Ψ_{2} (ξ_{i_{1}}, ξ_{i_{2}}) + \sum_{i_{1} = 1}^{\infty} \sum_{i_{2} = 1}^{i_{1}} \sum_{i_{3} = 1}^{i_{2}} x_{i_{1} i_{2} i_{3}} Ψ_{3} (ξ_{i_{1}}, ξ_{i_{2}}, ξ_{i_{3}}) + \dots,

where Eq. (1) can be written as short form $χ = \sum_{i = 0}^{\infty} x_{i} Ψ_{1} (ξ)$ . $Ψ_{i}$ is the random orthogonal basis and $x_{i}$ is the undetermined coefficient. The random orthogonal basis $Ψ_{i}$ is a set of polynomials that contain random vector $ξ$ , and it satisfies the orthogonality condition:

2

\{\begin{array}{l} E [Ψ_{i}, Ψ_{j}] = E [Ψ_{i}^{2}] δ_{i j} = h_{i}^{2} δ_{i j}, \\ E [Ψ_{i}, Ψ_{j}, Ψ_{k}] = h_{i j k}, \\ E [Ψ_{i}, Ψ_{j}, Ψ_{k}, Ψ_{l}] = h_{i j k l}, \end{array}

where $E [Ψ_{i}, Ψ_{j}] = \int_{Ω} Ψ_{i} (ζ) Ψ_{j} (ζ) ρ (ζ) d ζ$ . $E$ represents the expectation on the whole probability space, $δ_{i j}$ is the Kronecker delta, and $h_{i}$ is the norm of the probability density distribution function. $ρ (ζ)$ is the probability density distribution of the standard random variable $ζ$ , and it is often defined as standard normal distribution function, and it can be selected as a type of distribution function under special circumstances.

For the random parameter $χ$ , the probability density distribution is defined as $ρ (χ)$ , Eq. (1) can be written in shorthand:

3

χ = \sum_{i = 0}^{\infty} x_{i} Ψ_{i} (ξ) .

To solve the uncertainty problem, the convergence requirements is necessary, the number of items needs to be truncated for the random parameter, and the polynomial terms can be expressed as follows:

4

χ = \sum_{i = 0}^{N} x_{i} Ψ_{i} (ξ),

where $N = \frac{(n + p)!}{n! p!} - 1$ , $p$ is the highest order of the expansion, and $n$ is the dimension of the random vector.

In Eq. (1), the undetermined coefficient $x_{i}$ can be obtained by Galerkin projection on the orthogonal basis:

5

x_{k} = \frac{⟨χ (ζ), Ψ_{k} (ζ)⟩}{⟨Ψ_{k}^{2}⟩},

where, $⟨χ (ζ), Ψ_{k} (ζ)⟩ = E [χ (ζ), Ψ_{k} (ζ)] = \int_{Ω} χ (ζ) \cdot Ψ_{k} (ζ) \cdot ρ (ζ) d ζ$ , the first-order term in random orthogonal basis Ψ represents Gaussian distribution. Eq. (5) is the generalized polynomial chaos transformation function for the random parameter $χ$ , and the dimensional of random orthogonal basis directly reflects the complexity of random space, which is involved in the process of chaotic transformation. The Karhunen-Loève is a specific type of the GPC, the GPC expansion and Karhunen-Loève expansion can be converted to each other easily. The higher-order term in random orthogonal basis $Ψ$ represents non-Gaussian distribution. The total number of terms $N$ of the whole polynomial is determined by the dimensional of random orthogonal basis and the highest order $p$ of the expansion.

2.3. Solving the generalized polynomial chaos method

The GPC method can be used to solve the non-Gaussian random distribution problems. In the construction process of the vibrating structure, there are involve uncertainty parameters problem: geometric uncertainty, material uncertainty, initial condition uncertainty, boundary condition uncertainty, and so on. The application of the GPC method to solve the uncertainty problem of vibro-acoustic properties comprises three steps: first, the uncertainty parameters are expressed as a form of polynomial chaos expansion, while the coefficients of the expansion are obtained; second, the input parameters and the final response results are expressed as a form of polynomial chaos expansion; finally, the uncertainty properties of the input parameters is transformed by the structural governing equation, while the undetermined coefficient is gained. The solution process is shown in Fig. 1.

Fig. 1The GPC based solving flow chart

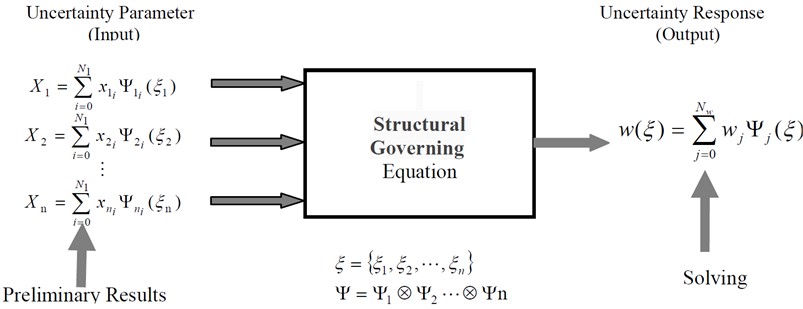
The probability density distribution of the input parameters (such as the density of structural materials, modulus of elasticity, Poisson’s ratio, thickness of plates and shells, type of ribs, and so on) in vibrating structures should be obtained in the procedure of the uncertainty analysis of the vibro-acoustic properties for the vibrating structures. According to the uncertain conduction function of the GPC method, the uncertainty properties of vibrating structures design parameters are transformed into the output parameters, while the probability density distribution of the vibro-acoustic properties of the vibrating structures are obtained. The whole calculation process is shown in Fig. 2.

3. Uncertainty input parameter processing

To solve the uncertainty problem of vibro-acoustic properties for the vibrating structure by using the GPC method, in which the undetermined coefficient $x_{i}$ in the GPC expression must be solved. If the random parameter $χ$ and $ξ$ are in the same random space, the two variables meet the same probability distribution, and the undetermined coefficient $x_{i}$ can be obtained by using the Galerkin projection method:

6

x_{i} = \frac{1}{⟨Ψ_{i}^{2} (ξ)⟩} \int_{a}^{b} χ (ζ) \cdot Ψ_{i} (ζ) \cdot ρ (ζ) d ζ,

where $a$ and $b$ are the upper and lower limits of standard random variables, $χ (ξ)$ is the probability density distribution function. If $χ (ξ)$ is an unknown function, the corresponding random space transformation must be conducted to obtain the expression $χ = F (ξ)$ , which relationship the random parameter $χ$ and standard random variables $ξ$ .

Defining the random parameter $χ$ in the random space $Ω_{1}$ , the probability distribution is $ρ_{1} (χ)$ , and the interval is $[c, d]$ ; similarly, defining the random parameter $ξ$ in the random space $Ω_{2}$ , the probability distribution is $ρ_{2} (ξ)$ , and the interval is $[a, b]$ . The transformation between uncertainty parameter and random variable are shown in Fig. 3.

Fig. 2The vibro-acoustic solution based on GPC

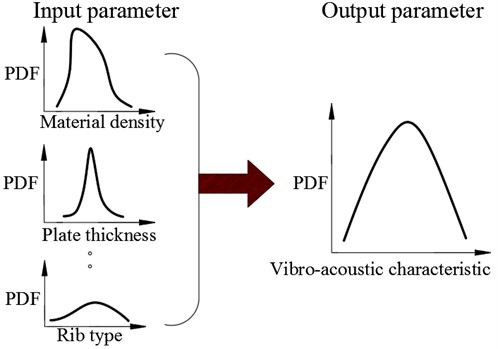
Fig. 3The transformation for uncertainty parameters and random variables

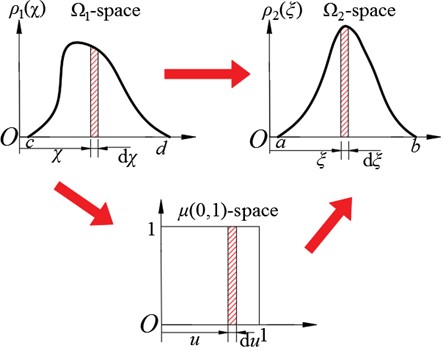
In Fig. 3, the transformation function between the random parameter $χ$ and standard random variables $ξ$ can be expressed as follows:

7

\int_{c}^{χ} ρ_{1} (τ) d τ = \int_{a}^{ξ} ρ_{2} (τ) d τ \Rightarrow χ = F (ξ) .

Substituting Eq. (7) into Eq. (6), then the undetermined coefficient $x_{i}$ can obtain as:

8

x_{i} = \frac{1}{⟨Ψ_{i}^{2}⟩} \int_{a}^{b} F (ξ) Ψ_{i} (ξ) ρ_{2} (ξ) d ξ .

However, in most cases, the random distribution function $F (ξ)$ may be an implicit expression. Therefore, the difficulty of solving the undetermined coefficient $x_{i}$ is increased, and it is necessary to introduce the standard average distribution as an intermediate variable to solve the problem. To implement the variable conversion, the transformation relationship between the random parameter $χ$ and standard random variables $ξ$ on the standard average distribution $μ (0,1)$ is established:

9

\{\begin{array}{l} \int_{0}^{1} 1 d μ = \int_{c}^{χ} ρ_{1} (τ) d τ \Rightarrow χ = F_{1} (u), \\ \int_{0}^{1} 1 d μ = \int_{a}^{ξ} ρ_{2} (τ) d τ \Rightarrow ξ = F_{2} (u) . \end{array}

Substituting Eq. (9) into Eq. (8), the undetermined coefficient $x_{i}$ can be obtained as:

10

x_{i} = \frac{1}{⟨Ψ_{i}^{2}⟩} \int_{0}^{1} F_{1} (u) Ψ_{i} (F_{2} (u) ξ) d u .

According to Eq. (11) and Eq. (5), the undetermined coefficient $x_{i}$ can be solved by projecting to the standard uniform distribution space.

4. The uncertainty conduction function

In this section, the influence of the uncertainty of the structural input parameters on the vibro-acoustic properties is investigated. The probability density distribution of the input parameters (structural materials, structural geometry, and so on) is effectively converted to the probability density distribution of the output parameters (dynamic response, acoustic radiation response, and so on) through the relevant mathematical model (dynamic control equation).

4.1. Collocation method

Despite the fact that the GPC method can be used to solve the uncertainty problems of the complex structure, in the application of the finite element model to analyze the vibro-acoustic properties problem of the complex structure, the deterministic stiffness matrix coefficient $k_{i}$ , the deterministic mass matrix coefficient $m_{i}$ , the deterministic mode vector coefficient $ϕ_{r i}$ and the deterministic natural frequency coefficient $λ_{r i}$ are involved. To obtain these coefficients, a large number of formula derivations and integral operations are required, and the calculation is time-consuming. Therefore, improving the conduction equation is necessary.

In addition, for most engineering structures, the probability density distribution $ρ_{1} (χ)$ of random parameter $χ$ may be unknown, it cannot be described by explicit function, and it can only be obtained through experiments. Therefore, obtaining the probability density distribution of the random parameter by using the collocation method and the experimental data is necessary.

The collocation method is a widely-used uncertainty calculation method in the engineering structure, which is based on the least square method. By minimizing the difference between the two prediction results and the related uncertainty parameters is gained. The collocation method and the GPC method can be combined to calculate the undetermined coefficient, while the calculation steps are as follows: first, selecting a set of standard random variables $\{ξ^{(1)}, ξ^{(2)}, \dots, ξ^{(n)}\};$ Second, according to Eq. (9), a set of uncertain parameters $\{χ^{(1)}, χ^{(2)}, \dots, χ^{(n)}\}$ can be obtained by the standard random variables. Based on the least square method, the difference between these uncertainty parameters and the parameters expressed by the GPC method can be expressed as:

11

Δ χ = {\sum_{i = 0}^{n} [χ^{(i)} - \sum_{j = 0}^{N} x_{j} Ψ_{j} (ξ^{(i)})]}^{2} .

To minimize the difference $Δ χ$ , the partial derivative for each coefficient is 0:

12

\frac{\partial (Δ χ)}{\partial x_{k}} = \sum_{i = 1}^{n} \{2 [χ^{(i)} - \sum_{j = 0}^{N} x_{j} Ψ_{j} (ξ^{(i)})] [- Ψ_{k} (ξ^{(i)})]\} = 0,

thus:

13

\sum_{i = 1}^{n} \sum_{j = 0}^{N} x_{j} Ψ_{j} (ξ^{(i)}) Ψ_{k} (ξ^{(i)}) = \sum_{i = 1}^{n} χ^{(i)} Ψ_{k} (ξ^{(i)}) .

The matrix form of the Eq. (7) can be written as follows:

14

[\begin{array}{l} \sum_{i = 1}^{n} Ψ_{0} (ξ^{(i)}) \cdot Ψ_{0} (ξ^{(i)}) & \sum_{i = 1}^{n} Ψ_{1} (ξ^{(i)}) \cdot Ψ_{0} (ξ^{(i)}) & \dots & \sum_{i = 1}^{n} Ψ_{N} (ξ^{(i)}) \cdot Ψ_{0} (ξ^{(i)}) \\ \sum_{i = 1}^{n} Ψ_{0} (ξ^{(i)}) \cdot Ψ_{1} (ξ^{(i)}) & \sum_{i = 1}^{n} Ψ_{1} (ξ^{(i)}) \cdot Ψ_{1} (ξ^{(i)}) & \dots & \sum_{i = 1}^{n} Ψ_{N} (ξ^{(i)}) \cdot Ψ_{1} (ξ^{(i)}) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ \sum_{i = 1}^{n} Ψ_{0} (ξ^{(i)}) \cdot Ψ_{N} (ξ^{(i)}) & \sum_{i = 1}^{n} Ψ_{1} (ξ^{(i)}) \cdot Ψ_{N} (ξ^{(i)}) & \dots & \sum_{i = 1}^{n} Ψ_{N} (ξ^{(i)}) \cdot Ψ_{N} (ξ^{(i)}) \end{array}] \{\begin{array}{l} x_{0} \\ x_{1} \\ ⋮ \\ x_{N} \end{array}\} = \{\begin{array}{l} \sum_{i = 1}^{n} (χ^{(i)} \cdot Ψ_{0} (ξ^{(i)})) \\ \sum_{i = 1}^{n} (χ^{(i)} \cdot Ψ_{1} (ξ^{(i)})) \\ ⋮ \\ \sum_{i = 1}^{n} (χ^{(i)} \cdot Ψ_{N} (ξ^{(i)})) \end{array}\} .

Therefore, the undetermined coefficient $x_{i}$ can be obtained by solving the matrix equation. The random parameter $χ$ can be obtained too. This method avoids the complex integral operation of Eq. (10) to solve the coefficient directly, which greatly reduces the calculation complexity and calculation time.

4.2. Solving the collocation method

To improve the efficiency of the uncertainty analysis of vibro-acoustic properties problem, the collocation method and GPC method are used to solve the uncertainty problem of the input parameters and structural output response parameters, the probability density distribution of structural response is obtained. The solution process is shown in Fig. 4.

Fig. 4The solution process based on collocation method

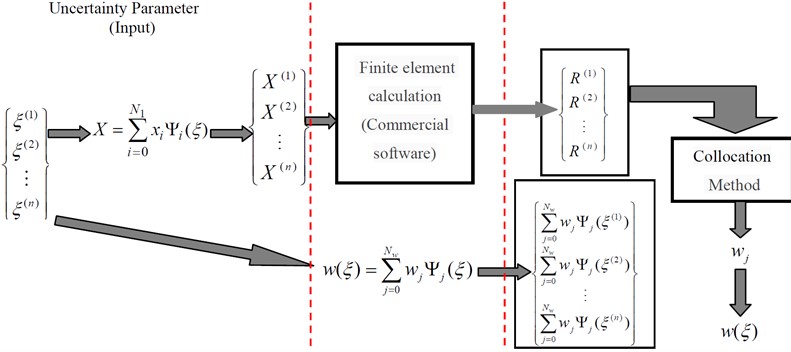
As shown in Fig. 4, by combining the collocation method and GPC method, the mature finite element commercial software can be directly used to solve the uncertainty problem, which can simplify the calculation process and improve the calculation efficiency. The Galerkin projection method is used to determine the uncertainty parameters, while the collocation method is used to calculate the vibro-acoustic properties.

5. Numerical analysis and discussion

5.1. Model description

The cylindrical shell structure (the GPC and Monte Carlo methods) is used to calculate its natural frequency to verify the correctness of the propose method.

An infinite thin-walled cylindrical shell for example, the cylindrical coordinate system ( $x$ , $θ$ , $r$ ) is established to define the position of the cylindrical shell, and the boundary conditions are simply supported at both ends, as shown in Fig. 5.

The design parameters of cylindrical shell structure are as follows: mean radius $R =$ 3.25 m, length $L =$ 40.0 m, shell thickness $h =$ 0.04 m. The cylindrical shell structure is made of structural steel with the following mechanical performance parameters: density, $ρ =$ 7860 kg/m³; modulus of elasticity, $E =$ 210 GPa; Poisson ratio, $μ =$ 0.3.

5.2. Numerical analysis

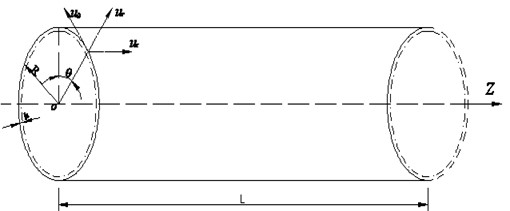
The elastic modulus of the shell structure is selected as a random variable, while its distribution satisfied the lognormal normal distribution $L N (μ, σ)$ , expectation $E =$ 2.1×10¹¹ Pa, variance $V a r = 0.03 E$ . According to the lognormal normal distribution, there is $μ = l o g (\frac{E^{2}}{\sqrt{V a r + E^{2}}})$ , $σ = \sqrt{l o g (\frac{V a r}{E^{2}} + 1)}$ , the probability density function (PDF) is shown in Fig. 6.

Fig. 5Coordinate system of cylindrical shells

The probability density distribution of the first four natural frequencies of the structure is calculated by the GPC and Monte Carlo methods. In the GPC method, the Hermite polynomials are used to fit the uncertain elastic modulus with the highest order of 3.

Fig. 7 has shown the comparison diagram of the calculation results of the first-order natural frequency by the GPC and Monte Carlo methods with various simulation times.

Fig. 6The Elastic Modulus PDF

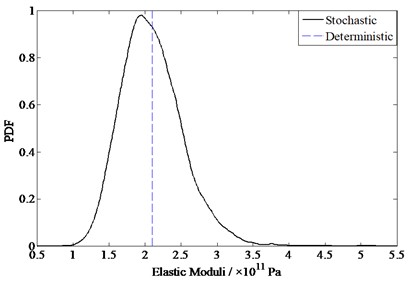
Fig. 7The 1st order natural frequency comparison between GPC and different order MC

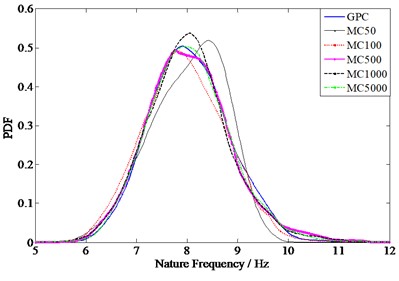
Fig. 8 shows the comparison diagram of the calculation results of each order natural frequency by the GPC method and the 5000 simulation Monte Carlo method.

As shown in Figs. 5 to 8, the calculation results of the GPC method are consistent with those of the Monte Carlo method, the correctness of the coupling GPC method and collocation method in solving vibro-acoustic properties problems are verified.

5.3. Calculation efficiency

To verify the effectiveness of the proposed method, the calculation simulation times of the GPC method and Monte Carlo method is compared, as shown in Table 2.

Table 3 shows that in the case of a similar result accuracy, 5000 times of simulation Monte Carlo method needs 134518.3 seconds, while the GPC method only needs 184.2 seconds, and the calculation time is far less than that of the Monte Carlo method. Because of unaffordable computational times, the Monte-Carlo method is unsuitable for practical engineering problems and is usually used as a reference method to verify the accuracy of other methods. The advantage and potential of the GPC method in solving the uncertain vibration problems of large-scale structures are fully demonstrated. It shows the advantages and potential of GPC method in solving the uncertainty problems of the vibro-acoustic properties for large-scale structure engineering.

Fig. 8The natural frequency comparison between GPC method and 5000 MC

a) The 1st order natural frequency

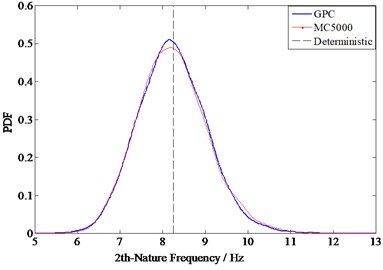
b) The 2nd order natural frequency

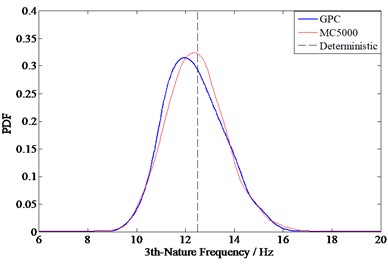
c) The 3st order natural frequency

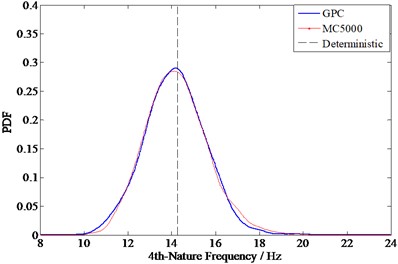
d) The 4nd order natural frequency

Table 2Consuming times between GPC and Monte Carlo

Calculation method	Simulation times	Calculation time (s)	Note
Monte Carlo	50	1445.0
	100	2884.3
	500	14542.8
	1000	29144.6
	5000	134518.3
Generalized polynomial chaos	( $n =$ 3, $p =$ 6)	184.2	$n$ is the highest order of polynomial, $p$ is the number of collocation points be selected

6. Conclusions

The cylindrical shell structure (the GPC and collocation methods) is combined to conduct the vibro-acoustic properties uncertainty analysis, in which the uncertainty of structural construction factors is transmitted and reflected in the probability density distribution. The feasibility and effectiveness of the proposed method are verified by numerical calculation, wherein the results show that the proposed method has a good robustness with respect to uncertainty. Results can be applied to the accurate prediction of the vibro-acoustic properties of vibrating structures and provide strategies for the acoustic quality control of the vibrating structure considering of construction factors.

References

F. Wu et al., “Interval and subinterval perturbation finite element-boundary element method for low-frequency uncertain analysis of structural-acoustic systems,” Journal of Sound and Vibration, Vol. 462, cNo. 9, p. 114939, Dec. 2019, https://doi.org/10.1016/j.jsv.2019.114939

Publisher
W. Gao, D. Wu, C. Song, F. Tin-Loi, and X. Li, “Hybrid probabilistic interval analysis of bar structures with uncertainty using a mixed perturbation Monte-Carlo method,” Finite Elements in Analysis and Design, Vol. 47, No. 7, pp. 643–652, Jul. 2011, https://doi.org/10.1016/j.finel.2011.01.007

Publisher
Z. Qiu and X. Wang, “Parameter perturbation method for dynamic responses of structures with uncertain-but-bounded parameters based on interval analysis,” International Journal of Solids and Structures, Vol. 42, No. 18-19, pp. 4958–4970, Sep. 2005, https://doi.org/10.1016/j.ijsolstr.2005.02.023

Publisher
Q. Chen, Q. Fei, S. Wu, and Y. Li, “Uncertainty propagation of the energy flow in vibro-acoustic system with fuzzy parameters,” Aerospace Science and Technology, Vol. 94, No. 9, p. 105367, Nov. 2019, https://doi.org/10.1016/j.ast.2019.105367

Publisher
J. Lin, W. Zhang, and J. Li, “Structural responses to arbitrarily coherent stationary random excitations,” Computers and Structures, Vol. 50, No. 5, pp. 629–633, Mar. 1994, https://doi.org/10.1016/0045-7949(94)90422-7

Publisher
G. Chen, G. Zhao, and B. Chen, “Sensitivity analysis of coupled structural-acoustic systems subjected to stochastic excitation,” Structural and Multidisciplinary Optimization, Vol. 39, No. 1, pp. 105–113, Jul. 2009, https://doi.org/10.1007/s00158-008-0320-x

Publisher
X. Guo, W. Bai, and W. Zhang, “Extreme structural response analysis of truss structures under material uncertainty via linear mixed 0-1 programming,” International Journal for Numerical Methods in Engineering, Vol. 76, No. 3, pp. 253–277, Oct. 2008, https://doi.org/10.1002/nme.2298

Publisher
Z. Xia and J. Tang, “Characterization of dynamic response of structures with uncertainty by using Gaussian processes,” Journal of Vibration and Acoustics, Vol. 135, No. 5, pp. 1006–1013, Oct. 2013, https://doi.org/10.1115/1.4023998

Publisher
C. Soize, “A comprehensive overview of a non-parametric probabilistic approach of model uncertainties for predictive models in structural dynamics,” Journal of Sound and Vibration, Vol. 288, No. 3, pp. 623–652, Dec. 2005, https://doi.org/10.1016/j.jsv.2005.07.009

Publisher
J.-F. Durand, C. Soize, and L. Gagliardini, “Structural-acoustic modeling of automotive vehicles in presence of uncertainties and experimental identification and validation,” The Journal of the Acoustical Society of America, Vol. 124, No. 3, pp. 1513–1525, Sep. 2008, https://doi.org/10.1121/1.2953316

Publisher
H.-R. Bae, R. V. Grandhi, and R. A. Canfield, “An approximation approach for uncertainty quantification using evidence theory,” Reliability Engineering and System Safety, Vol. 86, No. 3, pp. 215–225, Dec. 2004, https://doi.org/10.1016/j.ress.2004.01.011

Publisher
R. D.’Amico, A. Pratellesi, N. Baldanzini, and M. Pierini, “Reformulation of the Stochastic BEM to improve the computational efficiency in the prediction of the vibro-acoustic behaviour of structures with uncertainties,” Journal of Sound and Vibration, Vol. 332, No. 9, pp. 2132–2148, Apr. 2013, https://doi.org/10.1016/j.jsv.2012.09.012

Publisher
C. P. Rupert and C. T. Miller, “An analysis of polynomial chaos approximations for modeling single-fluid-phase flow in porous medium systems,” Journal of Computational Physics, Vol. 226, No. 2, pp. 2175–2205, Oct. 2007, https://doi.org/10.1016/j.jcp.2007.07.001

Publisher
K. Sepahvand, S. Marburg, and H.-J. Hardtke, “Numerical solution of one-dimensional wave equation with stochastic parameters using generalized polynomial chaos expansion,” Journal of Computational Acoustics, Vol. 15, No. 4, pp. 579–593, Dec. 2007, https://doi.org/10.1142/s0218396x07003524

Publisher
J. Hu, S. Chen, A. Behrangi, and H. Yuan, “Parametric uncertainty assessment in hydrological modeling using the generalized polynomial chaos expansion,” Journal of Hydrology, Vol. 579, No. 12, p. 124158, Dec. 2019, https://doi.org/10.1016/j.jhydrol.2019.124158

Publisher
K. Sepahvand, S. Marburg, and H.-J. Hardtke, “Uncertainty quantification in stochastic systems using polynomial chaos expansion,” International Journal of Applied Mechanics, Vol. 2, No. 2, pp. 305–353, Jun. 2010, https://doi.org/10.1142/s1758825110000524

Publisher
K. Yeo, Y. Hwang, X. Liu, and J. Kalagnanam, “Development of hp-inverse model by using generalized polynomial chaos,” Computer Methods in Applied Mechanics and Engineering, Vol. 347, No. 4, pp. 1–20, Apr. 2019, https://doi.org/10.1016/j.cma.2018.12.022

Publisher
H.-P. Wan, W.-X. Ren, and M. D. Todd, “Arbitrary polynomial chaos expansion method for uncertainty quantification and global sensitivity analysis in structural dynamics,” Mechanical Systems and Signal Processing, Vol. 142, No. 1, p. 106732, Aug. 2020, https://doi.org/10.1016/j.ymssp.2020.106732

Publisher
H. Tang, X. Guo, L. Xie, and S. Xue, “Experimental validation of optimal parameter and uncertainty estimation for structural systems using a shuffled complex evolution metropolis algorithm,” Applied Sciences, Vol. 9, No. 22, p. 4959, Nov. 2019, https://doi.org/10.3390/app9224959

Publisher
C. V. Verhoosel, M. A. Gutiérrez, and S. J. Hulshoff, “Iterative solution of the random eigenvalue problem with application to spectral stochastic finite element systems,” International Journal for Numerical Methods in Engineering, Vol. 68, No. 4, pp. 401–424, Oct. 2006, https://doi.org/10.1002/nme.1712

Publisher

About this article

Received

14 October 2021

Accepted

25 April 2022

Published

23 June 2023

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2022.22254

Keywords

cylindrical shell structure

uncertainty analysis

free vibration

generalized polynomial chaos (GPC)

collocation method

Acknowledgements

This work was partially supported by the Fund of High-tech Ship Research Projects by MIIT and State Key Laboratory of Ocean Engineering. This support is gratefully acknowledged by the authors.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 06 07

Vibration of circumferentially stepped-thickness piezoelectric cylindrical shells

Ata Meshkinzar, Ahmed M Al-Jumaily

Research article

2019 03 31

Analysis on circumferential natural frequencies of stator in permanent magnet synchronous motor

Shuangshuang Zhong, Shenbo Yu

Research article

2018 10 19

The optimization analysis on the vibration control of cylindrical shell with dynamic vibration absorber attached

Junjie Zhang

Research article

2017 08 15

Free vibration analysis of moderately thick isotropic homogeneous open cylindrical shells using improved Fourier series method

Fazl e Ahad, Dongyan Shi, Zarnab Hina, Rehman Anees Ur

C. Luyun and H. Yi, “Uncertainty analysis for cylindrical structure vibration according to generalized polynomial chaos method,” Journal of Vibroengineering, Vol. 25, No. 4, pp. 655–666, Jun. 2023, https://doi.org/10.21595/jve.2022.22254

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2022.22254
UR  - https://doi.org/10.21595/jve.2022.22254
TI  - Uncertainty analysis for cylindrical structure vibration according to generalized polynomial chaos method
T2  - Journal of Vibroengineering
AU  - Luyun, Chen
AU  - Yi, Hong
PY  - 2023
DA  - 2023/06/23
PB  - JVE International Ltd.
SP  - 655-666
VL  - 25
IS  - 4
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Luyun_2023,
	doi = {10.21595/jve.2022.22254},
	url = {https://doi.org/10.21595/jve.2022.22254},
	year = 2023,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {25},
	number = {4},
	pages = {655--666},
	author = {Chen Luyun and Hong Yi},
	title = {Uncertainty analysis for cylindrical structure vibration according to generalized polynomial chaos method},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]C. Luyun and H. Yi, “Uncertainty analysis for cylindrical structure vibration according to generalized polynomial chaos method,” Journal of Vibroengineering, vol. 25, no. 4, pp. 655–666, Jun. 2023, doi: 10.21595/jve.2022.22254.

Copy IEEE

Copied to clipboard!

Luyun, Chen, and Hong Yi. “Uncertainty Analysis for Cylindrical Structure Vibration According to Generalized Polynomial Chaos Method.” Journal of Vibroengineering 25, no. 4 (June 23, 2023): 655–66. https://doi.org/10.21595/jve.2022.22254.

Copy Chicago

Copied to clipboard!

Uncertainty analysis for cylindrical structure vibration according to generalized polynomial chaos method

Abstract

Highlights

1. Introduction

2. Generalized polynomial chaos (GPC) method

2.1. Concept of generalized polynomial chaos method

2.2. Projection of generalized polynomial chaos method

2.3. Solving the generalized polynomial chaos method

3. Uncertainty input parameter processing

4. The uncertainty conduction function

4.1. Collocation method

4.2. Solving the collocation method

5. Numerical analysis and discussion

5.1. Model description

5.2. Numerical analysis

5.3. Calculation efficiency

6. Conclusions

References

About this article

Related Articles