Dynamic response of a space flexible arm with a moving mass

1. Introduction

The vibration of structures under moving mass or moving load is an important engineering problem, such as a bridge with travelling vehicles and a robotic arm carrying a moving end effecter. Because of the importance of such problems in engineering, it has attracted the attention of many researchers in the last few decades. There are a lot of works can be found in the published literature.

In most studies, the structures are considered to be no rotating. Wu [1] investigated the dynamic response of an inclined beam excited by moving mass and the moving mass element is used in his analysis. Yang et al. [2] presented an analytical study on the free and forced vibration of inhomogeneous Euler–Bernoulli beams containing open edge cracks, and the beam is subjected to an axial compressive force and a concentrated transverse load moving along the longitudinal direction. Under different boundary conditions, Kiani et al. [3] gave a comprehensive assessment of design parameters for various beam theories subjected to a moving mass. A non-linear viscoelastic foundation supported finite Euler-Bernoulli beam with moving mass is studied by Ansari et al. [4], and the Galerkin method is used to discretize the non-linear partial differential equation of motion. Esen [5] investigated the dynamic behavior of a beam carrying accelerating mass. Then He [6] presented a modified finite element method that can be used to analyze the transverse vibrations of a Timoshenko beam subjected to a variable-velocity moving mass. Nikkhoo et al. [7] proposed a new orthogonal basis for the spatial discretization tracking the dynamic response of shear deformable beams with moving mass. Uzzal et al. [8] presented the dynamic response of an Euler-Bernoulli beam supported on two-parameter Pasternak foundation subjected to moving load as well as moving mass. Wang et al. [9] developed a high-order shear deformable beam model and investigated the transient response of a sandwich porous beam when acted upon by a non-uniformly distributed moving mass. Jena, Parhi and other authors [10-15] studied cracked structures subjected to moving mass problems. Besides, Parida, Jena and others [16-21] investigated the dynamic and static problems of composite structures.

The problem becomes more difficult if the structures rotate about an axis. For a rotating structure with moving mass, the interaction between rigid and flexible body motions is highly demanded. Some of the researchers studied the dynamic response of rotating shaft subject to moving mass or moving load. Different beam theories are employed to model the rotating shaft with a moving load by Katz et al. [22]. Lee [23] analyzed dynamic response of a rotating shaft subject to axial force and moving loads by using Timoshenko beam theory and the assumed mode method. Shiau [24] investigated the dynamic response of a rotating multi-span shaft with general boundary conditions subjected to an axially moving load. Other researchers studied the dynamic responses of structures rotating in a plane and exited by moving mass or moving load. Choura [25] investigated the reduction of residual vibrations for the position control of a flexible rotating beam carrying a payload mass. Fung and Yau [26] studied the vibration frequencies of a clamped-free flexible beam rotating in a horizontal plane and carrying a moving mass. And they [27] derived the equation of motion of the system which took into account the effect of centrifugal stiffening due to the rotation of the beam. Ouyang and Wang [28] presented a dynamic model for the vibration of a rotating Timoshenko beam subjected to a three-directional load moving in the axial direction. Lv et al. [29] developed a Fourier Spectral method (FSM) for the vibration analysis of a rotating Rayleigh beam exited by moving force.

To the author's knowledge, arm with a moving mass that rotates in both horizontal and vertical planes has not been reported. In this problem, the rotation motion of the arm in one plane will affect the deflection in the other. In order to find out the influence of the rotating motion of the beam in two planes on the deflections, this study is done. The dynamic equation of the structure is a system of binary second-order linear differential equations. Based on the central difference method, an algorithm is designed to solve the coupled equations. The influences of the rotation motion of the arm in two planes and the influences of the angle between the arm and the horizontal plane on the deflection in two planes were studied. In addition, the influences of moving mass and moving load on the deflection of the arm were compared.

2. Formulation of the equations of motion

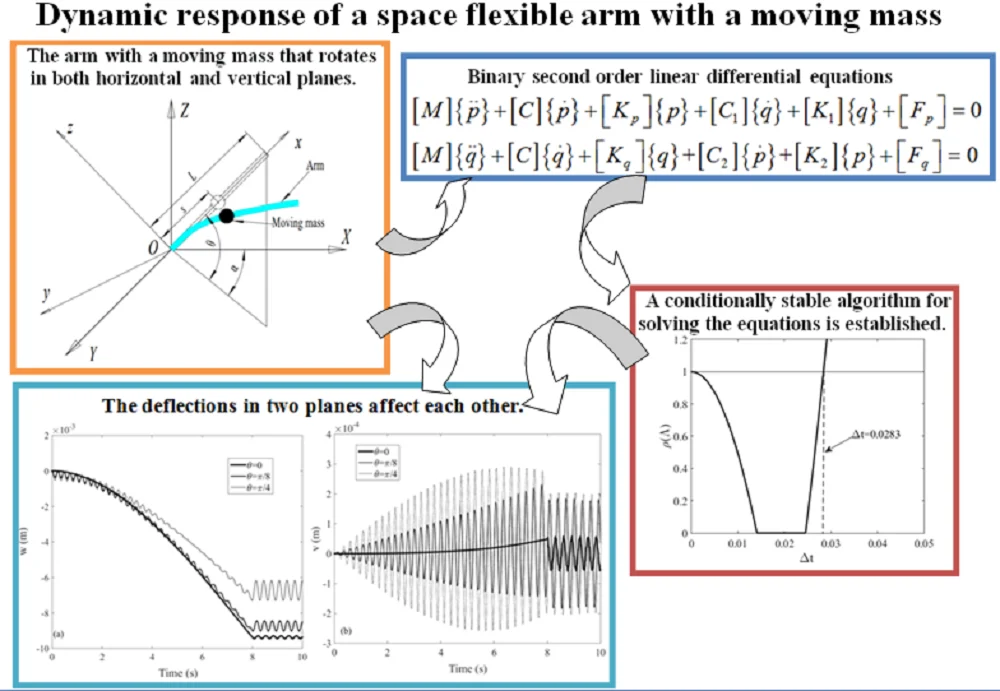
A uniform space rotating flexible arm with a moving mass is displayed in Fig. 1. $XYZ$ is the global reference frame, while $xyz$ is the rotating reference frame. The fixed end of the arm is located at point $O$ and the $x$ axis is directed along the undeformed configuration of the arm. The Angle between the $x$-axis and the $XOY$ plane is denoted as $\theta$. In this studying, 0 $<\theta <\pi$/2 is considered. The angular displacement of the arm rotates about $Z$ axis is denoted as $\alpha$. The moving mass $m$ moves along the arm. The length of the arm is $L$, $s\left(t\right)$ is the displacement of the moving mass in the $x$ direction while $\dot{s}\left(t\right)$ and $\ddot{s}\left(t\right)$ are the velocity and acceleration of the moving mass relative to the arm respectively.

The global position of an arbitrary material point $p$ on the arm can be expressed as:

where $A$ is the rotational transformation matrix from the rotating coordinate system $xyz$ to the fixed reference frame $XYZ$. It can be expressed as:

where:

are the rotational transformation matrices of the coordinate system $xyz$ rotating about the $Z$ axis and the $Y$ axis respectively. $r_p$ is the location of the point $p$ in the rotating coordinate system $xyz$ and can be written as:

where $v$ and $w$ are the lateral displacements along $y$ and $z$ axis respectively. The velocity of the point $p$ is:

Fig. 1A space rotating flexible arm with moving mass

The kinetic energy of the arm can be written as:

where ${\rho }_b$, $A_b$ and $J_b$ are the mass density, cross sectional area and the rotational inertia of the arm respectively. Based on Euler-Bernoulli beam theory [30], the elastic potential energy $U_s$ of the arm are given by:

where $E$ is the modulus of elasticity, $I_z$ and $I_y$ are the moment of inertia of arm section to z axis and $y$ axis respectively. And the gravitational potential energy $U_{gb}$ is:

The axial inertial force $F_x$ consists of centrifugal force [27] and gravity can be written as:

Thus, potential energy generated by $F_x$ can be written as:

Now, let us consider the kinetic energy and potential energy of the moving mass. The location of the moving mass in the rotating coordinate system $xyz$ can be written as:

and the velocity is:

Thus, the velocity of the moving mass in the fixed reference frame $XYZ$ is expressed as:

For a concentrated moving mass, the kinetic energy is:

The gravitational potential energy can be written as:

The total kinetic energy $T$ and potential energy $U$ of the system can be expressed as:

Lagrange’s equation with the assumed mode method is used to determine the equation of motion of the structural system. To use the assumed mode method, the flexible displacements of the arm can be expressed in terms of the generalized coordinates and displacement shape functions:

where $\left[\varphi \right]=\left[{\varphi }_1,\cdots ,{\varphi }_n\right]$, $\left\{p\right\}=\left\{p_1,\cdots ,p_n\right\}$ and $\left\{q\right\}=\left\{q_1,\cdots ,q_n\right\}$. For cantilevered beam, the shape functions are:

where ${\lambda }_i$ is obtained from the following characteristic equation:

Lagrange’s equation is written as:

Substituting the energy expressions into Eq. (22), the equations of motion of the whole structural system are gotten:

where:

3. Solution of the equations

3.2. Stability

To analyze the stability of the method we consider a single-degree-of-freedom (SDOF) system [32]:

41

$m\cdot \ddot{p}\left(t\right)+c\cdot \dot{p}\left(t\right)+k_p\cdot p\left(t\right)+c_1\cdot \dot{q}\left(t\right)+k_1\cdot q\left(t\right)+f_p=0,$

42

$m\cdot \ddot{q}\left(t\right)+c\cdot \dot{q}\left(t\right)+k_q\cdot q\left(t\right)-c_1\cdot \dot{p}\left(t\right)+k_{2}p\left(t\right)+f_q=0.$

The stability can be evaluated with the solution succinctly written in the recursive form [31, 32]:

43

$\left[\begin{array}{c}{p}_{i+1}\\ p_i\\ q_{i+1}\\ q_i\end{array}\right]=\mathrm{\Lambda }\left[\begin{array}{c}{p}_i\\ p_{i-1}\\ q_i\\ q_{i-1}\end{array}\right]+Z,$

and the amplification matrix $\mathrm{\Lambda }$ is expressed as:

44

$\mathrm{\Lambda }=\frac{1}{4+4\xi \mathrm{\Delta }t+\mathrm{\Delta }{t}^2\left({\xi }^2+{\xi }_1^2\right)}$
$\times \left[\begin{array}{cccc}8+4\mathrm{\Delta }t\xi -4\mathrm{\Delta }{t}^2{{\omega }_p}^2+2\mathrm{\Delta }{t}^3\left({\xi }_1{{\omega }_2}^2-\xi {{\omega }_p}^2\right)& -4+\mathrm{\Delta }{t}^2\left({\xi }^2+{\xi }_1^2\right)& -4\mathrm{\Delta }t{\xi }_1-4\mathrm{\Delta }{t}^2{{\omega }_1}^2+2\mathrm{\Delta }{t}^3\left({\xi }_1{{\omega }_q}^2-\xi {{\omega }_1}^2\right)& 4\mathrm{\Delta }t{\xi }_1\\ 4+4\xi \mathrm{\Delta }t+\mathrm{\Delta }{t}^2\left({\xi }^2+{\xi }_1^2\right)& 0& 0& 0\\ 4\mathrm{\Delta }t{\xi }_1-4\mathrm{\Delta }{t}^2{{\omega }_2}^2-2\mathrm{\Delta }{t}^3\left(\xi {{\omega }_2}^2+{\xi }_1{{\omega }_p}^2\right)& -4\mathrm{\Delta }t{\xi }_1& 8+4\mathrm{\Delta }t\xi -4\mathrm{\Delta }{t}^2{{\omega }_q}^2-2\mathrm{\Delta }{t}^3\left({\xi }_1{{\omega }_1}^2+\xi {{\omega }_q}^2\right)& -4+\mathrm{\Delta }{t}^2\left({\xi }^2+{\xi }_1^2\right)\\ 0& 0& 0& 4+4\mathrm{\Delta }t\xi +\mathrm{\Delta }{t}^2\left({\xi }^2+{\xi }_1^2\right)\end{array}\right],$

where $\xi =c/m$, ${\xi }_1=c_1/m$, ${{\omega }_p}^2=k_p/m$, ${{\omega }_q}^2=k_q/m$, ${{\omega }_1}^2=k_1/m$, ${{\omega }_2}^2=k_2/m$, The stability of an algorithm depend upon the eigenvalues of the amplification matrix. The stability condition is [31, 32]:

45

$\rho \left(\mathrm{\Lambda }\right)\le 1,$

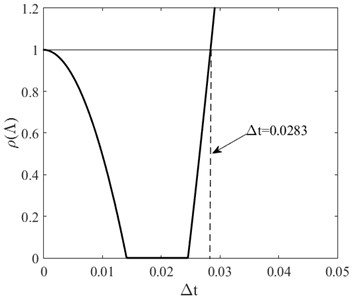
where $\rho \left(\mathrm{\Lambda }\right)$ is the spectral radius of $\mathrm{\Lambda }$ which is defined as $\rho \left(\mathrm{\Lambda }\right)=\mathrm{m}\mathrm{a}\mathrm{x}\left|{\lambda }_i\right|$, and ${\lambda }_i$ are the eigenvalues of $\mathrm{\Lambda }$. In this analysis, $m=$1, $c=$1, $c_1=$1, $k_p=$5000, $k_q=$5000, $k_1=$1, $k_2=$1. The value of $\rho \left(\mathrm{\Lambda }\right)$ is plotted against $\mathrm{\Delta }t$ in Fig. 2. It can be seen that when $\mathrm{\Delta }t\le 0.0283$, the algorithm is stable. Thereby, it is a conditionally stable algorithm.

Fig. 2Spectral radius of the amplification matrix.

4. Numerical simulation

4.1. Validation

In order to validate the equations of motion and computer program in this paper, comparisons with the results available in the open literature are made. A flexible arm with moving mass rotates in a horizontal plane about $Z$ axis is considered in [27]. Therefore $\theta$, $\dot{\theta }$ and $\ddot{\theta }$ in the program are all zero. To be consistent with [27], the non-dimensional parameters are defined as follows:

46

$\xi =\frac{x}{L},s_0=\frac{s}{L},N=\frac{m}{\rho AL},u=\frac{\nu }{L},T=\frac{t}{L^2}\sqrt{\frac{E{I}_z}{{\rho }_b{A}_b}},\eta =\dot{\alpha }{L}^2\sqrt{\frac{{\rho }_b{A}_b}{E{I}_z}},$

$\eta$ and $s_0$ are given by:

$\eta =\frac{f\left(T\right)\dot{g}\left(T\right)-\dot{f}\left(T\right)g\left(T\right)}{f^2\left(T\right)+g^2\left(T\right)},s_0=\frac{f\left(T\right)\dot{f}\left(T\right)+g\left(T\right)\dot{g}\left(T\right)}{\sqrt{f^2\left(T\right)+g^2\left(T\right)}},$

where:

47

$f\left(T\right)=\left\{\begin{array}{l}{x}_1+\frac{x_2-x_1}{T_t}\left[T-\frac{T_t}{2\pi }\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{2\pi T}{T_t}\right)\right],\begin{array}{ll}& 0\le T<T_t\end{array},\\ x_2,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}T\ge T_t,\end{array}\right.$

48

$g\left(T\right)=\left\{\begin{array}{l}{y}_1+\frac{y_2-y_1}{T_t}\left[T-\frac{T_t}{2\pi }\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{2\pi T}{T_t}\right)\right],\begin{array}{ll}& 0\le T<T_t\end{array},\\ y_2,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}T\ge T_t,\end{array}\right.$

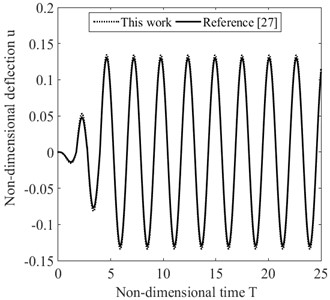
and $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$ are the initial and final position of the moving mass with reference to the axes $Oxy$ respectively, and $T_t$ is the traveling time of the mass. In this simulation, the mass moves towards the free end from (0.025, 0.2) to (0.8, 0.1), and other parameters are $N=$0.5, $T=$ 25, and $T_t=$5. Non-dimensional deflections of arm under the moving mass are shown in Fig. 3. It is observed that the deflection obtained by the present work is in good agreement with that of Ref. [27].

Fig. 3Non-dimensional deflection of arm under the moving mass

4.2. Simulation examples

A uniform space rotating flexible arm with a moving mass as Fig. 1 is considered. The material of the arm is steel, which $E=$209 GPa, ${\rho }_b=$ 7800 kg/m³. The dimensions of the system are $L=$2 m, $I_y=I_z=$1.33×10^-8 m⁴, $A_b=$ 4×10^-4 m², and the moving mass $m=$1 kg. In the following analysis, we take $\mathrm{\Delta }t$= 0.001.

First, three cases are used to study the influence of the rotating motion in horizontal and vertical planes on the lateral displacements. The mass moves towards the free end from the fixed end, and the initial conditions are: $s=$0, $\theta$ = 0, $\nu$ = 0, $w=$0, $\dot{\nu }$ = 0, $\dot{w}$ = 0. The movement rules of the system are given as follows:

49

$\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{}1:\left\{\begin{array}{l}\dot{s}=0.25\mathrm{}\mathrm{m}/\mathrm{s},\mathrm{}\mathrm{}\mathrm{}\dot{\alpha }=0.4\pi \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s},\mathrm{}\mathrm{}\mathrm{}\dot{\theta }=0,\mathrm{}\mathrm{}\mathrm{}0<t\le 5,\\ \dot{s}=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\alpha }=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\theta }=0,\mathrm{}5<t,\end{array}\right.$

50

$\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{}2:\left\{\begin{array}{l}\dot{s}=0.25\mathrm{}\mathrm{m}/\mathrm{s},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\alpha }=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\theta }=0.04\pi \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s},\mathrm{}\mathrm{}\mathrm{}\mathrm{}0<t\le 5,\\ \dot{s}=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\alpha }=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\theta }=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}5<t,\end{array}\right.$

51

$\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{}3:\left\{\begin{array}{l}\dot{s}=0.25\mathrm{}\mathrm{m}/\mathrm{s},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\alpha }=0.4\pi \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\theta }=0.04\pi \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s},\mathrm{}\mathrm{}\mathrm{}0<t\le 5,\\ \dot{s}=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\alpha }=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\theta }=0,\mathrm{}\mathrm{}\mathrm{}5<t.\end{array}\right.$

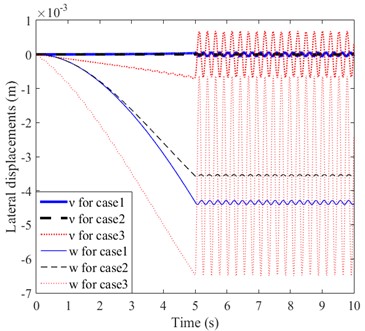
The arm rotates in the horizontal plane in case1 while it rotates in the vertical plane in case 2, and it rotates both in horizontal and vertical planes in case 3. After the travelling time passed (5$<t$), there is no mass and arm motion in the three cases. Fig. 4 shows the lateral displacements ($\nu$ and $w$) of free end of the arm in horizontal and vertical plane. It can be observed from Fig. 4 that the lateral displacements of case3 are larger than that of case1 and case 2. That is to say, under the same conditions, compared with rotating motion of the arm only in one plane (horizontal or vertical plane), rotating motion of the arm in the other plane at the same time will increase the lateral displacements in both planes. This is due to the coupling of lateral displacements in the two planes.

Fig. 4Lateral displacements of arm under the moving mass in case 1, 2 and 3

Next, the influence of the angle between the arm and the horizontal plane and the rotation acceleration of the arm on the lateral displacement is investigated. In case 4, the mass still moves from the fixed end to the free end, and the movement rules of the system are given as follows:

52

$\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{}4:\left\{\begin{array}{l}\dot{s}=0.25\mathrm{}\mathrm{m}/\mathrm{s},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\alpha }=\frac{\pi }{8}\mathrm{}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\theta }=0,\mathrm{}\mathrm{}\mathrm{}0<t\le 8,\\ \dot{s}=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\alpha }=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\theta }=0,\mathrm{}\mathrm{}\mathrm{}8<t.\end{array}\right.$

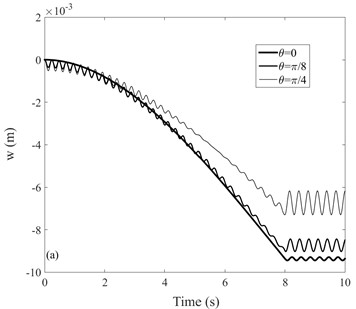
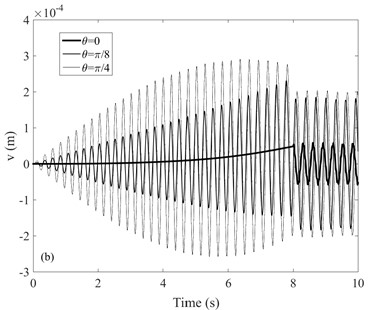
The arm rotates around the $Z$ axis with a constant angular velocity, and let $\theta$ be 0, $\pi /8$ and $\pi /4$ respectively. The initial conditions are: $s=$0, $\nu$= 0, $w=$0, $\dot{\nu }$ = 0, $\dot{w}$ = 0. The lateral displacements of free end of the arm are shown in Fig. 5. The transverse component of gravity of the moving mass decreases with the increase of $\theta$. Thereby, it can be seen clearly from Fig. 5(a) that in the steady state vibration phase ($t>$8 s) the tip lateral displacements $w$ decrease with the increase of $\theta$. This is caused by the decrease of the component force of gravity along the normal direction of the arm. However, the tip lateral displacements $\nu$increase with the increase of $\theta$. According to Eq. (24), the increase of $\theta$ will cause the decrease of stiffness matrix [$K_q$]. Therefore, the lateral displacements $\nu$ increases accordingly.

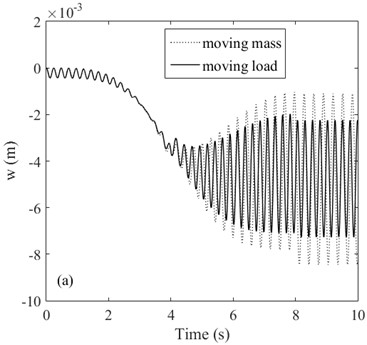
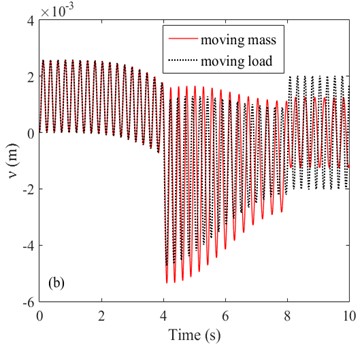
Finally, comparison between moving load and moving mass responses is carried out. In case 8 the mass moves from the fixed end to the free end, first with constant acceleration and then with constant deceleration. The initial and final velocities of the mass are both 0. The angular velocities of the arm in both horizontal and vertical plane also experienced a process of uniform increase at first and then uniform decrease, and their initial and final values are also 0. The dynamic responses of the arm under both moving load and moving mass conditions are considered. It can be observed from Fig. 6 that in the steady state vibration phase ($t>$8 s), the lateral displacement $w$ of moving mass is larger than that of moving load while the lateral displacement $\nu$ of moving load is larger than that of moving mass:

53

$\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{}5:\left\{\begin{array}{l}\ddot{s}=\frac{1}{8}\mathrm{}\mathrm{m}/{\mathrm{s}}^2,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\ddot{\alpha }=\frac{\pi }{16}\mathrm{}\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\ddot{\theta }=\frac{\pi }{48}\mathrm{}\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2,\mathrm{}\mathrm{}0<t\le 4,\\ \ddot{s}=-\frac{1}{8}\mathrm{}\mathrm{m}/{\mathrm{s}}^2,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\ddot{\alpha }=-\frac{\pi }{16}\mathrm{}\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\ddot{\theta }=-\frac{\pi }{48}\mathrm{}\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2,\mathrm{}\mathrm{}\mathrm{}4<t\le 8,\\ \dot{s}=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\alpha }=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\dot{\theta }=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}8<t.\end{array}\right.$

Fig. 5Lateral displacements of arm under the moving mass in case 4

a)$w$

b)$v$

Fig. 6Lateral displacements of arm under the moving mass in case 5

a)$w$

b)$v$

5. Conclusions

The problem of a space rotating flexible arm with a moving mass is investigated in this study. One end of the arm is fixed at the coordinate origin. The arm can rotate in both horizontal and vertical planes, and the lateral displacement in both planes is considered. The assumed mode method conjunction with Lagrange’s equation is used to derive the equations of the system. Then a set of coupled equations about the lateral displacements in the horizontal and vertical planes is obtained. Based on the central difference method, an algorithm is designed to solve the coupled equations. By numerical analysis, the following conclusions can be drawn:

1) The algorithm designed in this paper for solving binary second-order linear differential equations is a conditionally stable algorithm.

2) Due to the coupling of lateral displacements of the arm in horizontal and vertical planes, the increase of the angular velocity in one plane will increase the lateral displacements in the other plane.

3) When the angle between the arm and the horizontal plane $\theta$ increases, the component of gravity along the normal direction of the beam will decrease, resulting in a decrease in lateral displacements $w$, however, it will lead to a decrease in stiffness in horizontal plane and thus an increase in lateral displacements $\nu$.

4) Compared with moving mass, moving load ignores the influence of inertial force, so the calculation results of moving mass and moving load are different. In the steady state vibration phase, the lateral displacement w of moving mass is larger than that of moving load while the lateral displacement$\nu$ of moving load is larger than that of moving mass.