Active vibration control of rotating beam with moving mass using piezoelectric actuator

The robotic arm carrying a moving end effector can be modeled as a rotating beam with moving mass. Active vibration control of rotating beam with moving mass using piezoelectric actuator is presented. Simply supported beam and cantilevered beam are considered in this studying. The equations of the system are derived by Lagrange’s equation with the assumed mode method. The linear classical optimal control algorithm with displacement-velocity feedback is used to determine the control voltage. The numerical simulations reveal that the transverse displacements of the beam can be effectively reduced by the actuators. The effect of rotational speed and acceleration to the dynamic responses of the beam are also investigated.

Active vibration control of rotating beam with moving mass using piezoelectric actuator

Highlights

The vibration control of rotating beam with moving mass is studied.
Using piezoelectric materials as the actuator.
The equations of the system are derived by Lagrange’s equation.
The displacement-velocity feedback is used to determine the control voltage.
The simulation results show that the vibration of the structure is effectively suppressed.

1. Introduction

Piezoelectric materials have been more and more often applied to improve structural behavior. Such materials can actuate forces by electrical excitation, making them suitable as actuators for vibration control. Besides, they can sense deformation and generate a real-time voltage signal. Therefore, they can be used as sensor as well. Many researchers applied the piezoelectric actuator/sensor pairs to control the vibration of structures [1-6]. While other researchers used the piezoelectric actuators only to suppress the dynamic vibration of structures [7-12]. And some control algorithm is used to determine the control voltage.

The problem of the structures under the influence of moving loads or moving mass are of technological importance and has attracted the attention of many researchers in the last few decades. There are a lot of works can be found in the published literature [9-19]. And we can find some studies in the literature about active vibration control of dynamic response of such structures using piezoelectric actuator. Sung [9] and Nikkhoo et al. [10] studied the active control of a simply supported Euler-Bernoulli beam under a moving mass using piezoelectric actuator, respectively. And latter, Nikkhoo et al. [11] investigated the vibration control of a single span Euler-Bernoulli beam with geometrically nonlinear behavior under an arbitrary dynamic loading. Rofooei and Nikkhoo [12] investigated a thin rectangular plate with a number of piezoelectric patches bonded on its surface under the excitation of a moving mass. The moving mass is assumed to travel along linear and orbiting path over the plate respectively. In these studies, a linear classical optimal control algorithm with displacement-velocity feedback is used to determine the control voltage.

The problem becomes more difficult if the beam rotates around one end of it. For example, the robotic arm carrying a moving end effector rotates in the vertical plane. For a rotating beam with moving mass, the interaction between rigid and flexible body motions is highly demanded. To the author’s knowledge, active vibration control of beam with a moving mass that rotates in the vertical plane using piezoelectric actuator has not been reported. The author of this paper has studied this problem. Simply supported beam as well as cantilevered beam are considered. Lagrange’s equation with the assumed mode method is employed to derive the equations of motion. The linear classical optimal control algorithm with displacement-velocity feedback is used to determine the control voltage. Finally, a number of examples are presented to evaluate the control effect.

2. Formulation of the equations of motion

A uniform simply supported beam with moving mass is displayed in Fig. 1. One support base of the beam is fixed, and the other one can rotates around the fixed one. $X Y Z$ is the global reference frame, while $x y z$ is the rotating reference frame. Angle between the rotating reference frame $x y z$ and the global reference frame $X Y Z$ is denoted as $θ$ . In this studying, 0 ≤ $θ$ < $π$ /2 is considered.

Fig. 1A rotating simply supported beam with moving mass

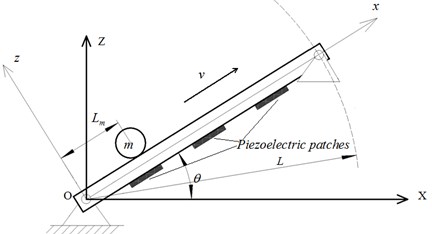
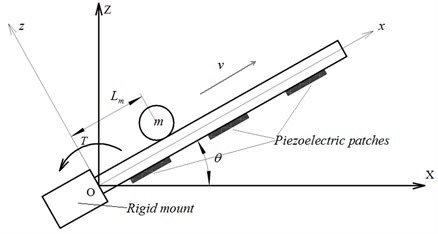
The moving mass moves along the beam. $m$ and $v$ are the mass and traveling speed of the moving mass respectively. $L_{m} = v t + 0.5 \dot{v} t^{2}$ is the displacement of the moving mass in the $x$ direction. The moving mass experiences a combination of rotational and linear motion. The transverse and axial vibration deformation of the beam in the reference frame $x y z$ is denoted as $w$ and $u$ respectively. There are $N_{p}$ piezoelectric patches as the actuators are bonded on the bottom surface of the beam and positioned by the coordinates $x_{i}$ and $x_{i}$ + $L_{p}$ $(i =$ 1, 2, …, $N_{p})$ in the reference frame $x y z$ . $L_{p}$ is the length of the piezoelectric patches. $h$ and $h_{p}$ are the thicknesses of the beam and piezoelectric patches, respectively. The width of the beam and the piezoelectric patches are both $b$ . Fig. 2 shows a cantilevered beam with moving mass. One end of the beam is fixed to a rigid mount and the other end is free. Torque $T$ rotates the rigid mount about $Y$ axis.

Fig. 2A rotating cantilever beam with moving mass

Euler-Bernoulli beam theory is employed to analyze the beam. The normal stress and strain of the beam in the axial direction are expressed as:

1a

σ_{x} = E ε_{x},

1b

ε_{x} = \frac{\partial u}{\partial x} - z \frac{\partial^{2} w}{\partial x^{2}},

where $E$ is the elastic modulus, $u$ and $w$ are the axial and vertical displacements, respectively. Let the piezoelectric patches be polarized along the $z$ direction. The axial stress, strain and the electrical displacement of the piezoelectric patches can be expressed as:

2a

σ_{x}^{p} = c_{11} ε_{x}^{p} - e_{31} E_{z},

2b

ε_{x}^{p} = \frac{\partial u}{\partial x} - z \frac{\partial^{2} w}{\partial x^{2}},

2c

D_{z} = e_{31} ε_{x}^{p} + \in_{33} E_{z},

where $c_{11}$ is the elastic stiffness, $D_{z}$ is the electrical displacement, $E_{z} = V (t) / h_{p}$ is the electrical field in the $z$ direction [6] and $V (t)$ is the external applied voltage. $\in_{33}$ is the dielectric constant, and $e_{31}$ is the piezoelectric constant.

The global position of an arbitrary material point p on the beam can be expressed as:

3

R_{p} = A \cdot r_{p},

where $A$ is the rotational transformation matrix from the moving coordinate system $x z$ to the fixed reference frame $X Z$ and $r_{p}$ is the location of the point $p$ in the rotating coordinate system $x z$ , they can be written as:

4a

A = [\begin{matrix} c o s θ & - s i n θ \\ s i n θ & c o s θ \end{matrix}],

4b

r_{p} = {[\begin{array}{l} x + u & w \end{array}]}^{T} .

The velocity of an arbitrary material point $p$ is:

5

{\dot{R}}_{p} = A \cdot {\dot{r}}_{p} + \dot{θ} \frac{d A}{d θ} r_{p},

where $\dot{θ}$ is the angular velocity of the beam, and:

6

{\dot{r}}_{p} = {[\begin{array}{l} \dot{u} & \dot{w} \end{array}]}^{T} .

Substituting Eq. (4) and Eq. (6) into Eq. (5), we will arrive at:

7

{\dot{R}}_{p} = \{\begin{array}{l} (\dot{u} - w \dot{θ}) c o s θ - [(x + u) \dot{θ} + \dot{w}] s i n θ \\ (\dot{u} - w \dot{θ}) s i n θ + [(x + u) \dot{θ} + \dot{w}] c o s θ \end{array}\} .

The kinetic energy of the beam can be written as:

8

K_{b} = \frac{1}{2} \int_{0}^{L} ρ_{b} A_{b} {\dot{R}}_{p}^{T} {\dot{R}}_{p} d x + \frac{1}{2} J_{b} {\dot{θ}}^{2} + \frac{1}{2} \sum_{i = 1}^{N_{p}} (\int_{x_{i}}^{x_{i} + L_{p}} ρ_{p} A_{p} {\dot{R}}_{p}^{T} {\dot{R}}_{p} d x + J_{p i} {\dot{θ}}^{2}),

where $ρ_{b}$ and $ρ_{p}$ are the mass density, and $A_{b} = b h$ and $A_{p} = b h_{p}$ are the cross-sectional area of the beam and the piezoelectric patches respectively. $J_{b}$ and $J_{p i}$ are the rotational inertia of the beam and the piezoelectric patches respectively. By substituting for the value of ${\dot{R}}_{p}$ from Eq. (7) and making use of some trigonometric properties, the kinetic energy of the beam can be expressed as:

9

K_{b} = \frac{1}{2} \int_{0}^{L} ρ_{b} A_{b} {\bar{V}}_{b}^{2} d x + \frac{1}{2} J_{b} {\dot{θ}}^{2} + \frac{1}{2} \sum_{i = 1}^{N_{p}} (\int_{x_{1}}^{x_{1} + L_{p}} ρ_{p} A_{p} {\bar{V}}_{b}^{2} d x + J_{p i} {\dot{θ}}^{2}),

where:

10

{\bar{V}}_{b}^{2} = (\dot{u} - w \dot{θ})^{2} + {[(x + u) \dot{θ} + \dot{w}]}^{2} .

The strain energy of the beam, and the strain energy and electric potential energy of the piezoelectric patches can be written as:

11

U_{s} = \frac{1}{2} \int_{0}^{L} \int_{- h / 2}^{h / 2} b σ_{x} ε_{x} d z d x + \frac{1}{2} \sum_{i = 1}^{N_{p}} \int_{x_{i}}^{x_{i} + L_{p}} \int_{- h / 2 - h_{p}}^{- h / 2} b (σ_{x}^{p} ε_{x}^{p} - D_{z} E_{z}) d z d x .

Substituting Eq. (1) and Eq. (2) into Eq. (11), we can obtain:

12

U_{s} = \frac{1}{2} \int_{0}^{L} (E A_{b} {u^{'}}^{2} + E I_{b} {w^{''}}^{2}) d x + \frac{1}{2} \sum_{i = 1}^{N_{p}} \int_{x_{i}}^{x_{i} + L_{p}} [c_{11} A_{p} {u^{'}}^{2} + c_{11} I_{p} {w^{''}}^{2} + 2 α u^{'} w^{''}

- 2 (β_{1} u' + β_{2} w'') V_{i} (t) - β_{3} V_{i}^{2} (t)] d x,

where:

I_{b} = \frac{b h^{3}}{12}, I_{p} = \frac{1}{3} b [{(\frac{h}{2} + h_{p})}^{3} - {(\frac{h}{2})}^{3}], α = \frac{b h_{p} (h + h_{p})}{2},

β_{1} = e_{31} b, β_{2} = \frac{e_{31} b (h + h_{p})}{2}, β_{3} = \frac{b \in_{33}}{h_{p}},

and $V_{i} (t)$ is the control voltage of the $i$ th piezoelectric patch. The gravitational potential energy of the beam can be written as:

13

U_{g b} = \frac{1}{2} ρ_{b} A_{b} g L^{2} s i n θ + \sum_{i = 1}^{N_{p}} ρ_{p} A_{p} g L_{p} (x_{i} + \frac{L_{p}}{2}) s i n θ .

Now, let us consider the kinetic energy and potential energy of the moving mass. For a concentrated moving mass, the kinetic energy is:

14

K_{m} = \frac{1}{2} \int_{0}^{L} [δ (x - L_{m}) m \cdot \frac{D R_{p}^{T}}{D t} \frac{D R_{p}}{D t}] d x,

where:

15

\frac{D R_{p}}{D t} = \{\begin{array}{l} (\dot{u} - w \dot{θ}) c o s θ - [(x + u) \dot{θ} + \frac{d w}{d t}] s i n θ \\ (\dot{u} - w \dot{θ}) s i n θ + [(x + u) \dot{θ} + \frac{d w}{d t}] c o s θ \end{array}\},

and:

16

\frac{d w}{d t} = \dot{w} + v w^{'} .

Substituting Eq. (15) into Eq. (14), we will get:

17

K_{m} = \frac{1}{2} \int_{0}^{L} \{δ (x - L_{m}) m \cdot [(\dot{u} - w \dot{θ})^{2} + {((x + u) \dot{θ} + \dot{w} + v w')}^{2}]\} d x .

The gravitational potential energy of the concentrated moving mass can be written as:

18

U_{g m} = \int_{0}^{L} δ (x - L_{m}) m g [(u + x) s i n θ + w c o s θ] d x .

The total kinetic energy and potential energy of the system can be expressed as:

19

K = K_{b} + K_{m},

20

U = U_{s} + U_{g b} + U_{g m} .

Lagrange’s equation with the assumed mode method is used to determine the equation of motion of the structural system. To use the assumed mode method, the flexible displacements of the beam can be expressed in terms of the generalized coordinates and displacement shape functions:

21a

u (x, t) = \sum_{i = 1}^{n} ψ_{i} (x) \cdot χ_{i} (t) = [ψ] \cdot {\{χ\}}^{T},

21b

w (x, t) = \sum_{i = 1}^{n} ϕ_{i} (x) \cdot q_{i} (t) = [ϕ] \cdot {\{q\}}^{T},

where $[ψ] = [ψ_{1}, \dots, ψ_{n}]$ , $\{χ\} = \{χ_{1}, \dots, χ_{n}\}$ , $[ϕ] = [ϕ_{1}, \dots, ϕ_{n}]$ and $\{q\} = \{q_{1}, \dots, q_{n}\}$ . For simply supported beam, the shape functions can be written as:

22a

ψ_{i} (x) = c o s \frac{i π}{L} x,

22b

ϕ_{i} (x) = s i n \frac{i π}{L} x, i = 1,2, \dots, n,

while for cantilevered beam, the shape functions are:

23a

ψ_{i} (x) = s i n \frac{(2 i - 1) π}{2 L} x

23b

ϕ_{i} = [c o s h (λ_{i} \frac{x}{L}) - c o s (λ_{i} \frac{x}{L})] - \frac{\cosh (λ_{i}) + \cos (λ_{i})}{\sinh (λ_{i}) + \sin (λ_{i})} [s i n h (λ_{i} \frac{x}{L}) - s i n (λ_{i} \frac{x}{L})],

i = 1,2, \dots, n,

where $λ_{i}$ is obtained from the following characteristic equation:

24

1 + c o s h (λ_{i}) c o s (λ_{i}) = 0 \begin{array}{l} , i = 1,2, \dots, n . \end{array}

Lagrange’s equation is written as:

25

\frac{d}{d t} (\frac{\partial l}{\partial \dot{η}}) - \frac{\partial l}{\partial η} = F, l = K - U, η = (χ, q) .

Substituting the energy expressions into Eq. (25), the equation of motion of the whole structural system is gotten:

26

[M] \{\ddot{d}\} + [C] \{\dot{d}\} + [K] \{d\} + \{Q\} + [F] \{V (t)\} = 0,

where:

[M] = [\begin{matrix} [M_{χ χ}] & 0 \\ 0 & [M_{q q}] \end{matrix}], [C] = [\begin{matrix} 0 & [C_{χ q}] \\ [C_{q χ}] & [C_{q q}] \end{matrix}], [K] = [\begin{array}{l} [K_{χ χ}] & [K_{χ q}] \\ [K_{q χ}] & [K_{q q}] \end{array}], \{Q\} = \{\begin{array}{l} \{Q_{χ}\} \\ \{Q_{q}\} \end{array}\},

[F] = [\begin{array}{l} [F_{χ}] \\ [F_{q}] \end{array}], \{V (t)\} = {\{\begin{array}{l} V_{1} (t) & \dots & V_{N_{p}} (t) \end{array}\}}^{T}, \{d\} = \{\begin{array}{l} {\{χ\}}^{T} \\ {\{q\}}^{T} \end{array}\} .

The expressions of these matrices are listed in the Appendix. Eq. (26) characterizes the piezoelectric actuators driven under the external applied voltages $\{V (t)\}$ . The state-space formulation of Eq. (26) is given as:

27

\{\dot{η}\} = [\bar{A}] \{η\} + [\bar{B}] \{V (t)\} + [\bar{F}],

where:

\{η\} = \{\begin{array}{l} \{d\} \\ \{\dot{d}\} \end{array}\}, [\bar{A}] = [\begin{matrix} 0 & [I] \\ - {[M]}^{- 1} [K] & - {[M]}^{- 1} [C] \end{matrix}],

[\bar{B}] = [\begin{matrix} 0 \\ - {[M]}^{- 1} [F] \end{matrix}], [\bar{F}] = [\begin{matrix} 0 \\ - {[M]}^{- 1} [Q] \end{matrix}] .

3. Active vibration control

A linear classical optimal control algorithm with displacement-velocity feedback is used to determine the control voltage. The cost function to be minimized is given by:

28

J = \int_{0}^{\infty} ({\{\bar{y}\}}^{T} [\bar{Q}] \{\bar{y}\} + {\{u\}}^{T} [\bar{R}] \{u\}),

where:

29

\{\bar{y}\} = [{\bar{C}}_{0}] \{η\},

is the output equation and $[{\bar{C}}_{0}]$ is the output matrix. $[\bar{Q}]$ and $[\bar{R}]$ are the semi-positive-definite and positive-definite weighting matrices on the outputs and control inputs respectively. Assuming full state feedback, the control law is given by:

30

\{u\} = - [G] \{η\},

where $[G]$ is the control gain given by:

31

[G] = \frac{1}{2} {[\bar{R}]}^{- 1} {[\bar{B}]}^{T} [P] .

$[P]$ satisfies the Riccati equation [12]:

32

[P] [\bar{A}] - \frac{1}{2} [P] [\bar{B}] {[\bar{R}]}^{- 1} {[\bar{B}]}^{T} [P] + {[\bar{A}]}^{T} [P] + 2 [\bar{Q}] = 0 .

Substituting Eq. (30) into Eq. (27) leads to:

33

\{\dot{η}\} = ([\bar{A}] - [\bar{B}] [G]) \{η\} + [\bar{F}] .

The controlled response of the system can be gotten by solving Eq. (33).

4. Numerical simulation

In this section, several numerical examples are presented to evaluate the active control of rotating beam with moving mass. The material of the beam is steel, which $E =$ 209 GPa, $ρ =$ 7800 kg/m³. The piezoelectric material is PZT-5H, which $c_{11} =$ 49 GPa, $ρ_{p} =$ 7500 kg/m³, $e_{31} =$ –6.5 C/ m², and $\in_{33} =$ 1.3×10-8 F/m.

First, the concentrated mass travelling on the rotating simply supported beam is considered. The dimensions of the system are $L =$ 2 m, $L_{p} =$ 0.1 m, $b =$ 0.03 m, $h =$ 0.01 m, $h_{p} =$ 0.005 m. The moving mass is $m =$ 0.4 kg. Six piezoelectric patches have been considered to be attached on the bottom surface of the beam. Their locations are $x_{1} =$ 0.4 m, $x_{2} =$ 0.6 m, $x_{3} =$ 0.85 m, $x_{4} =$ 1.05 m, $x_{5} =$ 1.3 m, $x_{6} =$ 1.5 m. The initial conditions are: $L_{m} (0) =$ 0, $θ (0) =$ 0. The rotational speed of the beam is $\dot{θ} =$ 0.09 $π$ rad/s, and the travelling speed of the moving mass is $v =$ 0.4 m/s. The matrix $[\bar{Q}]$ and $[\bar{R}]$ are given as follows:

[\bar{Q}] = [\begin{array}{l} [Q_{1}] \\ [Q_{2}] \end{array}], [\bar{R}] = 0.005 \cdot {[I]}_{N_{p} \times N_{p}},

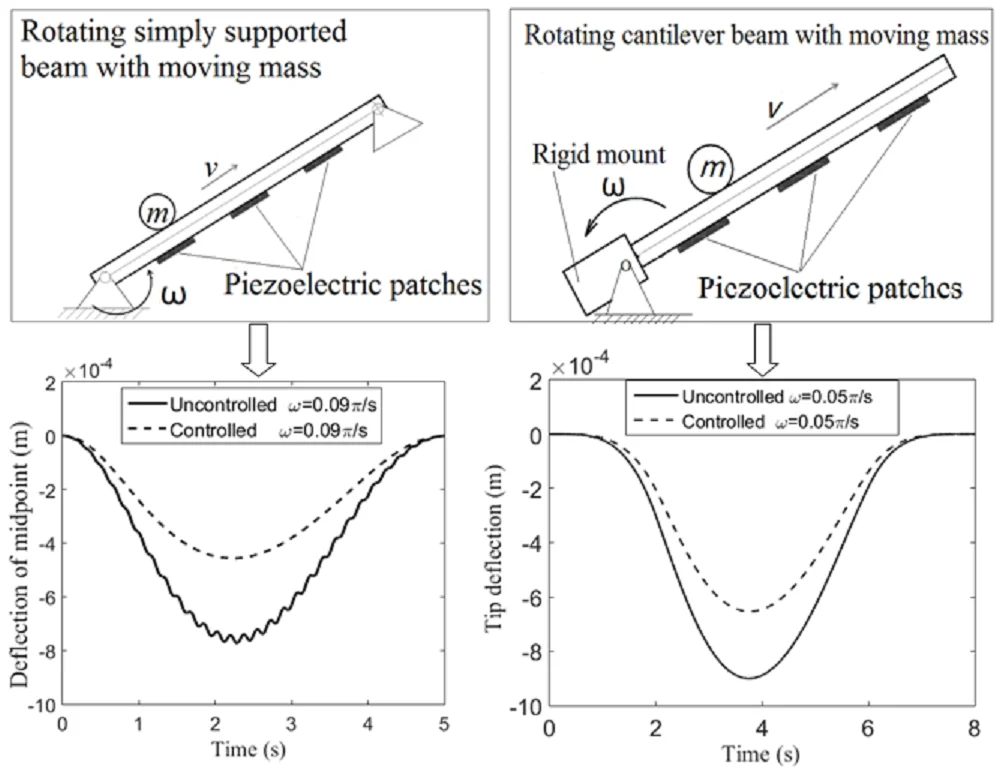
where $[Q_{1}] = 1 \times 1 0^{- 11} \cdot {[I]}_{2 n \times 2 n}$ , $[Q_{2}] = 3 \times 1 0^{11} \cdot {[I]}_{2 n \times 2 n}$ , and $[I]$ is diagonal matrix. Fig. 3 shows the transverse displacement of midpoint ( $w_{m}$ ) of the rotating simply supported beam. For comparison, the responses when the beam does not rotate ( $\dot{θ} =$ 0) are also given. It can be observed from Fig. 3 that the transverse displacements of the beam are reduced significantly by the actuators. When the beam rotates, the transverse component of gravity of the moving mass decreases. Thereby, it can be seen clearly from Fig. 3 that the deflection of the beam is smaller when it rotates than it does not. The required control voltages for the piezoelectric patches (p1-p6) under different rotational speed are shown in Fig. 4. We can find that larger rotational speed results in smaller control voltage.

Fig. 3Transverse displacements of the rotating simply supported beam

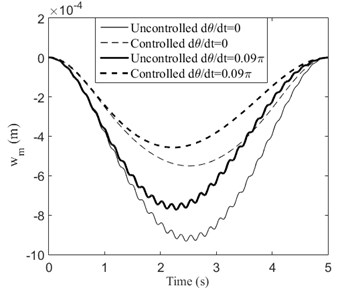
Fig. 4Control voltage of each piezoelectric patch for the rotating simply supported beam

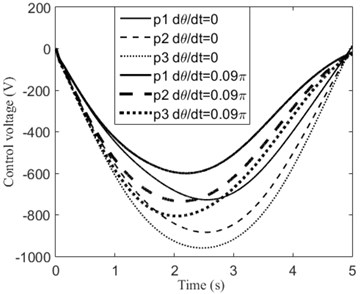
a)

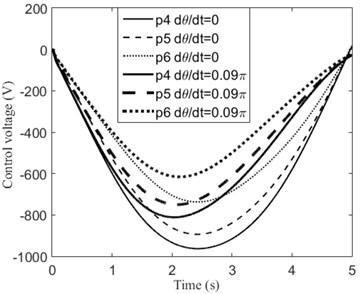
b)

The moving mass moves with variable speed is also considered. The movement rule of the system is given as follows:

At the beginning, $L_{m} =$ 0, $v =$ 0, $θ =$ 0;

When 0 $\leq t \leq$ 2, $v = 0.5 t$ , $\dot{v} =$ 0.5m/s², $\dot{θ} =$ 0.05 $π$ rad/s;

When 2 $< t \leq$ 4, $v = 1 - 0.5 (t - 2)$ , $\dot{v} =$ –0.5 m/s², $\dot{θ} =$ 0.05 $π$ rad/s;

When 4 $< t \leq$ 6, $v = - 0.5 (t - 4)$ , $\dot{v} =$ –0.5 m/s², $\dot{θ} =$ 0.05 $π$ rad/s;

When 6 $< t \leq$ 8, $v = - 1 + 0.5 (t - 6)$ , $\dot{v} =$ 0.5 m/s², $\dot{θ} =$ 0.05 $π$ rad/s.

The numerical simulation results are given in Fig. 5. As we expected, the vibration of the beam is suppressed.

Fig. 5When the moving mass moves with variable speed: a) transverse displacement of midpoint of beam, b) control voltage, c) trajectory of the moving mass

When the moving mass moves with variable speed: a) transverse displacement of midpoint of beam, b) control voltage, c) trajectory of the moving mass

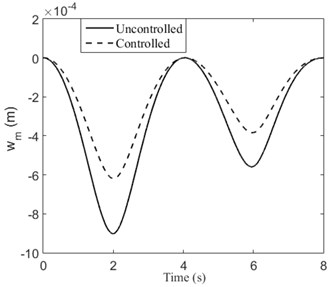
a)

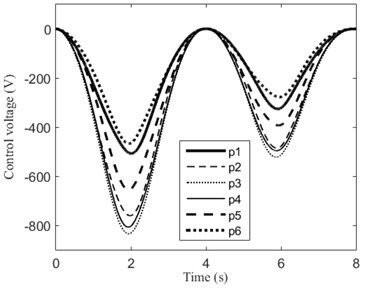
b)

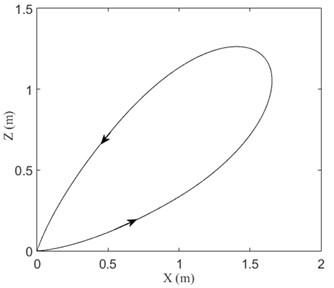
c)

In order to investigate the effect of angular acceleration to the system, two cases are considered: Case 1, $v =$ 0.4 m/s, $\dot{θ} =$ 0.05 $π$ rad/s, $\ddot{θ} =$ 0; Case 2, $\dot{θ} =$ 0, $\ddot{θ} =$ 0.02 $π$ rad/s². The initial conditions are: $L_{m} (0) =$ 0, $θ (0) =$ 0. At the end of time (5 s), the beam has the same angular displacement (0.25 $π$ ) in the two cases. The simulation results are displayed in Fig. 6. It is observed that the beam has larger transverse displacement in Case 2. This is caused by inertial force due to angular acceleration. Obviously, the transverse displacements of the beam are significantly reduced in both cases. The required control voltages for the piezoelectric patches of the two cases are displayed in Fig. 7. We can see that larger control voltages are required in Case 2.

Finally, the concentrated mass travelling on the rotating cantilevered beam is investigated. The length of the beam is $L =$ 1 m. Other dimensions of the system are the same as the rotating simply supported beam. Three piezoelectric patches are used in this studying and their locations are $x_{1} =$ 0, $x_{2} =$ 0.2 m, $x_{3} =$ 0.4 m. The movement rule of the system is given as follows:

At the beginning, $L_{m} =$ 0, $v =$ 0, $θ =$ 0;

When 0 $\leq t \leq$ 2, $v = 0.25 t$ , $\dot{v} =$ 0.25 m/s², $\dot{θ} =$ 0.05 $π$ rad/s;

When 2 $< t \leq$ 4, $v = 0.5 - 0.25 (t - 2)$ , $\dot{v} =$ –0.25 m/s², $\dot{θ} =$ 0.05 $π$ rad/s;

When 4 $< t \leq$ 6, $v = - 0.25 (t - 4)$ , $\dot{v} =$ –0.25 m/s², $\dot{θ} =$ 0.05 $π$ rad/s;

When 6 $< t \leq$ 8, $v = - 0.5 + 0.25 (t - 6)$ , $\dot{v} =$ 0.25 m/s², $\dot{θ} =$ 0.05 $π$ rad/s.

Fig. 6Transverse displacements of Case 1 and Case 2

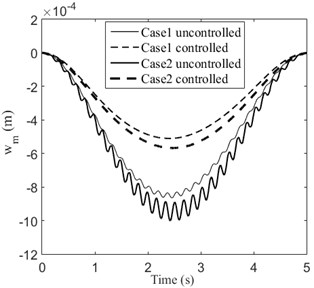
Fig. 7Control voltage of each piezoelectric patch of Case 1 and Case 2

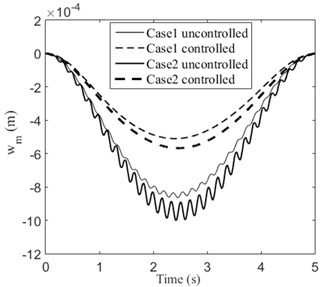
a)

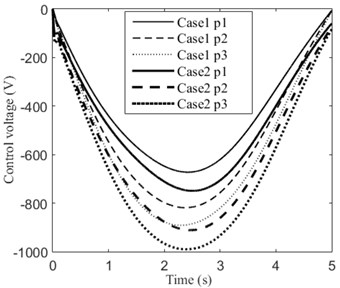
b)

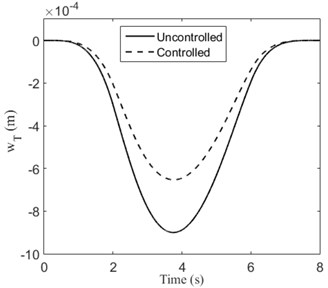
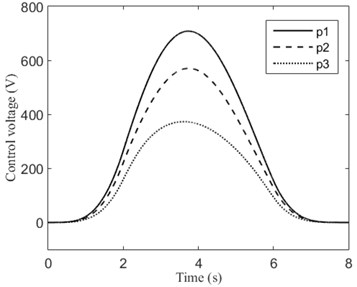
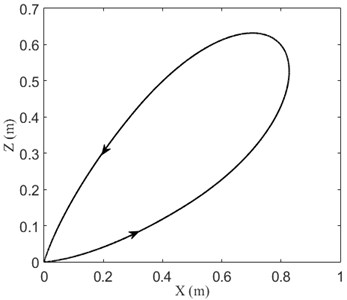
The matrix $[\bar{Q}]$ and $[\bar{R}]$ are the same as in the previous examples. We can observe from Fig. 8 that the transverse displacements are reduced significantly, where $w_{T}$ denotes the tip deflection of the beam. The trajectory of the moving mass is shown in Fig. 9.

Fig. 8Tip displacements and control voltages of the rotating cantilevered beam

a)

b)

Fig. 9Trajectory of the moving mass when v= 0.2 m/s, θ˙= 0.05π rad/s

5. Conclusions

In present paper, active vibration control of rotating beam with moving mass using piezoelectric actuator is investigated. Rotating simply supported beam and cantilevered beam are considered in our studying. The equations of the system are derived by Lagrange’s equation with the assumed mode method. The linear classical optimal control algorithm with displacement-velocity feedback is used to determine the control voltage.

Some numerical examples are employed to evaluate the control performances. It is found that the vibration of the beam can be effectively reduced by the actuators both for rotating simply supported beam and cantilevered beam. Moreover, larger rotational speed results in smaller deflection and control voltage. When there is a uniform angular acceleration, larger vibration amplitudes are gotten. This is caused by inertial force due to angular acceleration.

References

Sun B., Huang D. Vibration suppression of laminated composite beams with a piezoelectric damping layer. Composite Structures, Vol. 53, Issue 4, 2001, p. 437-447.

Publisher
Chen L. W., Lin C. Y., Wang C. C. Dynamic stability analysis and control of a composite beam with piezoelectric layers. Composite Structures, Vol. 56, Issue 1, 2002, p. 97-109.

Publisher
Lin J. C., Nien M. H. Adaptive control of a composite cantilever beam with piezoelectric damping-modal actuators/sensors. Composite Structures, Vol. 70, Issue 2, 2005, p. 170-176.

Publisher
Qiu Z. C., Zhang X. M., Wu H. X., Zhang H. H. Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate. Journal of Sound and Vibration, Vol. 301, Issues 3-5, 2007, p. 521-543.

Publisher
Kumar K. R., Narayanan S. Active vibration control of beams with optimal placement of piezoelectric sensor/actuator pairs. Smart Materials and Structures, Vol. 17, Issue 5, 2008, p. 055008.

Publisher
Song Z. G., Li F. M. Active aeroelastic flutter analysis and vibration control of supersonic beams using the piezoelectric actuator/sensor pairs. Smart Materials and Structures, Vol. 20, 2011, p. 055013.

Publisher
Raja S., Prathap G., Sinha, P. K. Active vibration control of composite sandwich beams with piezoelectric extension-bending and shear actuators. Smart Materials and Structures, Vol. 11, Issue 1, 2002, p. 63-71.

Publisher
Hu Y. R., Ng A. Active robust vibration control of flexible structures. Journal of Sound and Vibration, Vol. 288, Issues 1-2, 2005, p. 43-56.

Publisher
Sung Y. G. Modelling and control with Piezo-Actuators for a simply supported beam under a moving mass. Journal of Sound and vibration, Vol. 250, Issue 4, 2002, p. 617-626.

Publisher
Nikkhoo A., Rofooeia F. R., Shadnam M. R. Dynamic behavior and modal control of beams under moving mass. Journal of Sound and Vibration, Vol. 306, Issues 3-5, 2007, p. 712-724.

Publisher
Nikkhoo A., Amankhani M., Ghafari H. Vibration suppression in smart thin beams with piezoelectric actuators under a moving load/mass accounting for large deflections of the base structure. Indian Journal of Science and Technology, Vol. 7, Issue 2, 2014, p. 211-220.

Publisher
Rofooei F. R., Nikkhoo A. Application of active piezoelectric patches in controlling the dynamic response of a thin rectangular plate under a moving mass. International Journal of Solids and Structures, Vol. 46, Issues 11-12, 2009, p. 2429-2443.

Publisher
Lin Y. H., Trethewey W. M. Active vibration suppresion of beam structures subjected to moving loads: A feasibility study using finite elements. Journal of Sound and Vibration, Vol. 166, Issue 3, 1993, p. 383-395.

Publisher
Ryu B. J., Kong Y. S. Dynamic Responses and Active Vibration Control of Beam Structures under a Travelling Mass. Intech Publisher, 2012.

Publisher
Esmailzadeh E., Ghorashi M. Vibration analysis of beams traversed by uniform partially distributed moving masses. Journal of Sound and Vibration, Vol. 184, Issue 1, 1995, p. 9-17.

Publisher
Michaltsos G., Sophianopoulos D., Kounadis A. N. The effect of a moving mass and other parameters on the dynamic response of a simply supported beam. Journal of Sound and Vibration, Vol. 191, Issue 3, 1996, p. 357-362.

Publisher
Esmailzadeh E., Ghorashi M. Vibration analysis of a Timoshenko beam subjected to a travelling mass. Journal of Sound and Vibration, Vol. 199, Issue 4, 1997, p. 615-628.

Publisher
Mofid M., Shadnam M. On the response of beams with internal hinges, under moving mass. Advances in Engineering Software, Vol. 31, Issue 5, 2000, p. 323-328.

Publisher
Wu J. J. Dynamic analysis of an inclined beam due to moving loads. Journal of Sound and Vibration, Vol. 288, Issues 1-2, 2005, p. 107-131.

Publisher

Cited by

Dynamic Stability and Response of Inclined Beams Under Moving Mass and Follower Force

D. S. Yang | C. M. Wang | J. D. Yau

(2020)

About this article

Received

09 June 2018

Accepted

22 January 2019

Published

15 August 2019

SUBJECTS

Vibration generation and control

DOI

https://doi.org/10.21595/jve.2019.20017

Keywords

rotating beam

moving mass

active control

piezoelectric actuator

Acknowledgements

This work was funded by the Shanghai Education Commission Project for Academic Degree Construction and Research on Industrial Robot Applications under Project No. 230001-17-13.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2018 10 19

Adaptive vibration control for a cantilevered beam using actuating and sensing functions of a piezoelectric bimorph

Ruiping Wang, Ting Zhang, Yue Yang

Research article

2018 02 15

Vibration control of rotating piezo-composite blade beam with CUS configuration based on optimal LQG controller

Tingrui Liu, Guifang Liu

Research article

2017 12 31

Active vibration isolation using a six-axis orthogonal vibration isolation platform with piezoelectric actuators

Shuai Wang, Zhaobo Chen, Yinghou Jiao, Xiaoxiang Liu

Review article

2017 08 15

Invited Review: Recent developments in vibration control of building and bridge structures

Khaled Ghaedi, Zainah Ibrahim, Hojjat Adeli, Ahad Javanmardi

L. Zhao and Y.-P. Wu, “Active vibration control of rotating beam with moving mass using piezoelectric actuator,” Journal of Vibroengineering, Vol. 21, No. 5, pp. 1330–1341, Aug. 2019, https://doi.org/10.21595/jve.2019.20017

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2019.20017
UR  - https://doi.org/10.21595/jve.2019.20017
TI  - Active vibration control of rotating beam with moving mass using piezoelectric actuator
T2  - Journal of Vibroengineering
AU  - Zhao, Liang
AU  - Wu, Yu-Ping
PY  - 2019
DA  - 2019/08/15
PB  - JVE International Ltd.
SP  - 1330-1341
IS  - 5
VL  - 21
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhao_2019,
	doi = {10.21595/jve.2019.20017},
	url = {https://doi.org/10.21595/jve.2019.20017},
	year = 2019,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	number = {5},
	pages = {1330--1341},
	author = {Liang Zhao and Yu-Ping Wu},
	title = {Active vibration control of rotating beam with moving mass using piezoelectric actuator},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]L. Zhao and Y.-P. Wu, “Active vibration control of rotating beam with moving mass using piezoelectric actuator,” Journal of Vibroengineering, vol. 21, no. 5, pp. 1330–1341, Aug. 2019, doi: 10.21595/jve.2019.20017.

Copy IEEE

Copied to clipboard!

Zhao, Liang, and Yu-Ping Wu. “Active Vibration Control of Rotating Beam with Moving Mass Using Piezoelectric Actuator.” Journal of Vibroengineering 21, no. 5 (August 15, 2019): 1330–41. https://doi.org/10.21595/jve.2019.20017.

Copy Chicago

Copied to clipboard!

Active vibration control of rotating beam with moving mass using piezoelectric actuator

Abstract

Highlights

1. Introduction

2. Formulation of the equations of motion

3. Active vibration control

4. Numerical simulation

5. Conclusions

References

Cited by

About this article

Related Articles