Bearing degradation assessment based on entropy with time parameter and fuzzy c-means clustering

2.1. Wavelet packet decomposition

Wavelet packet decomposition is also called subband tree or optimal subband tree structuring. It uses parse tree to indicate wavelet packet. Wavelet transform is a popular method to process non-stationary signals [17, 18]. Comparing with short time Fourier transform, it can reduce computations when examining specific frequencies and giving a flexible time-frequency domain feature because of the use of variable sized windows. However, wavelet transform only decomposes low frequency signals and that leads to reduction of time-frequency resolution with the increase of frequency. Wavelet packet decomposition solves the problem and has a better resolution in high frequency signals. Besides, it draws into the concept of optimal basis selection to select optimal basis function flexibly. The process of wavelet packet decomposition is as follows [19].

Assume that ${\phi }_0\left(x\right)$ is scaling function and ${\phi }_1\left(x\right)$ is wavelet function. The basic wavelet packet functions are defined as:

where $h\left(k\right)$ and $g\left(k\right)$ are the quadrature mirror filters.

For a discrete signal, the decomposition coefficients of wavelet packets can be computed iteratively by:

where ${\mathbf{{\rm X}}}_{n,j}^{}$ denotes the wavelet coefficients at the $j$ level, $n$ subband and $m$ is the number of the wavelet coefficients.

Fig. 1An example of a three-level wavelet packet decomposition tree

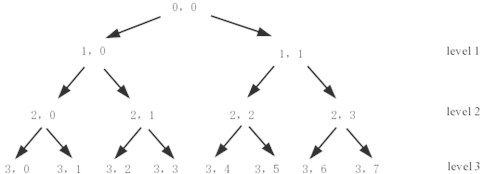
From Eqs. (2), (3), signals can be decomposed into level $j$ and the level $j$ will get ${\text{2}}^j$ part of signals by frequency. For example, a wavelet packet decomposition tree of three levels is illustrated in Fig. 1.

2.2. Auto regressive (AR) model spectrum

Auto regressive model is one of the most widely used and discussed parameter models. Auto regressive model spectrum consists of two steps. One is building AR model for time domain signals. The other is calculating the power spectrum by model coefficient [20]. The AR model is defined as:

where ${\phi }_1$, …, ${\phi }_p$ are the parameters of the model, $c$ is a constant, and ${\epsilon }_t$ is white noise.

Eq. (3) can be regarded as an input or output equation to a system. Single side spectrum of signals can be calculated by transfer function:

where ${\sigma }_Z^2=Var\left(Z_t\right)$. In this paper, every subband will be reconstructed by AR model spectrum, and the details of subband can be more entire [21].

2.3. Entropy with time parameter

In information theory, entropy is the probability of discrete random evens and is sometimes referred to as Shannon entropy. In other words, the entropy increases as the certainty of variable increases and the information to understand will increase. Then, the signals of healthy bearing will provide orderly and steady information. When the bearing is running to failure, the system of bearing will be unsteady, and the signals will provide unordered and chaotic information. Entropy can perform the condition of information in the degradation process of bearing. It is a fine index to describe the degradation state. Entropy is defined as:

where $p_i$ is the probability of a discrete set [22].

From Eq. (5), the energy of every subband can be calculated. If the energy of $i$ subband is $E_i$, $p_i$ is defined as:

At the beginning of operation, the bearing has to work in a wear-in period. That can lead to the fluctuation of entropy in initial stage. To solve the problem, this paper put up with the time parameter which is used to reflect the wear of bearing accumulated over time. The range of time parameter should be between 0 and 1 in order to control the degradation index. Assuming that there are $N$ samples in a whole life of the bearing, the time parameter ($tp$) of the $n$th set of data is:

where $t$ is the time of each sample. The parameter is also a dimensionless parameter. That means it is more objective to reflect the rule of bearing degradation. Then, a new indicator, entropy with time parameter ($Htp$) can be calculated in Eq. (8) as:

2.4. Fuzzy clustering

Clustering is the task of grouping a set of objects in such a way that objects in the same group are more similar to each other than to those in other groups. Fuzzy clustering is always used in the classification when things are blurring. To divide the process of degradation, fuzzy clustering is an ideal method based on fuzzy mathematics [7].

Fuzzy c-means (FCM) is a commonly used algorithm in fuzzy clustering. The FCM algorithm attempts to partition a finite collection $X=\left\{x_1,x_2,\dots ,x_n\right\}$. Clustering loss function based on membership function is defined as:

where ${\mu }_j\left(x_i\right)$ is membership function, $c_j$ is the center of the $j$th cluster of $k$ clusters, $m$ is smoothing parameter, and $\sum _{j=1}^k{\mu }_j\left(x_i\right)=$ 1. Then, using Lagrange multiplier method to find the $\mu$ and $c$, which make $J$ get lowest. When the algorithm converges, the fuzzy clustering will finish [23].

In this paper, $Htp$ is used as the finite collection to divide stages. The time and threshold of the last stage can be regarded as the warn of bearing failure. Flowchart is shown in Fig. 2.

Fig. 2Procedure of signal processing and bearing assessment

3.1. Feature extraction

The bearing run-to-failure data used at this session have been obtained from FEMTO-ST Institute and Intelligent Maintenance System Center (IMS). In the experiment of FEMTO-ST Institute, the load is applied to the bearing radially in horizontal direction. Its vibration signal data is collected at a sampling frequency of 25.6 kHz every 10 s for 0.1 s. When the acceleration amplitude exceeds the threshold of 20, the bearing is considered failure. This paper uses the six groups of run-to-failure data and the operation condition is shown in Table 1.

Taking bearing 1-2 as an example, use WPD to decompose the vibration signal into 8 subband at first. And the energy of each subband will be obtained by AR model spectrum analysis, which is shown in Fig. 3.

Fig. 3Energy of 8 subband

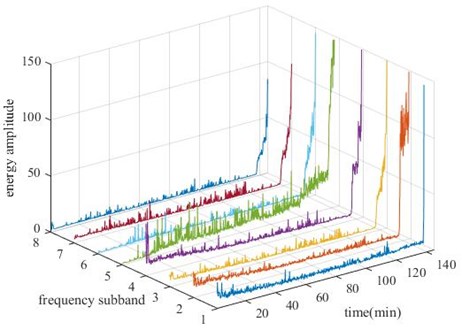
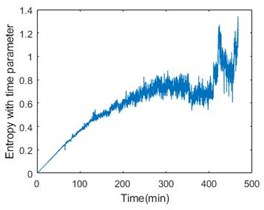
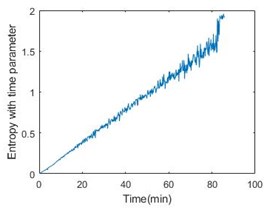
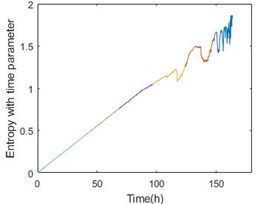
Fig. 4Entropy with time parameter of 6 bearings

a)

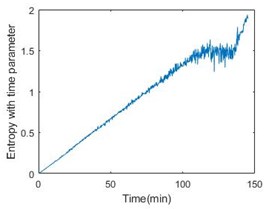
b)

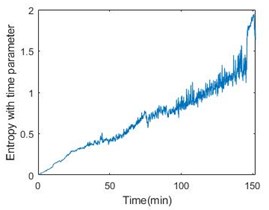
c)

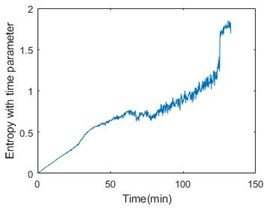
d)

e)

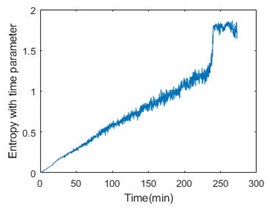
f)

Then, calculate the entropy according to Eq. (6) and it is shown in Fig. 3, from which it is obvious that the bearing is not stable at the beginning of operation. Introducing the time parameter will make the feature more effective. The feature of six bearings is shown in Fig. 4.

3.2. Degradation process evaluation

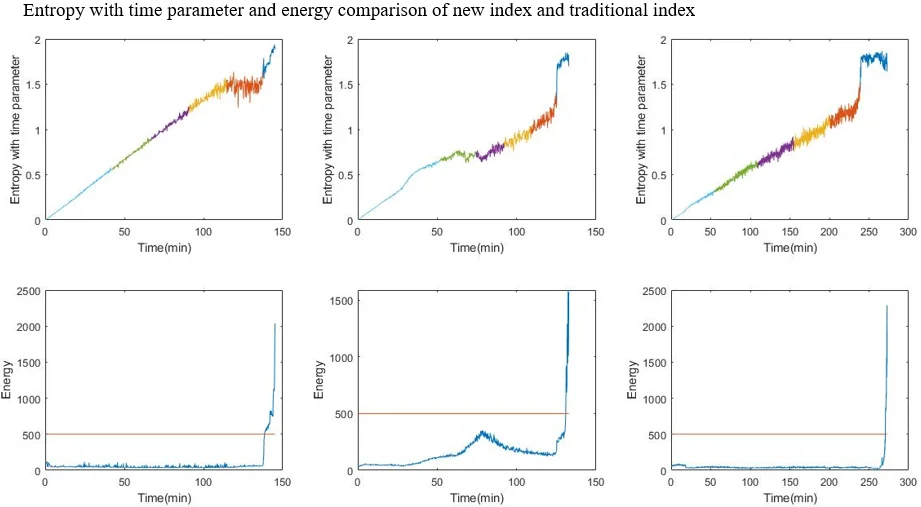
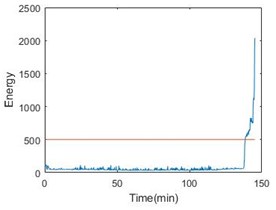
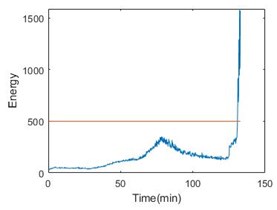
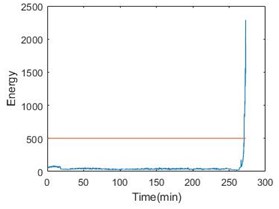
Since the entropy with time parameter has been obtained, fuzzy c-means clustering can be used to estimate the state of bearings. In this paper, it is appropriate to divide the operation into 6 stages. Taking bearing 1-2, bearing 2-2 and bearing 3-2 as examples, Fig. 5 gives the result of clustering.

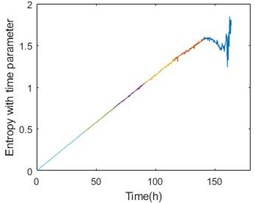
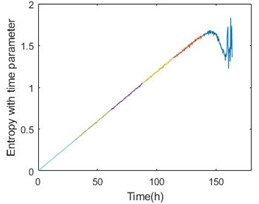
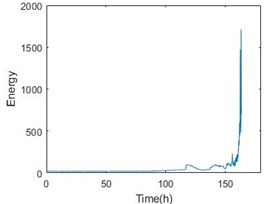
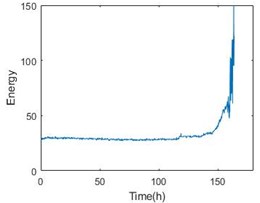
Fig. 5 also gives energy of the bearing. From the comparison, the stage can perform the degradation process. More importantly, the last stage will become a nice warning of bearing failure. Table 2 shows the details of all the six bearings. From the table, the threshold time is less than 15 % ahead of failure time.

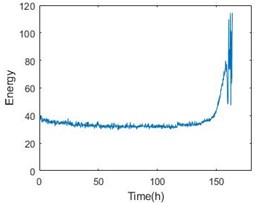
To confirm the effectiveness of the method, the paper also adopts the data from IMS. The experiment of IMS provide the vibration data at a sampling frequency of 20 kHz every 10 min for 1 s in No.2 set. In the set, there are 4 bearings working in 2000 rpm and a load of 6000 lbs for about 163 h. The result is shown in Fig. 6 and Table 3. The threshold time is also less than 15 % ahead of failure time. Obviously, the method of degradation evaluation has good universality.

Fig. 5Entropy with time parameter and energy comparison of the 3 bearings

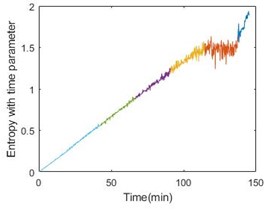
a)

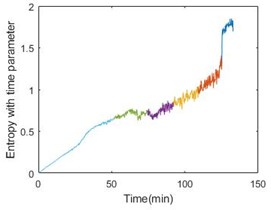
b)

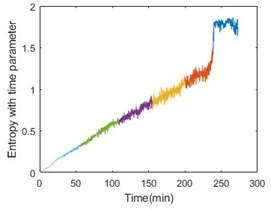
c)

d)

e)

f)

Fig. 6Entropy with time parameter and energy comparison of the 1-3 bearing

a)

b)

c)

d)

e)

f)