Abstract
The key to the evaluation of bearing performance degradation is to extract sensitive characteristic indicators that can reflect the degradation process. In order to solve the problem of insufficient sensitivity of the bearing multi-source signals feature, a fusion entropy ratio feature based on dynamic time warping is proposed. First, the segmented approximate entropy, sample entropy and fuzzy entropy of the bearing performance degradation process are extracted, and then the mean clustering is used to obtain the standard entropy vector of the health state. In order to eliminate the influence of working environment and entropy value on state evaluation, a concept of entropy ratio is defined by the ratio of the entropy vector of each state to the standard entropy vector of the health state. Finally, using dynamic time warping has the advantage of accurately describing the similarity between vectors from a global perspective, and the multi-source heterogeneous fusion entropy ratio distance feature is constructed to describe the degraded state of bearing performance. Experiments show that this feature is more sensitive to the bearing performance degradation than other features, such as fusion entropy ratio feature based on Euclidean distance, single entropy ratio feature based on dynamic time bending.
1. Introduction
The key to accurate evaluation of machinery equipment’s state is to find sensitive indicators that reflect the degradation process. The most common way to construct performance degradation indicators is to extract root mean square, cliffness, wavelet energy, etc. [1-3], but it is difficult to install sensors in the narrow space, so the common method is to find the bearing status by monitoring the signal far away from the vibration source [4]. The development of artificial intelligence has led to an increasing number of studies using advanced algorithms such as genetic coding, neural networks, and deep learning for bearing service performance evaluation [5-7]. In the construction of information fusion evaluation index, since many physical quantities such as oil granularity and temperature do not have parameters of characteristic frequency, multiple information entropies are commonly used to construct feature values [8-9], but these literatures generally construct entropy improvement features based on single physical quantity signals, and do not consider the fusion of multi-source heterogeneous signals. In this paper, we propose a multi-source heterogeneous fusion entropy ratio distance feature based on dynamic time bending for bearing performance degradation.
2. Entropy characterization of multi-source heterogeneous physical quantity of bearing performance degradation state
Entropy is often used as a quantitative measure of the information content in a system, characterizing the probability of occurrence of information embedded in a time series. If the probability of an event occurring is , then entropy is defined as:
The Eq. (1), entropy is a function of the probability distribution about the variable , the probability of taking the negative logarithm indicates the amount of information carried out when a possible event occurs. There are many types of information entropy, such as approximate entropy, sample entropy, fuzzy entropy, permutation entropy and so on. Suppose the vibration, strain and axial force signals of a bearing are monitored, and its approximate entropy, sample entropy and fuzzy entropy are extracted respectively, and define , and as the vibration entropy vector, strain entropy vector and axial force entropy vector, then:
Using these entropy vectors, a multi-source heterogeneous entropy characteristic matrix that can characterize the degradation state of the bearing performance is constructed as follows:
3. Multi-source fusion entropy ratio feature algorithm based on dynamic time bending
Assume bearing status data are sampled at 1 second intervals, and points are sampled in one sampling period. Assuming that the bearings are in a healthy state during the first seconds, extract the multi-type entropy values of these multi-source physical quantities, and construct multi-source heterogeneous fusion features, and then the healthy standard entropy features are obtained by mean clustering as follows:
In the multi-source heterogeneous vector, each physical quantity eigenvalue has a large difference between different physical quantities despite the fluctuation, and the entropy ratio characteristic is that each entropy in the vector is divided by the corresponding healthy standard entropy, defined as , and the multi-source heterogeneous fusion entropy ratio characteristic at the moment of as follows:
At this time, the entropy ratio features of the health state are all 1 vectors. As the monitoring time advances, each sampling moment can form the entropy ratio feature of this moment, which is equivalent to the probability of occurrence of the dimensionless feature after removing the initial health condition.
The dynamic time warping (DTW) [10-11], has been proved to be an extremely strong distance metric for time series, whose main idea is to adjust the correspondence between time points and guide to find the best matching path between data in two arbitrary long time series, which can effectively avoid the Euclidean distance mismatch caused by the response time delay between different physical quantities.
It is assumed there are two feature vectors and , which form the distance between the data points of the two sequences, where , ., , then DTW is to find a continuous path from this matrix such that the sum of the element values on the path is minimal and the three conditions of boundary restriction, continuity and monotonicity are satisfied. The path can be implemented by dynamic programming by defining the accumulation matrix as the shortest path from the starting position to the ending position, then we have:
The DTW can be obtained as:
DTW describes the closest distance between all feature points, so it can describe the similarity of two vectors more accurately, and also can solve the problem of inconsistent length between two variables. According to the above analysis, Our algorithm steps are as follows:
Step 1: Collect the multi-physical quantity monitoring data of the whole life cycle of bearing operation, here it is assumed that the sampling is vibration, strain and stress data, i.e. , the data is pre-processed, and the bearing status is divided into four stages of healthy state, early fault, mid-term fault and late fault by observation.
Step 2: Extract the approximate entropy, sample entropy and fuzzy entropy of the healthy stage of the bearing, construct a multi-source fusion entropy feature vector , obtain the standard entropy of the health state by mean clustering .
Step 3: Calculate the multi-source fusion entropy vector for each period, and compare it with the health state standard entropy to get the entropy ratio feature , and the health state entropy ratio standard feature is defined as the all-1 feature.
Step 4: According to Eq. (7), DTW distance between the multi-source heterogeneous fusion entropy ratio of each time period and the health state entropy ratio standard feature is calculated, and the multi-source heterogeneous fusion entropy ratio distance feature of each time period is obtained.
To compare the sensitivity of the features, two sensitivity evaluation functions, interval slope and interval maximum magnitude ratio, are proposed, assuming that the slope of the -th feature stage interval can be expressed as the ratio of the difference between the maximum and minimum values in the interval to the length of time, and the maximum magnitude ratio of the -th interval is expressed as the ratio between the maximum and minimum values in the interval.
4. Service performance evaluation experiment in the process of bearing oil cut-off
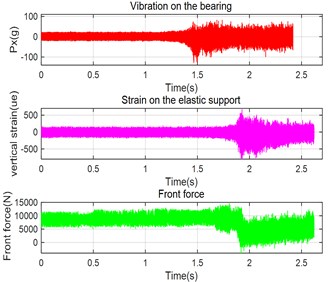
The main bearing of aero-engine is a high-speed bearing, the maximum speed can be more than 30,000 r/min, which often adopts the elastic support structure, as shown in Fig. 1, and the monitoring data are the vibration at the bearing position, the strain at the patch position and the axial force, as shown in Fig. 2. The main bearing is ultimately t inner ring, outer ring and rolling body all failed. The sampling frequency is 10000 Hz, the sampling time vibration is 2.4718 seconds, the strain, the front force is 2.6210 seconds, the first 2.4 seconds are taken as the analysis data. The analysis data were divided into 80 equal segments, and each segment are 0.03 seconds. The approximate entropy, sample entropy and fuzzy entropy of each segment were calculated separately, and the segmented entropy and normalized entropy change graphs were obtained as shown in Fig. 3.
Fig. 1Elastic support for main bearings

Fig. 2Vibration, strain, and forward force monitoring data after bearing oil cut-off
From Fig. 3, it is clear that the vibration entropy gradually increases from the 38th paragraph to the 49th paragraph and then oscillates at a high level; the stress entropy and the front axial force entropy both increase continuously from about the 50th paragraph to the 64th paragraph and reach the maximum, the stress entropy oscillates lower and the front axial force entropy diverges. From the response of vibration, strain and axial force, the changes of all three entropies are relatively consistent, but the vibration response is the most sensitive, and the axial force response of strain is delayed for a period of time.
Fig. 3a) Three entropy and b) normalized entropy for vibration, strain, and forward axial force
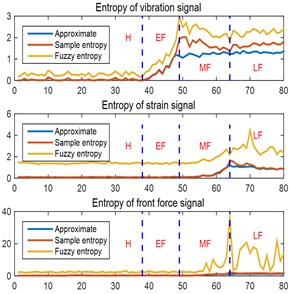
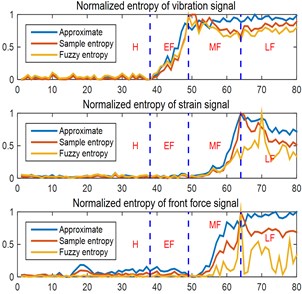
Fig. 4a) The change of fusion entropy and b) entropy ratio during performance degradation
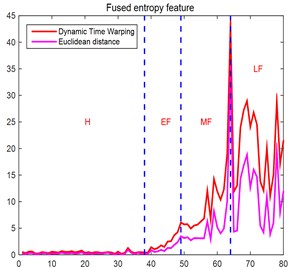
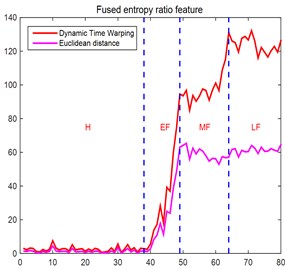
Table 1Multi-source fusion entropy and entropy ratio based on ED to reaction of the fault stage
Early fault | Mid-term fault | ||
Fusion entropy | Interval amplitude ratio | 19.01 | 12.63 |
Interval slope | 10.29 | 57.66 | |
Fusion entropy ratio | Interval amplitude ratio | 56.89 | 0.86 |
Interval slope | 193.69 | –16.09 | |
Table 2Multi-source fusion entropy and entropy ratio based on DTW to reaction of the fault stage
Early fault | Mid-term fault | ||
Fusion entropy | Interval amplitude ratio | 14.64 | 8.75 |
Interval slope | 17.64 | 69.64 | |
Fusion entropy ratio | Interval amplitude ratio | 58.05 | 1.54 |
Interval slope | 287.73 | 83.98 | |
Here extracted characterization of the bearing operating state features vector have vibration, stress, front axial force of each approximate entropy, sample data entropy vector divided by the health benchmark feature vector to get segment entropy ratio vector, and health state benchmark entropy ratio vector of each element can be all set to 1, and then calculate the between each segment entropy ratio vector and health benchmark entropy ratio vector, then get the bearing multi-source heterogeneous fusion entropy ratio distance The curve of feature variation with state is shown in Fig. 4. Here the embedding dimension is taken as 2 and the similarity tolerance is 0.2 times of the entropy standard deviation.
Because the performance degradation is mainly to determine when the degradation occurs and when it is severe enough to fail, it is mainly to discriminate the sensitivity of the eigenvalues of the early and mid--term fault stages, the results are shown in Table 1 and Table 2. The interval amplitude ratio represents the absolute change of the signal feature strength, and the interval slope represents the sensitivity of the signal feature to fault stage. As can be seen from Fig. 4, Table 1 and Table 2, Whether it is early or mid-fault, multi-source heterogeneous fusion entropy ratio feature based on has the greatest sensitivity and feature strength compared with fusion entropy ratio features based on .
Fig. 5The change law of bearing entropy ratio features with the stage of bearing performance degradation
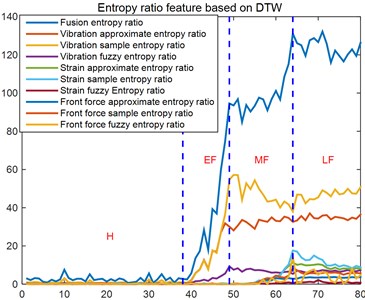
In order to compare the multi-source heterogeneous fusion entropy ratio and the single entropy ratio feature to characterize the performance degradation state of the bearing, the changes of the entropy ratio of 9 single entropy with the bearing performance degradation stage are calculated, as shown in Fig. 5 and Table 3. It can be seen from them, the single entropy ratio of the vibration signal is more sensitive to early faults, but not sensitive to mid-term faults, vibration sample entropy and approximate entropy even show opposite trends. The single entropy ratio of the strain and front force signals have both effects on early fault, and not very sensitive to mid-term fault. In contrast, the interval slope of the multi-source heterogeneous fusion entropy ratio is much larger than other single faults, and it is very sensitive to early and mid-term faults. Based on the above analysis, the multi-source heterogeneous fusion entropy ratio feature proposed in this paper has the strongest ability to characterize the degradation state of bearing performance compare with the single entropy ratio feature.
Table 3Sensitivity of entropy ratio feature to early fault mid-term fault of the bearing
Types of entropy ratio features | Interval slope | Types of entropy ratio features | Interval slope | ||
Early fault | Mid-term fault | Early fault | Mid-term fault | ||
Vibration approximate entropy ratio | 97.21 | 12.43 | Strain fuzzy entropy ratio | 1.43 | 1.65 |
Vibration sample entropy ratio | 168 | –34.55 | Forward force approximate entropy ratio | 1.08 | 5.73 |
Vibration fuzzy entropy ratio | 27.82 | –7.1 | Forward force sample entropy ratio | 1.03 | 15.29 |
Strain approximate entropy ratio | 1.19 | 20.56 | Forward force fuzzy entropy ratio | 1.19 | 26.09 |
Strain sample entropy ratio | 1.19 | 31.91 | Multi-source fusion entropy ratio | 287.73 | 83.98 |
5. Conclusions
The paper proposes a multi-source heterogeneous fusion entropy ratio feature based on DTW, defines a new entropy ratio concept that uses the ratio of the entropy vector of each state of the bearing to the standard entropy vector of the healthy state, and makes innovative use of DTW constructs a multi-source heterogeneous fusion entropy ratio distance that can accurately describe the degradation state of bearing performance. The experiments proves that the multi-source fusion entropy ratio feature based on DTW is more sensitive to the response of bearing performance degradation process, compared with the fusion entropy ratio feature based on Euclidean distance, and the single entropy ratio based on DTW.
References
-
Naipeng Li and Yaguolei, “An improved exponential model for predicting remaining useful life of rolling element bearings,” IEEE Transactions on Industrial Electronics, Vol. 62, No. 12, pp. 7762–7773, Jan. 2015.
-
Z. Huang, Z. Xu, X. Ke, W. Wang, and Y. Sun, “Remaining useful life prediction for an adaptive skew-Wiener process model,” Mechanical Systems and Signal Processing, Vol. 87, pp. 294–306, Mar. 2017, https://doi.org/10.1016/j.ymssp.2016.10.027
-
Z. Huang, Z. Xu, W. Wang, and Y. Sun, “Remaining useful life prediction for a nonlinear heterogeneous wiener process model with an adaptive drift,” IEEE Transactions on Reliability, Vol. 64, No. 2, pp. 687–700, Jun. 2015, https://doi.org/10.1109/tr.2015.2403433
-
L. Liao, “Discovering prognostic features using genetic programming in remaining useful life prediction,” IEEE Transactions on Industrial Electronics, Vol. 61, No. 5, pp. 2464–2472, May 2014, https://doi.org/10.1109/tie.2013.2270212
-
L. Guo, N. Li, F. Jia, Y. Lei, and J. Lin, “A recurrent neural network based health indicator for remaining useful life prediction of bearings,” Neurocomputing, Vol. 240, pp. 98–109, May 2017, https://doi.org/10.1016/j.neucom.2017.02.045
-
L. Liao, W. Jin, and R. Pavel, “Enhanced restricted Boltzmann machine with prognosability regularization for prognostics and health assessment,” IEEE Transactions on Industrial Electronics, Vol. 63, No. 11, pp. 7076–7083, Nov. 2016, https://doi.org/10.1109/tie.2016.2586442
-
P. Boškoski, M. Gašperin, D. Petelin, and Juričić, “Bearing fault prognostics using Rényi entropy based features and Gaussian process models,” Mechanical Systems and Signal Processing, Vol. 52-53, pp. 327–337, Feb. 2015, https://doi.org/10.1016/j.ymssp.2014.07.011
-
K. Zhu, X. Jiang, L. Chen, and H. Li, “Performance degradation assessment of rolling element bearings using improved fuzzy entropy,” Measurement Science Review, Vol. 17, No. 5, pp. 219–225, Oct. 2017, https://doi.org/10.1515/msr-2017-0026
-
G. Zhang, F. Q. Tian, and B. Sh., “Health indicator construction method based on the information entropy of a specific frequency band and the RBM,” Journal of Vibration and Shock, Vol. 39, No. 6, pp. 147–153, 2020.
-
E. Keogh and C. A. Ratanamahatana, “Exact indexing of dynamic time warping,” Knowledge and Information Systems, Vol. 7, No. 3, pp. 358–386, Mar. 2005, https://doi.org/10.1007/s10115-004-0154-9
-
E. J. Keogh and M. J. Pazzani, “Derivative dynamic time warping,” in Proceedings of the 2001 SIAM International Conference on Data Mining, pp. 1–11, Apr. 2001, https://doi.org/10.1137/1.9781611972719.1
About this article
Financial support from Special Research Project on the Key Fields in General Universities of Guangdong Province “Research on Health Monitoring and Intelligent Diagnosis of Main Drive Bearings of Shield Machines” (2020ZDZX2033).
