Research on the oscillation of cooling grills used for terminal devices for voice communication control systems used by air traffic controllers

Korendyasev, George; Asaturov, Mikhail

doi:10.21595/vp.2021.22285

Vibroengineering Procedia

Browse Procedia

Published: 02 December 2021

Check for updates

Research on the oscillation of cooling grills used for terminal devices for voice communication control systems used by air traffic controllers

George Korendyasev¹

Mikhail Asaturov²

¹Mechanical Engineering Research Institute of the Russian Academy of Sciences (IMASH RAN), Moscow, Russia

²Scientific-Production Association Almaz, Moscow, Russia

Corresponding Author:

George Korendyasev

Cite the article Download PDF

Downloads 492

Abstract

During this research, the analytical and numerical oscillation models have been deduced of cooling grills of terminal devices for voice communication control systems used by air traffic controllers. The adequacy of obtained models was verified by a full-scale experiment. Vibration stability of telecommunication terminal cases has high importance for the high-quality reproduction of voice information. Obtained results make it possible to solve two problems at once – problem of reducing heat pressure and of increasing vibration stability of audio reproduction device cases.

1. Introduction

The low noise of the terminal devices is one of the important features of digital voice communication control systems (VCCS) [1] used for air traffic control. The noise rating at the air traffic controller’s workplaces shouldn't be higher than 50 dB. High demands on the reliability of VCCS require certain architecture. The most reliable architecture is a combination of network distributional architecture and decentralized terminal architecture.

This architecture implies that functions of establishing and managing a phone and radio connection (including the processing of voice and signal information) are carried out by individual terminal processors and interface devices involved in that connection. Terminal devices execute a significant amount of calculations, which is a cause of processor-intensive work state of the motherboard of the terminal, which leads to heat releases of approximate 100 W for each terminal. When the temperature rises above 60 °С, processors’ performance drops down, and the chance of hardware failure increases. Therefore, effective cooling is required for the stable functioning of the processor.

The operating life of terminal devices is at least ten years. That fact and a requirement for the low noise level doesn't allow using active devices (such as coolers, thermoelectric coolers, etc.) for cooling terminal processors. Liquid cooling and thermoelectric cooling are unreasonably expensive and unreliable methods. Therefore, passive cooling is the best possible solution for that type of devices.

Passive cooling requires specific constructive features of the cases:

1) aluminum or copper coolers with a big heatsink area;

2) thermal interfaces between parts of the case;

3) thin-shell designs, sometimes constructed from perforated metal plates to create convectional heat exchange with the outside environment.

In terms of design, cases are made as monoblocks, produced from aluminum compositions (Fig. 1). As a result, the whole case of the terminal functions as a cooler.

Fig. 1General view of telecommunication terminal

Such a solution allows getting a larger area of a heatsink and consequently more effective cooling of motherboard processor. The absence of joints in the monoblock device drastically lowers the heat resistance of the case. The perforated grille is used for heat withdrawal (Fig. 1). The total area of the holes provides an effective heat exchange with the external environment.

In order to choose what type of perforation and what sheet thickness has to be applied, two effects must be taken into consideration. Firstly, we need to identify the natural frequencies of perforated sheet parts. Secondly, we have to determine how parameters of perforation and device oscillation frequency influence each other. Natural frequencies of monoblock cases, in general, are higher than the voice channel bandwidth; meanwhile, natural frequencies of delicate elements of the case, such as perforated grill sheets, often get into the vocal range, making noise waves.

Voice frequencies of the 300-3400 Hz bandwidth [2] are used in telephony; however, the frequencies of 20-700 Hz have the greatest impact on the noise immunity of terminal devices. Thus, the fact that natural frequencies mustn't be lower than 700 Hz should be taken into consideration when designing terminal devices.

2. Mathematical model of oscillation

Calculation of a natural frequency of oscillation of vent grills manufactured from perforated sheets is a nontrivial problem. The theoretical basis for calculating the natural frequency of perforated shell oscillation can be found in the article [3-5].

The equation for free transverse oscillations of a model of plates of variable rigidity can be written down as detailed below:

1

D \nabla^{4} ω + \frac{\partial^{2} D}{\partial x^{2}} (\frac{\partial^{2} ω}{\partial x^{2}} + μ \frac{\partial^{2} ω}{\partial y^{2}}) + 2 \frac{\partial D}{\partial x} (\frac{\partial^{3} ω}{\partial x^{3}} + \frac{\partial^{3} ω}{\partial x \partial y^{2}}) + 2 \frac{\partial D}{\partial y} (\frac{\partial^{3} ω}{\partial x^{2} \partial y} + \frac{\partial^{3} ω}{\partial y^{3}}) + \frac{\partial^{2} D}{\partial y^{2}} (\frac{\partial^{2} ω}{\partial y^{2}} + μ \frac{\partial^{2} ω}{\partial x^{2}}) + 2 (1 - μ) \frac{\partial^{2} D}{\partial x \partial y} \frac{\partial^{2} ω}{\partial x \partial y} + \frac{y h}{g} \frac{\partial^{2} ω}{\partial t^{2}} = W = 0,

where $ω$ – the function of normal deflection; $x$ , $y$ – rectangular coordinates, oriented accordingly to sides $a$ and $b$ ; $μ$ – Poisson’s ratio; $h$ – thickness of the plate; $t$ – time; $g$ – free-fall acceleration; $D$ and $γ$ – variable parameters, which characterize bending stiffness and density of equivalent plate – model defined by formulae:

2

D = D_{0} λ, γ = γ_{0} λ, D_{0} = \frac{E_{0} h^{3}}{[12 (1 - μ^{2})]},

where $γ_{0}$ , $E_{0}$ – density and module of elasticity of plate’s material; $λ$ – ratio:

3

λ = 1 + \sum_{i = 1}^{k} \{\sum_{j = 1}^{r} [- Г_{0} (x - x_{1 j i}; y - y_{1 j i}) + Г_{0} (x - x_{2 j i}; y - y_{1 j i})

+ Г_{0} (x - x_{1 j i}; y - y_{2 j i}) - Г_{0} (x - x_{2 j i}; y - y_{2 j i}))],

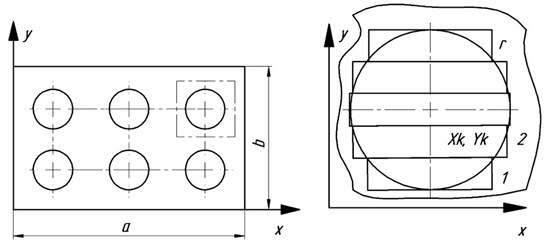
where $k$ – number of oval notches; $r$ – number of rectangular notches by which we approximate the arbitrarily shaped holes, $Г_{0} (x - x_{j i}; y - y_{j i})$ – Heaviside step function [6], $x_{1 i j}$ , $x_{2 i j}$ , $y_{1 i j}$ , $y_{2 i j}$ – coordinates of it’s oval hole (Fig. 2). The function for free transverse oscillations of the rectangular shell, which is fixed along the outline (these boundary conditions describe the attachment of telecommunication terminal vent grills most precisely) is going to be as follows:

4

ω = ω_{1} (x, y) ω (t) = f {s i n}^{2} α x {s i n}^{2} β y s i n ω t,

where $α = m π / a$ , $β = n π / b$ , $m$ , $n$ – number of semi-oscillations forming along $x$ and $y$ axes; $ω$ – main wave circular frequency, $f$ – frequency.

Fig. 2Structural grill design

Taking into account Eq. (1), we have the following formula for a plate oscillation frequency squared:

5

ω^{2} = \frac{64 g D_{0}}{γ_{0} h} \{c_{1}^{*} (S - S_{1}) + \sum_{i = 1}^{k} \sum_{j = 1}^{r} \frac{1}{α β} [- \frac{c}{8} (2 ρ + m_{1 j i} m_{2 j i}) + 2 (1 - μ) α^{2} β^{2} ρ^{*}

+ (α^{4} - ρ^{4}) \bar{ρ} + \frac{с - 4 μ α^{2} β^{2}}{8} m_{1 j i} m_{2 j i} + \frac{c}{64} (4 ρ^{*} - n_{1 j i} n_{2 j i}) - \frac{(1 - μ) α^{2} β^{2}}{4} ρ^{*}

+ \frac{α^{4}}{8} n_{1 j i} (b_{j i}^{*} β + m_{2 j i}) + \frac{β^{4}}{8} n_{2 j i} (a_{j i}^{*} α + m_{1 j i} + \frac{μ α^{2} β^{2}}{8} m^{*}]\}

\times \{9 (S - S_{1} + \sum_{i = 1}^{k} \sum_{j = 1}^{r} \frac{1}{α β} [- 2 (3 ρ + 2 m_{1 j i} m_{2 j i}) + \frac{1}{16} (12 ρ^{*} - n_{1 j i} n_{2 j i}) + \frac{1}{2} m *]\}

{\times \{9 (S - S_{1} + \sum_{i = 1}^{k} \sum_{j = 1}^{r} \frac{1}{α β} [- 2 (3 ρ + 2 m_{1 j i} m_{2 j i}) + \frac{1}{16} (12 ρ^{*} - n_{1 j i} n_{2 j i}) + \frac{1}{2} m *]\}}^{- 1},

where $a$ , $b$ – the length and width of the sheet respectively.

Several notations are introduced here as follows:

6

c = {(α^{2} + β^{2})}^{2}, S = a b, S_{1} = \sum_{i = 1}^{k} \sum_{j = 1}^{r} a_{j i}^{*} b_{j i}^{*}, S_{1} = \sum_{i = 1}^{k} \sum_{j = 1}^{r} a_{j i}^{*} b_{j i}^{*},

a_{j i}^{*} = x_{2 j i} - x_{1 j i}, b_{j i}^{*} = y_{2 j i} - y_{1 j i}, m_{1 j i} = s i n 2 α x_{1 j i} - s i n 2 α x_{2 j i},

m_{2 j i} = s i n 2 β y_{1 j i} - s i n 2 β y_{2 j i}, ρ = m_{1 j i} b_{j i}^{*} β + m_{2 j i} a_{j i}^{*} α, c_{1}^{*} = \frac{3}{4} c - α^{2} β^{2},

n_{1 j i} = s i n 4 α x_{1 j i} - s i n 4 α x_{2 j i}, n_{2 j i} = s i n 4 β y_{1 j i} - s i n 4 β y_{2 j i},

\bar{ρ} = m_{2 j i} a_{j i}^{*} α - m_{1 j i} b_{j i}^{*} β, ρ^{*} = n_{2 j i} a_{j i}^{*} α + n_{1 j i} b_{j i}^{*} β, m^{*} = m_{1 j i} n_{2 j i}^{} + m_{2 j i} n_{1 j i}^{} .

These formulae are used to calculate the natural frequencies of the rectangular plate with any number of holes and with fixed edges. We can see that even for the rectangular plates, equations appear to be difficult. Solving them is possible only by numerical procedures. We can’t apply an analytical solution of the equations regarding plates and the freeform holes. It would be appropriate to use here the finite-element model to calculate the natural frequencies of these details [7-10].

3. Finite-element model

At the first stage of research, the calculation had been made for natural frequencies of the rectangular perforated grill of the terminal case, the finite-element model had been applied, and then we compared collected data with the results of the analytical calculations and the full-scale experiment. The full-scale experiment had been conducted with the help of the frequency meter and the accelerometer sensor.

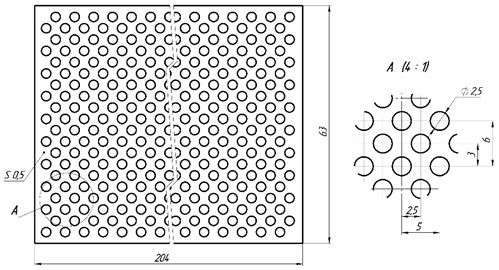
Fig. 3 shows a schematic of a carbon plate grill used to cool the terminal device.

Fig. 3Vent grill schematic

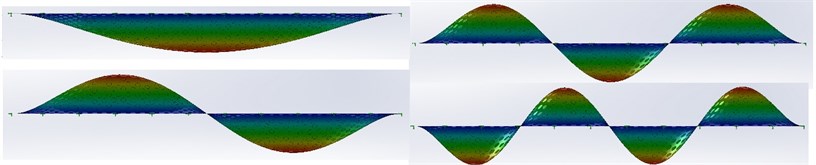
The finite-element grid is built based on the triangular shell finite elements. At the edges of the grill the movement and nodal point rotation restrictions are installed. Fig. 4 illustrates the first four modes of oscillation.

Fig. 4Natural modes of grill oscillation

Sheet 1 shows the comparison of natural frequency values corresponding to vibration mode data, which was collected during the experiment, analytically and by implementing the finite-element model.

Table 1Difference between the results received by the finite element model and by the experiment

No harmonic	Experiment, Hz	Analytical calculation, Hz	Finite element model, Hz
1	654	648	656
2	710	700	714
3	820	810	821
4	1205	1995	1209

Table 1 shows that the difference between the results received by the finite element model and by the experiment doesn't exceed 0,5 %; that fact proves the correctness of the finite-element model. The first natural frequency gets into the vocal range. In practice, that manifests as an appearance of side tones while reproducing high pitched woman voices. To increase the grill thickness is the easiest way to increase the natural frequency. The finite-element model was implemented for grills of different thicknesses (0,5; 0,8; 1; 1,5 mm). Results can be found in Table 2.

Table 2Results of finite-element model

Grill, mm	The first natural frequency, Hz
0,5	656
0,8	1050
1	1312
1,5	1968

With a grill thickness of 0.8 mm and more, the first natural frequency exceeds 1000 Hz. Tests of the terminal device with the 0.8 mm grill thickness confirmed, that specific sidetone previously present at the frequency of 700 Hz disappeared.

During the second stage of the research, the analysis had been done of the influence of the grill perforation parameters on the value of the natural frequency. An increase in the total area of the holes in the grill leads to the enhancement of the terminal case heatsink and as a consequence to processor temperature decrease. That’s why the increase of that parameter is so important in practice. The calculations were performed at the same grill thickness of 0.8 mm and with different parameters of perforation (Table 3).

Table 3The influence of the grill perforation parameters

Parameters of perforation	Total perforation area, mm²	The first natural frequency, Hz
Round hole Ø 2, pitch 2,5	3927	1050
Round hole Ø 3, pitch 5	5872	1026
Round hole Ø 5, pitch 8	5400	1026
Square hole 5×5, pitch 8	5000	934
Square hole 6×6, pitch 9	6300	870

Comparison of results of the grill frequency simulation with the different parameters of perforation shows that if we maintain the constant perforation pitch, the value of the first natural frequency is directly linked to the value of the total perforation area and almost doesn’t depend on the shape of the holes. The above mentioned result suggests, that when we choose the type of perforation, we must take two things into consideration. The total hole area, to make cooling effective, and the requirements to the industrial design of grill’s outlook. The shape of the holes has almost no impact on the frequency parameters of the grills.

4. Conclusions

Obtained models made it possible to increase vibration stability of terminal device cases with passive cooling, which are used in the voice communication control systems by air traffic controllers. Research data has been produced during calculations and finite-element simulation, values of natural frequencies of the cooling grills of terminal devices were retrieved. Based on the results of calculations several changes were implemented into the terminal case grill design, which made it possible to increase the quality of audio reproduction of voice information saving the heatsink rate of the processor at the same time.

References

Levin E. and Zaynal S., “Voice communication system for air traffic control. Development and evaluation of a prototype,” Master of Science Thesis in Software Engineering and Technology, Chalmers University of Technology University of Gothenburg Department of Computer Science and Engineering, Göteborg, Sweden, 2011.

Search CrossRef
R. Cox, S. de Campos Neto, C. Lamblin, and M. Sherif, “ITU-T coders for wideband, superwideband, and fullband speech communication,” IEEE Communications Magazine, Vol. 47, No. 10, pp. 106–109, Oct. 2009, https://doi.org/10.1109/mcom.2009.5273816

Publisher
Preobragenskiy I. N., Stability and Oscilations of Plates and Shells with the Holes. Moscow: Mashinostroenie, 1981.

Search CrossRef
L. V. Kurpa, “Natural vibrations of plates with holes,” Soviet Applied Mechanics, Vol. 15, No. 2, pp. 173–175, Feb. 1979, https://doi.org/10.1007/bf00884587

Publisher
R. F. Hegarty and T. Ariman, “Elasto-dynamic analysis of rectangular plates with circular holes,” International Journal of Solids and Structures, Vol. 11, No. 7-8, pp. 895–906, Jul. 1975, https://doi.org/10.1016/0020-7683(75)90012-8

Publisher
Nemirovskiy B. Y. and Preobragenskiy I. N., Dynamic Tasks of the Theory of Plates and Shells with the Holes. Moscow: Nauka, 1973.

Search CrossRef
H. Hakula and M. Laaksonen, “Frequency response analysis of perforated shells with uncertain materials and damage,” Applied Sciences, Vol. 9, No. 24, p. 5299, Dec. 2019, https://doi.org/10.3390/app9245299

Publisher
E. Frulloni, J. M. Kenny, P. Conti, and L. Torre, “Experimental study and finite element analysis of the elastic instability of composite lattice structures for aeronautic applications,” Composite Structures, Vol. 78, No. 4, pp. 519–528, Jun. 2007, https://doi.org/10.1016/j.compstruct.2005.11.013

Publisher
D. Chapelle and K. J. Bathe, The Finite Element Analysis of Shells. Berlin/Heidelberg, Germany: Springer, 2003.

Publisher
M. J. Jhung and S. O. Yu, “Study on modal characteristics of perforated shell using effective Young’s modulus,” Nuclear Engineering and Design, Vol. 241, No. 6, pp. 2026–2033, Jun. 2011, https://doi.org/10.1016/j.nucengdes.2011.02.00

Publisher

About this article

Received

08 November 2021

Accepted

23 November 2021

Published

02 December 2021

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2021.22285

Keywords

natural oscillation frequency

voice communication control system (VCCS)

telecommunication terminals

grill oscillation

finite-element model

perforated shell

cooling

heatsink

Acknowledgements

This work was done with the support of Russian Science Foundation, Project No. 19-19-00065.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 01 21

Research on estimation and control methods of natural frequency of irregular building structure vibration

Guicai Song

Research article

2019 11 28

Free vibration analysis of simply supported rectangular plates

Ganesh Naik Guguloth, Baij Nath Singh, Vinayak Ranjan

Research article

2019 09 30

Effects of mechanical non-linearity on the dynamic behaviour of ring-based inertial rate sensors

Violetta Di Napoli, Stewart McWilliam, Atanas A. Popov

Research article

2019 03 31

Self-synchronization features of inertial vibration exciters in two-mass system

Grigory Panovko, Alexander Shokhin

G. Korendyasev and M. Asaturov, “Research on the oscillation of cooling grills used for terminal devices for voice communication control systems used by air traffic controllers,” Vibroengineering PROCEDIA, Vol. 39, pp. 11–16, Dec. 2021, https://doi.org/10.21595/vp.2021.22285

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2021.22285
UR  - https://doi.org/10.21595/vp.2021.22285
TI  - Research on the oscillation of cooling grills used for terminal devices for voice communication control systems used by air traffic controllers
T2  - Vibroengineering PROCEDIA
AU  - Korendyasev, George
AU  - Asaturov, Mikhail
PY  - 2021
DA  - 2021/12/02
PB  - JVE International Ltd.
SP  - 11-16
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Korendyasev_2021,
	doi = {10.21595/vp.2021.22285},
	url = {https://doi.org/10.21595/vp.2021.22285},
	year = 2021,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	pages = {11--16},
	author = {George Korendyasev and Mikhail Asaturov},
	title = {Research on the oscillation of cooling grills used for terminal devices for voice communication control systems used by air traffic controllers},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]G. Korendyasev and M. Asaturov, “Research on the oscillation of cooling grills used for terminal devices for voice communication control systems used by air traffic controllers,” Vibroengineering PROCEDIA, pp. 11–16, Dec. 2021, doi: 10.21595/vp.2021.22285.

Copy IEEE

Copied to clipboard!

Korendyasev, George, and Mikhail Asaturov. “Research on the Oscillation of Cooling Grills Used for Terminal Devices for Voice Communication Control Systems Used by Air Traffic Controllers.” Vibroengineering PROCEDIA, December 2, 2021, 11–16. https://doi.org/10.21595/vp.2021.22285.

Copy Chicago

Copied to clipboard!

Research on the oscillation of cooling grills used for terminal devices for voice communication control systems used by air traffic controllers

Abstract

1. Introduction

2. Mathematical model of oscillation

3. Finite-element model

4. Conclusions

References

About this article

Related Articles