Bearing fault diagnosis based on adaptive mutiscale fuzzy entropy and support vector machine

2.1. HLMD method and calculation procedures

In LMD method, a multi-component signal can be decomposed into a sum of PF components, each of which is the product of an envelope signal and a pure FM signal. Compared with EMD method, the prominent advantage of LMD is that it directly gives access to the calculations of the IA and IF of each PF, avoiding performing the Hilbert transform (HT). However, the original LMD method employs the moving algorithm (MA) approach to compute the local mean function $m\left(t\right)$ and envelope estimation function $a\left(t\right)$, which can be easily affected by noise of the inspected signals and produce errors in the smoothing process [13]. Also the sliding step sizes selection is an unsolved problem in the MA algorithm.

To overcome the drawbacks of original LMD, Deng L. introduced the cubic spline interpolation approach to construct the local mean function $m\left(t\right)\mathrm{}$and envelope estimation function $a\left(t\right)$ [16]. However, the envelopes constructed by cubic spline interpolation may produce outstanding over and undershoot problems [17]. In this paper, the cubic Hermite interpolation approach is introduced to obtain local mean$\mathrm{}$and envelope estimation functions.

The definition of the cubic Hermite interpolation is given as follows.

Given a series of discrete date $a=x_0<x_1<\cdots x_n=b$ and $(x_i,y_i,d_i)$, the $y_i$ is the value at time $x_i$ ($i=$ 0, 1, 2,…, $n$), $d_i$ is the first derivative at each time $x_i$, $h_i=x_{i+1}-x_i$, $t=x-x_i/h_i$ and ${\lambda }_i$ is any real numbers. Then in each ${[x}_i,x_{i+1}]$ can be written as:

where ${\alpha }_i\left(t\right)$, ${\alpha }_{i+1}\left(t\right)$, ${\beta }_i\left(t\right)$ and ${\beta }_{i+1}\left(t\right)$ are basis functions of the cubic Hermite interpolation, which can be expressed as:

Based on the computation of local mean function $m\left(t\right)$ and envelope estimation function $a\left(t\right)$ using cubic Hermite interpolation. For a given signal $x\left(t\right)$, the calculation steps of HLMD method can be summarized as follows:

Step 1: Identify all local extrema $n_i$ of the original signal $x\left(t\right)$, and the mirror-symmetric extension method is used to extend endpoints to obtain a new extreme point sequence $X_k$.

Step 2: Calculate the upper envelop $E_{max}\left(t\right)$ and lower envelop $E_{min}\left(t\right)$ of the signal being analyzed by using cubic Hermite interpolation algorithms.

Step 3: Compute local mean function $m_{11}\left(t\right)$ and envelope estimation function $a_{11}\left(t\right)$ using the upper and lower envelopes according to Eq. (3) and Eq. (4):

Step 4: The local mean function $m_{11}\left(t\right)$ is subtracted from the original data $x\left(t\right)$:

where $h_{11}\left(t\right)$ is then amplitude demodulated by been divided by$a_{11}\left(t\right)$:

The envelope $a_{12}\left(t\right)$ of $s_{11}\left(t\right)$ can then be calculated by step (1) and (2). If the envelope function $a_{12}\left(t\right)=\mathrm{}$1, stop the procedure and take $s_{12}\left(t\right)$ as the first purely frequency modulated signal. If the envelope function $a_{12}\left(t\right)\ne \mathrm{}$1, regard $s_{11}\left(t\right)$ as the original singal and repeate the steps (1)-(4) continues $n$ times until a purely frequency modulated signal $s_{1n}\left(t\right)$ is obtained:

in which:

The objective of the itearation is to obtain a signal whose envelope function should satisfy $a_{1n}\left(t\right)=\mathrm{}$1.

Step 5: The corresponding envelope is obtained by Eq. (9):

The envelope function $a_1\left(t\right)$ is then multipied by the purely frequency modulated signal $s_{1n}\left(t\right)$ and then the first product function $P{F}_1\left(t\right)$ can be written as:

In fact, the instantaneous amplitude of $P{F}_1$ is $a_1\left(t\right)$ and the instantaneous frequency of $P{F}_1$ can be calculated by the pure frequency modulated signal $s_{1n}\left(t\right)$ according to Eq. (11):

Step 6: This derived $P{F}_1\left(t\right)$ is then subtracted from the original time series $x\left(t\right)$, resulting in a new function $u_1\left(t\right)$, which represents a smoothed version of the original data since the highest frequency oscillations have been removed from it. Regard $u_1\left(t\right)$ as a new data and repeat the above procedure $k$ times until $u_k\left(t\right)$ is a constant or contains no more oscillations:

Thus, the original signal can be reconstructed $k$ product functions and a residual $u_k\left(t\right)$ according to:

where $u_k\left(t\right)$ is the residue and $k$ is the number of PF components .

It should be noted that $a_{ij}\left(t\right)$ is envelope estimation function, $i$ and $j$ denotes the $i$th component in the $j$th iterations. In practice, a variation $\delta$ can be determined in advance. If ${1-\delta \le a}_{1(n+1)}\left(t\right)\le 1+\delta$, then iterative process would be stopped. Also, the decomposition stops when the $u_i\left(t\right)$ becomes monotonic function, usually, the monotonic criterion is determined by the number of the extrema of $u_i\left(t\right)$. If the number of the extrema of $u_i\left(t\right)$ is no more than 3, then the $u_i\left(t\right)$ is monotonic and the decomposition is completed.

2.2. Application to simulation signals

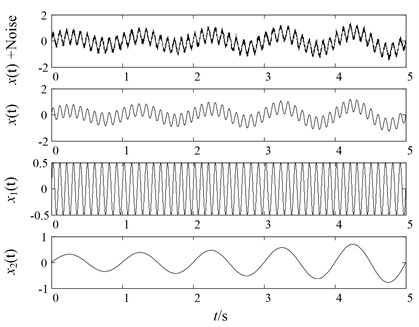
In order to validate the effectiveness of the proposed HLMD method, a simulation signal $x\left(t\right)$ is employed to conduct the comparisons among original LMD, HLMD and SLMD. The simulation signal consists of an AM-FM signal $x_1\left(t\right)$, an AM signal $x_2\left(t\right)$ and a white noise, set sampling frequency 1000 Hz, the sampling time is 5 seconds:

The waveforms of simulation signals are shown in Fig. 1.

Fig. 1Simulation signal and its three components

To begin with, original LMD, HLMD and SLMD methods are all applied to decompose the noisy signal in Eq. (14). The decomposition results of the three methods are represented in Fig. 2, Fig. 3 and Fig. 4, respectively. It should be noted that the boundary conditions of the simulation signal have been handled by the mirror-symmetric extension [18] and the iteration stop condition is ${1-\delta \le a}_{ij}\left(t\right)\le 1+\delta$, where $\delta =\mathrm{}$10^-4.

Fig. 2Original LMD decomposition results of noisy signal

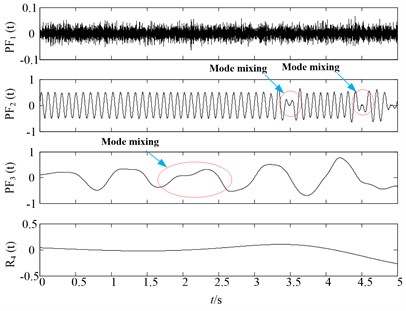
Fig. 3HLMD decomposition results of noisy signal

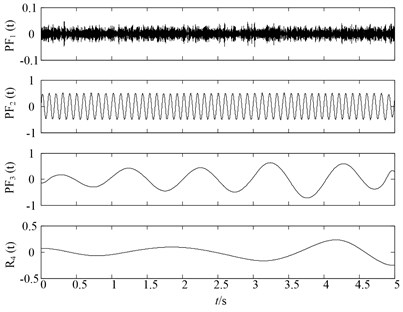
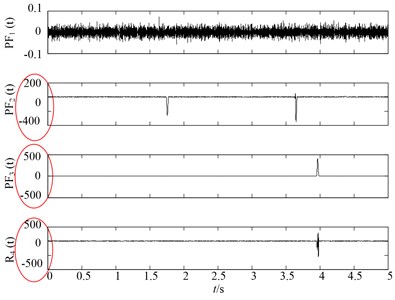
It can be observed from Fig. 2 that the first PF component of original LMD method is the noisy signal and second and third $PF$ are corresponding to the $x_1\left(t\right)$, $x_2\left(t\right)$ of the simulation signal. However, it can be easily found that the slight distortion phenomena occur in the second and third $PF$ components of original LMD. While in the Fig. 3, there are no such distortion phenomenon in the $P{F}_2\left(t\right)$ and $P{F}_3\left(t\right)$ of HLMD, resulting in more accurate decomposition results. For comparison purpose, the SLMD is also employed to decompose the noisy signal. Fig. 4 shows the decomposition results of SLMD method, from which we can find that SLMD decomposition results are serious distorted, losing the physical meaning.

Fig. 4SLMD decomposition results of noisy signal

Secondly, to further compare the decomposition ability of original LMD, HLMD and SLMD methods, the demodulation technique is utilized to calculate instantaneous frequency (IF) and instantaneous amplitudes (IA) and the time-frequency representation (TFR) of the PFs obtained by the three methods are shown in Fig. 5. From Fig. 5(a) (the TFR of PFs obtained by the original LMD method), it is clear that the distortion appears in the second and third PF of original EMD (with IF 10 Hz and 2 Hz, respectively), which is due to the errors in the smoothing process using the MA. Conversely, the TFR of PFs derived from HLMD can ameliorate the fluctuation phenomenon with less distortion. Furthermore, the first horizontal line in Fig. 5(b) (with IF 10 Hz) has a narrower bandwidth than that of original LMD method. Additionally, it can be easily observed that the TFR of PFs derived from SLMD in Fig. 5(c) are totally anamorphic. Therefore, the above analysis results verify that HLMD can significantly restrict the mode mixing phenomena and get more accurate IF and IA compared with other two methods.

Fig. 5The time-frequency distribution of the PFs derived from the three LMD methods: a) the time-frequency distribution of original LMF method, b) the time-frequency distribution of HLMD method and c) the time-frequency distribution of SLMD method

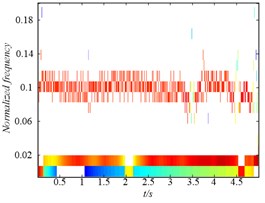
a)

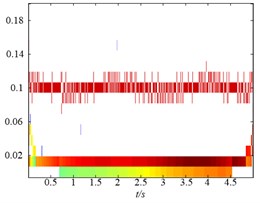
b)

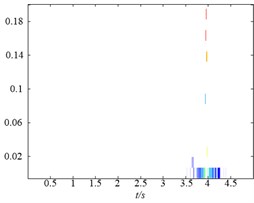
c)

Lastly, three assessing indexes are chosen to assess the decomposition performance. Orthogonal index ($OI$), root mean squared error (RMSE) and calculation efficiency are considered as assessing indicators. Firstly, the definitions of the three assessing indicators are describes as follows. The $OI$ is defined as [19]:

where $N_{PF}$ is the number of PFs. $N$ is the length of the $PF$. ${PF}_{ik}\left(t\right)$ and ${PF}_{jk}\left(t\right)$ are the $i$th and $j$th PF at sifting step $k$, respectively. $x_k$ is the original signal and $r_k$ is the residual after LMD decomposition. Theoretically, the PFs and the final residual obtained by LMD decomposition are expected to be mutually orthogonal, which means the $OI$ index is proposed to be zero. Therefore, the smaller $OI$ (more close to zero) means the better decomposition results. Secondly, the RMSE definition is as follows:

where $s\left(t\right)$ and $PF\left(t\right)$ are the original defined component and the corresponding decomposed component, respectively. RMSE is utilized to assess the decomposition accuracy. In theory, the RMSE value should be zero, hence, the smaller RMSE value indicates that the obtained mono-components are more precise and more close to real $x_1\left(t\right)$ and $x_2\left(t\right)$ in Eq. (14). Eventually, we need to discuss the calculation efficiency of the three methods. The computer with 3.3 GHz i3-Core CPU, 4.0 GB RAM and MATLAB (R2010b) platform are employed to conduct the simulation.

Since the decomposition results of SLMD are serious distortion, it has been omitted in the following comparisons. We only conduct the comparisons between original LMD and HLMD methods, the compassion results are shown in Table 1.

We can draw the following conclusions from Table 1. Firstly, it can be found that the RMSE values of $P{F}_2\left(t\right)$, $P{F}_3\left(t\right)$ (corresponding to the $x_1\left(t\right)$ and $x_2\left(t\right)$ of original signal) derived from HLMD method (0.0578, 0.0756) are smaller than that of original LMD method (0.1852, 0.2393), it indicate that the decomposition results of HLMD are more close to the real mono-component of the original signal $x_1\left(t\right)$ and $x_2\left(t\right)$, respectively. Secondly, the consuming time of original LMD is 125.72 s, which is much more than that of HLMD method. Lastly, compared with original LMD method, HLMD has a smaller $OI$ value, which shows that HLMD method is super to original HLMD method in the orthogonality.

The comparative results illustrate that HLMD consumes less computation time and generates more accurate decomposition results than original LMD. The above analysis results can be explained in the following way.

Since the cubic Hermite approach is first-order smoothness, it not only has enough flexibility to fit the local extreme points of the signal but also has an excellent conformal characteristic, which is more suitable for fitting envelope of the rolling bearing vibration signal than the cubic Hermite approach.

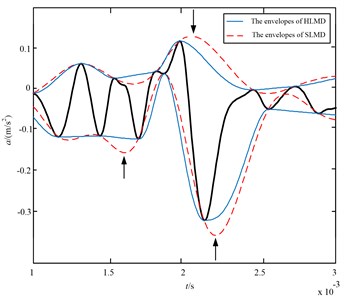
Furthermore, a section of data intercepted from the simulation signal in the sifting process is taken to find out the cause for the above comparison results, which is shown in Fig. 6. It is easy to find that envelope-lines fitted by the cubic spline interpolation in red dashed line have serious over and undershoot problems, which are denoted by arrows in Fig. 6. Whereas, the envelope-lines fitted by Hermite interpolation in blue line can eliminate the over and undershoot problems of cubic spline interpolation obviously. Hence, the HLMD can obtain more reliable envelope-lines and accurate decomposition results.

To summarise, the original LMD method uses MA to calculate the local mean function $m\left(t\right)$ and envelope estimate function $a\left(t\right)$, which can be easily affected by noise of the inspected signals and generate errors in the smoothing process [13, 14]. Whereas, HLMD adopts the cubic Hermite interpolation method instead of MA to construct the local mean function $m\left(t\right)$ and envelope estimate function $a\left(t\right)$. The cubic Hermite interpolation has a continuous first derivative property at the node and the obtained lines have an excellent conformal characteristic, which can decrease smoothing errors of MA effectively. Therefore, in this paper HLMD method is taken to preprocess the vibration signals, resulting in a series of scale-dependent PFs.

Fig. 6The envelopes of the Hermite interpolation (blue line) and optimized rational spline (red dashed line) interpolation

3.1. The basis of multi-scale fuzzy entropy (MFE) and the disadvantages

The definition and calculation procedures of sample entropy (SE) are described by [20]. Since the similarity definition of the two vectors is mainly according to the Heaviside function, which is jumping and not according with the boundaries of the actual times series, whereby the two classes are mostly ambiguous. To overcome the disadvantages of SE, fuzzy entropy (FE) is developed, which used the Gaussian function to replace the Heaviside function. The detailed steps of FuzzyEn are given in literature [6]. Recently, the multi-scale analysis algorithm was developed by Costa [7] to quantify the complexity of time series in different scales. Based on the concept of multi-scale analysis, MFE method was proposed by Zheng et al. [9], which can measure the complexity of time series over the different scales.

MFE algorithm contains two steps. Firstly, apply the coarse-grained procedure to get multiple scale time series from the original time series. Then, calculate the FuzzyEn at each coarse-grained time series. Two procedures of MFE algorithm are briefly described as follows.

1) To obtain the coarse-grained time series at a scale factor of $\tau$, the original time series is divided into disjointed windows of length τ, and the data points are averaged inside each window. Namely, the coarse-grained time series at a scale factor of $\tau$ ($\tau$ is a positive integer), ${\mathbf{y}}_j^{\tau }$ can be constructed according to Eq. (17):

2) In MFE analysis, the FuzzyEn of each coarse-grained time series is calculated based on FuzzyEn calculation steps and then plotted as the function of the scale factor $\tau$, which can be expressed as:

Note that the $r$ in the calculation for different scales is same, which is obtained by the $r=\lambda SD$. $SD$ is the standard deviation of the original time series.

However, in the MFE method, the scales are determined by the “coarse-grained” procedure. From Eq. (17), it can be found that the length of the coarse grained time series is equal to the length of original time series divided by the scale factor $\tau$. Namely, the coarse-grained procedure of MFE is essentially a linear smoothing and decimation of the original time series, eliminating high-frequency components. Due to the linear operations of coarse-grained procedure, it is unsuitable to extract the fault feature using MFE in the different scales when analyzing the nonlinear and non-stationary signals.

3.2. AMFE algorithm

To overcome the disadvantages of MFE, a novel fault feature extractor called adaptive multiscale entropy (AME) is proposed in this paper. AMFE can estimate the entropy of the signal over multiple adaptive scales that are intrinsically determined using HLMD method. The AMFE is mainly composed of three procedures: (1) Perform HLMD method to decompose the rolling bearing data into a sum of PFs under different scales; (2) Generate the adaptive scales by consecutively removing the PF component with high frequency; (3) Calculate the FuzzyEn of the obtained adaptive scales. Namely, the consecutively removing PF component procedures essentially represent the mutiscale low-pass filtering of the original signal. The main steps of AMFE are described as follows.

Algorithm: Adaptive mutiscale fuzzy entropy (AMFE):

1) The measured rolling bearing vibration signals are firstly decomposed by HLMD to acquire a set of $PF$ components in different scales and the residual is considered as the last $PF$ component, denoted as ${PF}_1\left(t\right)$, ${PF}_2\left(t\right)$,…, ${PF}_N\left(t\right)$:

2) Generate the adaptive scales $S_f^k\left(t\right)$ by consecutively removing the $PF$ component with high frequency from the original signal via Eq. (20):

where $N$ denotes the number of the $PF$ components.

3) Calcluate the FuzzyEn value of the obtaied adaptive scales $S_f^k\left(t\right)$ to fulfill the AMFE values:

here set the $r=$ 0.15$SD$, $m=$ 2 and $n=$ 2.

From the above steps of AMFE, we can find that the procedures of obtaining different scales in AMFE are really like the “coarse-grained” procedure. However, the scales in AMFE are obtained using HLMD, which are adaptive to the time series. Meanwhile, since the HLMD is complete data-driven time-frequency technique, the fault information stored in different frequency components are preserved, allowing an efficient search of discriminating features.

3.3. Comparison between AMFE and MFE

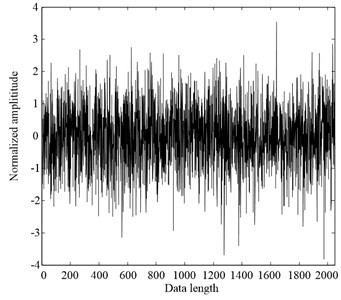
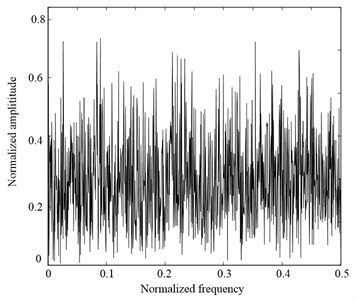
In order to investigate the estimate performance of AMFE method, a white noise simulation signal is utilized to conduct the comparisons between AMFE and MFE methods. The waveforms of the white noise and its Fourier transform spectrum are illustrated in Fig. 7. As can be seen from its spectrum, the complexity of white noise is uniform distribution.

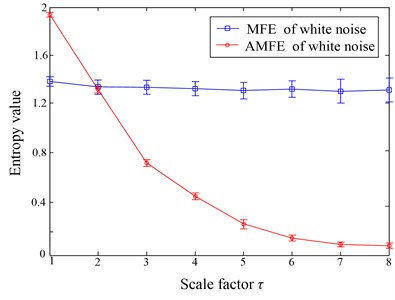
AMFE and MFE methods are both used to analyze 100 independent white noises, each of which contains 1000 data points. The error bar calculated from 100 independent noise signals at each scale are shown in Fig. 8. The following conclusions can be drawn from Fig. 8. Firstly, the FuzzyEn curve of white noise obtained by AMFE method decreases monotonically with scale increasing, which is consistent with the conclusions drawn in literature [21]. In contrast, the FuzzyEn curve obtained by traditional MFE method is nearly independent of scale, which can’t reflex the dynamic change of time series. It is well known that the error bar at each scale indicates the standard deviation (SD) of a FuzzyEn value. As seen the error bar of white noise in Fig. 8, the SD of AMFE is less than that of MFE, which indicate that AMFE has a more stable performance in estimating the complexity of the time series.

Fig. 7The waveform and FT spectrum of white noise

a)

b)

Fig. 8AMFE and MFE analysis of white noise

4.1. The fault feature extraction based on AMFE and SVM

Based on the superiorities of AMFE and SVM, a novel rolling bearing fault diagnosis approach is presented in this paper, it can be summarized as follows:

1) When the machine operates under different working conditions, the vibration signals are measured by acceleration sensors at a sampling frequency $f_s$. The sensor-based vibration signals are preprocessed by the HLMD method and a series of PF components are obtained. Remove consecutively the PF component with high frequency from the original signal to acquire the adaptive scales $S_f^k\left(t\right)$, denoted as fine-course procedure;

2) FuzzyEn algorithm is employed to calculate the obtained adaptive scales $S_f^k$(t). In the whole paper, we define the number of adaptive scales $k$ from 1 to 6 ($k=$ 1 to 6) and the FuzzyEn values of each coarse grained time series obtained by Eq. (20) is computed with the dimension $m=$ 2 and tolerance $r=$ 0.15$SD$.

3) The obtained fault features are fed into fault classifier SVM to identify the different health conditions.

4.2. Experimental validation

In this section, an actual rolling bearing data is utilized to examine the utility of proposed algorithm. The test bearing data was obtained from the Bearing Data Center of Case Western Reserve University Bearing Data Center [22]. Fig. 9 gives the platform of the experiment system. The 6205-2RS JEM SKF deep groove ball bearing is used in this test. The vibration signals of bearing were collected under four conditions including normal condition, the ball fault condition, the outer race fault condition and the inner race fault condition. In each bearing fault condition, the bearing was seeded with signal point using the electro-discharge machining with fault diameters of 0.1778 mm, 0.3556 mm, 0.5334 mm and 0.7112 mm. An accelerometer was mounted on the front section end to collect the vibration signal. In addition, the sampling frequency is 12000 Hz and the shaft rotating speed of the motor is 1797 rpm without motor load.

Fig. 9The platform of rolling bearing experiment system

To demonstrate the effectiveness of the methodology can be applied to recognize the different categories and severities of rolling bearings. The experimental vibration signals are composed of four fault categories and each fault category contains different levels of severity. Based on the different fault categories and various fault degrees, actually, the experimental analysis is an seven-class recognition problem. The vibration signals in the experiment are divided into several non-overlapping segments with the length of 2,000. There are 40 samples for each bearing condition, and there are total 280 samples, in which 140 samples will be randomly selected as the training data, and the residual 140 samples will be testing data. The detailed numbers of samples description for each bearing condition are shown in Table 2.

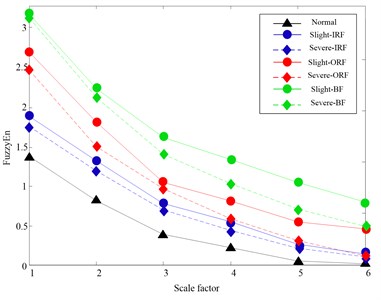
Fig. 10 gives the time domain waveforms of vibration signals under four fault categories case, respectively. According to procedures in Section 4.1, HLMD method is firstly adopted to decompose the vibration signal into a sum of mono-components, the decomposition results of bearing at normal condition is shown in Figs. 11 (other bearing working conditions are omitted for saving space). Subsequently, the AMFE is completed by calculating the FuzzyEn of residual sums of the PFs though consecutively removing the PF component with high frequency from the original signal. The obtained results of AMFE is shown in Fig. 12, from which it can be observe that the FuzzyEn exhibits the decreased trend as the fine PFs with high frequency are consecutively removed. Moreover, the four health conditions can be significantly distinguished using AMFE method.

Fig. 10The vibration signals of each rolling bearing condition

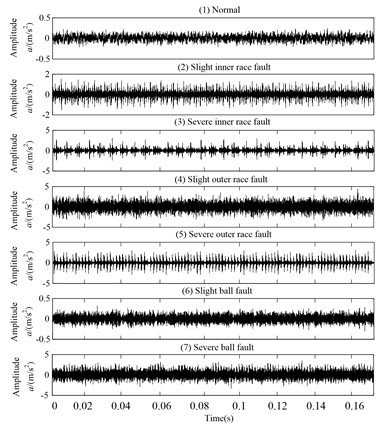
Fig. 11HLMD decomposition results of bearing with normal condition

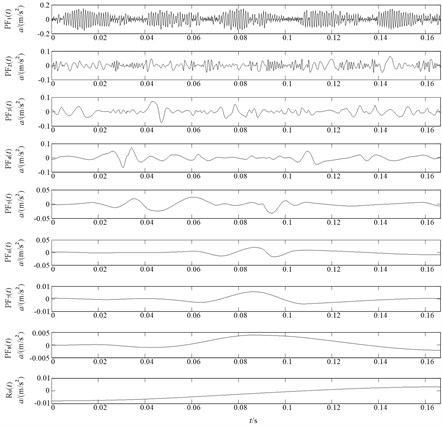
Fig. 12AMFE over 6 scales of the original vibration signal

Naturally, according to the flowchart of AMFE and SVM algorithm, the obtained fault features are fed into fault classifier SVM to identify the different health conditions. As mentioned above, 140 groups of data are selected randomly as training set to train the SVM-classifier and the remaining 140 group of data are taken as testing set to test the trained SVM-classifier. In addition, PSO algorithm is applied to calculate the optimal penalty parameter $C$ and kernel parameter $\gamma$ according to the training data [23]. Hence the testing set are fed into the trained model to achieve the fault identification, and the output testing results are shown in Table 3. It can be found no samples of the four fault types are misclassified, and the training and testing accuracy are both 100 %, which demonstrate the proposed AMFE and SVM method is feasible and effective in the rolling bearing fault diagnosis.

For comparison purpose, the MFE method is also used to analyze the rolling bearing data, and the fault features obtained by MFE are also fed into SVM for pattern identification. Through the same process in AMFE-SVM method, which includs the number of training and testing samples and the parameter selection of SVM, the classification results based on MFE and SVM are shown in Table 4. It can be easily found that there are one sample with slight and severe inner race fault, severe ball fault as well as three samples with slight ball fault are misclassified, which coincide well with the above analysis. The total testing classification accuracy of 96.4 %, while the corresponding testing classification accuracy of AMFE is 100 %. The comparisons demonstrate that the proposed method can present better distinguishability and superior performance in identifying various fault patterns of rolling bearing.