Measurement of stability of a pipe system with flowing fluid

2.1. Model for the analysis of stability of a pipe system with flowing fluid

$x$, $y$ and $z$ denote the axes of the system of coordinates. The finite element of a two dimensional beam representing the pipe in the plane $xOz$ has three nodal degrees of freedom: the displacement in the direction of the $x$ axis denoted as $u$, the displacement in the direction of the $z$ axis denoted as $w$ and the rotation about the $y$ axis denoted as ${\theta }_y$.

The displacements in the direction of the longitudinal axis of the pipe $s$ and in the direction of the axis perpendicular to $s$ and located in the plane $xOz$ are denoted as $\stackrel{-}{u}$ and $\stackrel{-}{w}$ and they are related with $u$, $w$ as:

where $\xi$ is the local coordinate of the finite element of the pipe and $ds/d\xi =\sqrt{{\left(dx/d\xi \right)}^2+{\left(dz/d\xi \right)}^2}.$

The following notation is used:

where $N_i$ are the shape functions of the one dimensional finite element of the pipe.

Also it is assumed:

The stiffness matrix of the pipe has the usual form:

where $E$ is the modulus of elasticity of the pipe, $\nu$ is the Poisson’s ratio of the pipe, $r$ is the internal radius of the pipe, $R$ is the external radius of the pipe and $\left[B\right]=\left[\left[{\stackrel{-}{N}}_2^{\text{'}}\right]+\left[{\stackrel{-}{N}}_3\right]\right].$

The supplementary stiffness matrix of the model of a pipe because of the motion of the fluid in it has the form:

where ${\rho }_f$ is the density of the fluid filling the pipe and v is the velocity of the fluid inside the pipe.

The total stiffness of the pipe is equal to $\left[K\right]-\left[K_v\right]$. If the velocity is changed $\sqrt{\lambda }$ times, then the stiffness becomes $\left[K\right]-\lambda \left[K_v\right]$. This results in the eigenproblem for the determination of critical velocities and stability eigenmodes.

2.2. Analysis and measurement of stability of a pipe system with flowing fluid

The structure consists from a lower straight pipe and an upper straight pipe both of them having fixed ends (all of the generalized displacements equal to zero) and they are assumed filled with water. The midpoints of both pipes are connected by an empty pipe perpendicular to them. Length of the structure is 2 m and the distance between the lower and upper pipes is 0.4 m.

The following parameters are assumed: modulus of elasticity of the pipes $E=$ 6·10⁸ Pa, Poisson’s ratio of the pipes $\nu =$ 0.3, density of the fluid filling the two pipes ${\rho }_f=$ 998 kg/m³, velocity of the fluid in the lower pipe is assumed to be equal to $v=$ 1 m/s, velocity of the fluid in the upper pipe is assumed to be equal to $v=$ –1 m/s, internal radius of the pipes $r=$ 0.004 m, external radius of the pipes $R=$ 0.006 m.

The first stability eigenmodes are presented in Fig. 1. The fourth and the fifth eigenmodes correspond to the same eigenvalue.

In order to perform precise measurements of stability of a pipe system the measurements of deflections of the pipes are to be performed not at the nodes of the stability eigenmodes and preferably at the places with maximum deflections. In practical applications usually the first eigenmode is important. Thus from the presented images of deflections the locations of measurement devices may be chosen.

Fig. 1The first stability eigenmodes of the pipe system: a) the first eigenmode, b) the second eigenmode, …, j) the tenth eigenmode

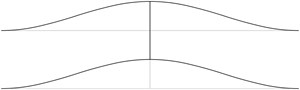
a)

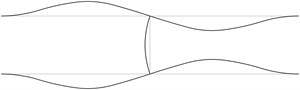
b)

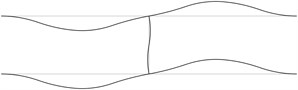
c)

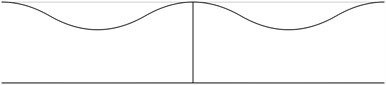
d)

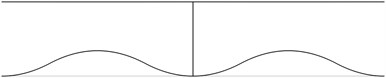
e)

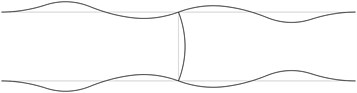
f)

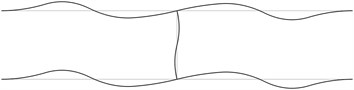
g)

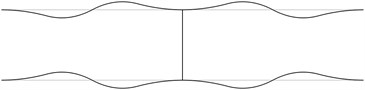
h)

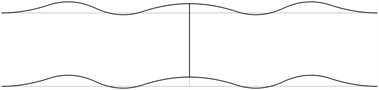
i)

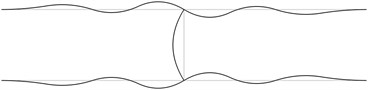
j)

3.1. Model for the analysis of transverse stability of a pipe system with flowing fluid

The finite element of a two dimensional beam representing the pipe in the plane $xOy$ has three nodal degrees of freedom: the displacement in the direction of the $z$ axis denoted as $w$, the rotation about the $x$ axis denoted as ${\theta }_x$ and the rotation about the $y$ axis denoted as ${\theta }_y$.

The rotations about the longitudinal axis of the pipe $s$ and about the axis $t$ perpendicular to $s$ and located in the plane $xOy$ are denoted as ${\theta }_s$ and ${\theta }_t$ and they are related with ${\theta }_x$, ${\theta }_y$ as:

where $ds/d\xi =\sqrt{{\left(dx/d\xi \right)}^2+{\left(dy/d\xi \right)}^2}.$

The stiffness matrix of the pipe for the analysis of transverse stability has the usual form:

where $\left[B\right]=\left[\left[{\stackrel{-}{N}}_1^{\text{'}}\right]+\left[{\stackrel{-}{N}}_3\right]\right].$

The supplementary stiffness matrix of the model of a pipe for the analysis of transverse stability because of the motion of the fluid in it has the form:

3.2. Analysis and measurement of transverse stability of a pipe system with flowing fluid

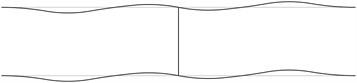
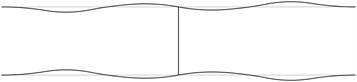
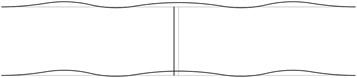
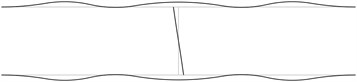
The displacement in the direction of the $z$ axis is represented in the normal direction to the pipe in the plane $xOy$. The first transverse stability eigenmodes are presented in Fig. 2. The fifth and the sixth eigenmodes correspond to the same eigenvalue.

From the presented images of deflections the locations of measurement devices may be chosen.

Fig. 2The first transverse stability eigenmodes of the pipe system: a) the first eigenmode, b) the second eigenmode, …, j) the tenth eigenmode

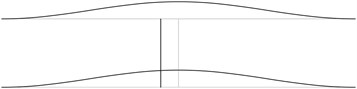
a)

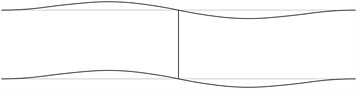
b)

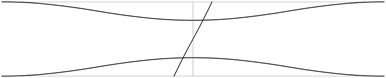
c)

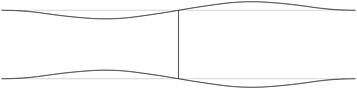
d)

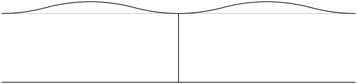
e)

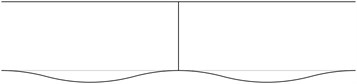
f)

g)

h)

i)

j)