Research of dynamic effects in the process of operation of linear comparator

1. Introduction

Vibration measurements are widely applied in the evaluation or monitoring of measurement systems, the state of machinery and aggregates. Monitoring of measurement parameters and evaluation of their change in time, as well as taking appropriate actions according to the results of measurements helps to evaluate and remove sources of errors. The vibration measurement system performs these functions. Reliability of vibration measurement system in this case is understood as the probability of erroneous decision making, which it is necessary to minimize. This can be achieved by analyzing the factors affecting reliability.

The aim of the work is to create research methodology of evaluating and estimating of dynamic errors of precise comparator, and to investigate the influence of vibrations to the reading accuracy of the comparator with an error and uncertainty estimates. In order to reach the aims of the work it is necessary to solve these tasks:

• On the basis of scientific-technical literature to systematize all the knowledge in this field.

• To form dynamic and mathematical models of precise length measurement comparator system and to perform system modeling based on the experimentally found coefficients.

• To analyze dynamic errors of inherent reading, which are emerging because of the effects of vibrations, and to anticipate the compensation facilities of these errors.

•To investigate experimentally the impact of the results of vibration measurements at different measurement speeds, causing external excitation to the system and measuring vibrations at the time of calibration in order to determine the relationship between the vibration and accuracy of calibration.

• To establish dynamic errors and the methodology of assessment of uncertainty of results of vibration measurements.

Methodology of research includes carried out theoretical studies based on the theoretical mechanics, the vibration theory and the theory of measurements, using analytical, empirical and numerical research methods. The software “Matlab”, “Pulse” and “Origin” were used in the process of investigations.

Experimental material consists of data of the vibration measurement systems. The experiments were made at JSC Precizika Metrology in the Laboratory of Precision Line Scale Comparator. For measurement of parameters of vibrations measurement gauges produced by Bruel & Kjaer and Hottiger were used.

As a result of the performed research work the following new measurement results for the engineering science were obtained:

• The research methodology of dynamic errors of the comparator was created and consistent patterns of arising dynamic errors were determined (using the analytical, engineering and physical models), they enable to investigate precise system errors, resulting due to vibrations.

• The influences of the excitation and parameters of the dynamic system to the errors of calibration were determined.

Following the analysis of sources of literature and research of a number of theoretical and physical models, as well as the study of modern high-tech possibilities, comparator inherent errors arising from the influence of vibrations caused by many physical phenomena were determined: such as the vibration source of environment and the vibration source of the comparator.

The data obtained were used to assess the uncertainty of the results of vibration measurements and to investigate the errors, resulting from the influence of vibrations.

Length calibration systems and their errors were investigated. The length measurement calibration systems and their errors are analyzed, review of evaluation methodologies of calibration uncertainty is made, and evaluation of uncertainty of results of vibration measurements is performed.

According to the literature review it was found that for dynamic research of calibration systems little attention was devoted, especially:

• To set the dynamic errors of calibration system which has influence on quality of calibration, and to calculate their influence to quality of calibration [1-3];

• Research of system dynamics [4-6];

• Research of experimental line scale gage calibration in dynamic mode of vibration and assessment of uncertainty of calibration [7-9];

• The assessment of uncertainty of results of vibration measurements.

The status of current investigations of line scale comparators and related problems are presented in [10-16].

2. Dynamics of the line scale comparator

2.1. Description of the investigated line scale comparator

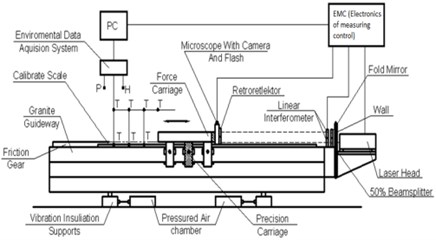
The investigated precise line gauge calibration comparator (Fig. 1) consists of nine main parts: laser type interferometer, gauge of measured environmental parameters, microscope with CCD camera, drive system, controller, data gathering and processing computer, correction system, granite guide ways, the carriage system consisting from the force carriage and the precise carriage.

Fig. 1The scheme a) and general view b) of the length measurement comparator

a)

b)

All parts of the length measurement comparator are interrelated and synchronized. The base part of the comparator is the massive fine structure granite frame of the 4 m length with guide ways, which in the horizontal plane is placed on four pneumatic supports. Those supports perform the damping of high frequency oscillations. The carriage system moves along the frame guide ways. The carriage system is designed in such a way, that carriages are located on stiffly mounted aerostatic supports, which are preloaded with the help of supports mounted in the opposite sides. The mounting of the supports is designed in such a way that they have a possibility to spring. This enables to adjust required small clearances in aerostatic supports and to increase the rigidity of the structure.

2.2. Dynamic model of the investigated line scale comparator

It was concluded that the investigated line scale comparator may be represented by the dynamic models of the total comparator and separately of the carriage. Comparator dynamic model is shown in Fig. 2.

Fig. 2Dynamic model of the comparator for precise length measurment

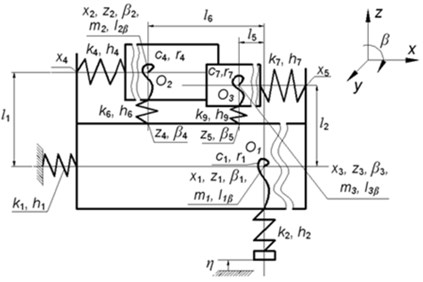
a) The view in the $zx$ plane

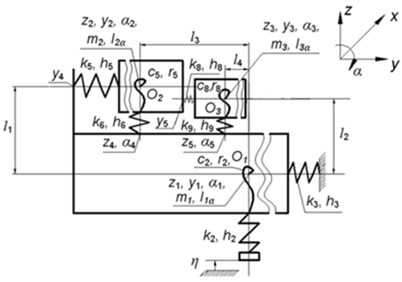
b) The view in the $zy$ plane

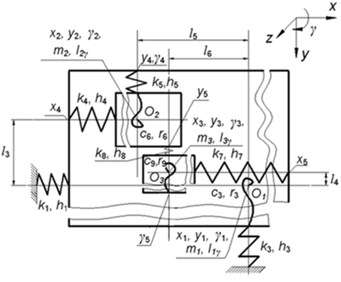
c) The view in the $yx$ plane

Explanations of notations used in Fig. 2: $O_1$, $O_2$, $O_3$ are origins of coordinate systems of separate subsystems of the model, they coincide with mass centres of corresponding parts; $m_1$, $m_2$, $m_3$ are their mass centers; $I_{1j}$, $I_{2j}$, $I_{3j}$ are their moments of inertia, where $j$ corresponds to twisting angles $\alpha$, $\beta$, $\gamma$; $k_n$ are coefficients of rigidity according to the linear axes of motion ($n=$ 1, ..., 9); $c_n$ are coefficients of rigidity according to the angular motion coordinates ($n=$ 1, ..., 9); $h_n$ are damping coefficients according to the linear axes of motion ($n=$ 1, ..., 9); $r_n$ are damping coefficients for angular motions ($n=$ 1, ..., 9); $\eta$ expresses the kinematical excitation function (oscillations of the foundation).

The precision length comparator is a complicated mechatronic system, for correct evaluation of which dynamic researches should be performed. In order to derive differential equations of this system it is recommended to use the Lagrange equations of the second type.

The mathematical model of the total system will compose the system of differential equations of the second order and algebraic constraint equations. The differential equations are represented in the form:

1

$\left[M\right]\left\{\ddot{\delta }\left(t\right)\right\}+\left[C\right]\left\{\dot{\delta }\left(t\right)\right\}+\left[K\right]\left\{\delta \left(t\right)\right\}=\left\{F\left(t\right)\right\},$

where $\left[M\right]$, $\left[C\right]$, $\left[K\right]$ are matrices of inertia, damping and rigidity; $\left\{\delta \left(t\right)\right\}$, $\left\{\dot{\delta }\left(t\right)\right\}$, $\left\{\ddot{\delta }\left(t\right)\right\}$ are vectors of generalized displacements, velocities and accelerations, $\left\{F\left(t\right)\right\}$ is the vector of generalized external forces.

For the investigated system the matrixes $\left[M\right]$, $\left[C\right]$, $\left[K\right]$ are symmetric and non negative definite and the matrix $\left[M\right]$ is positive definite.

2.4. Results of investigation of dynamics of the comparator

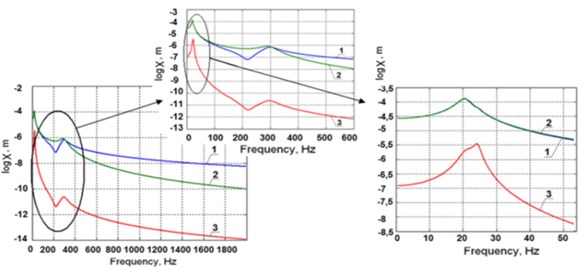
The system response to the most important excitation – the force added to the force carriage, is shown in Fig. 3(a). There are seen two zones of resonances on the frequency curves: the zone of 20-25 Hz and the zone of 280-310 Hz. The error depends on the actual amplitude of the excitation force. In the investigation and presented results it is assumed as the unit force.

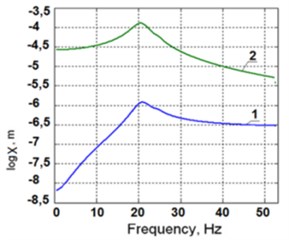
Fig. 3Amplitude frequency response to the excitation added to the force carriage in the y2 direction a): of the precise carriage along the coordinate y3 (1), of the force carriage along the coordinate y2 (2), of the frame along the coordinate y1 (3); amplitude frequency response to the excitation added to the force carriage in the y2 direction b)

a)

b)

Amplitude frequency characteristics of oscillations of the force in the carriage with respect to the precise one (1) and of oscillations of the frame with respect to the precise carriage (2) are shown in Fig. 3(b) (of the force in the carriage with respect to the precise carriage, $y_2$-$y_3$ (1), of the precise carriage with respect to the frame, $y_3$-$y_1$ (2)).

In the picture two zones of resonances on the frequency curves can be seen: the zone of 20-25 Hz and the zone of 280-310 Hz. The error depends on the actual amplitude of the excitation force. Here it is assumed as the unit force. Modes of oscillations falling into these zones are shown in Fig. 3(a). It is seen, that the oscillations along the coordinates $y_2$ and $y_3$ are taking place at these frequencies in a counteraction manner.

3. Experimental dynamic research of line scale comparator

The aim of these studies is to determine calibration errors caused by the mechanical instability of the system. They occur in cases when:

• the distance between the point where the optical axis of the microscope intersects with the plane of the scale lines and carriage point displacement of which is measured by laser interferometer changes;

• the carriage speed changes in the direction of measurement of motion during photographic registration of lines.

In order to clarify reasons causing these factors and the degree of their impact to the positioning error the following studies of dynamic stability of mechanical system of the comparator have been made:

• vibrations of the concrete foundation in horizontal and vertical directions which excite vibrations of the comparator were specified (more exactly);

• vibrations of the comparator base – granite guide ways in the direction along guide ways and in the vertical direction were specified (more exactly);

• vibrations of the characteristic points of the carriage under excitations of impact type were investigated;

• vibrations of the carriage point where the microscope is attached, as well as relative vibrations of the microscope and mirror of the laser interferometer, which is fixed to the carriage under the following conditions:

a) all pneumatic systems are switched off;

b) pneumatic vibration insulation supports are switched off;

c) all pneumatic systems are switched on;

d) measurements are performed on the working speed, smaller speed than the working speed, faster speed than the working speed;

e) motion is carried without electrical actuators.

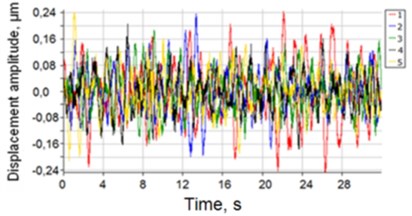
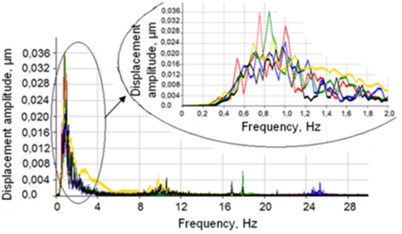
Fig. 4Graphs of absolute vibrations a) of point D and vibration spectrum b) in the longitudinal direction: 1 – all pneumatic systems and the drive are switched off; 2 – all pneumatic systems are switched off and the drive is switched on; 3 – vibration insulation supports are switched on, but no air is in the air bearings of the carriage and the drive is switched on; 4 – all pneumatic systems and the drive are switched on; 5 – all pneumatic systems are switched on and the drive is switched off

a)

b)

Velocities of carriage oscillations at different speeds of movement were investigated: with the aim to investigate the influence of the drive to the mechanical system of the comparator for length measurement, the drive mounting position was replaced and the friction drive was changed into the rope drive.

The results of measurements and analysis of the vibrations of the carriage in the static state are shown in Fig. 4, and the obtained results provide the basis for design of the investigated system.

When the carriage moves with the working speed of 3 mm/s and less, the obtained results are given in Fig. 5 (1 – carriage speed 1 mm/s, 2 – carriage speed 2 mm/s, 3 – carriage speed 3 mm/s).

Fig. 5Graphs of relative vibrations of the laser microscope with respect to the mirrors of the laser interferometer a) and spectrum of vibrations b)

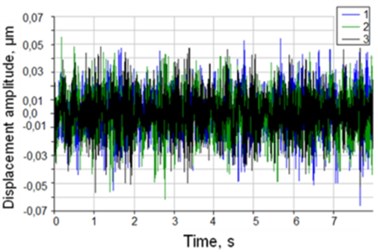
a)

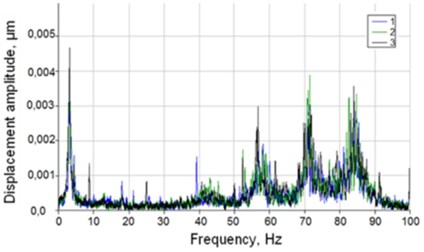
b)

4. Conclusions

1. On the basis of the references about qualitative analysis of precise line scale measuring comparators, it can be concluded that the influence of dynamics to the accuracy of calibration of the comparator is insufficiently researched. Particularly error components due to vibrations and its weight are not evaluated in the total uncertainty budget.

2. After creating the mathematical model for the comparator dynamics and after performing the computer experiments according to the proposed model and verification of it by realistic tests it was shown:

2.1. It was determined that when the seismic excitation from the ground acts to the comparator with realistic values of oscillation amplitudes, values of vibration amplitudes are small (till 0.1 µm) and they do not have a significant impact on the dynamic performance characteristics of the system.

2.2. It is found that the oscillations of the precision and force carriages at resonant frequencies 24 Hz and 296 Hz are taking place in opposite directions and they can be harmful.

3. It was determined experimentally that the biggest influences to generation of vibrations have: the design of the carriages of the comparator and of the drive submitting the motion to the force carriage.

4. It is found that the influence of vibrations to the calibration error is smallest, when the speed of carriage of the comparator is 3 mm/s.

5. Regularities of the occurrence of dynamic errors associated with the position of the drive mounting were clarified: after replacing the drive system to the granite guide ways, frequency of absolute vibrations of the system decreases from 10 Hz till 3 Hz, at which the amplitude of the dominant vibrations is the highest.