Dynamic characteristic analysis of two-stage quasi-zero stiffness vibration isolation system

Chai, Kai; Yang, Qing-chao; Lou, Jing-jun

Vibroengineering Procedia

Browse Procedia

Published: 08 December 2016

Check for updates

Dynamic characteristic analysis of two-stage quasi-zero stiffness vibration isolation system

Kai Chai¹

Qing-chao Yang²

Jing-jun Lou³

¹College of Power Engineering, Naval University of Engineering, Wuhan, China

^{2, 3}National Key Laboratory on Ship Vibration and Noise, Naval University of Engineering, Wuhan, China

Corresponding Author:

Kai Chai

Cite the article Download PDF

Downloads 1528

Abstract

A novel two-stage quasi-zero stiffness (QZS) vibration isolator was proposed for the purpose of low-frequency vibration isolation. Firstly, the dynamic model of the vibration isolation system was established; furthermore, the force transmissibility of the system under harmonic force excitation was derived by the averaging method; finally, the effects on the vibration isolation performance caused by excitation amplitude, mass ratio and damping ratio were discussed. Results show that, compared with the corresponding two-stage linear system, two-stage QZS system not only has better isolation performance, but also possesses a wider range of isolation frequency provided that the excitation amplitude, mass ratio and damping ratio is appropriate.

1. Introduction

Quasi-zero stiffness (QZS) isolator can obtain zero stiffness at the static equilibrium position by connecting a positive stiffness element in parallel with a negative stiffness element [1]. By reasonably selecting the geometry and stiffness parameters of the negative stiffness institutions, the vibration isolation system can support a large load statically while have low-frequency vibration isolation performance. The combination of positive and negative stiffness device possesses the characteristics of high-static-low-dynamic stiffness and can ensure that the system natural frequency is very low at small deformation [2]. Therefore, scholars have conducted in-depth research on isolator principle [3], structure design [4], properties analysis [5] and engineering application [6] of QZS, which is widely used in precision instrument isolation, bridge and house anti-earthquake, high-speed vehicle vibration reduction, marine machinery noise cancellation and other fields.

With the development of science and technology, the request of stability for the work environment of precision equipment is more and more strictly. Conventional single-stage linear or QZS vibration isolation system cannot meet requirements of industry [7, 8]. When the excitation frequency is greater than $\sqrt{2}$ times the natural frequency, vibration decay ratio is proportional to $ω^{- 2}$ in the single-stage system, while that is proportional to $ω^{- 4}$ in the two-stage system. So rigid two-stage isolation system can replace soft single-stage isolation system, which not only has good isolation effect, but also takes into account the load-bearing capacity and stability. Although the two-stage isolator is better isolation performance than the single-stage isolator, but the former has one more resonance peak and longer resonance time. To play the single QZS advantages, also take large vibration decay ratio of two-stage isolation system into consideration. Two-stage QZS vibration isolator was proposed, whose effects on the vibration isolation performance caused by excitation amplitude, mass ratio and damping ratio were studied.

2. Mechanical model of QZS vibration isolation system

Fig. 1 shows a typical QZS system. The system consists of a suspended mass $m$ with a vertical spring and two identical oblique springs.

The force-deflection in the vertical direction is given by:

1

F_{v} = k_{v} x + 2 k_{h} (1 - \frac{l_{0}}{\sqrt{x^{2} + l^{2}}}) x,

where $l_{0}$ is the free length of horizontal springs and $l$ is length in the horizontal position. $x$ is the displacement deviation from equilibrium position. The stiffness of oblique spring is $k_{h}$ and the stiffness of horizontal spring is $k_{h}$ .

Eq. (1) can be written in non-dimensional form as:

2

\hat{f} = \frac{F_{v}}{k_{v} x_{0}} = \hat{x} + 2 \hat{k} (1 - \frac{1}{\sqrt{({\hat{x}}^{2} (1 - {\hat{l}}^{2}) + {\hat{l}}^{2}}}) \hat{x},

where $\hat{x} = x / x_{0}$ , $\hat{l} = l / l_{0}$ and $\hat{k} = k_{h} / k_{v}$ . Using the Maclaurin-series expansion to the third order for small $\hat{x}$ , then Eq. (2) approximates to:

3

\hat{f} = k_{a} \hat{x} + k_{b} {\hat{x}}^{3},

where $k_{a} = 1 - 2 \hat{k} (1 - \hat{l}) / \hat{l}$ and $k_{b} = \hat{k} (1 - {\hat{l}}^{2}) / {\hat{l}}^{3}$ .

Fig. 1Schematic diagram of the QZS vibration isolation system

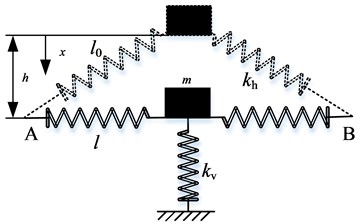
Fig. 2Schematic of a two-stage QZS system

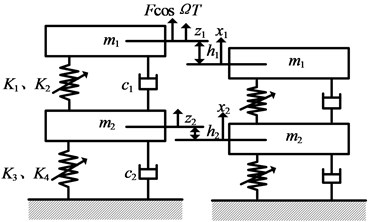
3. Two-stage QZS vibration isolation system

The two-stage QZS system is shown in Fig. 2.

It is subject to external harmonic force excitation $F c o s Ω T$ . The upper QZS isolator stiffness coefficient is $K_{1}$ , $K_{2}$ and damping coefficient is $c_{1}$ . The lower QZS isolator stiffness coefficient is $K_{3}$ , $K_{4}$ and damping coefficient is $c_{2}$ . $z_{1}$ and $z_{2}$ are the displacement of the vibration object and the middle inertia block when the respective spring in a natural state. $m_{1}$ and $m_{2}$ are the mass of vibration object and middle inertia block respectively.

Provided that only consider the vertical direction of movement, dynamic equation of two-stage QZS system is established based on Newton’s second law:

4

\{\begin{array}{l} m_{1} {\ddot{z}}_{1} + c_{1} ({\dot{z}}_{1} - {\dot{z}}_{2}) + K_{1} (z_{1} - z_{2}) + K_{2} (z_{1} - z_{2})^{3} = F c o s (Ω T) - m_{1} g, \\ m_{2} {\ddot{z}}_{2} - c_{1} ({\dot{z}}_{1} - {\dot{z}}_{2}) - K_{1} (z_{1} - z_{2}) - K_{2} (z_{1} - z_{2})^{3} + c_{2} {\dot{z}}_{2} + K_{3} z_{2} + K_{4} {z_{2}}^{3} = - m_{2} g . \end{array}

For clarity of analysis, the parameters $Ω_{0} = \sqrt{K_{1} / m_{1}}$ , $z_{1} = X_{1} \sqrt{K_{1} / K_{2}}$ , $z_{2} = X_{2} \sqrt{K_{1} / K_{2}}$ , $T = Ω_{0} t$ are introduced. Eq. (4) can be written in non-dimensional form as:

5

\{\begin{array}{l} {\ddot{X}}_{1} - ξ_{1} ({\dot{X}}_{2} - {\dot{X}}_{1}) - (X_{2} - X_{1}) - (X_{2} - X_{1})^{3} = f c o s (ω t) - G, \\ w {\ddot{X}}_{2} + ξ_{1} ({\dot{X}}_{2} - {\dot{X}}_{1}) + (X_{2} - X_{1}) + (X_{2} - X_{1})^{3} + ξ_{2} {\dot{X}}_{2} + k_{1} X_{2} + k_{2} {X_{2}}^{3} = - w G, \end{array}

where $ξ_{1} = c_{1} / \sqrt{K_{1} m_{1}}$ , $f = F / K_{1} \sqrt{K_{2} / K_{1}}$ , $G = m_{1} g / K_{1} \sqrt{K_{2} / K_{1}}$ , $k_{1} = K_{3} / K_{1}$ , $k_{2} = K_{4} / K_{2}$ , $k_{3} = K_{2} / K_{1}$ , $ξ_{2} = c_{2} / \sqrt{K_{1} m_{1}}$ , $w = m_{2} / m_{1}$ , $ω = Ω_{0} Ω$ .

In order to analyze conveniently, the first and second equation of Eq. (5) are added, which can make stiffness coupling change into inertia coupling. The gravity term in Eq. (5) can be eliminated by using coordinate transform. Introducing $X_{1} = Z_{1} - h_{1}$ , $X_{2} = Z_{2} - h_{2}$ , $H = h_{1} - h_{2}$ , $x_{1} = Z_{2} - Z_{1}$ , $x_{2} = Z_{2}$ , Eq. (5) can be transferred as:

6

\{\begin{array}{l} {\ddot{x}}_{2} - {\ddot{x}}_{1} - ξ_{1} {\dot{x}}_{1} - (1 + 3 H^{2}) x_{1} - 3 H {x_{1}}^{2} - {x_{1}}^{3} = f c o s (ω t), \\ (1 + w) {\ddot{x}}_{2} - {\ddot{x}}_{1} + ξ_{2} {\dot{x}}_{2} + (k_{1} + 3 k_{2} {h_{2}}^{2}) x_{2} - 3 k_{2} h_{2} {x_{2}}^{2} + k_{2} {x_{2}}^{3} = f c o s (ω t), \end{array}

where $H + H^{3} = G$ , $k_{1} h_{2} + k_{2} {h_{2}}^{3} = (w + 1) G$ .

Eq. (6) in matrix form is:

7

M \ddot{X} + C \dot{X} = F,

where:

M = [\begin{array}{l} - 1 & 1 \\ - 1 & 1 + w \end{array}], C = [\begin{matrix} - ξ_{1} & 0 \\ 0 & ξ_{2} \end{matrix}], X = [\begin{array}{l} x_{1} \\ x_{2} \end{array}],

F = [\begin{matrix} f c o s (ω t) + (1 + 3 H^{2}) x_{1} + 3 H {x_{1}}^{2} + {x_{1}}^{3} \\ f c o s (ω t) - (k_{1} + 3 k_{2} {h_{2}}^{2}) x_{2} + 3 k_{2} h_{2} {x_{2}}^{2} - k_{2} {x_{2}}^{3} \end{matrix}] .

By the averaging method, suppose steady-state response solution of the above system as:

8

\{\begin{array}{l} X = U c o s (ω t) + V s i n (ω t), \\ X^{'} = - ω U c o s (ω t) + ω V s i n (ω t), \end{array}

where $U = {[U_{1}, U_{2}]}^{T}$ and $V = {[V_{1}, V_{2}]}^{T}$ change slowly with time. Differentiate the first equation of Eq. (8) with respect to $t$ and eliminate the second equation of Eq. (8):

9

U' c o s (ω t) + V' s i n (ω t) = 0 .

Differentiate the second equation of Eq. (8) with respect to $t$ and take it into Eq. (7):

10

(ω M V^{'} - ω^{2} M U + ω C V) c o s (ω t) - (ω M U^{'} + ω^{2} M V + ω C U) s i n (ω t) = F .

Based on Eqs. (9) and (10), it can be inferred as:

11

\{\begin{array}{l} ω M U^{'} = - F s i n (ω t) + (- ω^{2} M U + ω C V) c o s (ω t) s i n (ω t) - (ω^{2} M V + ω C U) s i n^{2} (ω t), \\ ω M V^{'} = F c o s (ω t) + (ω^{2} M V + ω C U) s i n (ω t) c o s (ω t) + (ω^{2} M U - ω C V) c o s^{2} (ω t) . \end{array}

Note that, $U$ and $V$ are the slowly changing function of time. The right side of Eq. (11) can be approximately represented with the average value of $(ω t)$ in a period. Provided that $U$ and $V$ remain unchangeable in a period, average equation can be obtained as:

12

\{\begin{array}{l} ω M U^{'} = \int_{0}^{2 π} [\begin{matrix} - F \sin (ω t) + (- ω^{2} M U + ω C V) \cos (ω t) \sin (ω t) \\ - (ω^{2} M V + ω C U) s i n^{2} (ω t) \end{matrix}] / 2 π d ω t, \\ ω M V^{'} = \int_{0}^{2 π} [\begin{matrix} F \cos (ω t) + (ω^{2} M V + ω C U) \sin (ω t) \cos (ω t) \\ + (ω^{2} M U - ω C V) c o s^{2} (ω t) \end{matrix}] / 2 π d ω t . \end{array}

According to the orthogonality of trigonometric function, Eq. (12) can be simplified as:

13

\{\begin{array}{l} ω M U^{'} = - \frac{1}{2} (ω^{2} M V + ω C U) - \frac{1}{2} (\begin{array}{l} Q_{1} \\ Q_{2} \end{array}), \\ ω M V^{'} = \frac{1}{2} (ω^{2} M U - ω C V) + \frac{1}{2} (\begin{array}{l} Q_{3} + f \\ Q_{4} + f \end{array}), \end{array}

14

Q_{1} = (1 + 3 H^{2} + \frac{3 U_{1}^{2}}{4}) V_{1} + \frac{3 V_{1}^{3}}{4}, Q_{2} = (- k_{1} - 3 k_{2} {h_{2}}^{2} - \frac{3 k_{2} U_{2}^{2}}{4}) V_{2} - \frac{3 V_{1}^{3}}{4},

Q_{3} = (1 + 3 H^{2} + \frac{3 V_{1}^{2}}{4}) U_{1} + \frac{3 U_{1}^{3}}{4}, Q_{4} = (- k_{1} - 3 k_{2} {h_{2}}^{2} - \frac{3 k_{2} V_{2}^{2}}{4}) U_{2} - \frac{3 U_{2}^{3}}{4} .

Then, the response of system is the solution of following equation:

15

\{\begin{array}{l} - ω^{2} V_{1} + ω^{2} V_{2} - ξ_{1} ω U_{1} + Q_{1} = 0, \\ - ω^{2} V_{1} + (1 + w) ω^{2} V_{2} + ξ_{2} ω U_{2} + Q_{2} = 0, \\ - ω^{2} U_{1} + ω^{2} U_{2} + ξ_{1} ω V_{1} + Q_{3} + f = 0, \\ - ω^{2} U_{1} + (1 + w) ω^{2} U_{2} + ξ_{2} ω V_{2} + Q_{4} + f = 0 . \end{array}

The force transmitted to the base includes elastic restoring force and damping force of the lower vibration isolator, which can be expressed as:

16

f_{a} = ξ_{2} {\dot{x}}_{2} + (k_{1} + 3 k_{2} {h_{2}}^{2}) x_{2} - 3 k_{2} h_{2} {x_{2}}^{2} + k_{2} {x_{2}}^{3} .

Substitute Eq. (6) in Eq. (14) and neglect higher harmonics:

17

f_{a} = f_{b} c o s (ω t) + f_{c} s i n (ω t) + f_{d},

where:

f_{b} = (k_{1} + 3 k_{2} {h_{2}}^{2}) U_{2} + ω ξ_{2} V_{2} + \frac{3 k_{2} U_{2} ({U_{2}}^{2} + {V_{2}}^{2})}{4},

f_{c} = (k_{1} + 3 k_{2} {h_{2}}^{2}) V_{2} - ω ξ_{2} U_{2} + \frac{3 k_{2} V_{2}}{4} ({V_{2}}^{3} + {U_{2}}^{2}), f_{d} = - \frac{3 k_{2} h_{2} ({U_{2}}^{2} + {V_{2}}^{2})}{2} .

Force transmissibility of two-stage QZS system is calculated as:

18

T_{f} = (\sqrt{{f_{b}}^{2} + {f_{c}}^{2}} + |f_{d}|) / f .

As a comparison, the two oblique springs are removed.

By successively applying the same procedure as for the model of equivalent two-stage linear system, the response of the system is the solution of Eq. (15), where

19

Q_{1} = 3 V_{1} / 4, Q_{2} = k_{1} V_{2}, Q_{3} = U_{1}, Q_{4} = k_{1} U_{2} .

Similarly, the force transmissibility of two-stage linear system can be founded:

20

T_{f l} = \sqrt{(4 w^{2} {ξ_{2}}^{2} {V_{2}}^{2} + {k_{1}}^{2}) ({U_{2}}^{2} + {V_{2}}^{2})} / f .

4. Influence of the system parameters on force transmissibility

As discussed above, force transmissibility is closely related to $f$ , $w$ and $ξ$ . Next, the effects of different system parameters on force transmissibility of two-stage QZS system are investigated by controlling variables method. The Force transmissibility of two-stage linear system at the same condition is also plotted together to compare the isolation performance of two systems. All the force transmissibility results are plotted in dB, i.e. as $20 l o g_{10} T$ .

Fig. 3 shows the force transmissibility of system under different $f .$ Two-stage linear system are not influenced by the $f$ . However, for the two-stage QZS system, two order resonant frequencies and transmissibility peaks increase with the rising of $f$ . The less the $f$ is, the better the isolation performance of two-stage QZS system compared with the two-stage linear system. Fig. 4 shows the force transmissibility of system under different $w$ , for the two-stage linear system, two order resonant frequencies increase with the rising of $w$ , the transmissibility of the first order resonant frequency decreases, while the transmissibility of the second order resonant frequency increases. For the two-stage QZS system, the first order resonant frequency transmissibility decreases with the rising of $w$ , while the second resonant order frequency and transmissibility increases with the rising of $w$ . Which indicates that the isolation bandwidth broadens and isolation performance near the second order resonant frequency weakens with the rising of $w$ .

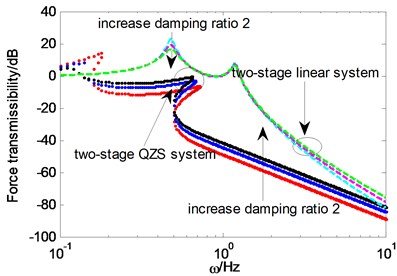
The force transmissibility curves of system under different $ξ$ are illustrated in Fig. 5 and Fig. 6 respectively. Two order resonant frequencies of two-stage linear system are not influenced by the $ξ_{1}$ , while the peaks of corresponding force transmissibility reduce. Force transmissibility of system under different $ξ_{1}$ is shown in Fig. 5. The resonance branch of the two-stage QZS system shortens and the peaks of corresponding force transmissibility reduce with the rising of $ξ_{1}$ . But the isolation performance will decrease when the excessive damping ratio. Force transmissibility of system under different $ξ_{1}$ is shown in Fig. 6. Two order resonant frequencies increase with the rising of $ξ_{2}$ . The transmissibility of the first order resonant frequency decreases, while the transmissibility of the second order resonant frequency increases, which indicates that the isolation performance near the second order resonant frequency weakens with the rising of $ξ_{2}$ .

Fig. 3Force transmissibility under different f

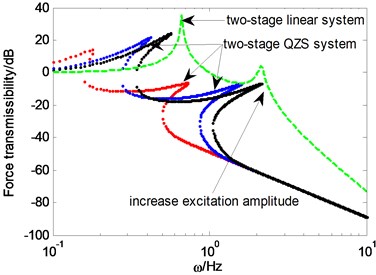
Fig. 4Force transmissibility under different w

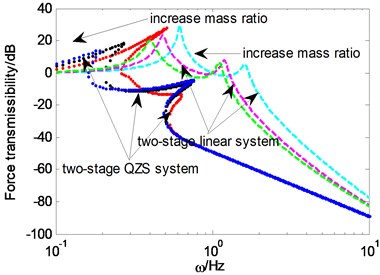
Fig. 5Force transmissibility under different ξ1

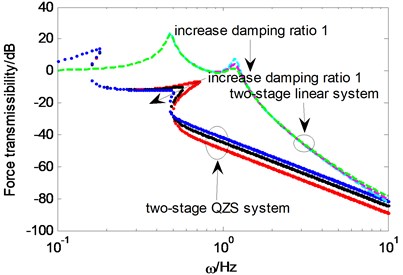
Fig. 6Force transmissibility under different ξ2

5. Conclusions

In this study, a novel two-stage quasi-zero stiffness vibration isolator was presented. The conclusions were summarized as follows:

1) The dynamic models of two-stage QZS and linear vibration isolation system were established. The force transmissibility under harmonic force excitation was derived by using the averaging method.

2) Decrease the excitation amplitude and increase the mass ratio as well as damping ratio properly, which can broaden the isolation bandwidth, increase the vibration decay ratio and enhance the isolation performance of two-stage QZS system.

3) Compared to the corresponding two-stage linear system, the two-stage QZS system not only has smaller initial isolation frequency, wider isolation band and better isolation performance, but also possesses excellent load-bearing capacity and stability.

References

Zhu Tao, Cazzolato Benjamin, Robertson William S. P., et al. Vibration isolation using six degree-of-freedom quasi-zero-stiffness magnetic levitation. Journal of Sound and Vibration, Vol. 358, 2015, p. 48-73.

Search CrossRef
Zou Keguan, Nagarajaiah Satish Study of a piecewise linear dynamic system with negative and positive stiffness. Communications in Nonlinear Science and Numerical Simulation, Vol. 22, 2015, p. 1084-1101.

Search CrossRef
Ma Yanhui, He Minghua, Shen Wenhou, et al. A planar shock isolation system with high-static-low-dynamic-stiffness characteristic based on cables. Journal of Sound and Vibration, Vol. 358, 2015, p. 267-284.

Search CrossRef
Gatti Gianluca, Kovacic Ivana, M. J. Brennan. On the response of a harmonically excited two degree-of-freedom system consisting of a linear and a nonlinear quasi-zero stiffness oscillator. Journal of Sound and Vibration, Vol. 329, 2010, p. 1823-1835.

Search CrossRef
Lan Chao-Chieh, Yang Sheng-An, Wu Yi-Syuan Design and experiment of a compact quasi-zero-stiffness isolator capable of a wide range of loads. Journal of Sound and Vibration, Vol. 333, 2014, p. 4843-4858.

Search CrossRef
Liu Xingtian, Huang Xiuchang, Hua Hongxing On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector. Journal of Sound and Vibration, Vol. 332, 2013, p. 3359-3376.

Search CrossRef
Zhou Jiaxi, Wang Xinlong, Xu Daolin, et al. Nonlinear dynamic characteristics of quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms. Journal of Sound and Vibration, Vol. 346, 2015, p. 53-69.

Search CrossRef
Sun Xiuting, Jing Xingjian Multi-direction vibration isolation with quasi-zero stiffness by employing geometrical nonlinearity. Mechanical System and Signal Processing, Vol. 62, Issue 63, 2015, p. 149-163.

Search CrossRef

About this article

Received

31 August 2016

Accepted

03 September 2016

Published

08 December 2016

SUBJECTS

Mechanical vibrations and applications

Keywords

two-stage quasi-zero stiffness

the averaging method

force transmissibility

vibration isolation system

Acknowledgements

The authors gratefully acknowledge the support for this work by the National Natural Science Foundation of China (NSFC) under Grant No. 51579242 and No. 51509253.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.