Abstract
This paper presents a rolling bearing fault diagnosis approach based on the combination of Ensemble Empirical Mode Decomposition (EEMD), Information Entropy (IE) and Random Forests (RF). The horizontal and vertical vibration signals of the bearings are utilized as the input of the method. First, the signals, after preprocess, are decomposed into certain number of intrinsic mode functions (IMF) using EEMD. Second, the IEs of the IMFs are calculated as the features for further fault diagnosis. Third, the selected features are adopted to train the random forests model using 10-fold cross validation. Fourth, the trained RF model is used to conduct bearing fault diagnosis. To verify the effectiveness of the proposed approach, three types of faults including inner-ring fault, outer-ring fault and rolling element fault are considered and data from two individual experiments are used. The results demonstrate that the approach has desirable diagnostic performance both for cylindrical roller bearing and deep groove ball bearing.
1. Introduction
Rolling bearings are the one of the most commonly used components in rotational machines and their failure may lead to huge economic losses, environment pollution and human casualties. Hence, the fault diagnosis of the rolling bearing is vital to guarantee the smooth and safe functioning of the mechanical systems.
A great deal of researches on vibration-based diagnostics of rolling bearings have prompted and several powerful diagnostic methods are available [1]. As an example, the world has witnessed a tremendous growth in the theory and practice of empirical mode decomposition (EMD) on bearing fault diagnosis [2-5]. By breaking down vibration signals into various components, EMD has done well in bearing fault diagnosis until the vibration signals are corrupted by intermittency, impulse interference and noises which are commonly encountered in bearing fault vibration signals. In order to deal with this problem, EEMD, an improved version of EMD, is adopted in this paper.
Feature extraction, without any questions, is the key part in vibration-signal based bearing fault diagnosis. Traditional time domain statistical parameters such as mean, variance, root mean square value etc. are all easily accessed but not enough to handle severe faults since they can be interfered by random shock [6]. However, entropies as a quantitative metric for time series complexity, have been utilized by many researchers for bearing fault diagnosis and yield more than good results [7-9]. Based on diagnosis effectiveness, this paper chooses information entropy to extract features from the vibration signals.
The kernel of the bearing fault diagnosis is the feature based pattern recognition. A lot of mature pattern recognition algorithms have been successfully applied on bearing fault diagnosis such as artificial neural network (ANN), hidden Markov model (HMM) and support vector machine (SVM) [10-19]. However, the RF invented by Breiman [20] in 2001 is rarely adopted in that field. Hence this paper attempts to utilize RF and test its effectiveness on bearing fault diagnosis.
2. Methodology
2.1. EEMD
Aiming at the illusive component and mode mixing problems, EEMD was developed by Huang [21] as an improved algorithm of EMD. The core of EEMD is to add Gaussian white noise to signals and conduct multiple EMDs respectively so that multiple sets of IMFs will be obtained and the average of them will be determined as the final IMFs. The procedures of EEMD are as follows:
(1) Add Gaussian white noise to original signal to obtain an new signal :
(2) Use EMD to decompose into IMFs:
(3) Repeat step (1) and step (2) times with a different Gaussian white noise every time:
(4) Calculate the ensemble means of corresponding IMFs as the final IMFs:
Thus according to the zero-mean of Gaussian white noise, the original can be presented as:
2.2. IE
Information entropy, proposed by Shannon [22] in 1948, is a metric of information disorder degree. The bigger the information entropy is, the higher the information disorder degree is. And that makes it an ideal feature for bearing fault diagnosis since bearing vibration signals are obviously also a kind of information. The definition of IE is as follows:
Assume a system has several different states , ,…, , and is the probability of state ( 1, 2,…, ) then the information entropy of the system is defined as:
where , and stipulate that when .
2.3. RF
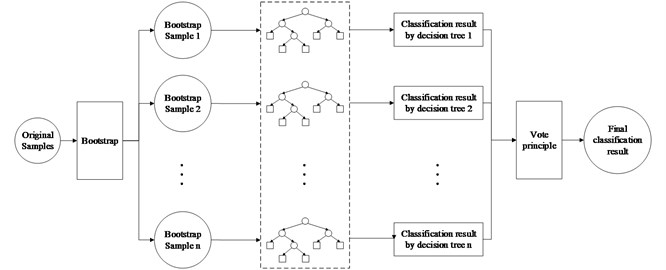
Random forests, invented by Breiman [20], is a statistical-based learning method. Using bootstrap approach it firstly draws multiple bootstrap samples from the original samples. Secondly, the bootstrap samples are used to generate corresponding decision trees. Thirdly, the prediction results given by those decision trees will be synthesized and the final result will be produced by certain principles, mostly the simple majority principle. The schematic diagram of RF is shown in Fig. 1.
A lot of researches have demonstrated that RF occupies at least three advantages, (1) a relatively high prediction accuracy; (2) high tolerability of anomaly data and noise; (3) overfitting can be avoided; Those advantages make it an ideal fault diagnosis model for bearing faults.
Fig. 1The schematic diagram of RF
3. Experiment tests
In order to verify the effectiveness of the proposed method, two individual bearing fault experiments were adopted.
As shown in Fig. 2, the first experiment was originally conducted on rotational machinery fault simulation test bed (QPZZ-II). The sampling frequency is 5120 samples per second and the rotation speed is 1500 revolutions per minute.
Fig. 2Test rig of experiment 1

The test bearings used are cylindrical roller bearing (N205EM HRB CHINA). The inner-ring fault, outer-ring fault and roller element fault are introduced by wire-electrode cutting a crevice on the surface of inner ring, outer ring and one of the roller elements as marked in Fig. 3.
The second experiment is conducted by Case Western Reserve University (CWRU). The test rig, which consists of a 2 horsepower motor (Fig. 3(a)), a torque transducer/encoder (Fig. 3(b)), a dynamometer (Fig. 3(c)) and control electronics (not shown) is shown in Fig. 3. The test bearing used is deep groove ball bearing (6205-2RS JEM SKF), into which inner-ring fault, outer-ring fault and ball fault will be injected. The sampling frequency is 12k samples per second and the rotation speed is 1797 revolutions per minute.
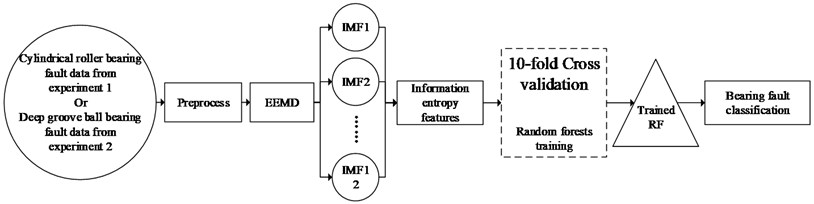
The bearing fault data from both experiment 1 and experiment 2 will be preprocessed first, dividing the whole time-domain signals into ten subgroups. Next, EEMD with different white noise will be applied on those subgroups and henceforth each time 12 IMFs can be obtained. Based on them, information entropies under different faults will be calculated and adopted as features for random forest training. To avoid over-fitting, 10-fold cross validation is considered for RF training. Once the RF model is trained, the bearing fault diagnosis results can be provided and analyzed. The scheme of the method proposed is shown in Fig. 5.
The information entropies of bearings with different faults, shown in Table 1, are quite different, which indicates high potential for faults diagnosis.
The IMFs of bearing with element fault in experiment 1 is shown in Fig. 6.
Fig. 3Faults of inner ring, outer ring and roller element

a)

b)

c)
Fig. 4Test rig of experiment 2

Fig. 5Scheme of the method
As shown in Table 2, the diagnostic accuracy varies from 97.25 % up to 100 %, verifying the effectiveness of the proposed method. EEMD with 0 to be the ratio of the standard deviation of the added noise and that of the input is actually EMD. Obviously, EEMD is better in handling cylindrical roller bearing fault diagnosis that EMD, and when the ratio is 0.15 the diagnostic accuracy is the highest (99 %). However, EEMD with different ratios has no influence on the diagnostic accuracy (constantly 100 %) in experiment 2. Hence EMD is enough for deep groove ball bearing in view of computer resource consumption and time cost reduction.
Fig. 6IMFs of bearing with element fault in experiment 1
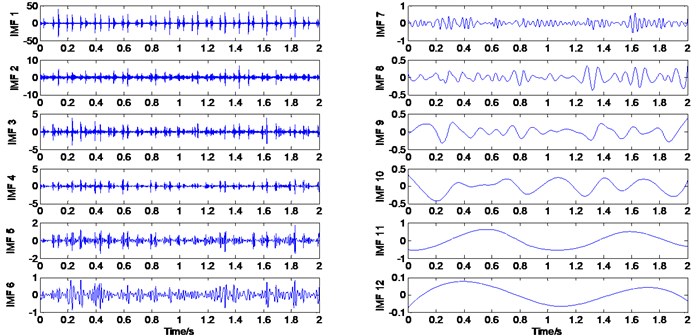
Table 1Information entropies of bearings with different faults
Information entropies | |||||||
Experiment 1 (horizontal direction) | Experiment 2 (Drive end) | ||||||
Normal | Inner-ring fault | Outer-ring fault | Roller element fault | Normal | Inner-ring fault | Outer-ring fault | Roller element fault |
1.7780 | 2.7664 | 1.9032 | 0.5576 | 1.8449 | 1.1220 | 0.2332 | 0.6435 |
Table 2Diagnosis results
Diagnostic accuracy | Ratio of the standard deviation of the added noise and that of the input | |||||
0 (EMD) | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | |
Experiment 1 cylindrical roller bearing | 97.25 % | 98.50 % | 98 % | 99 % | 98.5 % | 98.25 % |
Experiment 2 deep groove ball bearing | 100 % | 100 % | 100 % | 100 % | 100 % | 100 % |
4. Conclusions
Using vibration signals, a method for rolling bearing fault diagnosis based on EEMD, IE and RF is presented in the paper. First, EEMD was utilized to decompose vibration signals from different faults into certain IMFs. Second, IEs are extracted as the fault features from those IMFs. Third, RF model, founded by training on extracted fault features, was used to yield bearing faults diagnosis results. From the experiment results, it can be concluded that:
1) By adding white noise to original vibration signals, EEMD is better than EMD in dealing with cylindrical roller bearing vibration signals.
2) The information entropies obviously varies under different bearing faults, and that indicates IE can be an ideal fault feature for rolling bearing fault diagnosis.
3) The combination of EEMD, IE and RF yields excellent fault diagnosis correct rates for both cylindrical roller bearing and deep groove ball bearing with inner-ring fault, outer-ring fault and rolling element fault.
However both EEMD and RF are computer-resource-consuming algorithms. To obtain a trained model, it usually cost more than 10 to 12 hours depending on hardware specifications. Hence, the method proposed in this paper still has some space to improve to make it more efficient in future work.
References
-
Randall R. B., Antoni J. Rolling element bearing diagnostics – a tutorial. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 485-520.
-
Huang P., Pan Z., Qi X., Lei J. Bearing fault diagnosis based on EMD and PSD. World Congress on Intelligent Control and Automation (WCICA), 2010, p. 1300-1304.
-
Li H., Zheng H. Bearing fault detection using envelope spectrum based on EMD and TKEO. Fuzzy Systems and Knowledge Discovery Fifth International Conference, Vol. 3, 2008, p. 142-146.
-
Miao Q., Wang D., Pecht M. Rolling element bearing fault feature extraction using EMD-based independent component analysis. Prognostics and Health Management IEEE Conference, 2011, p. 1-6.
-
Qiu M. H., Wang Z. Y. Fault diagnosis of bearing based on empirical mode decomposition and decision directed acyclic graph support vector machine. Computational Intelligence and Natural Computing International Conference, 2009, p. 471-474.
-
Kim Paul Y., Cowe I. R. G. A review of rolling element bearing health monitoring. Proceeding of Machinery Vibration Monitoring and Analysis Meeting, 1983.
-
Richman J. S., Moorman J. R. Physiological time-series analysis using approximate entropy and sample entropy. American Journal of Physiology Heart and Circulatory Physiology, Vol. 278, 2000, p. H2039-H2049.
-
Yan R., Gao R. X. Machine health diagnosis based on approximate entropy. IEEE Instrumentation and Measurement Technology Conference, Vol. 3, 2004, p. 2054-2059.
-
Yan R., Gao R. X. Approximate entropy as a diagnostic tool for machine health monitoring. Mechanical Systems and Signal Processing, Vol. 21, 2007, p. 824-839.
-
Yang B. S., Han T., Hwang W. W. Fault diagnosis of rotating machinery based on multi-class support vector machines. Journal of Mechanical Science and Technology, Vol. 19, 2005, p. 846-859.
-
Sanz J., Perera R., Huerta C. Fault diagnosis of rotating machinery based on auto-associative neural networks and wavelet transforms. Journal of Sound and Vibration, Vol. 302, 2007, p. 981-999.
-
Samanta B., Al-Balushi K. R. Artificial neural network based fault diagnostics of rolling element bearings using time-domain features. Mechanical Systems and Signal Processing, Vol. 17, 2003, p. 317-328.
-
Samanta B. Gear fault detection using artificial neural networks and support vector machines with genetic algorithms. Mechanical Systems and Signal Processing, Vol. 18, 2004, p. 625-644.
-
Rojas A., Nandi A. K. Practical scheme for fast detection and classification of rolling-element bearing faults using support vector machines. Mechanical Systems and Signal Processing, Vol. 20, 2006, p. 1523-1536.
-
Purushotham V., Narayanan S., Prasad S. A. N. Multi-fault diagnosis of rolling bearing elements using wavelet analysis and hidden Markov model based fault recognition. NDT&E International, Vol. 38, 2005, p. 654-664.
-
Liu T. I., Ordukhani F., Jani D. Monitoring and diagnosis of roller bearing conditions using neural networks and soft computing. International Journal of Knowledge-based and Intelligent Engineering Systems, Vol. 9, 2005.
-
Lee J. M., Kim S. J., Hwang Y., Song C. S. Diagnosis of mechanical fault signals using continuous hidden Markov model. Journal of Sound and Vibration, Vol. 276, 2004, p. 1065-1080.
-
Fernández-Francos D., Martínez-Rego D., Fontenla-Romero O., Alonso-Betanzos A. Automatic bearing fault diagnosis based on one-class v-SVM. Computers and Industrial Engineering, Vol. 64, 2013, p. 357-365.
-
Castejón C., Lara O., García-Prada J. C. Automated diagnosis of rolling bearings using MRA and neural networks. Mechanical Systems and Signal Processing, Vol. 24, 2010, p. 289-299.
-
Breiman L. Random forests, machine learning 45. Journal of Clinical Microbiology, Vol. 2, 2001, p. 199-228.
-
Wu Z., Huang N. E. A study of the characteristics of white noise using the empirical mode decomposition method. Proceedings Mathematical Physical and Engineering Sciences, Vol. 460, 2004, p. 1597-1611.
-
Shannon C. E. A mathematical theory of communication. Bell System Technical Journal, Vol. 27, 1948, p. 3-55.
About this article
This research was supported by the National Natural Science Foundation of China (Grant Nos. 61074083, 50705005, and 51105019), and by the Technology Foundation Program of National Defense (Grant No. Z132013B002).
