Hydraulic pump fault diagnosis with compressed signals based on stagewise orthogonal matching pursuit

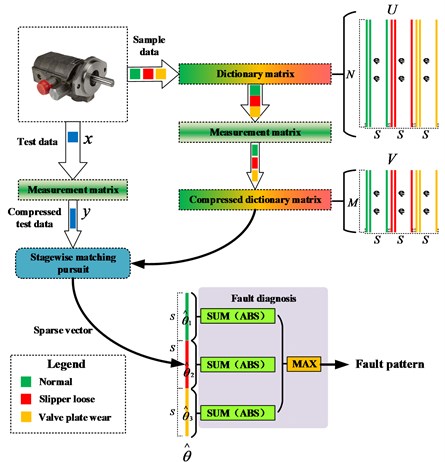
2.1. Vibration data compression

Suppose the length of test vibration data is $N$, and is denoted as $x$. The measurement matrix is $\mathrm{\Phi }$, and its size is $M$×$N$, in this study, Gaussian random matrix is selected as the measurement matrix. Then, the test data is compressed as:

Meanwhile, dictionary matrix is also compressed with measurement matrix $\mathrm{\Phi }$.

Generally speaking, $M$ is much smaller than $N$, and $M/N\le$0.5. In this way, the monitoring data of hydraulic pump is compressed, and the transmission bandwidth consumption is reduced.

2.2. Dictionary matrix construction

The dictionary matrix is composed of sample data acquired from normal working condition, slipper loose fault pattern and valve plate wear fault pattern. For each pattern, suppose the length of signal is $L$, and the sampling frequency is $f_S$, the sampling time is $t$, thus, for each pattern:

Then the sample data are divided into several segments, and the length of each segment is $N$, same with the length of test data, and the number of segments are:

The segments from the same pattern are arranged together as dictionary matrix $U$, therefore, the size of dictionary matrix is $N$×$3S$, as shown in Fig. 1.

After that, the dictionary matrix is also compressed with the measurement matrix, and the size of compressed dictionary matrix is $M$×$3S$:

Later, after compression, these compressed segments are used for compressed test data representation.

2.3. Stagewise orthogonal matching pursuit

The Stagewise Orthogonal Matching Pursuit (StOMP) is proposed by Donoho, in his paper [6], StOMP aims to achieve an approximate solution to $y=V\theta$, where $V$ comes from Uniform Spherical ensemble, and $\theta$ is sparse. However, in our study, the compressed dictionary matrix $V$ plays the role of matrix $V$.

The details of StOMP algorithms used for fault diagnosis are shown in as follow. In the following, $r_t$ is the residue, $t$ is the iteration counter (its max value is $P$), $J_t$ is the index numbers (column ordinals) of each iteration, ${\mathrm{\Lambda }}_t$ is the union set of $t$ times iteration, $v_j$ is the $j$th column of matrix $V$, $V_t$ is the subset of $V$, which is selected according to ${\mathrm{\Lambda }}_t$.

StOMP algorithm procedure:

Input:

• The compressed dictionary matrix $V$, size: $M$×$3S$;

• The compressed test data $y$, size: $M$×$1$, and $y=V\widehat{\theta }$,

• The maximum number of iteration stages $P$,

• The threshold parameter $t_t$.

Output:

• The sparse vector $\widehat{\theta }$;

• The residual $r_p=y-V_p{\widehat{\theta }}_p$, size: $N$×$1$.

Detail procedure step:

(1) Initialization: $r_0=y$, ${\mathrm{\Lambda }}_0=\varnothing$, $V_0=\varnothing$, $t_1=1$.

(2) When it is the $t$th stage.

Calculate current residual $Th$:

here ${\sigma }_t$ is a formal noise level and $t_t$ is a threshold parameter.

Then applies matched filtering to the current residual, getting a vector of residual correlations:

The procedure next performs hard thresholding to find the significant elements (a small set $J_t$ of “large” coordinates):

(3) Updating the estimate, meaning merge the subset of newly selected coordinates with the previous support estimate:

When ${\mathrm{\Lambda }}_t={\mathrm{\Lambda }}_{t-1}$, procedure could be go to Step 4.

(4) Calculate least squares solution of $y=V_t{\theta }_t$:

(5) The updated residual is:

(6) We check a stopping condition ($t+1>P$ or $t_t=0$) and, if it is not yet time to stop, go to the next stage of the procedure.

(7) If it is time to stop, we set $\widehat{\theta }={\theta }_t$ as the final output of the procedure.

Finally, we can get the restructure signal $x$:

2.4. Fault diagnosis

By using StOMP algorithm, the sparse vector $\widehat{\theta }$ is calculated. The size of $\widehat{\theta }$ is $3S$×$1$, as shown in Fig. 1 Each element of the sparse vector corresponds to a column in compressed dictionary matrix $V$. According to sparse representation theory, the sample vectors in matrix $V$, which share the same pattern with the test data, represent the test data better than other vectors, in other words, the corresponding elements in vector $\widehat{\theta }$ are larger than others. Thus, in this study, the absolute value sum of each element in each segment is calculated, and the maximum one corresponds to the pattern, as shown in Fig. 1. The details are:

In Eq. (14), $r_1$ denote working condition, $r_2$ denote slipper loose fault pattern, and $r_3$ denote valve plate wear fault pattern:

Fig. 2Plunger pump rig

3.1. Experiment setup

In this study, a plunger pump were employed to verify the effectiveness of the proposed method, the pump is shown in Fig. 2. Based on the statistics of pump faults, two common faults, slipper loose fault and valve plate wear fault, were introduced into the test rig. Vibration data were acquired by an accelerator, which embedded on the end face of the plunger pump, the rotational speed was 528 r/min, and the sampling rate was 1000 Hz.

3.2. Data compression

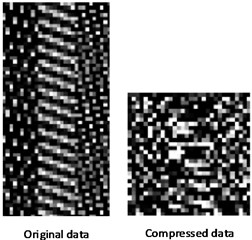
In this paper, size of the measurement matrix was 30×60, as shown in Fig. 1(a), and the figure was based on image gray scale. Fig. 1(b) is the original data and compressed data. With the measurement matrix, the size of the test data was halved. Later, the compressed would be used for fault diagnosis instead of the original data.

3.3. Dictionary matrix construction

The length of an segment (a column in dictionary matrix) is 60, same with the test data, and each pattern contained 20 segments, in other words, here, $N=$60, $S=$60, the size of dictionary matrix was 60×60, as shown in Fig. 3(d). Then, the dictionary matrix was compressed with the measurement matrix, according to Eq. (4), the size of the compressed dictionary matrix is 30×60 (see Fig. 3(b)).

Fig. 3Measurement matrix and data compression

a) Measurement matrix

b) Compressed distionary

c) Data compression

d) Dictionery matrix

3.4. Stagewise orthogonal matching pursuit

Here, the maximum number of iterations $P$ was set as 2. Threshold parameter $t_t$ was set as 0.9, and formal noise level ${\sigma }_t$ was set as ${‖r_t‖}_2/\sqrt{M}$.

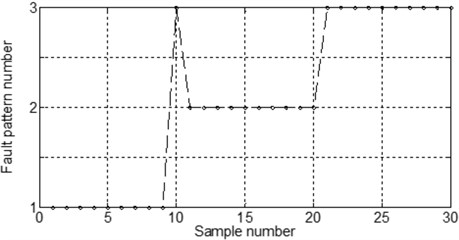
The sparse vector $\widehat{\theta }$, is shown in Fig. 4(a), for test samples No. 1-No. 10, the maximum value area was in the 1st elements to the 10th elements, indicated that the corresponding samples in the compressed dictionary matrix represented the test samples better than others. Other test samples shared the same appearance.

3.5. Fault diagnosis

The results of fault diagnosis is shown in Fig. 4(b). In 30 test samples, only 1 samples were diagnosed incorrectly, thus, the accuracy of the proposed method is 96.67 %. The time consumption is 0.47 seconds.

Fig. 4Sparse vectors and diagnosis results

a) Sparse vectors

b) Diagnosis results

3.6. Time consumption comparison

In this part, the test samples were used for fault diagnosis based on Orthogonal Matching Pursuit (OMP) algorithm, and the total time consumption is 3.25 seconds, and the diagnosis accuracy is 96.25 %. Therefore, fault diagnosis based on StOMP algorithm is faster than OMP algorithm.