Abstract
As the power source of the hydraulic system, the performance of the hydraulic pump is quite crucial for the normal operation of the entire system. The purpose of this study is to propose a method of fault diagnosis for hydraulic pump based on intrinsic time-scale decomposition (ITD) and softmax regression. First, proper rotation components are obtained by processing the pump’s vibration data with ITD, which is an efficient and precise time-frequency-energy analysis method of signals. Then the feature vector which contains state information of present moment is formed by the energy values of the components. Finally, the softmax regression model is trained to classify possible fault modes, and the gradient descent method is applied to determine the parameters of the model. The effectiveness and feasibility of the proposed method have been validated by a case study based on the vibration signals of a real hydraulic pump under different fault modes.
1. Introduction
Hydraulic systems have been widely used in aeronautics, astronautics, automobiles and so on. As the heart of a hydraulic system, hydraulic pump significantly influences the operation of the entire system. Under abnormal states, hydraulic pumps are generally accompanied with vibration change [1, 2]. Thus it is particularly important to realize real-time fault diagnosis of hydraulic pump by using the monitoring signals. This study provides a novel fault diagnosis method for hydraulic pump based on intrinsic time-scale decomposition (ITD) and softmax regression.
In general, the entire fault diagnosis process mainly includes two key procedures: feature extraction and mode classification. For feature extraction, reliable feature representative of the pump condition should be extracted by the analysis of vibration signal measuring on the pump at first. However, the failure mechanism of hydraulic system is so complex that the accurate failure feature is difficult to obtain. So common signal processing methods are not sufficiently applicable for characteristic extraction of a hydraulic pump. The empirical mode decomposition (EMD) has been widely used to process nonlinear and non-stationary signal effectively [3]. But in its application, smoothing out the uneven amplitudes via sifting can prevent faithful extraction of waves. Moreover, repetitive sifting causes smearing of information across different decomposition levels, which is unlikely to reflect the intrinsic characteristics of the signal under analysis. To overcome the limitation of EMD, the ITD method is proposed along with the underlying monotonic signal trend, without the need for laborious and ineffective sifting or splines [4-6]. It can decompose a signal into a sum of proper rotation components and a monotonic trend, which makes it efficient and precise for time-frequency-energy analysis of signals. Instantaneous frequency and amplitude are well defined in the proper rotation components.
As an expansion of logistic regression, softmax regression generalizes logistic regression to the multi-class classification setting, where the classes are mutually exclusive. As a multi-class model, softmax regression is more applicable to multi-class classification problems such as fault diagnosis of hydraulic pump, which need to classify three conditions: the normal state, the slipper loosing fault and the valve plate wear fault. Since all the classes are modeled simultaneously in a unified process, the outputs are directly comparable to arrive at the prediction and the class distribution is relatively more balanced, which makes softmax regression a proper classification algorithm to solve the fault diagnosis problem.
In order to process the nonlinear vibration signals and achieve accurate fault classification of hydraulic pump, an approach based on ITD and softmax regression is proposed. This paper is structured as follows. In Section 2, the fundamental mathematical principles of the ITD and softmax regression are illustrated. Section 3 explains the case study of hydraulic pump fault classification, which is performed to validate the proposed method. Section 4 draws the conclusion.
2. Methodology
2.1. Procedures of the method
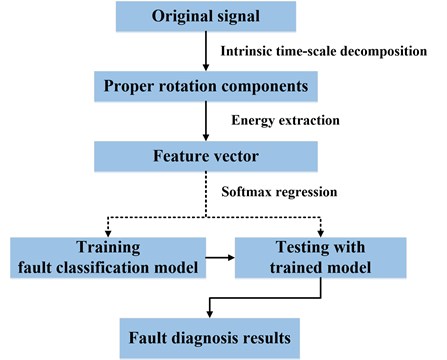
The methodology has two main steps as below:
The first step involves the time-frequency-energy analysis of the vibration signals based on ITD. Proper rotation components are decomposed from original signals and the form of feature vector is based on energy extraction;
In the second step, softmax regression model is employed to realize the fault mode classification. The training dataset of former feature vector is used to train the fault classification model, which is tested by the testing dataset then. The procedure of the methodology can be summarized as Fig. 1.
Fig. 1The procedure of the proposed methodology
2.2. Feature extraction by using intrinsic time-scale decomposition
The ITD method decomposes a vibration signal into several proper rotation components and a trend component. For the signal , is defined as the baseline extraction operator. After extracting a baseline from the signal , the rest of the signal becomes an inherent rotation. The first decomposition of is as follows:
where is the baseline signal and is the proper rotation component.
Decomposition can extract a baseline signal and a proper rotation component, the latter denoting the local relative high frequency of the decomposed signal. Taking the baseline signal as the input signal, the decomposition is continued until a monotone signal is obtained. Using this method, the original signal is decomposed into several proper rotation components of frequency ranges from high to low and a monotone trend component. The whole process can be expressed as:
where is the th layer of the proper rotation and is a monotone trend or an extracted lowest frequency baseline when the decomposition is stopped before the monotone trend is obtained.
The decomposed components from the ITD method have certain physical meanings. They can effectively reflect the characteristics of the original signal and are suitable for analyzing the amplitude and frequency modulation of the signal [5].
At last, proper rotation components ,…, and the trend component are obtained, as follows:
where is the th ITD component and is the trend component.
The ITD method is applied to decompose the original signal into several proper rotation components with intrinsic time scales. Then, the energy values are calculated as features of the components. Each proper rotation component is processed as following:
where is the energy of Each proper rotation component, and then normalized as below:
where is the normalized energy feature vector which contains key information of original signal. The feature value can change when the hydraulic pump works under different conditions, which can reflect the different fault mode of the pump. Thus, the ITD method can be applied to obtain the feature vector effectively.
2.3. Softmax regression method
Softmax regression is an expansion of logistic regression. Different from traditional logistic regression, softmax regression focuses on multi-class classification. It generalizes logistic regression to the multi-class classification setting, where the classes are mutually exclusive. Given an input , softmax regression estimates the probability of the class label y taking on each of the k different possible values with a -dimensional vector generated from the hypothesis function.
For a test input , the probability that for each value of is estimated by softmax regression. Assume the training set and labels , the hypothesis outputs a -dimensional vector (whose elements sum to 1) and also provides k estimated probabilities. The hypothesis takes the form:
Here are the parameters of the model. Normalized by , the hypothesis for are then equaled to one.
The cost function will be as follows:
where is the indicator function so that 1{a true statement} = 1, and 1{a false statement} = 0. Then it is plugged into a gradient descent algorithm and get a minimum which helps to get the final classification results:
Besides, the cost function is modified by adding a weight decay term , which penalizes large values of the parameters since softmax regression has superfluous parameters and is easy to be over parameterized [7-8].
3. Case study
In this experiment, several datasets generated from a plunger pump test-rig were used to validate the effectiveness of the proposed method. And two commonly occurring faults were injected into the test pump: slipper loosing and valve plate wear. The original vibration data of the hydraulic pump were acquired from the end face of the pump with a motor speed of 528 r/min and a sampling rate of 1000 Hz. Under three conditions including the normal state and two fault conditions, 12 groups of data samples were acquired in total and four samples were obtained for each condition.
Fig. 2ITD result of a normal state signal
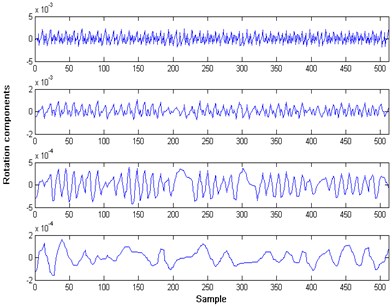
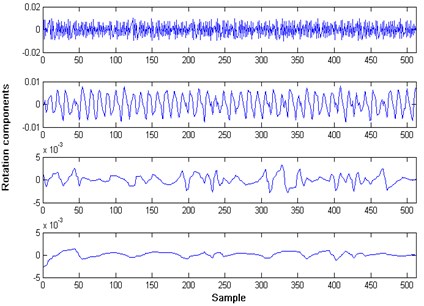
Fig. 3ITD result of slipper loosing condition
3.1. Feature extraction of the vibration signals
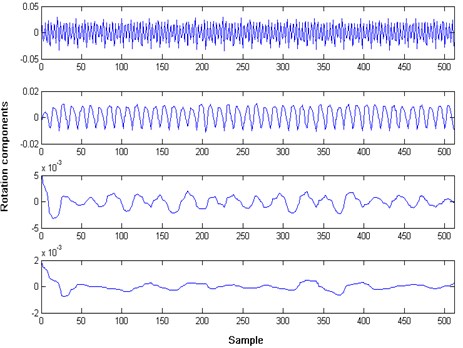
In the process of feature extraction, each raw data was decomposed to acquire the proper rotation components by ITD. Figs. 2-4 shows the results of the intrinsic time-scale decomposition of the normal condition signal and two fault condition signals. Each signal was decomposed into four proper rotation components. Then the normalized energy values of the proper rotation components were extracted to form the feature vector with the assumption that energy of the trend component can be ignored.
Fig. 4ITD result of a valve plate wear signal
3.2. Softmax regression model training for fault classification
In this section, the softmax regression model was applied to recognize the states of the hydraulic pump based on the feature vectors obtained by ITD. For each fault mode, the fault classification model was trained by 250 sets of fault state data versus 250 sets of normal data. And the gradient descent method was employed to determine the parameters of the softmax regression model, which was then used to classify the faults of the hydraulic pump.
The training datasets which contained 40 sets of data under normal condition, 40 sets of data under fault mode 1(slipper loosing), and 40 sets of data under fault mode 2(valve plate wear), were used for validating the trained classification model. The classifying results expressed by the different fault mode probabilities were shown in Fig. 5.
Fig. 5Probabilities of fault modes 1 and 2
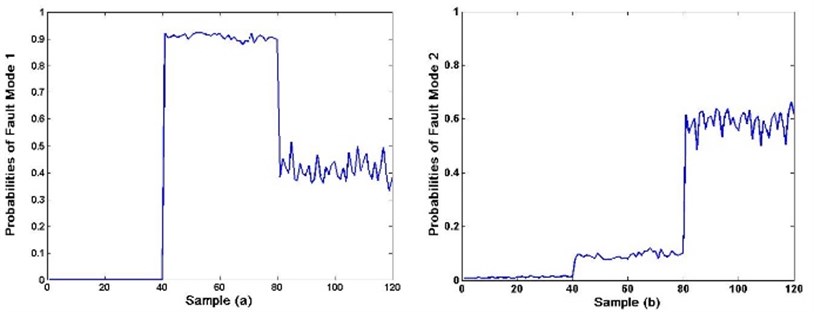
As is shown in Fig. 5, the probabilities of each corresponding fault was much higher than those under other states. For sample (a) in Fig. 5, the probabilities of samples from 41 to 80 was much higher than the samples between 1 and 40 (normal state) together with samples 81 and 120 (fault mode 2), thus drawing the conclusion that the pump was diagnosed with fault mode 1. The result can demonstrate the effectiveness and practicality of fault diagnosis using softmax regression.
4. Conclusions
The fault diagnosis of a hydraulic pump based on ITD and softmax regression was performed in this study. ITD, which is an efficient and precise method for time-frequency-energy signal analysis, can obtain proper rotation components from non-stationary vibration signals. Feature vectors which contain characteristic information are obtained by energy extraction. Finally, as a competitive and efficiency tool for fault diagnosis, softmax regression model are applied to realize dynamic fault classification of hydraulic pump. The proposed method is verified to process non-stationary and nonlinear signals effectively with good diagnosis robustness.
References
-
Mollazade K., Ahmadi H., Omid M., et al. Vibration-based fault diagnosis of hydraulic pump of tractor steering system by using energy technique. Modern Applied Science, Vol. 3, Issue 6, 2009, p. 59-66.
-
Wang J., Hu H. Vibration-based fault diagnosis of pump using fuzzy technique. Measurement, Vol. 39, Issue 2, 2006, p. 176-185.
-
Chen L., Jiameng H., Hongmei L. Application of EMD-AR and MTS for hydraulic pump fault diagnosis. Journal of Vibroengineering, Vol. 15, Issue 2, 2013, p. 761-772.
-
Frei M. G., Osorio I. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, Vol. 463, Issue 2078, 2007, p. 321-342.
-
An X., Jiang D., Chen J., et al. Application of the intrinsic time-scale decomposition method to fault diagnosis of wind turbine bearing. Journal of Vibration and Control, 2011, p. 1077546311403185.
-
Martis R. J., Acharya U. R., Tan J. H., et al. Application of intrinsic time-scale decomposition (ITD) to EEG signals for automated seizure prediction. International Journal of Neural Systems, Vol. 23, Issue 5, 2013, p. 1350023.
-
Ni J. C., Xu Y. L. SAR automatic target recognition based on a visual cortical system. 6th International Congress on Image and Signal Processing (CISP), Vol. 2, 2013, p. 778-782.
-
Zhang X. Y., Wang S., Zhu X., et al. Update vs. upgrade: modeling with indeterminate multi-class active learning. Neurocomputing, Vol. 162, 2015, p. 163-170.
About this article
The authors declare that there is no any potential conflict of interests in the research. This study was supported by the Fundamental Research Funds for the Central Universities (Grant No. YWF-16-BJ-J-18) and the National Natural Science Foundation of China (Grant Nos. 51575021 and 51605014), as well as the Technology Foundation Program of National Defense (Grant No. Z132013B002).
