Fault diagnosis of hydraulic motor based on mathematical morphology filter and sensitive parameters

2.1. Morphological difference operator

Mathematical morphology can filter and demodulate a signal at the same time, thus it can facilitate digital signal processing much more. Erosion, dilation, opening and closing are four basic morphological operators [5-10].

Morphological difference operator and morphological closing operator are adopted in this study, thus they can be defined as follows:

In Eq. (1), morphological difference operator can be got based on dilation and erosion operation of signal $f\left(n\right)$ with structure element $g\left(m\right)$. The operator is made up of Black Top-Hat and White Top-Hat transform. Black Top-Hat transform is good at extracting positive impulsive characteristic information, and White Top-Hat transform is skilled in extracting negative impulsive characteristic information. With being short of prior knowledge, the negative and positive impulsive characteristic information can be extracted at the same time by the operator [10].

In Eq. (2), morphological closing operator, as one part of Eq. (1), can extract positive impulsive characteristic information and depress negative impulsive characteristic information.

2.2. Time domain parameters

Root mean square, skewness, kurtosis, shape factor, impulse factor, clearance factor, kurtosis factor and morphological index are employed to analyze their sensitivities to slipper fault in this study.

When machinery gets fault, amplitudes of a signal are changed, thus probability density function computed based on the amplitudes is also changed.

It can be concluded that the parameters extracted based on the amplitudes can present different change rule and sensitivity degrees. Root mean square indicates energy of a signal, and skewness depicts asymmetric information of amplitude probability density relative to $Y$-axis, and kurtosis describes steep degree of amplitude summit, and kurtosis factor illustrates impulsive feature.

2.3. Morphological index

Patargias firstly proposed concept of morphological index [5].

A fault signal is filtered by morphological closing operator, and $f_1\left(n\right)$ can be obtained. Based on local maximum algorithm, impulse amplitude series $p\left(m\right)$ can be acquired from $f_1\left(n\right)$, and the impulse amplitude at time instants $i$ satisfy:

where $tr$ is threshold and set as 0.35 in this study, goal of the threshold is to weaken influence of noises.

Morphological index is given by following formula:

where $M$ is number of impulses.

Basically, morphological index is transformation of root mean square, because it is also computed based on fault impulsive amplitude. Differences between the two parameters are that morphological index is less influenced by noises than root mean square, and it also indicates much more energy of fault impulse can be extracted.

2.4. Frequency domain parameters

Centroid frequency, mean square frequency and frequency variance are adopted to analyze their sensitivities to slipper fault in this investigation.

Power spectrum of a signal indicates amplitudes and components of frequencies. When machinery becomes fault, the amplitudes and components of a fault signal are changed, and the three parameters are all computed based on amplitudes and components of frequencies, thus their values are also different from normal ones in some degree, and they can present different change regulations and sensitive degrees.

3.1. Extraction of time domain parameters

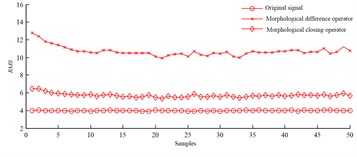
Time domain parameters are extracted from abnormal and normal signals based on morphological difference operator and morphological closing operator, and Fig. 1 displays sensitive distribution of 50 samples of each parameter.

Fig. 1Sensitive distribution of time domain parameters.

a) Root mean square

b) Skewness

c) Kurtosis

d) Shape factor

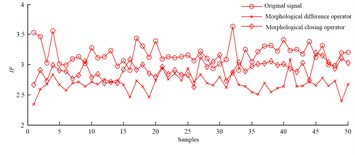
e) Impulse factor

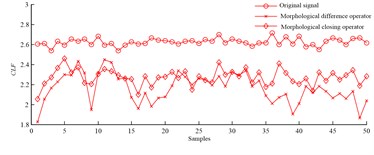
f) Clearance factor

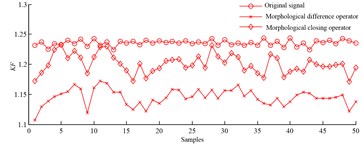
g) Kurtosis factor

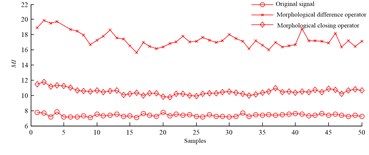
h) Morphological index

Slipper fault signals are filtered by morphological difference operator and morphological closing operator respectively, and root mean square, skew, kurtosis and morphological index are taken from filtered signals. It is can be found from Fig. 1 that the parameter values extracted from fault signals based on the two operators don’t overlap with each other, and the parameter values also don’t overlap with those of normal signals. It should be pointed out that parameter values extracted based on morphological difference operator are much bigger than those obtained based on morphological closing operator, and value of morphological index firstly introduced into hydraulic motor fault field is bigger than that of root mean square. The conclusion is that the four parameters are all sensitive to slipper fault, thus root mean square, skew, kurtosis and morphological index can all be applied to diagnose slipper fault, and morphological index is more sensitive than root mean square.

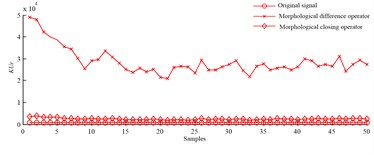
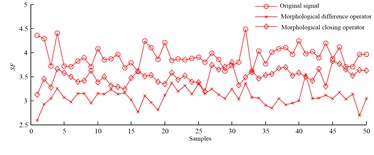
Based on morphological difference operator, shape factor, impulse factor, clearance factor and kurtosis factor are extracted from abnormal signals, and their values don’t overlap with those extracted from normal signals. Conclusions drawn from above demonstrate that these parameters are sensitive to slipper fault, and they can diagnose slipper fault effectively.

Based on method of morphological difference operator, shape factor, impulse factor, and kurtosis factor can be obtained from abnormal signals, and their values overlap with those extracted from normal signals in some degree. Conclusions are summarized from above and show that these parameters are not so much sensitive to slipper fault, and slipper fault can’t be diagnosed effectively.

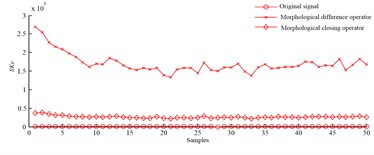
Clearance factor are extracted from abnormal and normal signals based on morphological difference operator and morphological closing operator, and abnormal and normal values don’t overlap with each other, and the parameter is sensitive to slipper fault. What need to be explained are differences between abnormal values and normal ones extracted based on morphological difference operator are bigger than those extracted based on morphological closing operator. Thus, the fault can be diagnosed by the parameter.

Value differences between normal and abnormal parameter extracted based on morphological difference operator is shorted for A, and value differences between normal and abnormal parameter extracted based on morphological closing operator is shorted for B, and A is bigger than B in some degree. Thus, morphological difference operator is prior to morphological closing operator in time domain.

3.2. Extraction of frequency domain parameters

Frequency domain parameters are extracted from abnormal and normal signals based on morphological difference operator and morphological closing operator, and Fig. 1 displays sensitive distribution of 50 samples of each parameter.

Centroid frequency and mean square frequency are extracted from abnormal signals based on both operators, and it can be known from Fig. 2 that their values don’t overlap those extracted from normal signals. The both parameters are sensitive to slipper fault, and the fault can be diagnosed by the two parameters.

Frequency variance is extracted from abnormal signals based on morphological difference operator, and their values don’t overlap with those obtained from normal signals, and therefore the parameter is sensitive to the fault and can diagnose it.

Frequency variance is extracted from abnormal signals based on morphological closing operator, and their values overlap with those got from normal signals in some degree, so the parameter isn’t sensitive to the fault and can’t diagnose it.

Based on morphological closing operator, only frequency variance values extracted from abnormal signals overlap with those extracted from normal signals. And the three parameters extracted based on morphological difference operator all work for the fault diagnosis. Thus, morphological difference operator outperforms morphological closing operator.

Fig. 2Sensitive distribution of frequency domain parameters

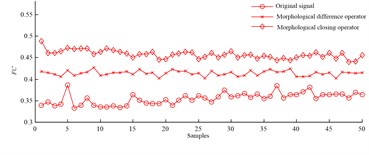
a) Centroid frequency

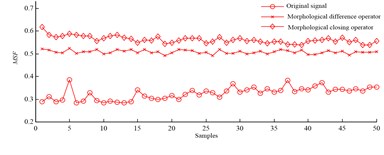
b) Mean square frequency

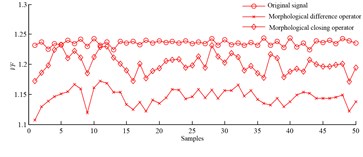
c) Frequency variance