Abstract
The hydraulic pump is the core part of the hydraulic system and impacts the performance of hydraulic directly, thus the diagnosis for hydraulic is crucial. To realize the diagnosis for hydraulic pump, a method utilizing the vibration signal which varies with the performance is proposed. First, ensemble empirical mode decomposition (EEMD) is used to decompose the original signal into finite intrinsic mode functions (IMFs), and then the energy values are extracted to form the feature vector. Second, local tangent space alignment (LTSA), a manifold learning method, is applied in dimension reduction. Third, probabilistic neural network (PNN) is employed as the classifier to recognize the fault pattern. Finally, the effectiveness of the proposed method is validated by the experimental data with different faults.
1. Introduction
Hydraulic system is widely used in aeronautics, astronautics, watercraft, weaponry and other large scale engineering. As the critical part of hydraulic system, the hydraulic pump provides the hydraulic energy for the system. Once the fault occurred in hydraulic pump, it would directly result in the performance degradation of hydraulic system and even the entire system [1]. Therefore, the fault diagnosis for hydraulic pump is absolutely essential.
The vibration signal of hydraulic pump changes with the degradation of its performance. A proper and reliable feature can be extracted from vibration signal to indicate its performance [2]. However, the working environment of hydraulic pump is varied and the failure mechanism is complex. The vibration signal is nonlinear and non-stationary, and generally hidden in the noise signal. Therefore, it is difficult to obtain a proper and reliable feature by using common method efficiently.
Empirical mode decomposition (EMD) is development and demonstrated to be superior to common methods, such as wavelet transformation. Based on the assumption that any signal consists of different simple intrinsic mode of oscillations, any complicated signal can be decomposed into finite intrinsic mode functions (IMFs). However, the major drawback of EMD caused by signal intermittency is the mode mixing, which is IMF either consisting of signals with disparate scales or a similar scale existing in different IMFs. To improve the original EMD, the ensemble empirical mode decomposition (EEMD) is proposed with noise assisted data analysis [3], utilizing added white noise to remove the influence of mode mixing.
High-dimensional feature vectors extracted by EEMD lead to high time and space consumption. To improve efficiency of diagnosis, the feature vectors are reduced by some dimension reduction methods generally. Considering the simple algorithmic implementation, strong robustness and the global optimization, the local tangent space alignment (LTSA), a kind of manifold learning method, is employed in dimension reduction, which meets the nonlinear requirement in hydraulic pump [4].
A proper classifier also has a better effect on the diagnosis. Due to the capability to nonlinear problems, fast training and high stability, probabilistic neural network (PNN) is applied as classifier for fault classification in this paper [5].
The organization of this paper is explained as follows: in Section 2, the proposed method based on EEMD-LTSA and PNN is introduced in details; in Section 3, a case study is performed and the method is validated by experimental data; in Section 4, the conclusion is summarized and the future research direction is given.
2. Methodology
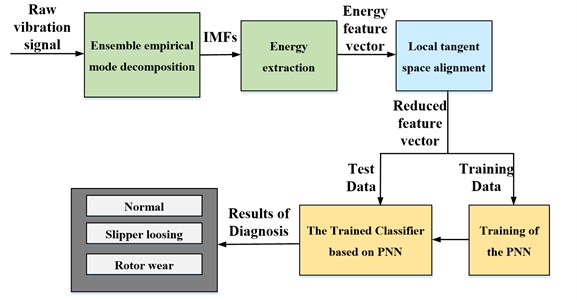
The fault diagnosis for hydraulic pump has three major steps:
1) The EEMD is employed to decompose the original signal. Then the feature vector is obtained by energy extraction.
2) The dimension reduction of energy feature vector is realized by LTSA;
3) PNN is trained by the training data of reduced feature vector, and the trained PNN is serve as the classifier.
Fig. 1 shows the schematic diagram of fault diagnosis proposed in this paper.
Fig. 1Schematic diagram of fault diagnosis proposed
2.1. Feature extraction using EEMD
EEMD improved the original EMD by using noise assisted data analysis. By employing adding Gaussian random white noise with uniform distribution and constant standard deviation of amplitude, EEMD decomposition does avoid the mode mixing [6]. In order to eliminate the effect of the Gaussian white noise, the ensemble average of each IMFs is calculated. The ensemble mean is considered as the true IMFs, since the statistical mean of uncorrelated random sequence is zero,
The process of EEMD is described as follows:
(1) Add a random white noise signal to the original signal , and obtain the noise-added signal :
where is the th implementation of EMD, 1, 2, 3,..., and is the total number of implementation of EMD
(2) Decompose the into finite number of IMFs and residue by using EMD:
where is number of IMFs, and 1, 2, 3,..., .
(3) Procced step (1) and step (2) for times;
(4) Calculate the ensemble means of each corresponding IMF:
(5) Output the as the IMFs obtained from EEMD.
After the ensemble empirical mode decomposition, features are extracted from the each IMFs by energy extraction. Different resonance frequency components appear in the vibration signal when different fault occurred in the hydraulic pump. And the energy of signal varies according to the frequency distribution in each IMF. Therefore, the energy value can reflect the performance degradation of the hydraulic pump. Suppose the energy of residue signal can be ignored, energy of each IMFs defined as follows:
Normalized as below:
where is a vector as the fault feature.
2.2. Dimension reduction by LTSA
LTSA has demonstrated an optimized function to find meaningful low-dimensional structures hidden in high-dimensional sample data. The key technologies of LTSA algorithm is to construct local tangent spaces with local geometry information and align the local tangent spaces to obtain the global coordinate system [7]. The LTSA algorithm is detailed as follows:
(1) Defined the original signal as , which is a data set of points in . Compute the -nearest neighbors of each sample, and the neighborhood matrix is:
where the is the distance between and .
(2) The centered matrix is , where the and is a -dimensional vector of all 1’s. Then singular value decomposition of is performed:
where is the left singular vector of .
The projection coordinates of in the tangent space is:
(3) Align the local coordinates , 1, 2,…, to generate the global coordinate, defined as:
Minimize the global reconstruction error to obtain the global embedding result:
2.3. Fault diagnosis based on PNN
PNN is a neural network based on Bayesian decision theory with a wide range of applications in classification. The training of PNN is concise and fast and the ability of classification is strong [8]. Therefore, PNN is employed for fault diagnosis in this paper.
The structure of PNN is shown in Fig. 2. PNN is a feedforward neural network with four layers: input layer, model layer, summation layer and decision layer.
The input layer contains units that are merely distributed units, which have functions to transfer the sample data to each unit in modern layer.
Fig. 2General configuration of PNN
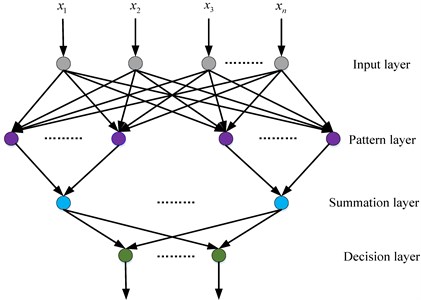
The modern layer is regarded as the cluster center. In this layer, the number of nodes with specific exponential function are equal to the number of patterns of all training samples.
The summation layer is designed to sum up input from modern layer and compute the probability.
In the output layer, units produce binary outputs. The output of maximum probability is 1, correspond to the sample category, while others outputs are 0 [9].
In the process of diagnosis, the training samples are used to train the PNN neural network and the input and output weight as well as other parameters are determined in the learning stage. In recalling stage, the trained PNN neural network is applied to recognize the system pattern.
3. Experimental results
To demonstrate the proposed method, two commonly faults, including slipper loosing and rotor wear, were injected to an experimental hydraulic pump.
By using the accelerate transducer, several groups of vibration signal comprised with normal data, slipper loosing data and rotor wear data, were generated from the end face of the test hydraulic system. The motor speed was 528 r/min and the sampling rate was 1000 Hz. 110 sets of normal date, 110 sets of slipper loosing fault data and 110 sets of rotor wear data were acquired from the experimental equipment.
First, each original vibration signal was decomposed into 8 IMFs and a residue signal by EEMD. Fig. 3 shows a sample result of the decomposition. Then the energy values were extracted from each IMF as the initial eigenvector. Each eigenvector has 8 eigenvalues with the assumption that energy of residue signal can be ignored.
Second, LTSA is applied to reduce the dimensionality of the initial energy eigenvector. Through this process, each initial energy eigenvector was converted to a new eigenvector with 3 characteristics.
After the original data were processed by EEMD and LTSA, for each status, 110 eigenvectors were acquired, and totally 330 eigenvectors were acquired.
To train the PNN, 300 eigenvectors were selected as the training data, and their labels were set as shown in Table 1. The function spread of PNN was set to 0.29.
Table 1Training eigenvectors for fault diagnosis
Pattern | Sample size | Label data |
Normal | 100 eigenvectors | 1 |
Slipper loosing | 100 eigenvectors | 2 |
Rotor wear | 100 eigenvectors | 3 |
Fig. 3A sample of decomposition result of EEMD
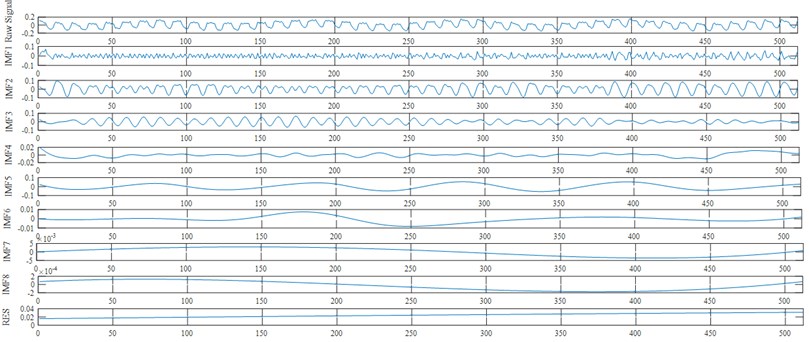
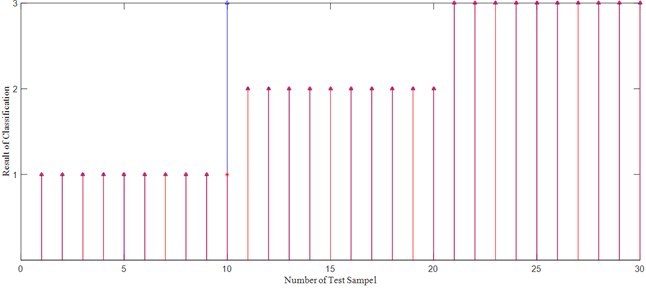
Fig. 4The results of diagnosis
After the training of PNN, the other 30 eigenvectors as the test data were sent to the trained classifier based on PNN.
The results of fault diagnosis are shown in Fig. 4, in which the actual labels of testing sample are marked with red point, while the predicted labels are marked with blue point. No. 1 to No. 10 are the normal data. No. 11 to No. 20 are the slipper loosing fault data. No. 21 to No. 30 are the rotor wear fault data. In the test of normal data, the classification result of 1 test sample didn’t match the actual label. In the test of slipper loosing fault data, all of the classification results were correctly corresponding to the actual fault. In the test of rotor fault data, all of the classification results were correctly corresponding to the actual fault.
In total, 1 test sample is incorrectly judged in the 30 samples, and the corresponding diagnosis accuracy was 96.67 %.
4. Conclusions
This paper presents a novel fault diagnosis approach for hydraulic pump. Original vibration signal is decomposed into finite IMFs, from which energy values are extracted. Then the LAST is employed to reduce dimension of initial feature vectors to 3 dimensionalities. After training the PNN neural network, diagnosis is realized by trained PNN neural network as a classifier. The experimental results indicate that the proposed diagnosis method can diagnose faults effectively and reach a high accuracy.
The proposed approach could be further improved by testing with more data from other fault modes or other hydraulic pump test rig to make it more applicable to fault diagnosis for hydraulic pump.
References
-
Lu C., Ma N., Wang Z. Fault detection for hydraulic pump based on chaotic parallel RBF network. EURASIP Journal on Advances in Signal Processing, Vol. 49, 2011, p. 1-10.
-
Mollazade K., Ahmadi H., Omid M., Alimardan R. An intelligent combined method based on power spectral density, decision trees and fuzzy logic for hydraulic pumps fault diagnosis. International Journal of Intelligent Systems Technologies and Applications, Vol. 3, Issue 8, 2008, p. 551-563.
-
Wu Zhaohua, Huang Norden E. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis, Vol. 1, Issue 1, 2011, p. 1-41.
-
Zhang Z., Zha H. Principle manifolds and nonlinear dimensionality reduction via tangent space alignment. SIAM Journal of Scientific Computing, Vol. 26, Issue 4, 2003, p. 313-338.
-
Sun Zhi-hong, Duan Hong-mei, Hao Jian zhong Fault diagnosis of diesel engine cylinder wall based on Matlab probabilistic neural network. International Conference on Computational Problem-Solving, 2012, p. 465-468.
-
Lei Y., He Z., Zi Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing, Vol. 23, Issue 4, 2009, p. 1327-1338.
-
Wang J., Jiang W., Gou J. Letters: Extended local tangent space alignment for classification. Neurocomputing, Vol. 77, Issue 1, 2012, p. 261-266.
-
Mo F., Kinsner W. Probabilistic neural networks for power line fault classification. IEEE Canadian Conference on Electrical and Computer Engineering, 1998, p. 585-588.
-
Chen X., Zhou J., Xiao J., Zhang X., Xiao H., Zhu W., Fu W. Fault diagnosis based on dependent feature vector and probability neural network for rolling element bearings. Applied Mathematics and Computation, Vol. 247, 2014, p. 835-847.
About this article
This study was supported by the Fundamental Research Funds for the Central Universities (Grant No. YWF-16-BJ-J-18) and the National Natural Science Foundation of China (Grant Nos. 51575021 and 51605014), as well as the Technology Foundation Program of National Defense (Grant No. Z132013B002).
