Rolling bearing fault diagnosis using improved LCD-TEO and softmax classifier

2.1. An improved LCD method

In this paper, slope-based method (SBM) is used to restrain end effect while noise-assisted analysis approach is applied to weaken mode mixing in the process of LCD.

For the signal $x\left(t\right)$ depicted in Fig. 1(a), let ($u\left(i\right)$, $U\left(i\right)$) and ($v\left(i\right)$, $V\left(i\right)$) be the coordinates of the $i$th maximum $\mathrm{M}\mathrm{a}\mathrm{x}\left(i\right)$ and the $i$th minimum $\mathrm{M}\mathrm{i}\mathrm{n}\left(i\right)$. Fig. 1(b) considers the case when a maximum is the first extremum in the front of a signal. Then slope $s_1$ and slope $s_2$ are defined as:

Then, the time gaps between the first two successive maxima and minima are determined as $\mathrm{\Delta }{t}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(1\right)=u\left(2\right)-u\left(1\right)$ and $\mathrm{\Delta }{t}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(1\right)=v\left(2\right)-v\left(1\right)$. The new boundary extrema $\mathrm{M}\mathrm{i}\mathrm{n}\left(0\right)$ and $\mathrm{M}\mathrm{a}\mathrm{x}\left(0\right)$ are newly defined and shifted according to the corresponding time gaps $\mathrm{\Delta }{t}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(1\right)$ and $\mathrm{\Delta }{t}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(1\right)$, and gradients $s_1$ and $s_2$. The coordinates of new extrema are located at:

Fig. 1a) The time series x(t); b) the illustration of the slope-based method

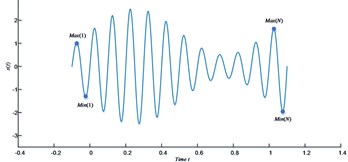
a)

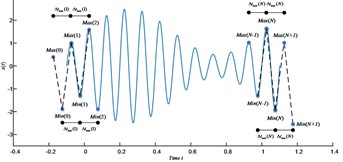
b)

Here, we used LCD to analyze a simulated signal:

The result of LCD to $x\left(t\right)$ using SBM and mirror method (MM) is shown in Fig. 2, from which we can see that LCD with SBM can decompose this signal more efficiently and accurately into a set of ISC_s than with MM.

To restrain mode mixing, white noises are added to homogenize the scale in time-frequency space. To improve the decomposition performance of LCD, the ideas of EEMD are learnt and referred to in this study.

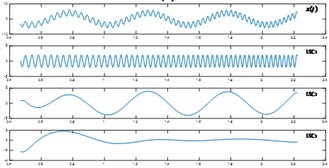
To verify the validity of this method, we analyzed a simulated signal $y\left(t\right)=\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi 80t\right)+y_2\left(t\right)$ shown in Fig. 3(a). Here, $y_2\left(t\right)$ is a high-frequency intermittent signal with amplitude 0.1 and frequency 1600 Hz riding on the third peak of the sinusoidal signal. According to Fig. 3(b), the first $ISC1\left(t\right)$ is the mixture of both low-frequency sinusoidal and high-frequency intermittent signal, which means mode mixing occurs. Fig. 3(c) shows the noises assisted LCD can decompose the original signal more effectively ($Ne=$ 100).

Fig. 2a) The signal x(t); b) The result of LCD using MM; c) The result of LCD using SBM

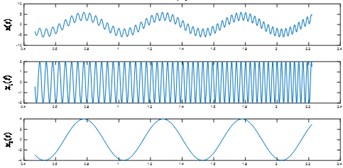
a)

b)

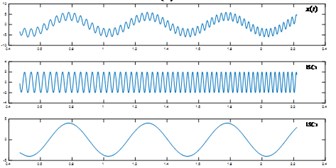
c)

Fig. 3a) The signal y(t); b) The result by original LCD; c) The result with added noises

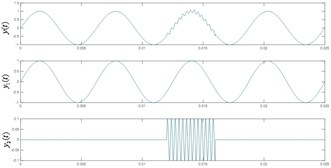
a)

b)

c)

2.2. Fault diagnosis scheme based on improved LCD, TEO and softmax classifier

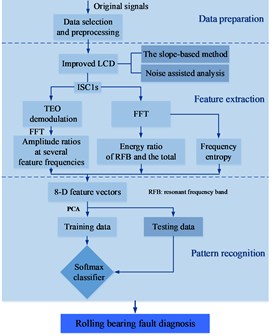
In this part, a new fault diagnosis approach based on improved LCD, TEO demodulation and softmax classifier is proposed. The scheme of fault identification is depicted in Fig. 4. The main steps are described briefly below:

(1) Decompose preprocessed signals into several ISC_s using improved LCD method.

(2) Obtain IA of ISC_1s by calculating TEO, then extract frequency spectra of IA of ISC_1s by FFT.

(3) Compute amplitude ratios at the inner race, outer race and ball fault frequency and their second harmonic frequency in the frequency spectrum of demodulated ISC_1s, and apply FFT to obtain frequency spectra of ISC_1s, calculate its frequency entropy (FE) and energy ratios of resonant frequency band (RFB) against the total. Then, an 8-Dimension feature vector is obtained.

(4) Use PCA for dimensionality reduction.

(5) Train softmax classifier using train data and identify fault modes of test data.

Fig. 4Flowchart of fault diagnosis

3.1. Data preparation

All vibration data are from Bearing Data Center of Case Western Reserve University. The drive end accelerometer data under the normal, inner race fault, outer race fault located at 6 o’clock and ball fault with fault diameters of 7 mils are selected and each datum is divided into 20 segments, and each segment has 6000 points.

3.2. Features extraction based on improved LCD-TEO and FE

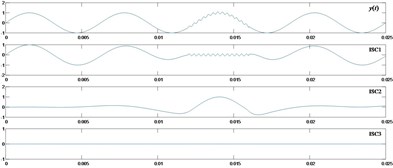
The original signals are decomposed into ISC_s firstly. The ISC₁ is extracted for the first few ISC_s always contain the majority of fault information. Fig. 5 depicts the spectra of demodulated ISC_1s. The three fault feature frequencies of inner race, outer race and ball fault are worked out. Next, several amplitude ratios mentioned above are computed.

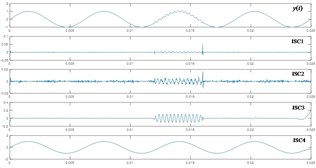
However, the identification performance only using feature variables comprised of amplitude ratios at several feature frequencies is just moderate, especially for the ball fault. The spectra of ISC_1s are shown in Fig. 6, and two new feature variables, energy ratio of resonant frequency band against the total and frequency entropy are added into the feature vector. At last, a complete 8-D feature vectors, are extracted as intrinsic information of bearing fault. Here, the basic principle of entropy is briefly introduced. Entropy is defined to measure complexity and self-similarity of the series, and can reflect complexity changes of intrinsic oscillation.

3.3. Feature reduction using PCA

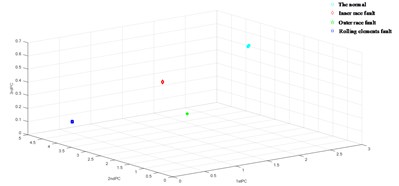
For a diagnosis model, the huge amount of features will probably decrease the robustness, and even cause a decline in the diagnostic accuracy. Therefore, high dimensional features are projected into a three-dimensional space by PCA.

With feature visualization, we analyzed these obtained features. As shown in Fig. 7, the extracted feature vectors by the improved LCD method has good clustering results, therefore this method has high robustness and diagnosis accuracy.

Fig. 5Spectra of IA of ISC1s

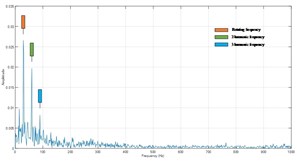
a) The normal

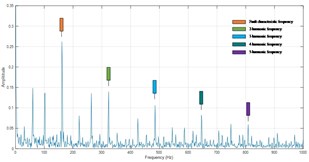
b) Inner race fault

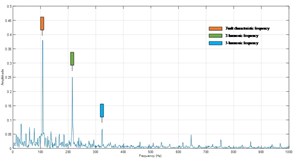
c) Outer race fault

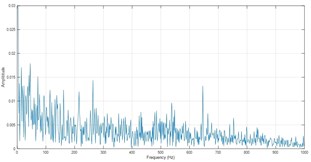
d) Ball fault

Fig. 6Frequency spectra of ISC1s

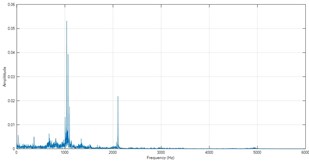
a) The normal

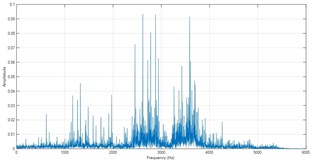
b) Inner race fault

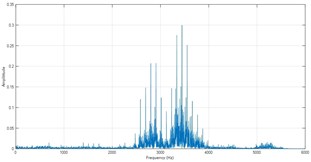
c) Outer race fault

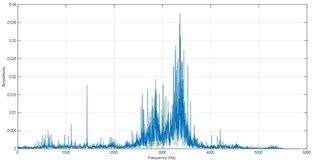
d) Ball fault

Fig. 7Features clustering chart with improved LCD

3.4. Pattern recognition using softmax classifier

3-Dimension fault feature vectors of bearings are obtained by feature extraction and dimension reduction method. Softmax classifier is employed to recognize automatically faults. Identification results are listed partly in Table 1.

The proposed approach can identify effectively fault patterns of bearing and has the high accuracy.