Study of the influence of the resonance changer on the longitudinal vibration of marine propulsion shafting system

Li, Zhengmin; He, Lin; Cui, Hanguo; He, Jiangyang; Xu, Wei

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

Study of the influence of the resonance changer on the longitudinal vibration of marine propulsion shafting system

Zhengmin Li¹

Lin He²

Hanguo Cui³

Jiangyang He⁴

Wei Xu⁵

^{1, 2, 4, 5}Institute of Noise and Vibration, Naval University of Engineering, Wuhan, China

^{1, 2, 4, 5}National Key Laboratory on Ship Vibration and Noise, Wuhan, China

^{3, 1}Department of Mechanical Engineering, College of Power Engineering, Naval University of Engineering, Wuhan, China

Corresponding Author:

Wei Xu

Cite the article Download PDF

Downloads 1345

Abstract

For investigating the characteristics of the resonance changer and its influence on the longitudinal vibration of marine propulsion shafting system, by the transfer matrix method, the model of the shafting system, including the resonance changer is established. The influences of the resonance changer with various designing parameters on the force transmissibility through the thrust bearing foundation are evaluated. The results show that, the introduction of the resonance changer eliminates the resonance at original 1st natural frequency and introduces another two resonance peaks, as well as significantly lowering the maximum response compared with the original peak. The right one is attributed to the resonance changer, while the other is due to excitation of the other shafting system components. The 2nd natural frequency moves towards the high frequency direction and the peak value nearly stay invariable. If the designing parameters of the resonance changer are well optimized, the objective of reducing the longitudinal vibration transmission through the shafting system to the hull could be achieved.

1. Introduction

For marine vessels, when the blade passing frequency of the propeller is equal or close to the natural frequency of the shaft longitudinal vibration, there will be excessive longitudinal vibration of the shafting system, which is not only the reason of the fatigue damage of the shaft and the wear of the thrust bearings, but also the main source for low frequency shipboard noise and underwater sound radiation from a submarine hull. For reducing the propeller-induced longitudinal vibration, several methods are presented [1-4], i.e. increasing the number of propeller blades, moving the thrust bearing further afterward, and adopting new thrusters such as water jet propulsion device. Such method is difficult to implement and is not always effective. The resonance changer (also called RC) [4] proposed by GOODWIN is a new option in reducing the propeller-induced vibration, and since then it has received much more attentions.

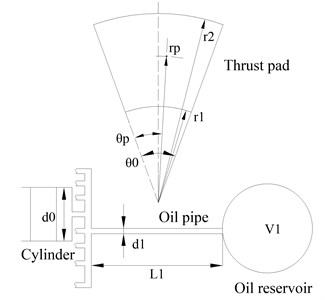
Fig. 1 shows a thrust bearing which is a combination of a fluid-equalized thrust bearing [5] and a RC, and it could help reduce shaft longitudinal vibration. The thrust pads are supported by pistons which are in turn supported by hydraulic fluids. The piston cylinders are all interconnected and the supported fluids are connected to an oil reservoir through an oil pipe. The axial load is carried by the supported fluids and the disturbance forces are transmitted to the oil reservoir through the oscillatory oil pressure in the oil pipe. In this procedure, the virtual stiffness $K_{h}$ is produced by the compression and expansion of the oil in the reservoir, and the virtual mass $M_{h}$ and virtual damping $C_{h}$ are produced by the viscous oil flow in the oil pipe. So, the piston cylinders, the supported fluids, the oil pipe as well as the oil reservoir work together as a RC. A replenishment hydraulic fluid system is also provided to compensate for shaft movement due to fluid leakage and the compression or expansion of the oil in the reservoir. Fig. 2 shows the main designing parameters of a thrust bearing with a RC, including $r_{1}$ , $r_{2}$ , $θ$ , $r_{p}$ , $θ_{p}$ , $m$ , $V_{1}$ , $d_{0}$ , $L_{1}$ , $d_{1}$ , which represent the inner radius of pad, the outer radius of pad, the angular of pad, the radius of supported point, the angular of the supported point, the number of thrust pads and oil cylinders, the volume of the oil reservoir, the diameter of the piston cylinder, the length and diameter of the oil pipe, respectively.

Fig. 1A schematic diagram of a thrust bearing with a RC

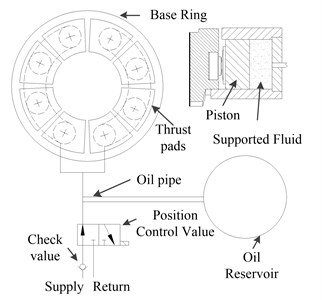
Fig. 2Specifications of a thrust bearing with a RC

2. Model of longitudinal vibration of propulsion shafting system

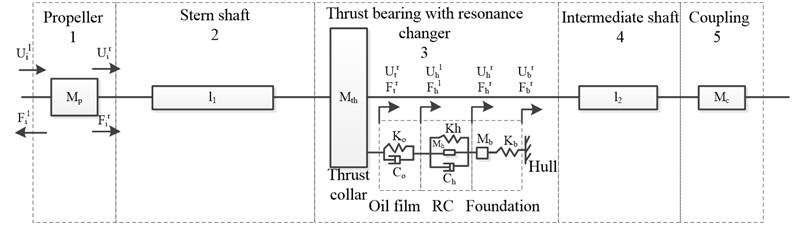
The main propulsion shafting system of a marine vessel can be simplified into the key features shown in Fig. 3 as far as the axial vibration is concerned, where $U_{i}^{l}$ , $F_{i}^{l}$ , $U_{i}^{r}$ , $F_{i}^{r}$ represent the amplitude of displacement and force of component $i$ , and superscripts ‘ $r$ ’ and ‘ $l$ ’ denote the right end and the left end of component $i$ . Subscript ‘ $i$ ’ denotes different component. In detail, ‘1’,‘2’,‘3’,‘4’,‘5’ denote the propeller, the stern shaft, the thrust bearing, the intermediate shaft and the coupling, respectively, and ‘ $t$ ’, ‘ $h$ , ‘ $b$ ’ denote the thrust collar, the RC, the foundation, respectively. $T_{i}$ represents the transfer matrix of component $i$ .

Fig. 3A model of longitudinal vibration of propulsion shafting system

2.1. Model of the thrust bearing with a resonance changer

The simplified model of the RC is shown in Fig. 3. As described in literature [4], a mathematical analysis can be made as followings:

1

{F_{h}^{l} = A}_{0} P = \frac{ρ_{1} L_{1} A_{0}^{2}}{A_{1}} ({\ddot{U}}_{h}^{r} - {\ddot{U}}_{h}^{l}) + 8 π μ_{1} L_{1} \frac{A_{0}^{2}}{A_{1}^{2}} ({\dot{U}}_{h}^{r} - {\dot{U}}_{h}^{l}) + \frac{A_{0}^{2} B_{1}}{V_{1}} (U_{h}^{r} - U_{h}^{l}),

where, $A_{0} = m π {(d_{0}^{2} / 2)}^{2}$ is the total cross-sectional area of the supported fluids, $A_{1} = π {(d_{1}^{2} / 2)}^{2}$ is the cross-sectional area of the oil pipe, and $P$ , $ρ_{1}$ , $μ_{1}$ , $B_{1}$ are the oil pressure in the piston cylinder, the density of the oil, the oil viscous and the bulk modulus of the oil, respectively. Then, $M_{h}$ , $K_{h}$ , $C_{h}$ , and $F_{h}$ can be given by Eq. (2). $F_{h}$ is the natural frequency of the RC. The transmission matrix of the RC is respectively expressed as Eq. (3), in which $ω$ is the angular frequency of the disturbance forces:

2

M_{h} = \frac{ρ_{1} L_{1} A_{0}^{2}}{A_{1}}, K_{h} = \frac{A_{0}^{2} B_{1}}{V_{1}}, C_{h} = 8 π μ_{1} L_{1} \frac{A_{0}^{2}}{A_{1}^{2}}, F_{h} = \sqrt{\frac{{(B}_{1} A_{1})}{(ρ_{1} L_{1} V_{1})}},

3

T_{h} = [\begin{matrix} 1 & \frac{1}{- M_{h} ω^{2} + K_{h} + j ω C_{h}} \\ 0 & 1 \end{matrix}] .

The transmission matrix of the thrust bearing with a RC and its foundation is shown as:

4

\{\begin{matrix} U_{b}^{r} \\ F_{b}^{r} \end{matrix}\} = [\begin{matrix} 1 & \frac{1}{K_{b}} \\ 0 & 1 \end{matrix}] [\begin{matrix} 1 & 0 \\ - M_{b} ω^{2} & 1 \end{matrix}] [\begin{matrix} 1 & \frac{1}{- M_{h} ω^{2} + K_{h} + j ω C_{h}} \\ 0 & 1 \end{matrix}] [\begin{matrix} 1 & \frac{1}{K_{o} + j ω C_{o}} \\ 0 & 1 \end{matrix}] \{\begin{matrix} U_{t}^{r} \\ F_{t}^{r} \end{matrix}\},

where, $K_{b}$ , $M_{b}$ are the stiffness and mass of the thrust bearing foundation(including the supporting and surrounding structures), and $K_{o}$ , $C_{o}$ are the axial stiffness and damping of the lubricated oil film. The procedure of calculating the dynamic coefficients described in literature [6], which is based on the thermal hydrodynamic lubrication theory and the perturbation equations formulated from a first order Taylor expansion of the oil film and pressure, is adopted in this paper. The hull of the ship or submarine could be regard as a rigid boundary condition, which means $U_{t}^{r} = 0$ . Then, Eq. (4) can be deduced as:

5

{F_{t}}^{r} = K_{e} {U_{t}}^{r}

= \frac{(K_{b} - M_{b} ω^{2}) (K_{o} + j ω C_{o}) (- M_{h} ω^{2} + K_{h} + j ω C_{h})}{(K_{b} - M_{z} ω^{2} + K_{o} + j ω C_{o}) (- M_{h} ω^{2} + K_{h} + j ω C_{h}) + (K_{b} - M_{z} ω^{2}) (K_{o} + j ω C_{o})} {U_{t}}^{r},

where $K_{e}$ represents the equivalent stiffness. $M$ th is the mass of the thrust collar. Then, the transfer matrix of the thrust bearing with a RC and the foundation can be expressed as:

6

T_{3} = [\begin{matrix} 1 & 0 \\ - M_{t h} ω^{2} + K_{e} & 1 \end{matrix}] .

2.2. Model of longitudinal shaft vibration and responds calculation

The transfer matrix of the shafting system $T$ is shown as Eq. (7), in which, $T_{11}$ , $T_{12}$ , $T_{21}$ , $T_{22}$ are the elements of $T$ . The transfer matrices of the propeller and the coupling are expressed as Eq. (5) and the transfer matrix of the uniform shaft undergoing longitudinal vibration is expressed as Eq. (6).Where, $M_{p}$ , $M_{c}$ , $l$ , $E$ , $ρ_{s}$ , $A$ are the lumped mass of propeller, the lumped mass of coupling, the length of shaft, Young’s modulus, the density of the shaft, the cross-sectional area of the shaft, respectively:

7

T = T_{5} T_{4} T_{3} T_{2} T_{1} = [\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}],

8

T_{1,5} = [\begin{matrix} 1 & 0 \\ - M_{p, c} ω^{2} & 1 \end{matrix}],

9

T_{2,4} = [\begin{matrix} \cos (τ l) & \frac{\sin (τ l)}{E A τ} \\ - E A τ \sin (τ l) & \cos (τ l) \end{matrix}], τ = \frac{ω}{\sqrt{E / ρ_{s}}} .

When the load $f_{0}$ is acted on the propeller, the relationship between state vectors of the right and left ends of the shafting system is presented in Eq. (10). Substituting the free-free boundary conditions ( ${F_{1}}^{l} = {F_{5}}^{r} = 0$ ) into Eq. (10), the state vector of the propeller end can be obtained by solving the Eq. (10), shown as Eq. (11). Utilizing the state vector of the propeller end and the accumulated transmission matrix from propeller to the component $i$ , the response at any component along the shaft could be obtained:

10

\{\begin{matrix} U_{5}^{r} \\ F_{5}^{r} \end{matrix}\} = [\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}] \{\begin{matrix} U_{1}^{l} \\ F_{1}^{l} - f_{0} \end{matrix}\},

11

\{\begin{matrix} U_{1}^{l} \\ F_{1}^{l} \end{matrix}\} = \{\begin{matrix} - \frac{T_{22}}{T_{21}} f_{0} \\ 0 \end{matrix}\} .

The force transmissibility through the thrust bearing foundation could be easily obtained by ${F_{b}}^{r} / f_{0}$ .

3. Discussions of results

The corresponding configuration data of the thrust bearing are load $F =$ 200 kN, shaft speed $n =$ 220 r/min, $r_{2} =$ 0.24 m, $r_{1} =$ 0.125 m, $m =$ 8, $θ_{0} =$ 0.611 rad, $r_{p} =$ 0.186 m, $θ_{p} =$ 0.3543 rad. The corresponding configuration data of the shaft are $l_{1} =$ 14 m, $l_{2} =$ 2 m, the diameter of the shaft $d =$ 0.16 m, $M_{p} =$ 7000 kg, $M_{c} =$ 1000 kg, $ρ_{s} =$ 760 kg/m³, $E =$ 200 GPa. The corresponding configuration data of the RC are $d_{0} =$ 60 mm, $d_{1} =$ 5 mm, $V_{1} =$ 1.6 L, $L_{1} =$ 2 m, $ρ_{1} =$ 760 kg/m³, $B_{1} =$ 1940 MPa, $μ_{1} =$ 0.23 pa·s.

Fig. 4 is the contrast figure of the force transmissibility through the thrust bearing foundation before and after a RC is attached to the thrust bearing. Fig. 4(a), Fig. 4(b), Fig. 4(c) and Fig. 4(d) exhibit the influences of the volume of the oil reservoir $V_{1}$ , the diameter of the piston cylinder $d_{0}$ , the length $L_{1}$ and diameter $d_{1}$ of the oil pipe, respectively.

Compared with the situation in absence of the RC, the introduction of the RC results in the elimination of the dominant peak at the original 1st natural frequency and alteration of the 2nd natural frequency much more towards the high frequency direction. Simultaneously, it also introduces another two dominant resonance peaks around the original 1st natural frequency. The amplitudes and locations of the two peaks are related to the different parameters of RC, but both of the amplitudes are lower than the original one. Off resonance frequency, there is little difference between the situations with and without a RC, which proves that the RC only exhibits good performance over a narrow frequency bandwidth.

As shown in Fig. 4(a), with the increasing of $V_{1}$ , $K_{h}$ and $F_{h}$ decrease while $M_{h}$ , $C_{h}$ stays invariable. The peak on the right side moves towards the original 1st natural frequency and the amplitude of the peak increases. As shown in Fig. 4(b), with the increasing of $d_{0}$ , $M_{h}$ , $K_{h}$ and $C_{h}$ decrease while $F_{h}$ stays invariable. The two peaks move together towards the original 1st natural frequency and the amplitudes of the two peaks stay nearly equal and decrease gradually. As shown in Fig. 4(c), with the increasing of $L_{1}$ , $M_{h}$ and $C_{h}$ increase and $F_{h}$ decreases while $K_{h}$ stays invariable. The peak on the right side moves towards the original 1st natural frequency and the amplitude of the peak increases. As shown in Fig. 4(d), with the increasing of $d_{1}$ , $M_{h}$ and $C_{h}$ decrease and $F_{h}$ increases while $K_{h}$ stays invariable. The peak on the right side moves towards the high frequency direction and the amplitude of the peak decreases.

From above analysis, it is obvious that the peak on the right side is attributed to the RC, while the peak on the left side is due to excitation of the original shafting system. It could be concluded that, with the decreasing of $F_{h}$ (increasing of $M_{h}$ or decreasing of $K_{h}$ ), the influences of the RC on the longitudinal vibration of the shafting system is more and more significant. And that is why the two peaks moves and changes synchronously when $F_{h}$ stays invariable. It could be foreseen that, when $V_{1}$ is small enough, $K_{h}$ will be infinite, so the RC could be regarded as a rigid support. As a result, the peak on the left side overlaps the original peak at 1st natural frequency, while the peak on the right side disappeared. When $L_{1}$ is long enough or $d_{1}$ is small enough, $M_{h}$ will be infinite. As a result, the peak on the right side will overlap the original peak at 1st natural frequency, while the peak on the left side disappeared. Be careful, because of the limitation of the axial shaft movement, $K_{h}$ should not be too small.

Considering the mass, stiffness and the 1st natural frequency of the shafting systems, optimizing $V_{1}$ , $d_{0}$ , $L_{1}$ , $d_{1}$ to acquire a natural frequency of the RC which is close to the original 1st natural frequency of the shafting system, a appropriately large virtual mass, a appropriately small virtual stiffness and a appropriate virtual damping, there will be a good effect of vibration reduction when the RC is attached to the shafting system.

Fig. 4Effect of RC with variations in designing parameters on force transmissibility

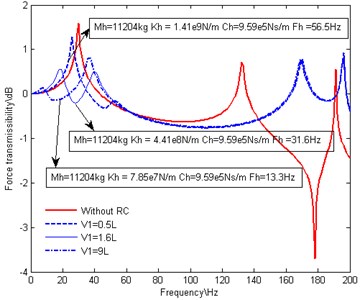
a) Variations in the volume of the oil reservoir

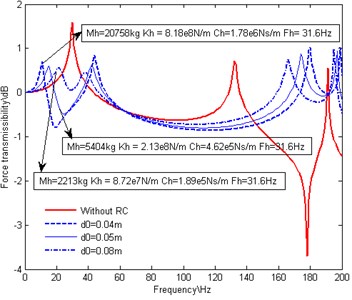
b) Variations in the diameter of the piston cylinder

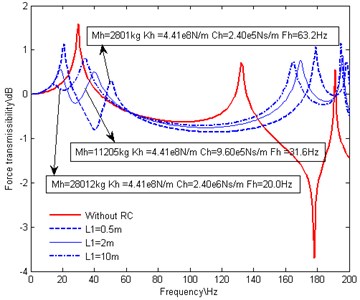
c) Variations in the length of the oil pipe

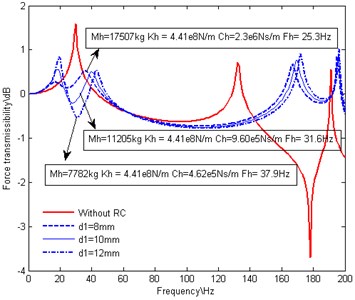
d) Variations in the diameter of the oil pipe

4. Conclusions

In this paper, force transmissibility through the thrust bearing foundation for different cases is employed to study the dynamic behavior of the RC as well as its influences on the longitudinal vibration of the propulsion shafting system. The conclusions can be summarized as follows:

The introduction of the RC eliminates the resonance at low frequency suffered previously and introduces another two resonance peaks around original 1st natural frequency, as well as significantly lowering the maximum response compared with the original peak. The peak on the right side is attributed to the RC, while the other is due to excitation of the other shafting system components. Furthermore the resonance frequency of the 2nd natural frequency moves towards the high frequency direction and the peak value nearly stay invariable. Such variations in force transmissibility characteristics are linked with the variation of the designing parameters of the RC, such as the diameter of the piston cylinder, the diameter of the oil pipe, the length of the oil pipe, the volume of the oil reservoir. By optimizing above parameters, the purpose of reducing severe longitudinal vibration and its transmission into the hull through a thrust bearing over a specified frequency range would be realized.

References

Zhang G. B., Zhao Y., Li T. Y. Propeller excitation of longitudinal vibration characteristics of marine propulsion shafting system. Shock and Vibration, 2014, p. 1-19.

Search CrossRef
Pan J., Farag N., Lin T., Juniper R. Propeller induced structural vibration through the thrust bearing. Proceedings of Acoustics, Australia, 2002, p. 390-399.

Search CrossRef
Dylejkoa P. G., Kessissogloua N. J., Tsob Y., Norwoodb C. J. Optimization of a resonance changer to minimize the vibration transmission in marine vessels. Journal of Sound and Vibration, Vol. 300, Issues 1-2, 2007, p. 101-116.

Search CrossRef
Goodwin A. J. H. The design of a resonance changer to overcome excessive axial vibration of propeller shafting. Transactions of Institute of Marine Engineers, Vol. 72, 1960, p. 37-63.

Search CrossRef
Shapiro W., Graham R., Anderson G. Predicted performance characteristics of hybrid fluid-equalized tilting-pad thrust bearings. Journal of Lubrication Technology, Vol. 105, 1983, p. 476-483.

Search CrossRef
Jang G. H., Kim Y. J. Calculation of dynamic coefficients in a hydrodynamic bearing considering five degrees of freedom. Journal of Tribology, Vol. 121, 1999, p. 499-505.

Search CrossRef

About this article

Received

Accepted

28 August 2015

Published

18 September 2015

SUBJECTS

Mechanical vibrations and applications

Keywords

resonance changer

longitudinal vibration

shafting system

transfer matrix method

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.