Planetary gearbox remaining useful life estimation based on state space model

1. Introduction

Remaining useful life (RUL) estimation is an essential part in prognostics and health management (PHM) [1]. If the RUL prediction is accurate, it is very helpful for conditio-based maintenance (CBM). Numerous prognostic approachs have been proposed to predicte RUL and reported in technical literatures. Data-driven approach is one of the main methods for RUL estimation [2]. The data-driven method is derived directly from collected history data or performance data [3].

Most failure mechanisms can be traced to an underlying physical or chemical degradation process [3], such as crack growth and wear. However, in many engineering cases, it is difficult (or even impossible) to directly measure the system degradation state. As a result, sensor signals are usually collected to characterize the degradation process [4]. State space model is one of the approaches that can be used to establish the relationship between system degradation states and sensor signals [5].

In this paper, a state space model based on Gamma process is proposed to predicte RUL for planetary gearbox. And a planetary gearbox life-cycle experiment is done to obtain the degradation data and verify the effectiveness of the proposed method.

2. State space model based on Gamma process

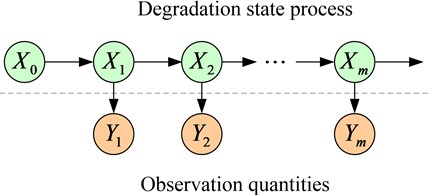
Some system degradation states cannot be directly observed, but some observation quantities can be achieved through sensors. These observation quantities, to some extent, reflect system degradation state. State space model can established the relationship between system degradation states and observation quantities, as shown in Fig. 1.

For the convenience of calculation, the state space model is simplified in this paper, it is written as:

where $y_i$ is the observation quantity for degradation state $x_i$. $F_i\left(\right)$ is the state evolution function, $H_i\left(\right)$ is the observation function. ${\theta }_1$, ${\theta }_2$ are function parameters and $\zeta$, $\epsilon$ are noises for state evolution function and observation function, respectively.

As Gamma process has the properties such as stable and independent increment, it is suitable for describing monotonic degradation [6, 7]. System degradation process is assumed to be Gamma distribution in this study. In other words, the degradation process of system is considered to be smooth Gamma process, the shape-parameter is $\eta \left(t\right)=at\text{,}$ the observation function is $y=c\cdot x+\epsilon$. The system degradation state space model can be expressed as:

When the observation noises are assumed to be normal distribution and the expectation is 0, the observation quantity $y~N(cx,\sigma )$. Therefore, the system degradation state space model can be determined after estimating the parameters $a$, $\xi$, $c$, $\sigma$.

Fig. 1The relationship between system degradation state and observation quantity

a)

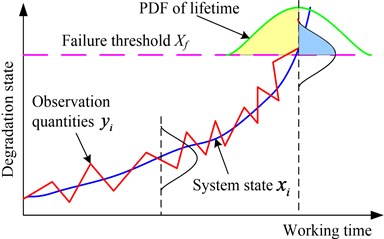
b)

3. Model parameters estimation

Because of the difficulty of state data collection, the system degradation state data maybe missing and incomplete. Experience maximization (EM) can avoid the disadvantage factors in the process of model parameters estimation.

$X_f$ is the failure threshold of system degradation quantity, $T_f$ is the working time that degradation quantity exceeds failure threshold $X_f$. By the nature of Gamma distribution, it can be achieved as follows:

It can be known from observation function that:

If the model parameter $a$ is given initial value $a^{\left(0\right)}$, other initial parameters can be obtained from Eqs. (3)-(7) as follows:

To facilitate the description, let $\theta =({\theta }_1,{\theta }_2)$, ${\theta }_1=(a,\xi )$, ${\theta }_2=(c,\sigma )$. ${\theta }^{\left(l\right)}$ is the initial parameter of $l$th step cycle, the expectation of complete likelihood function can be written as:

By the maximizing solution conditions, it can be known that $Q\left(\theta |{\theta }^{\left(l\right)}\right)$ is maximal when $\partial Q\left(\theta \right|{\theta }^{\left(l\right)})/\partial \theta =0$. ${\theta }^{(l+1)}$ can be expressed as follows:

Put ${\theta }^{\left(l\right)}$ and ${\theta }^{(l+1)}$ into the Eq. (11), if it satisfies the convergence condition, the optimal parameter is obtained $\widehat{\theta }={\theta }^{(l+1)}$; if it does not satisfy the convergence condition, let ${\theta }^{(l+1)}$ as the initial parameter of ($l+$1)th step cycle for EX algorithm until the the convergence condition is satisfied.

It can be known from Eqs. (12)-(15) that parameter ${\theta }^{(l+1)}$ can be determined as long as $E\left(x_i\right)$, $E\left({\left(x_i\right)}^2\right)$ and $E\left(\mathrm{l}\mathrm{n}\right(x_i-x_{(i-1)}\left)\right)$ are obtained. However, there are only a small number of degradation state quantity x can be achieved in actual condition monitoring process. And the degradation state quantity x has certain uncertainty. Therefore, $E\left(x_i\right)\text{,}$$E\left({\left(x_i\right)}^2\right)$ and $E\left(\mathrm{l}\mathrm{n}\right(x_i-x_{(i-1)}\left)\right)$ can be estimated by particle filter (PF) [8, 9] and the result are shown as follows:

where $x_i^s$ is the $s$th particle of $x_i$, and $w_i^s$ is the weigths of $x_i^s$.

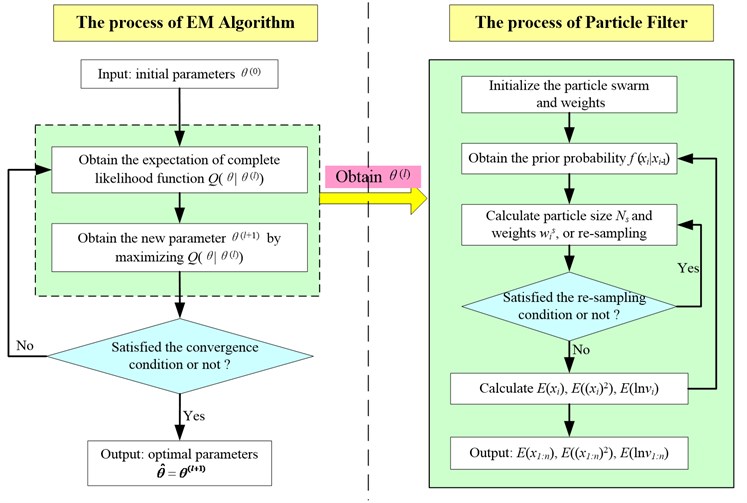
The process of state space model parameter estimation is shown in Fig. 2.

Fig. 2The process of parameter estimation

4. System RUL

After model parameter estimation, the system RUL can be predicted. The cumulative distribution function (CDF) of system RUL is:

And the probability distribution function (PDF) of system RUL is:

The expection of system RUL is:

5. Planetary gearbox RUL estimation

A case study is carried out for predicting planetary gearbox RUL based on state space model. In order to validate the effectiveness of the method this paper proposed, a planetary gearbox life-cycle experiment has been done to obtain the degradation data that a planetary gearbox ran from new to failure.

As shown in Fig. 3, the experiment rig consists of a test planetary gearbox, a 4 Kw drive motor, a speed and torque sensor and a magnetic powder brake. And between the two of them is connected by coupling. There are four accelerometers fitted onto the casing of gearbox to record vibration data, as shown in Fig. 4. In the experiment, the sampling frequency is 20 kHz. The speed of the gearbox is 1000 rpm. The magnetic powder brake provide about 340 Nm to reduce the lifetime of gearbox. Each vibration monitoring provides a date file collected in 12 seconds at every 5 minutes, twelve groups of date files are collected in every hour. The total experimental time is 680 hours. As shown in Fig. 5, the energy of vibration signals of the first 640 h is presented, and also some wear quantities of the first 680 h is shown.

Fig. 3Planetary gearbox experiment rig

Fig. 4Mounted location of accelerometers

Fig. 5Energy of vibration signals and wear quantities

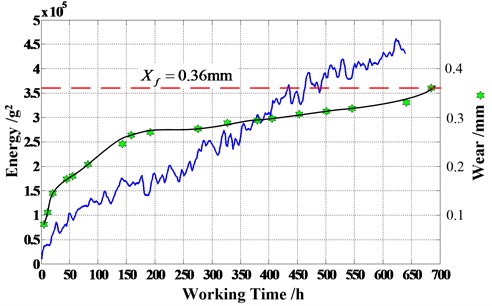
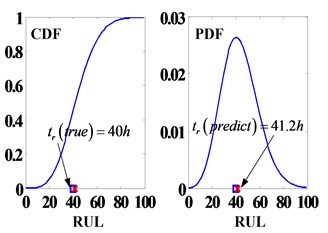
The wear quantity in 680 h is 0.36 mm, set it as failure threshold, $X_f=$0.36 mm. Using the proposed method to predict planetary gearbox RUL when working time is 640 h. The result of parameters estimation is shown in Fig. 6 ($a=$0.1755, $\xi =$315.1, $c=$8.985×10⁵, $\sigma =\mathrm{}$7.645×10⁴). The planetary gearbox RUL is $t_r\left(predict\right)=\mathrm{}$41.2 h. The CDF and PDF of RUL at 640 h is presented in Fig. 7. It is obviously that the RUL values of prediction and actual ($t_r\left(true\right)=\mathrm{}$40 h) is very vicinal. Therefore, the RUL estimation method prposed in this study is effective.

Fig. 6The process of parameter convergence

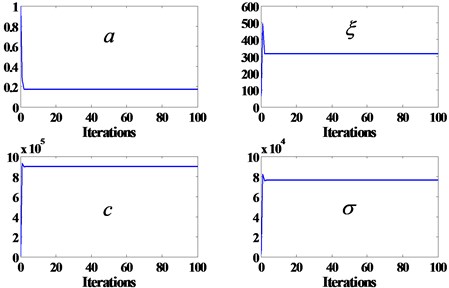
Fig. 7The CDF and PDF of RUL at 640 h

6. Conclusions

This paper is meant to investigate the RUL estimation method for planetary gearbox. A fault prognosis approach based on state space model is put forward. And experience maximization method and particle filter is used to estimate the parameters of state space model. The degradation data of a planetary gearbox life-cycle experiment is used to verify the effectiveness of the proposed method. And the RUL estimation result is satisfying.