Aerodynamic performance analysis of wind-sand flow on suspension bridge suspender cables

1. Introduction

China is one of the countries which suffer the most severe desertification in the world; 3.3 million km² land is suffering desertification in China [1-3]. Sandstorms are becoming the common phenomena for many regions in the midwest of China, and cause huge losses to the country every year. With the rapid economic development and increased road traffic in the midwest of China, the number of long-span bridges across rivers or canyons increases. The riding-type suspender cables are the main form for suspension bridge suspender cables. The suspender cables are one of the most important components for structural safety, and they are also most damageable during the construction period of the bridges [4]. The four strands not only impact the aerodynamic interference effect by the wind but also suffer from the influence of wind-sand flow on suspender cables, which cannot be disregarded.

Betti et al. [5] pointed out that ultimate ductility is controlled by the roughness of the geometry of the external surface of the wire when a galvanized wire is corroded, in their studies which focus on corrosion and embrittlement in high-strength wires of suspension bridge suspender cables. Mei et al. [6] investigated the structural measures for improving wind resistance stability of long-span suspension bridges with CFRP cables based on the Japan Akashi-Kaikyo Bridge, and the results show that the use of the CFRP cables can improve the wind resistance stability of suspension bridges. Zhang et al. analyzed the aerostatic instability mode of a three-tower suspension bridge named Maanshan Bridge based on the method of strain energy, and the results show that the changing rule of the total strain energy is dominated by the main cable and the initial wind attack angles [7]. Wang et al. [8] studied the three-dimensional flutter stability analysis of a triple-tower suspension bridge within the ANSYS and found that the effect of the cable system is prominent. Zhu et al. [9] studied the influence of the suspender cable’s parameters on vibration characteristics of a suspension bridge. However, the effect of wind-sand flow on the damage of suspender cables has not attracted enough attention of researchers.

The present work focuses on the law of aerodynamic interference effect of four cables of the riding-type suspender cables and the force of the wind-sand flow acted on the four cables. To address this problem, the wind-flow and wind-sand flow around the suspender cables of a suspension bridge are simulated within the FLUENT. Finally, the numerical simulation results are compared with the theoretical calculations based on a theoretical equation used in the wind-sand flow calculation for buildings in Jiang’s work [10]. All of these lay a foundation for the fatigue analysis of riding-type suspender cables of large-span suspension bridges.

2. The effect of the different sand volume fractions on the force on suspender cables

The riding-type suspender cables include the common cables, short cables, and long cables near the tower. Fig. 1 shows a common riding-type suspender cable. Given that the length of the cable is much larger than its diameter, the calculation problem of the flow field is approximately considered as a plane problem. Moreover, the suspender cables are made from four wire ropes with rough surface, and they are simplified as four cylinders in this work.

In Fig. 2, $U$ is the wind velocity and $\alpha$ is the wind attack angle. Four cables are named No. 1, No. 2, No. 3, and No. 4. The distance between No. 1 and No. 2 refers to the distance of the cables along the bridge, while the distance between No. 2 and No. 3 refers to the distance of the cables across the bridge. The diameter of every cable in the riding-type suspender cables is 60 mm.

Fig. 1A photo of the riding-type suspender cables

Fig. 2Diagram of the wind field around the suspender cables

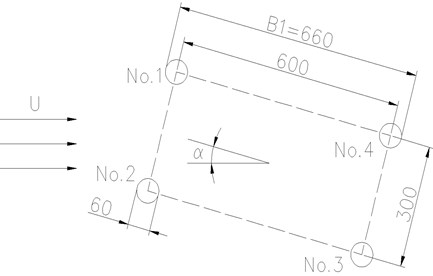
Fig. 3Computational domain for wind-sand flow around the riding-type suspender cables

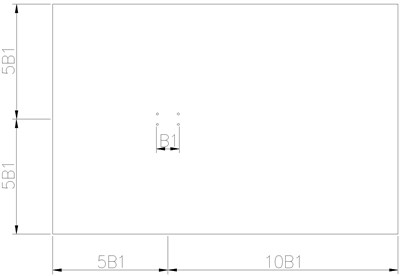
Fig. 3 shows the computational domain for wind-sand flow around the riding-type suspender cables; from Fig. 3, it can be seen the distances of the center of the riding-type suspender cables to the upstream boundary (5 B1), the downstream boundary (10 B1), the top and the bottom boundaries (both 5 B1). B1 is the distance of the two cables of the riding-type suspender cables in the direction across the bridge axis. The computational domain is divided into lots of grids; Fig. 4 shows that the minimum size of the grid is 0.0036 B1, and the total number of the grid is 181500.

Fig. 4Mesh of the wind-sand flow on the riding-type suspender cables

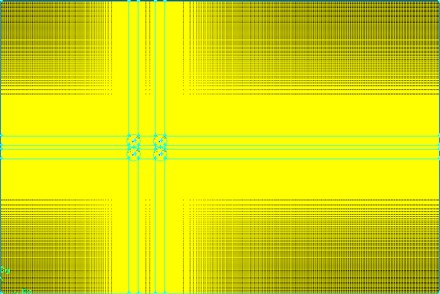
a) Mesh of the wind-sand flow field used in the calculation

b) The detailed figure of Fig. 4(a)

According to the wind resistance design regulations for highway bridges of China (JTG/T D60-01-2004), the entrance wind-sand flow speed is selected to be 20 m/s; the outlet boundary is free outflow; the surface of the suspender cable section is treated as no-slip wall boundary condition; the top and bottom boundary conditions are symmetrical. What's more, the sand volume fraction is introduced. The density of the sand is 2000 kg/m³, and its diameter is 5×10^-6 m. In consideration of the simplicity and stability of the simulation results, the mixture model is selected as a multiphase flow model.

Fig. 5a) Lift coefficients under the 0° wind attack angle; b) drag coefficients under the 0° wind attack angle

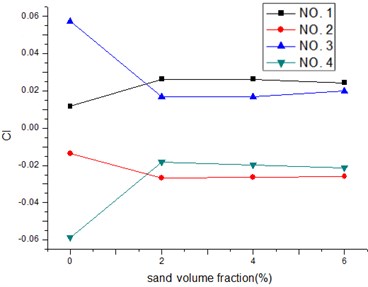
a)

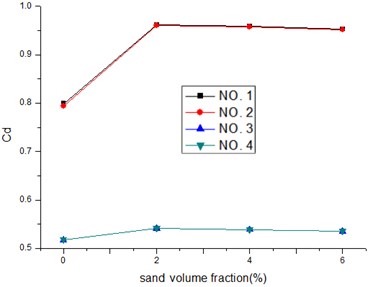
b)

Fig. 5 shows the lift and drag coefficients of the four columns (cables) in the wind-sand flow field with different sand volume fraction values under the 0° wind attack angle. From these results, it can be seen as follows:

1) The absolute values of the lift coefficients of the front columns (i.e. cables of No. 1 and No. 2) are larger with the introduction of the sand phase, while the lift coefficients almost remain the same level or only have a tendency to decrease slowly with the increase of the sand volume fraction.

2) With the increase of the sand volume fraction, the drag coefficients of the back two columns almost remain the same level.

3. Preliminary discussion of the results based on numerical simulation and theoretical calculation

A theoretical calculation of the wind load carrying the sands considers that the pressure on a building in a wind-sand region is equal to the sum of the net wind pressure and the impact pressure of the sands [10]:

where $\gamma$ is the specific weight of the air, $g$ is the acceleration of gravity, $v_1$ is the wind velocity, $\rho$ is the density of wind-sand flow and it is the product of the density of sand and the sand volume fraction, and $v_2$ is the leap forward speed of the sand. The first part in the Eq. (1) is the net wind pressure and the second part is the impact pressure of the sands. In engineering design, the leap forward velocity of the sand is considered the same with the wind velocity (i.e. $v_1=v_2$). The calculation error is acceptable in the engineering even though the momentum conservation is not met. Generally, consider $\gamma /2g$ is considered to be 1/1.6 [10], the Eq. (1) is simplified as follows [10]:

The density and speed of the wind-sand flow (when the sand volume fraction is 2 %) are substituted into Eq. (1), consider the density of sand is 2000 Kg/m³, and the calculation of the pressure is written as follows:

Without consideration of the effect of the sands, the pressure is calculated as follows:

With the lift and drag coefficients, the formula for pressure calculation of the wind-sand flow on the suspender cables is written as follows:

Table 1 shows the wind-sand flow pressure values under the different sand volume fractions based on the numerical simulation and the theoretical equation of Eq. (1). The numerical result is about 80 % of the theoretical result when there is no sand in the wind. However, when the structure is excited by the wind-sand flow, the numerical results are approximately one-quarter of the theoretical results. The reason is explained as follows: the velocity of sand is less than the wind velocity; however, the velocity of sand is considered the same with wind velocity in the theoretical calculation, which made the theoretical results much greater than the real values. Therefore, a suitable formula for pressure calculation of wind-sand flow on the suspender cables is still required to be further studied with consideration of numerical simulation, experiments and the on-site measurement.

4. Conclusions

The wind-sand flow field around the suspender cables of a long-span suspension bridge is simulated on the basis of the computational fluid dynamics within the FLUENT, and the following conclusions are summarized:

1) The forces of the back two columns of the riding-type suspender cables in the wind-sand flow field are approximately 0.5-0.7 times of the front two columns when the wind attack angle is 0°.

2) The sand volume fraction has an insignificant effect on the drag and lift coefficients of suspender cables but has a significant effect on the force exerted on the suspender cables. The force applied on the hangers increases with the increase of the sand volume fraction.

3) Based on the formula used for pressure calculation of the wind-sand flow on a building, the pressure of numerical results is about one-quarter of that using the theoretical calculation; therefore, a suitable theoretical formula for pressure calculation of wind-sand flow on the suspender cables is still required to be studied in further research.