A research on the dynamic characteristics of axially moving beam under thermal shock

1. Introduction

The axially moving system is a widely used structure in aerospace fields. For example, high-speed flight of missiles, rockets, artillery systems, these structures and their sub-structures are of characters with slenderness and axially moving, and all of them can be simplified into axially moving beams. Therefore, the study of lateral vibration characteristics and dynamic behavior has an important practical significance [1, 2].

Because of the power required, the engine and the windward side of the aircraft will suffer a more severe heating condition in the acceleration process. The temperature of the nearby beam structures rises sharply, which makes a higher temperature and temperature gradients. This sudden change of temperature caused by the thermal shock often induces a strong vibration response of the structure. A number of studies [3-5] have been performed for the thermodynamic properties of beam model, but most of them are for the problems in steady state temperature field. The vibration characteristics of axially moving beam under thermal shock are not much concerned. Li and Fan [6] studied the transient dynamic response of Timoshenko beams under thermal shock. Wang [7] researched the dynamic response and control of an axially moving beam with supersonic speed under thermal shock. These studies are based on the effect of thermal shock, but the effect of the axial movement of the beam model is not considered comprehensively. Chen and Chen [8] studied the dynamic characteristics of axially moving Timoshenko beam with compressive load. This work considered the effect of the axial movement, but the effect of the thermal shock is not discussed.

In summary, when the formers researched the issue of thermal shock, they did not consider the joint action of thermal shock and axial movement on the vibration characteristics of the beam structure. In this work firstly, based on the thermal shock model, the equivalent model is established. Secondly, according to Timoshenko beam theory and Hamilton principle, the governing equation of transverse vibration and boundary conditions are presented. Finally, the Differential Quadrature Method is applied to solve the transverse vibration problem. By simulating different thermal shock conditions, the effects of thermal shock and axial velocity to the dynamic characteristics of the beam model are researched.

2. Governing equations and boundary conditions

Fig. 1(a) shows the rectangular section beam, which is immovably simply supported at both ends. Considering the thermal shock effect, the temperature of the beam’s upper surface suddenly roses from $F_0$ to $F_u$ and keeps for a long time, meanwhile, the temperature of the beam’s lower surface suddenly roses from $F_0$ to $F_e$ and keeps for a long time. When $F_u=F_e$, because of the axial restraints of both ends, the axial expansion of the beam is restricted and the pressurized thermal axial force will be formed consequently. However, there is no thermal bending moment, because the temperature distribution is symmetric to the beam section’s axis. The force condition can be simulated by the equivalent model as shown in Fig. 1(b), where $N$ is the equivalent thermal axial force.

Fig. 1Establishment of the equivalent beam model

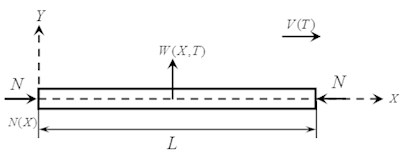
Fig. 2Model of axially moving Timoshenko beam under equivalent loads

Generally, the response of structure under thermal shock involves fluid-solid-heat multi-physical field coupling and so accurate analysis is very difficult. This work only examines the changes of the natural characteristics of the beam’s lateral vibration in thermal shock process, so two assumptions are established for the problem. The first assumption is the temperature along the direct of the beam’s height of the beam is identical everywhere, so it can be simplified to a one-dimensional instantaneous temperature field problem. The second assumption is the thermal shock process can be discretized into numerous independent states, and at each time it corresponds to a dynamic problem in which the equivalent thermal axial force $N$ applies on the Timoshenko beam.

As shown in Fig. 2, an axially moving Timoshenko beam travelling with speed $V\left(T\right)$, the displacement in the transverse coordinate is $W(X,T)$. The stiffness of its cross section is set as ($X$) and the shear stiffness is $\kappa GA$. $I_m\left(X\right)$ is the moment of inertia of cross section and $E$ is the modulus of elasticity. It is assumed that at a certain time the non-uniform temperature field of the beam which is under a thermal shock causes the equivalent thermal axial force $N$.

At a given time the total kinetic energy of the system is:

And the total potential energy of the system is:

According to Hamilton’s principle, the difference between the kinetic and potential energy is zero. The expression of governing equations for axially moving Timoshenko beam under thermal shock can be established based on the variational analysis, where for a uniform beam, $I_m\left(X\right)=\rho I$. Without considering the changes of axial force and axial velocity along the longitudinal direction, i.e. $\partial N/\partial X=0$ and $\partial V/\partial X=0$. So, by introducing the dimensionless parameters:

The partial differential equation of transverse vibration in dimensionless form is:

Similarly, the dimensionless boundary conditions can be obtained:

3. One-dimensioned instantaneous temperature field

This work adopts one-dimensional instantaneous temperature field under the second boundary condition [9], which assumes that the initial state of the axially moving beam is a rectangular section beam in the case of thermal equilibrium. The expression of governing equations and boundary conditions for the heat conduction are:

where $F$ presents temperature, $T$ is the time, $C$ is heat capacity, $\rho$ is density of beam material, $K$ is thermal conductivity, $h_r$ is heat transfer coefficient, $H$ is the height of the rectangular section beam. The general solution in the form of separation of variables can be expressed as:

where $a^2=K/C\rho$.

In addition, elastic modulus and other mechanical parameters of the material will change in the thermal environment and the thermal softening effect will appear. The literature [10] shows that elastic modulus $E^F$ at temperature $F$ can be expressed as:

where the temperature-rise coefficient is ${\alpha }_E=$–4×10^-4. The mechanical parameters of beam material need to be corrected, so the average elastic modulus and the average shear modulus are respectively used as the elastic modulus and shear modulus of the beam:

So, the formula for thermal axial force is:

4. Approximate solution

Equation (3)’s general solution in the form of separation of variables can be expressed as:

where, $\varphi$ is the mode shape function, $\lambda$ denotes the natural frequency of beam. Substituting Eq. (11) into Eq. (3) and Eq. (4) yields:

According to the differential quadrature method, $r$th order derivative value of function $f\left(x\right)$ at point $x_i$ can be expressed as a weighted sum of the value of all the nodes [11]:

where, $A_{ij}^{\left(r\right)}$ presents the $r$th order weight coefficients of derivative, $f_j$ is the function value at $x_j$, $n$ is the number of nodes.

According to the interpolation principle the Lagrange interpolation polynomial is adopted to determine the weight coefficients. Eq. (12) can be translated to the matrix form as:

So, solving of Eq. (15) is transformed to the generalized eigenvalue problem. The eigenvalues of Eq. (15) represents the dimensionless natural frequency of beam system.

5. Numerical example analysis

An axially moving beam with rectangular section is used for solutions and discussions, it’s configuration and material parameters are: $L=$1 m, $H=$0.04 m, $D=$0.03 m, $E_0=$70 GPa, $\mu =$0.3, $\rho =$2.7×10³ kg/m³, and initial temperature $T_0$ is equal to ambient temperature. Table 1 shows the thermal parameters of structural material.

According to Eq. (7), the temperature distribution function along the direction of the height can be calculated. Fig. 3 shows the temperature profile of each time when the heat inputs of upper and lower surfaces are 100 centigrade. It can be found that in the initial moment of thermal shock loading the upper and lower surfaces’ temperatures quickly reach the temperature of heat input, while the middle of the region remains the initial temperature.

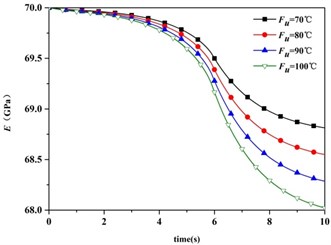
When the temperature of entire section increases gradually, the thermal softening effect will appear and lead to the decrease of elastic modulus. Therefore, it will cause the stiffness degradation of the material. The modified elastic modulus’ variation with time in the case of different heat input can be calculated by Eq. (9), just as Fig. 4. With the heat conduction, it can be found that the greater the heat input, the more decrease of elastic modulus decreases at the same time.

Fig. 3Temperature vs. position in the thickness direction and time (Fu=Fe= 100 °C)

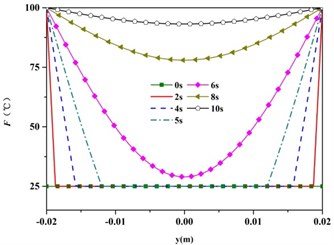
Fig. 4Elastic Modulus vs. time and heat input

According to Eq. (10), we obtain the distribution of the thermal axial force versus time. Fig. 5 shows the time response curve of thermal axial force in the case of different heat input. Seen from the distribution, the greater the thermal shock, the greater the thermal axial force generates.

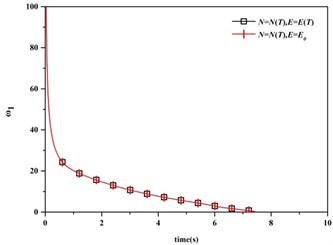
In order to study the main influence factors of the natural frequencies under thermal shock, Fig. 6 shows the comparison of 1st natural frequency under the two conditions, where the first condition is an actually thermal condition and the second condition is an assumption condition without the changing of elasticity modulus. It can be found that the coincidence of these two curves is very good. Looking at the distribution of the second condition, the natural frequency decreases with the increasing thermal axial force. When the loads formed by thermal shock reaches the critical load of the beam, the first order buckling mode will appear. On the basis of the above analysis, under this slight thermal shock, the thermal axial force plays a dominant role to the natural frequencies of the beam, while the changing of elasticity modulus plays a secondary role.

Fig. 5Thermal axial force vs. time and heat input

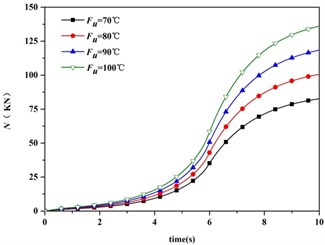
Fig. 61st natural frequency vs. time and different factors (Fu=Fe= 100 °C, v= 0)

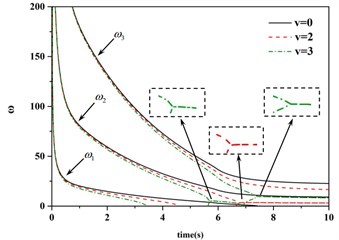
With the introduction of axial velocity, the effect of axial velocity to the dynamic characteristics of the axially moving beam is studied. Fig. 7 shows the first three natural frequencies versus time. The first natural frequency of the beam reduces with the time and reaches the first-order instability mode quickly. And after the first-order elastic mode reaches the critical state, the adjacent modes will couple when the axial velocity increases to a certain value. The greater the axial velocity, the earlier the coupling time appears. At this time, the beam is in a harsh state that the axial velocity and the thermal shock act together; As a result, the combined effect of the two factors makes the natural frequency of the beam decrease and reach the unstable state more easily.

Fig. 7The first three natural frequencies vs. time and speed (Fu=Fe= 100 °C)

6. Conclusions

In this paper, a dynamic model of axially moving beam is established based on Timoshenko beam theory, and the beam model is immovably simply supported at both ends and subjected to a thermal shock. Results of the study can be summarized as follows:

The thermal shock produces the thermal axial force and makes the elastic modulus of the beam decrease. The combined action of the elastic modulus and the thermal axial force affects the dynamic characteristics of the beam.

For slight thermal shock, the greater the thermal shock, the more quickly the natural frequency of the beam reduces. Correlated analysis showed that for the immovably pinned-pinned boundary condition the thermal axial force plays a dominant role to the natural frequencies of the beam, while the changing of elasticity modulus plays a secondary role.

The greater the axial velocities, the more quickly the natural frequencies of the beam reduce and the faster the 1st natural frequency reaches the first-order instability mode. The adjacent modes will couple when the axial velocity increases to a certain value, at this time, the beam is in a harsh state that the axial velocity and the thermal shock act together.