Frequency domain analysis of multiple modules-offshore mobile platform

1. Introduction

Multiple modules-offshore mobile platforms can be a sea comprehensive supply base with refueling, aircraft movements, logistics and other functions. More importantly, it can be used to protect national maritime rights. Therefore, it set off research upsurge of very large floating structures in international ocean engineering. Scholars from all over the world have spread a lot of theories of very large floating ocean structure [1-3]. Japanese scholars study pontoon offshore platforms and test the feasibility of floating platform [4-7]. Compared with Japan, the United States put forward the semi-submersible offshore base and related research [8-9]. Xu Daolin [10] set up a rigid-soft coupling network system. But it is only analyzed the one-dimensional network mechanics system composed of single direction connection. This paper will be based on the AQWA to analyze two-dimensional floating network system. This work provides a new methodology and an application example in the study for network structural dynamics, including very large scale floating structures.

2. Theory and models

2.2. Geometry and environmental parameters

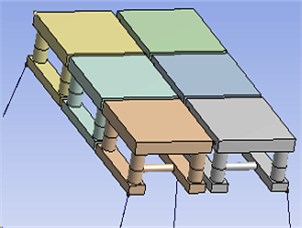
Multiple modules-offshore mobile platform is composed of six same models through cable and Fender, as shown in Fig. 1. Denoting $k$ as the mooring line stiffness and $L_0$ as its initial unstretched length, and $X_1\left(t\right)$, $X_2\left(t\right)$ as the attachment points on the two structures (in the fixed reference axes, where one structure may be a fixed location, for instance an anchor point), the tension on the mooring line is defined as:

7

$T=\left\{\begin{array}{ll}k\left(L-L_0\right),& L>L_0,\\ 0,& L\le L_0,\end{array}\right.$

where the stretched length of the cable is $L=\left|X_1\left(t\right)-X_2\left(t\right)\right|$.

Fig. 1Multiple modules-offshore mobile platform

The magnitude of the fender axis-directional compression force is defined as a polynomial function of the compression, as:

8

$T=\left\{\begin{array}{ll}{k}_1∆L+k_2{{\left(∆L\right)}^2+k}_3{\left(∆L\right)}^3{+k}_4{\left(∆L\right)}^4+k_5{\left(∆L\right)}^5,& ∆L>0,\\ 0,& ∆L\le 0,\end{array}\right.$

where $k_j$ ($j=$ 1, 5) are the coefficients of the polynomial function and $∆L=L_0-L$.

The main characteristic parameters of a single module is shown in Table 1. This paper adopts a once-in-a-century extreme condition in South China Sea, as shown in Table 2.

Table 1The main characteristic parameters of a single module

Parts	Parameters size
Deck (length $X$ width $X$ height) (m)	100×100×14
Pillar (high $X$ diameter) (m)	35×17
Buoy (length $X$ width $X$ height) (m)	100×18×10
Beam pillar (diameter) (m)	8
Other parameters	Normal waterline 25 m
	Displacement46440e3 m3
	$I_{xx}=$ 7.91e10 (kg∙m2)
	$I_{yy}=$ 6.49e10 (kg∙m2)
	$I_{zz}=$ 9.35e10(kg∙m2)
	Center of gravity from the waterline 5.0 m

Table 2Environmental loading conditions of South China Sea

	Parameters	The numerical
The waves	Significant wave height /m	13.5
	Peak period/s	15.5
	Angle / (°)	180 or 225

3. Frequency domain analysis

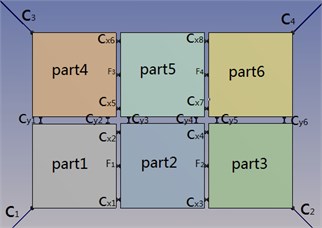
Due to large amounts of data, the paper selectedpart1 constrained by the anchor and part5 located in the central position of the chain structure to analyze. There is little literature research double row floating structure system, so this paper focuses on the lateral cables $C_{y1}$-$C_{y6}$, study how the two floating bodiescoupling in the lateral.

Fig. 2The amplitude of horizontal swing and the heave for part1

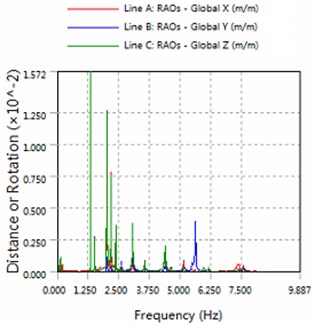
a) 180 degree angle for wave

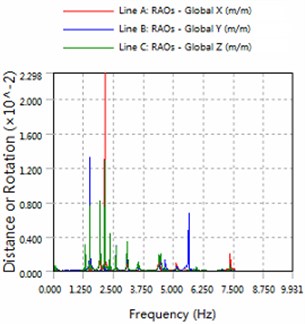
b) 225 degree angle for wave

By analyzing Figs. 1 to 7, can be obtained summary:

1) In the same sea conditions, part5 motion response amplitude is greater than part1. Because part1 constraints by the anchor, so it is realistic.

2) The platform is sensitive to the wave frequency of 1.25 Hz-7.5 Hz range. In engineering application, we prevent the frequency of this region to damage multiple modules-offshore mobile platform.

3) The magnitude of floating structure and cable and fender at wave of 180 degree angle are less than the magnitude at wave of 225 degrees. Therefore, in engineering applications, modules-offshore mobile platform should give more consideration to against the waves to arrange.

Fig. 3The amplitude of roll, pitch and the yaw for part1

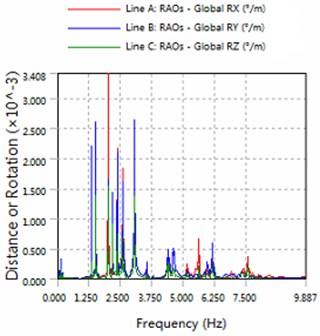
a) 180 degree angle for wave

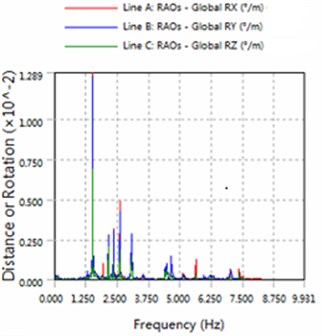
b) 225 degree angle for wave

Fig. 4The amplitude of horizontal swing and the heave for part5

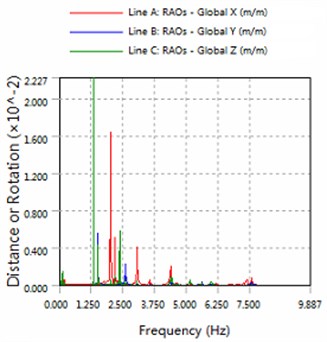
a) 180 degree angle for wave

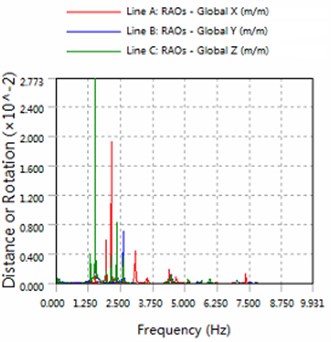
b) 225 degree angle for wave

Fig. 5The amplitude of roll, pitch and the yaw for part5

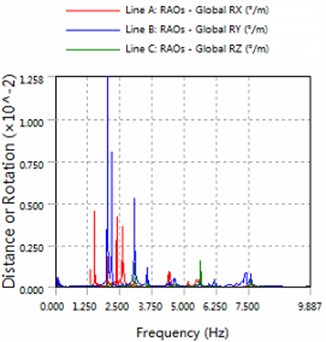
a) 180 degree angle for wave

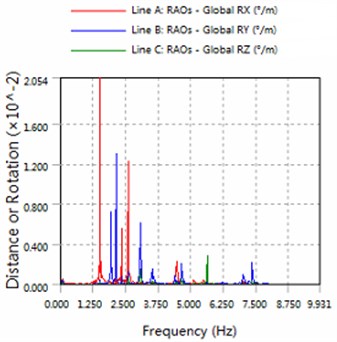
b) 225 degree angle for wave

Fig. 6The amplitude of cable force

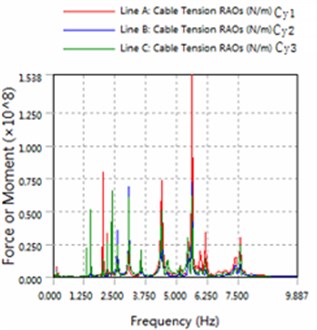
a) 180 degree angle for wave

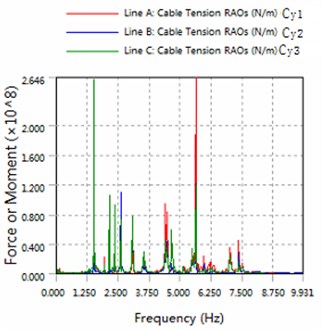
b) 225 degree angle for wave

Fig. 7The amplitude of fender force

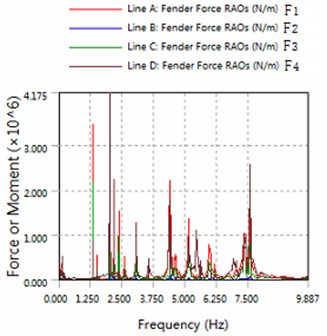
a) 180 degree angle for wave

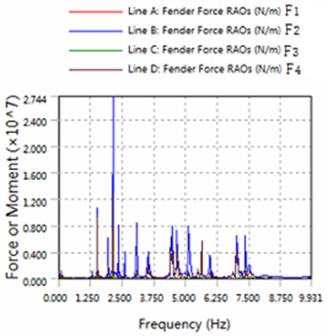
b) 225 degree angle for wave

4. Conclusions

At present few literature study multi-row and multiple modules-offshore platform, this paper use AQWA for frequency domain analysis of this platform. And preliminary results are obtained. Frequency domain analysis can get exact solution quickly and can provide the reference that whether designers decided to improve the system. This work provides a new methodology and an application example in the study for network structural dynamics, including very large scale floating structures.