Abstract
An adaptive algorithm with variable step size was firstly established in the paper in order to predict fatigue life of steel bridge welded components accurately and efficiently. The coupled damage constitutive model is developed within ABAQUS through user defined material subroutines to introduce damage revolving formulation into the fatigue damage analysis and the fatigue damage evolution process of the steel bridge components was finally studied. It is demonstrated that the adaptive variable step size algorithm for predicting fatigue life of steel bridge components is scientific and effective. Secondary development based on commercial software is more convenient and suitable to explore the mechanism of local damage accumulation process of various structures. The efficiency of the adaptive algorithm is not so high when the material damage is described by the linear Miller criterion, while it can effectively improve the calculation speed when the nonlinear Lemaitre damage evolution criterion is applied.
1. Introduction
The performance of the structures is nonlinear and the evolution of the meso-damage will aggravate the performance of the structure [1]. Recently, many researches on structural fatigue damage based on damage mechanics theory have been done [2-5]. The linear Miner’s law is widely used in fatigue life prediction and fatigue damage accumulation estimation [6]. Another damage evolution law for metal is suggested by Lemaitre, Chaboche, in which the damage variable evolves with respect to the stress and damage state [7, 8]. Many fatigue damage calculation methods based on finite element method are established with the development of the commercial finite element software. And these methods can be classified into two categories, one is called uncoupled damage method and the other is called coupled damage method. The interaction between the stress field and the fatigue damage field is ignored in the uncoupled damage method. However, the interaction cannot be ignored in the process of accurate fatigue life estimation as meso-damage gradually evolved and will speed up the process of the degradation of the structures. The coupled damage methods take the interaction between the stress field and the fatigue damage field into account by change the material property gradually during the fatigue life calculation. Recently many coupled damage methods based on FEM method are established [9-13]. A damage mechanics additional load finite element method is developed for the fatigue problems by introducing an additional load caused by meso-damage into usual FEM analysis [11]. Step size control is easy to ensure the accuracy of calculation results in such method. However, load matrix should be modified in every step according to the damage state of the calculated structures which make the method hard to be implemented in commercial finite element software. Elastic anisotropic damage constitutive is coded through user defined material subroutine in ABAQUS to introduce damage revolving formation into the fatigue damage analysis of steel bridge components [9-10]. The implement of the method is based on secondary development of ABAQUS and the user defined material subroutine coded by FORTRAN77 can be easily used for similar structures, so it is convenient to be used in fatigue damage analysis on large engineering structures. However, step size should be defined before the analysis and cannot be changed in the calculation which indicated a small step size is needed in the analysis.
In the paper an adaptive algorithm with variable step size for the calculation of fatigue life was firstly established, the step size can be controlled according to the damage state of the structures in order to predict fatigue life accurately and efficiently. A coupled finite element fatigue damage theory and method was used to describe the nonlinear material damage evolution of steel components. Efficiently of the adaptive algorithm and the fatigue damage evolution process of the Tsing Ma Bridge components is then studied.
2. Nonlinear coupled fatigue damage model
In the paper a coupled damage constitutive is first established to study the fatigue damage evolution process of the steel bridge components. Two different fatigue damage accumulation formulation is introduced in here to describe fatigue damage evolution. One is linear Miner’s Law, and it is widely used in fatigue life prediction and suggested by BS 5400 Part 10 to be useful in fatigue damage accumulation for steel structures [6]. And the formulation can be expressed as follow:
where is the failure stress cycles under the constant amplitude stress cycle of , , are constants, is the probability factor. , , can be obtained by BS 5400 Part 10 [10]. In the paper, 1.23×1012, 0.592, 3.0.
The fatigue damage accumulation increment at each increment step can be determined:
where is the fatigue damage accumulation increment corresponding to at each Gauss point.
It can be seen from Eq. (2) that the damage is proportional to the failure stress cycles according to Miner’s Law. The other fatigue damage accumulation formulation is suggested by Lemaitre and Chaboche, in which the cumulative damage is nonlinear, the expression is shown as follow [7]:
It can be seen from Eq. (3) that the evolution of damage is related to the stress amplitude and the damage state of the structure.
3. Adaptive algorithm with variable step size
The failure stress cycle is proportional to the life of the structure when the stress cycles of structures are assumed to be the same in different years. The formulation of can be expressed from Eq. (3) as follow:
In order to calculate the fatigue life accurately, the fatigue life equation must be solved numerically. Backward Euler approximation is applied and the discrete counterparts of Eq. (4) read:
Backward Euler algorithm is an explicit algorithm, the accuracy of the numerical solution is related to the size of the calculation. The smaller the step size is, the smaller the error estimate is. It can be seen from Eq. (5) that the truncation errors in backward Euler approximation is (), which indicated that should be controlled to get the result.
It can be seen from Eq. (3) that the damage evolution is nonlinear and its rate is related to the damage state of the structures. Damage evolution rate is low in the early stage and the evolution rate increase gradually with the accumulation of meso damage. It indicated that a relative large step should be used to lower the computational cost at first stage while a relative small step should be applied to ensure the accuracy of the numerical solution at last stage.
Fig. 1Flow char of step size adaptive algorithm for nonlinear accumulation of fatigue damage
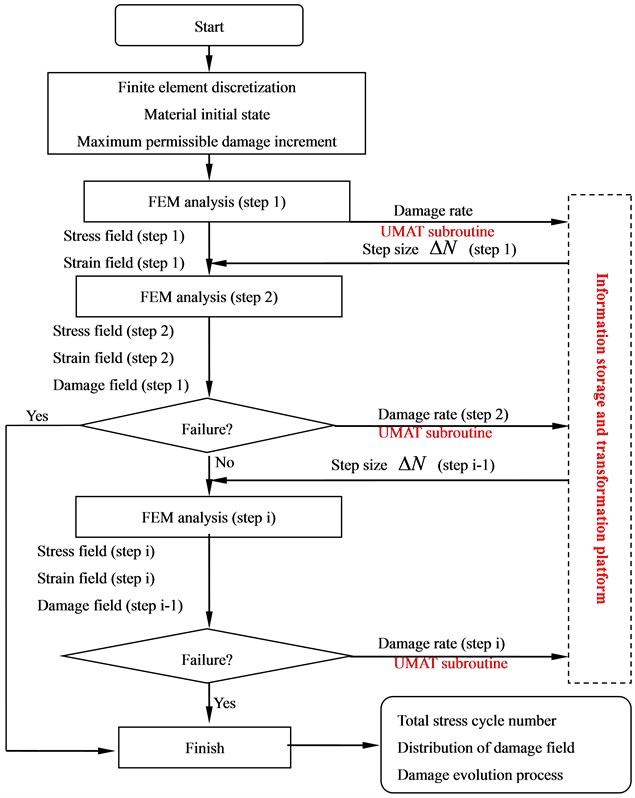
In the paper, the adaptive variable step size is expressed as follow:
where is the maximum permissible damage increment in one step, which is defined to ensure the accuracy of the numerical solution and is the maximum damage evolution rate of all material integral points:
In the section, a numerical approach is established for analyses on nonlinear fatigue damage accumulation of steel structures with adaptive step size. The user-defined material subroutine UMAT, supported in ABAQUS module, is developed. A specific supplemental software is coded by Python on the basis of the commercial software ABAQUS with its main flow chart shown as Fig. 1. There are two essential issues in the calculation, one is the implementation of constitutive equations coupled with evolving fatigue damage via UMAT, and the other is the information storage and transformation platform with adaptive variable step size. The key functions of the platform in th FEM step are (1) store damage evolution rate of all material integral points in ( 1)th step, (2) get the maximum value of damage evolution rate in ( 1)th step, (3) get from Eq. (6) and pass it as initial information to the th step.
4. Nonlinear fatigue damage accumulation in the steel girder of The Tsing Ma Bridge
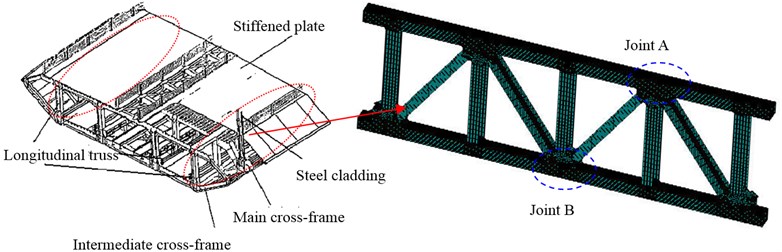
Different FEM models of the Tsing Ma Bridge are established [14] and the result shows that the longitudinal truss is the most critical fatigue damage components. So in the paper, the longitudinal truss is chosen as the research object shown as Fig. 2. The left chart in Fig. 2 is a typical steel box girder of Tsing Ma Bridge and the right chart is the FEM model of the longitudinal truss. The nominal stress amplitude spectrum is obtained from the strain time-history data output from the online health monitoring system of the corresponding details. Then stress concentration factor obtained from finite element analysis on local hot spot is applied here to transform the nominal stress amplitude spectrum into hot spot stress amplitude spectrum. Then fatigue damage accumulation is calculated with two different fatigue damage accumulation laws. The stress field of joint A and joint B is shown as Fig. 3 and Fig. 4, respectively. It can be seen that the maximum stress are located on the connecting region of inclined bar and cross rod. The result is consistent with the conclusion from related literature [10].
Fig. 2FEM model for longitudinal truss
The linear Miller’s law and Lemaitre nonlinear fatigue damage model are introduced into FEM analysis the fatigue life of the joint A and joint B, and the damage evolution of joint A and joint B is shown as Fig. 3 and Fig. 4 respectively. It can be seen from Fig. 3 and Fig. 4 that the damage of the material calculated with linear Miller’s law is higher compared with the Lemaitre nonlinear damage evolution especially in the early stage. In other words, the fatigue life predicted according to the linear Miller’s law is relatively conservative.
The fatigue life of joint A and joint B is calculated with adaptive step size (maximum permissible damage increment = 0.1) and fixed step size as shown in Table 1. It can be seen from Table 1 that fatigue life of joint A, B is almost the same when linear Miller’s law is applied, while the fatigue life of joint A, B with adaptive step size method is larger than that with fixed step size method when Lemaitre nonlinear fatigue damage formulation is applied. It is indicated that adaptive step size method is more useful if Lemaitre nonlinear fatigue damage model is applied.
In order to check the computational efficiency with the adaptive algorithm, computational cost and FEM steps for analysis on fatigue life of joint A and joint B is shown as Table 2. It can be seen that the number of FEM steps with the adaptive step size determined by the maximum damage increment is less than that with the fixed step size method, while the total time with the adaptive step size is not always less than that with the fixed step size method. Note that, the damage evolution rate and other dates should be written to file after every FEM step and the data stored in the file should be read before every FEM step. As is well known, the speed of reading information from files and writing information to files on the disks is much slower than that in memory, besides the degrees of freedom of FEM model for longitudinal truss is small and the computational time for every FEM step is short (no more than 2 s), so the time to read and write information cannot be ignored, and the actual efficiency with the developed adaptive algorithm is relative low. However the performance of the developed adaptive algorithm should be better for large structures as the number of the degrees of freedom of FEM model will be large.
Fig. 3Damage evolution of joint A
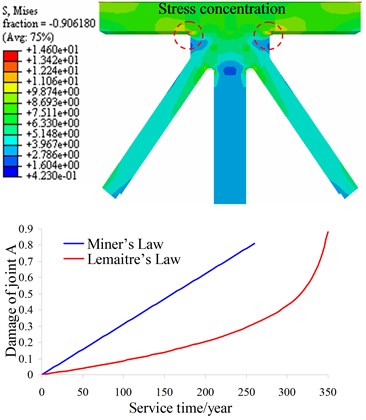
Fig. 4Damage evolution of joint B
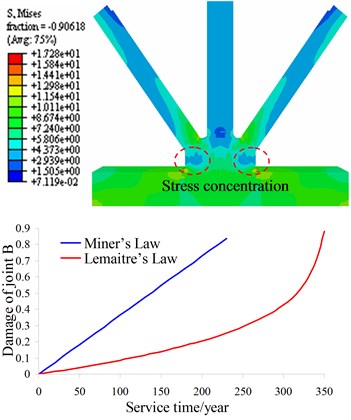
Table 1Fatigue life of joint A and joint B
Joint A | Joint B | |||
Fixed step/ year | Adaptive step/ year | Fixed step/ year | Adaptive step /year | |
Miner’s law | 256 | 254 | 219 | 220 |
Lemaitre’s law | 345 | 335 | 305 | 290 |
Table 2Computational cost and FEM steps for predicate fatigue life of joint A and joint B
Joint A | Joint B | |||
Fixed step | Adaptive step | Fixed step | Adaptive step | |
Miner’s law | 39 s/26 steps | 45 s/11 steps | 33 s/22 steps | 46 s/11 steps |
Lemaitre’s law | 53 s/35 steps | 46 s/11 steps | 47 s/31 steps | 45 s/11 steps |
5. Conclusions
An adaptive algorithm with variable step size for the calculation of fatigue life was firstly established in the paper. The coupled fatigue damage constitutive model is implemented via UMAT based on secondary development in ABAQUS. Fatigue damage evolution process and fatigue life of Tsing Ma Bridge components was finally studied with the developed adaptive algorithm. The result shows that the adaptive variable step size algorithm is scientific and effective and reduces the computational cost effectively. And the implement of the adaptive variable step size algorithm is relative easy and can be reused in fatigue damage analysis on other large span steel bridge. The results of steel components fatigue life obtained by using linear Miller criterion are conservative. The effect of the adaptive algorithm on calculation efficiency is not good when the material damage is described by the linear Miller criterion, while it can effectively improve the calculation speed when the nonlinear Lemaitre damage evolution process is considered.
References
-
Wu B. J., Li Z. X., Tang K. K. Multi-scale modeling and damage analyses of large civil structure multi-scale mechanics from material to structure. Advance in Mechanics, Vol. 37, Issue 3, 2007, p. 321-337.
-
Chen Z. P., Jiang J. L., Chen L. Research on fatigue interaction damage of steel 1.25Cr0.5Mo. Acta Metallurgica Sinica, Vol. 43, Issue 6, 2007, p. 637-642.
-
Jin J. P., Men G. On the fatigue-creep damage analysis of a steam turbine rotor by a nonlinear continuum damage mechanics model. Proceedings of the Chinese Society for Electrical Engineering, Vol. 23, Issue 9, 2003, p. 167-172.
-
Lin J. W., Zhang J. H., Zhang G. C. Study on fatigue damage of aero-engine blade based on non-linear continuum damage model. Journal of Mechanics Engeering, Vol. 46, Issue 18, 2010, p. 66-705.
-
Fan Z. C., Chen X. D., Jiang J. L. Cyclic creep and fatigue interaction CDM model of 16MNR steel. Acta Mechanica Solid Sinica, Vol. 27, Issue 1, 2006, p. 65-70.
-
BSI, BS5400, Part 10: Steel, concrete and composite bridges.1980
-
Lemaitre J. Formulation and Identification of Damage Kinetic Constitutive Equations, Continuum Damage Mechanics-Theory and Application. Springer-Verlag, New York, 1990.
-
Lemaitre J. A Course on Damage Mechanics. Spring-Verlag, 1992.
-
Zhou T. Q., Chen T. H. T. Fatigue damage analysis of long span steel bridge welded members using the finite element method and damage mechanics. Journal of Ship Mechanics, Vol. 2009, Issue 5, p. 739-747.
-
Li Z. X., Zhou T. Q., Chan T. H. T., Yu Y. Multi-scale numerical analysis on dynamic response and local damage in long-span bridges. Engineering Structures, Vol. 29, Issue 7, 2007, p. 1507-1524.
-
Tang X. S., Yang J. Y., Jiang C. P., Zhang X. Damage mechanics-additional load-finite element method for fatigue life prediction of axisymmetrical structural members. Acta Aeronautica et Astronautica Sinica, 2002, p. 97-101.
-
Wang C. M. Multi Objective and Multi Factor Correction Technique and Its Application in Multi Scale and Multi Scale Simulation. Southeast University, Nanjing, 2009.
-
Zhen X. D., Zhang X. Damage mechanics finite element method for prediction of total fatigue lives of metal structure members. Acta Aeronautica et Astronautica Sinica, Vol. 12, Issue 2, 1997, p. 1-9.
-
Chan T. H. T., Guo L., Li Z. X. Finite element modeling for fatigue stress analysis of large suspension bridges. Journal of Sound and Vibration, Vol. 261, 2003, p. 443-464.
