Transverse failure modes and control strategies of super long-span cable-stayed bridge under extreme earthquake

2.1. Analytical model based on energy balance

For a generic bridge structure with passively controlled under earthquake excitations, the following dynamic system of nonlinear equation can be written:

In which $\mathbf{X}$, $\dot{\mathbf{X}}$ and $\ddot{\mathbf{X}}$ are the relative displacement, relative velocity, and relative acceleration vectors, respectively; $\mathbf{M}$, $\mathbf{C}$ and $\mathbf{K}$ are the mass, damping, and time-varying stiffness matrixes, respectively; ${\ddot{x}}_g$ is the earthquake wave acceleration; $\mathbf{I}$ and $\mathbf{N}$ are the matrixes of assignment that refer the seismic and control forces to the associated degree of freedom; the forces vector, ${\mathbf{f}}_p$, generated by the passive devices, can be expressed in the following form:

In which ${\mathbf{K}}_d$ and ${\mathbf{C}}_d$ are the stiffness matrix and the damping matrix referred to the devices, respectively; whereas ${\mathbf{U}}_d$ and ${\dot{\mathbf{U}}}_d$ are the displacements and the velocity of the couples of nodes linked by the devices, respectively.

Both sides of Eq. (1) simultaneously multiply by ${\dot{\mathbf{X}}}^{T}dt$, in which $T$ denotes transposition of a vector $d\mathbf{X}$. The energy equation of bridge structure, can be defined by the integral with respect to the duration of earthquake wave, which can be written as follows:

In which $E_I$ is the total input energy, $E_K$ is the instantaneous kinetic energy, $E_D$ is the cumulative damping energy, $E_H$ is the cumulative hysteretic energy, $E_S$ is the instantaneous elastic strain energy. $E_{dD}$ and $E_{dH}$ are the cumulative damping energy and hysteretic energy referred to the passive devices, respectively. The vector, $E_I$, can be written as follows:

According to Eq. (1), the use of elasto-plastic analysis can yield the displacement, moment, and curvature vectors of bridge structure under given input waves, and can further gain the cumulative hysteretic energy dissipation, $E_H$, and seismic damage indices of bridge members by Eqs. (5) or (6), presented in the following subsection.

2.2. Seismic damage indices

Under earthquake loading, the damage to and failure of a generic bridge structure are dependent on its deformation, strength and cumulative energy. In order to rationally reflect the elasto-plastic deformation and the effects repeated cycle loading caused by earthquake action, Park et al [23, 24] proposed that classic seismic structural damage can be expressed as a linear combination of the maximum deformation and the hysteretic energy. This may be represented in terms of a damage index [23, 24]:

In which $x_m$ is the maximum deformation under earthquake excitations, $x_u$ is the ultimate deformation under monotonic loading, $F_y$ is the calculated yield strength, $\beta$ is the non-negative parameter or energy dissipation factor.

Direct application of the damage model in Eq. (5) to a bridge structure or member requires the ultimate displacement of the corresponding bridge structure or member to be determined. However, the determination of bridge structure’s ultimate deformation is very difficult for a super high structure or structural member such as reinforced concrete (RC) tower of a long-span CSB. Therefore, Kunnath [25] presented a modified Park’s damage model with the yield moment and curvature replacing the yield force and displacement of Eq. (5). The elastic deformation is not taken into account in Eq. (6). The modified Park’s damage model can be expressed in following form:

In which ${\varphi }_m$ is the maximum curvature of section under earthquake excitations, and ${\varphi }_u$ is the ultimate curvature of section under monotonic loading, ${\varphi }_y$ and $M_y$ is the calculated yield curvature and moment of the section, respectively. For a structural member with the compression and bending, the hysteretic energy, $E_H$, can be obtained by the integral of the hysteretic curve of moment-curvature of structural members in plastic hinge zone.

2.3. Seismic failure criteria

To evaluate structural damage and safety under earthquake, rational seismic damage indices are required. A generic bridge structure, such as the CSB, is composed of different members and materials. Different members, such as RC tower and steel girder, require various seismic damage indices or failure criteria because they behave different mechanical property. Herein, several seismic damage indices and failure criteria are employed to quantitatively assess structural damage and to study the control strategies effects. For RC structures easily experiencing plastic deformation under strong earthquake, Park damage model is widely adopted to describe degree of structural seismic damage. Corresponding damage levels are divided into No Damage (DS1), Minor Damage (DS2), Moderate Damage (DS3), Severe Damage (DS4) and Collapse or Local Failure (DS5); the damage indices are 0-0.1, 0.1-0.25, 0.25-0.40, 0.4-1.0 and ≥1.0, respectively; damage index >1.0 signifies collapse of the structure or local failure of the member [26]. For the steel girder and stay cable, strength-based criteria, including the yield and allowable stress, are employed to evaluate whether they are beyond the elastic range. Yield stress of 460 MPa and allowable stress of 970 MPa are utilized as the critical damage value of the girder and the stay cable, respectively.

3.1. Seismic control strategies

For a passively controlled bridge structure, Eq. (3) indicates that the input energy, $E_I$, can eventually transform into the damping energy, $E_D$, the hysteresis energy, $E_H$, the supplemental damping energy, $E_{dD}$, the supplemental hysteresis energy, $E_{dH}$, the kinetic energy, $E_K$, and the elastic strain energy, $E_S$. The kinetic energy and elastic strain energy diminish near the end of an earthquake. In addition, the structural seismic damage defined by Eqs. (5) or (6) is primarily dependent on the structure’s deformation responses and absorbed hysteretic energy during earthquakes. It is also indicated that a reduction in structural damage can be achieved by decreasing the deformation/curvature responses and hysteresis energy demands, or conversely, by increasing the deformation/curvature and hysteresis energy capacity. Herein, several control strategies may have an effect on reducing the structural seismic damage as follows: (1) improving structural deformation or hysteresis energy capacity; (2) increasing structural damping energy; (3) adding passive energy dissipation device, such as metallic yield damper or viscous fluid damper (VFD); (4) adding nonstructural components used as sacrificial energy dissipation device, such as shear link or buckling restrained brace; (5) by using a combination of these methods.

As mentioned above, the first control strategy, increasing structural deformation/curvature or hysteresis energy capacity, may result in uneconomical structure because of the requirements of the sectional dimensions enhancement and the material increase. The second control strategy, increasing the structural damping energy, is also very difficult because structural damping embodies its own immutable, inherent characteristics. Hence, a viable option is the use of control strategies (3), (4), or (5), resulting in the mitigation of the seismic damage and the improvement of the seismic performance of the structure. Therefore, three passive control systems with the VFDs and a passive hybrid control system incorporating the VFDs and nonstructural components are presented in the following analyses.

3.2. Seismic control targets

For the seismic damage control strategies mentioned above, the damage control objective is as follows: the tower should be controlled to minor damage, which is easily repaired after earthquakes; the corresponding Park damage index is less than 0.25; and the curvature ductility factor is below 3. The pier can be controlled to moderate damage to dissipate more input energy by the plastic deformation, the corresponding Park damage index is less than 0.40 and the curvature ductility factor should not be above 15. Furthermore, the pier suffering severe damage will be within an acceptable range, as long as it is able to carry vertical load. The girder and stay cable should remain elastic, whose stress demands are below their own critical damage values.

4.1. Description of super long-span cable-stayed bridge

A trial designed bridge, as shown in Fig. 1, is a super long-span CSB with a main span of 1400 m [27]. The bridge has an overall length of 2672 m, the span arrangements of which are 150 + 176 + 310 + 1400 + 310 + 176 + 150 m. All RC piers, each with a height of 60 m, consist of four supporting piers (No. 2, No. 3, No. 6 and No. 7 piers) and two side piers (No. 1 and No. 8 piers).

Fig. 1Elevation view of cable-stayed bridge with main span of 1400 m (unit: m)

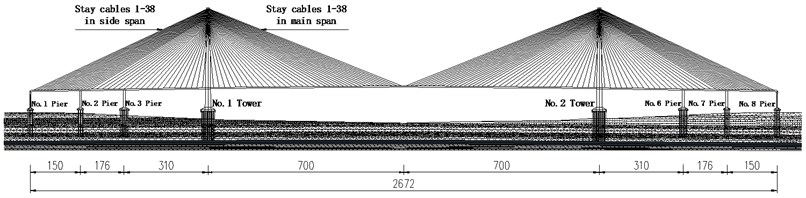
A-shaped RC tower with height of 357 m is shown in Fig. 2, both columns of which are connected by the upper and lower beams to strengthen its transverse stiffness. Baseline cross section of the main girder, 41.0 m wide and 4.5 m high, is an aerodynamically shaped closed box steel girder, as depicted in Fig. 3. There are 304 (38×4×2) stay cables with semi-harp configuration in total, and the longest one is close to 750 m. The pile groups supporting No. 1-No. 3 and No. 6-No. 8 piers, each pile with a diameter of 2.5 m, consist of 19 piles, 19 piles, 36 piles, 36 piles, 19 piles and 19 piles. The length of them are 108 m, 108 m, 98 m, 101 m, 110 m and 108 m, respectively. The pile groups supporting No. 1 and No. 2 towers have 162 piles with a diameter of 2.5 m, and the length of them are 117 m and 114 m, respectively. Due to the scarcity of the geologic structure, the geologic condition of the CSB is same as that of the Sutong bridge, which can rationally reflect the character of the site condition in coastal region.

Fig. 2Elevation view and cross section of tower (unit: m)

Fig. 3Baseline cross section of steel girder (unit: m)

4.2. Finite element modelling

A full 3-D finite element modelling including equivalent nonlinear springs (Fig. 4), considering geometric and material nonlinearities, was conceived to analyze nonlinear seismic response of the CSB in OpenSees [28]. The RC towers and piers were modelled as the fiber elements considering axial force-moment interaction [29]. The main girder was modelled as the elastic beam element. The stay cables were modelled as the truss element with the concept of equivalent elastic modulus, and the connections between the stay cables and tower as well as between the stay cables and girder were modelled as the rigid link. The equivalent nonlinear springs were modelled as the zero-length element, the stiffness and yield strength of which were determined by seismic performance analyses of the pile-soil finite element modelling using push-over analysis, the detailed analyses progress and parameters of the equivalents springs were as referenced in reference [30]. A modified Menegotto and Pinto model [31] including strain hardening was employed for the constitutive modeling of the reinforcing steel bars, and a Mander model [32] considering the effective confinement of stirrups was applied for modeling the concrete. Rayleigh damping was adopted in the 3-D model and the damping ratio was assumed to be 3 % according to the standard code [33].

The connections between the towers and the girder were assumed to be free in the longitudinal direction, as were the connections between the piers and the girder. The displacement restraint was transversely modelled in the 3-D finite element modelling, which was considered to be a constrained system in the following analyses. Furthermore, the effect of the foundation on the seismic response of the CSB was modeled by equivalent nonlinear springs. Hence, the boundary conditions were modelled as translationally and rotationally spring elements in the three orthogonal directions at the bases of the towers and piers, as shown in Fig. 4.

The dynamic characteristics of the CSB were obtained according to the 3-D finite element modelling. The first three modal periods of the CSB in the transverse direction are 14.977, 5.951 and 5.920 s, respectively. In addition, the detailed dynamic characteristics of the CSB were reported in reference [34].

Fig. 43-D finite element modelling of CSB with equivalent nonlinear springs

4.3. Input waves

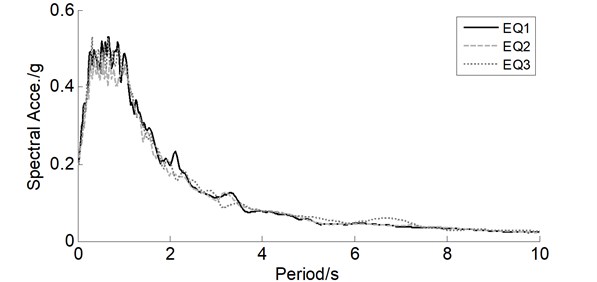
Three artificial waves, previously generated for another long-span bridge, are adopted for the trial designed CSB because of the scarcity of the geologic structure, as plotted in Fig. 5. Each wave includes long period components that have significant influence on this flexible structure, and corresponding acceleration response spectra under 3 % damping are shown in Fig. 6. The peak ground acceleration (PGA) of 0.2 g is representative of the design earthquake wave according to the seismic design guideline [33] and the assumption that the CSB is located in seismic fortification intensity 8.

Fig. 5Acceleration time histories of three artificial waves

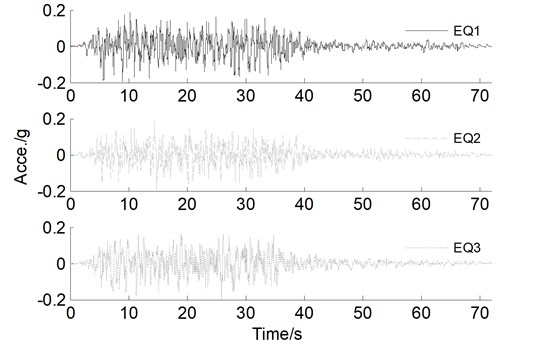
In addition, other earthquake intensities are simulated by amplifying the PGA 2, 4, and 5 times to investigate the seismic damage and failure modes of the CSB in the transverse direction, particularly for a PGA of 1.0 g representing an extreme earthquake. Each input wave is assumed to act uniformly at all supports along the transverse direction of the CSB, and the influence of the longitudinal and vertical earthquake is neglected in this study. Thus, the CSB was subjected to a suite of uniaxial input wave with gradually increasing intensities. In the following analyses, the average demands are obtained and shown for the CSB subjected to three input waves.

Fig. 6Acceleration response spectra of three artificial waves

4.4. Seismic damage and failure modes analyses

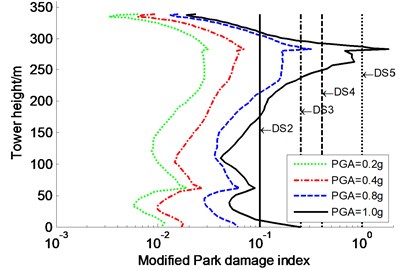
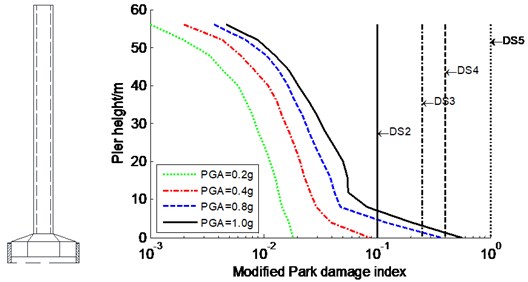
The seismic damage and failure modes of the constrained system designated were studied for the CSB subjected to various seismic intensities of three input waves in the transverse direction. The average modified Park damage indices distribution along the tower and pier are shown in Fig. 7-Fig. 8, respectively. Meanwhile, DS2, DS3, DS4, and DS5 are also plotted in Fig. 7-Fig. 8 to visually assess the seismic damage, which present critical value between both damage stages (similarly hereinafter). However, the results of the partial anchorage region (341-357 m) of the tower is not plotted because this region is within elastic range. Furthermore, a secondary damage index, such as ductility factor, was also introduced to evaluate the seismic damage of super-high RC members. Table 1 only lists the curvature ductility factors at key sections of the tower and piers.

Fig. 7Average modified Park damage indices distribution along tower for constrained system

a)

b)

As shown in Fig. 7-Fig. 8, in the cases of PGA of 0.2 g and 0.4 g, the modified Park damage indices of the tower and piers are less than 0.1, indicating that they are in elastic range and the seismic performance meets seismic design targets based on the standard code [33]. Applying input wave with PGA of 0.8 g has a large impact on the modified Park damage indices of the tower and piers: section 1 of the tower, the No. 2 and No. 3 piers bases experience moderate damage, and the No. 1 pier base suffers from severe damage; corresponding damage indices are 0.314, 0.293, 0.382 and 0.421, respectively. Increasing the PGA to 1.0 g significantly increases the seismic damage along the tower and piers. The vulnerable locations of the tower are still confined to sections 1 and 3 (Fig. 2), which suffer local failure and moderate damage, respectively. Especially of notes, the time difference of both sections getting the maximum damage index is only 1.02 s. The modified Park damage indices at the bases of No. 1, No. 2, and No. 3 piers reach 0.606, 0.452, and 0.564, respectively, which are larger than severe damage value of 0.4. The curvature ductility factors at key sections of the tower and piers increase significantly with the PGA increasing (Table 1). In the case of extreme earthquake (PGA = 1.0 g), sections 1 and 3 (Fig. 2) of the tower and the bases of the piers suffer from severe damage or moderate damage according to curvature ductility factor-based damage criteria (Table 2) determined by the strain criteria. Consequently, it is relatively unsafe to evaluate the seismic damage of the tower and piers by using the curvature ductility factor, rather than by the modified Park damage index. So, only the modified Park damage index is used to assess the effectiveness of control strategies in the following section.

Fig. 8Average modified Park damage indices distribution along pier for constrained system

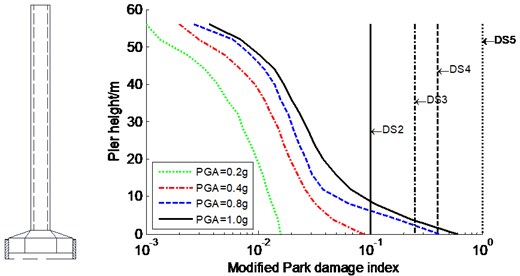
a) No. 1 pier

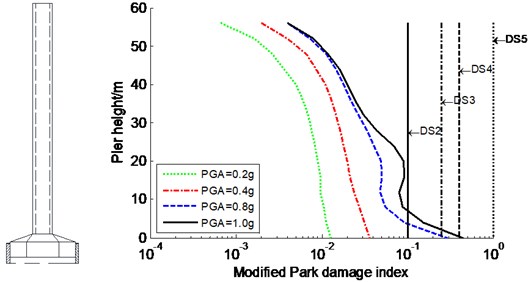
b) No. 2 pier

c) No. 3 pier

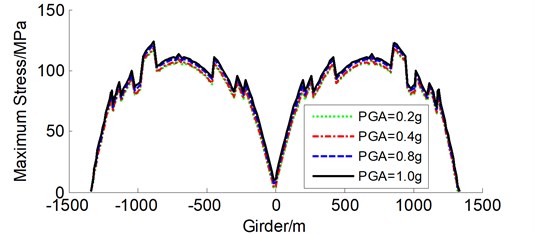
Table 3 and Fig. 9 show the maximum stress demands of typical stay cables 1#, 14#, 25#, and 38# in the side and main spans (see Fig. 1) and the steel girder under various PGAs, respectively. The maximum stress demands of the typical stay cables and steel girder under extreme earthquake are 751.3 MPa and 123.5 MPa, respectively, which are lower than allowable values. This indicates that the stay cables and steel girder are below the elastic limits, which are relatively large redundant. It is concluded that sections 1 and 3 (Fig. 2) of the tower for the constrained system almost simultaneously suffer from local failure and moderate damage, respectively, under extreme earthquake according to Modified Park damage indices, and the tower experiences an unexpected failure mode with double plastic hinges in the transverse direction. This failure mode does not enable the tower to form successively plastic hinge mechanism, which may be different from that of the short- and medium-span CSBs. Therefore, more attention should be paid to the unexpected failure mode when conducting seismic design of long-span CSBs. The piers base also suffers from damage, whereas other regions of the piers remain elastic, indicating that the pier shows a typical flexural failure mode with one plastic hinge. Consequently, the above-mentioned sections are vulnerable to damage under strong earthquake and certain damage control strategy should be suggested in the following section to improve the seismic performance.

Fig. 9Maximum stress envelope curves of girder for constrained system

5.1. Effects of viscous fluid dampers on seismic damage and failure modes

The conventional VFDs are adopted for the control strategies because of its high energy dissipation capacity. Moreover, the effects of VFDs on controlling the members are primarily dependent on the installation locations and parameters of them. Thus, both control strategies, named Strategy A and Strategy B, are presented in this section, the parameters of which are investigated to determine the optimal control effects of the VFDs, as listed in Table 4. In strategy A, the VFDs are only installed between the tower and girder in the transverse direction, damping coefficient $C$ of which is varying from 0 to infinity, as shown in Fig. 10(a). In strategy B, the VFDs are installed between the tower and girder as well as between the pier and girder in the transverse direction, damping coefficient $C$ of which is also varying from 0 to infinity at the pier locations, while damping coefficient $C$ of the VFDs installed at the tower locations is determined through parametric sensivity analyses of strategy A, as depicted in Fig. 10(b). The velocity exponent is assumed to 0.5 for all VFDs that are modelled as the zero-length element, and the mechanical behavior of the material of the VFDs is modelled as the viscous material in OpenSees. The dynamic characteristics of both control strategies are different because of the change of the boundary conditions. As a result, the first mode periods of strategy A and B are 27.465 s and 59.750 s, respectively, in the transverse direction.

Fig. 10VFDs installed at tower and pier locations for strategies A and B (plan view)

a) VFDs installed at tower location for strategy A

b) VFDs installed at tower and pier location for strategy B

The above analyses results indicate that sections 1 and 3 of the tower and the pier bases are easier to suffer from damage and even local failure. Herein, the modified Park damage indices of these sections are only employed to evaluate the effects of the installation locations and damping coefficient $C$ of the VFDs on alleviating the seismic damage of the tower and pier under extreme earthquake (PGA = 1.0 g), as listed in Table 4. The deformation and force demands of the VFDs are listed in Table 5. However, the deformation and force demands of certain VFDs are unavailable in strategies A and B because damping coefficient $C$ is increased to infinity.

As can be seen from Table 4, damping coefficient $C$ of the VFDs in strategy A, varying from 0 to infinity, has a notable effect on the seismic damage at sections 1 and 3 of the tower and at the bases of No. 1, No. 2 and No. 3 piers, whereas it has a minimal influence on the seismic damage at section 2 of the tower. Moreover, the seismic damage indices at section 1 of the tower and at the bases of No. 1 and No. 3 piers firstly decrease and then increase with damping coefficient $C$ of the VFDs increasing, indicating that damping coefficient $C$ of the VFDs exists an optimal value. The maximum deformation demands of the VFDs gradually reduce and the maximum force demands gradually increase as damping coefficient $C$ increased, as listed in Table 5. It can be found that damping coefficient $C$, 16000 kN/(m·s)^0.5, is better than others in strategy A balancing both the seismic damages of the tower and piers and the VFDs demands, corresponding maximum deformation and force demands of the VFD are 1.059 m and 3.955×10⁴ kN, respectively. It was reported that the largest force and stroke requirements of the special dampers for the Messina Strait Bridge were a total load capacity of 8.0×10⁴ kN and a ±2.0 m stroke, respectively [35]. Therefore, the manufactured VFDs are available for this purpose. Compared with the results of the constrained system, the optimal damping coefficient ($C=$ 16000 kN/(m·s)^0.5) in strategy A reduces the maximum damage indices at sections 1 and 3 (Fig. 2) of the tower by 54 % and 67 %, respectively. As a result, section 3 only experiences elastic response, whereas section 1 is subjected to severe damage.

As listed in Table 4, damping coefficient $C$ of the VFDs installed between the pier and girder in strategy B, varying from 0 to infinity, has an obviously adverse effect on section 1 of the tower and has a significant impact on the bases of No. 1, No. 2 and No. 3 piers, while it has a little influence on sections 2 and 3 of the tower. The seismic damage index at section 1 of the tower increases as damping coefficient $C$ increased. The seismic damage indices at the base of No. 1, No. 2 and No. 3 piers firstly decrease and then increase with damping coefficient $C$ increasing, illustrating that damping coefficient $C$ of the VFDs exists an optimal value. In addition, the maximum deformation demands of the VFDs monotonically reduce, in reverse, the maximum force demands increase, as listed in Table 5. It is revealed that damping coefficient $C=$ 2000 kN/(m·s)^0.5 of the VFDs installed at the pier locations is better than others in strategy B balancing both the seismic damages of the tower and piers and the VFDs demands. Compared to the results of the constrained system, the optimal damping coefficient ($C=$ 2000 kN/(m·s)^0.5) in strategy B reduces the seismic damage index at section 1 of the tower by up to 60 %, however, the section is still subject to severe damage. Thus, the control strategies cannot entirely control the seismic damage of the tower, and the tower does not meet damage control targets and need to be further studied by other control strategies. The possible reasons are that: (1) the partial inertia force of the girder transferred to the tower by the cables increases slightly because of the connections between the tower and girder changing; (2) the upper beam may lead to the stress concentration at section 1 of the tower. The optimal damping coefficient ($C=$ 2000 kN/(m·s)^0.5) in strategy B reduces the maximum damage indices at the bases of No. 1, No. 2, and No. 3 piers by up to 65 %, 54 %, and 62 %, respectively, comparison to the results of the constrained system. Consequently, the controlled piers suffer moderate damage which satisfy seismic control targets.

5.2. Influences of connection modes of upper beam on seismic damage and failure modes

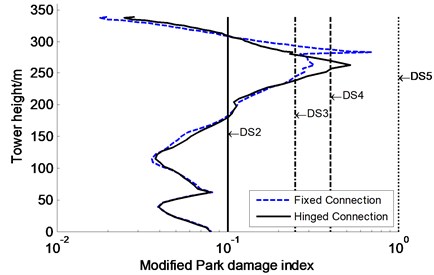
From the above analyses, the tower still suffers from severe damage even if the optimal VFDs were installed at the tower and pier locations, which did not satisfy seismic control targets. One of possible causes is the connection stiffness between the upper beam and tower leading to stress concentration of the tower. Herein, only the connection stiffness between both members decreases to zero on the basis of strategy B with the optimal VFDs, namely the connection modes between both members change from fixed connection to hinged connection, as depicted in Fig. 11. The nonlinear time history analyses are performed to evaluate the influence of the connection between both members on the seismic damage of the tower under extreme earthquake (PGA = 1.0 g). The modified Park damage indices distribution along the tower is shown in Fig. 12, where “Fixed connection” and “Hinged connection” represent the fixed and hinged connections between the upper beam and tower on the basis of strategy B with the optimal VFDs, respectively. Whereas the seismic damage and demands of other members, such as piers and VFDs, are not plotted and discussed because the change of the connection stiffness between both members has few influence on the seismic response of them.

Compared with the results of “Fixed connection”, “Hinged connection” reduces the modified Park damage index at section 1 of the tower by 64 %, while has little influence on the seismic damage at sections 2 and 3 of the tower. The modified Park damage indices are 0.240, 0.079, and 0.080, respectively, which are less than the moderate damage value of 0.25 or even the minor damage value of 0.1, indicating that the sections meet seismic control targets based on seismic damage criteria. However, it is noted that several new sections nearby section 1 are subjected to unexpected severe damage, such as the modified Park damage indices of the sections at tower height 257 m, 263 m, and 269 m are 0.407, 0.525, and 0.40, respectively, which do not satisfy seismic control targets. Anyway, “Hinged connection” can effectively mitigate the seismic damage distribution along the tower to a certain degree, for instance, the maximum modified Park damage index of the section at tower height 263 m for “Hinged connection” is 75 % that of section 1 of the tower for “Fixed connection”. It is clearly concluded that the seismic damage of the tower does not meet seismic control target when adopting the hinged connection between the upper beam and tower. Thus, the tower will be further investigated to meet seismic control targets and improve its failure modes by using other control strategies in following subsection.

Fig. 11Both connection modes between upper beam and tower

a)

b)

Fig. 12Influence of connection modes between upper beam and tower on modified Park damage indices distribution along tower

a)

b)

5.3. Effects of inelastic links on seismic damage and failure modes

Additional inelastic links are applied to A-shape tower of the CSB on the basis of strategy B with the optimal VFDs located between the tower and girder as well as the pier and girder, the effects of which on the seismic damage of the tower are primarily dependent on the main parameters of them. Therefore, the optimal parameters of the inelastic links, including the flexural stiffness, yielding moment, and installation locations and amounts, are obtained from parametric sensitivity analyses, which are used to design the inelastic links made of low-yield steel, as shown in Fig. 13. And local buckling of the inelastic links is also verified according to the guidelines [36]. However, the detailed results are not presented in this paper. Then nonlinear time history analyses are performed to study the influence of the inelastic links on the seismic damage and failure modes of the tower for the CSB subjected to extreme earthquake (PGA = 1.0 g). The modified Park damage indices distribution along the tower is shown in Fig. 14, in which “combination strategy” represents the control strategy combining the inelastic links and the optimal VFDs in strategy B. In addition, the maximum moment, transverse shear force and transverse displacement of the tower are also shown in Fig. 15. Whereas the seismic damage and demands of other members, such as piers and VFDs, are not shown and discussed because the inelastic links have few influence on their seismic response. The results of strategy B with the optimal VFDs (named “Fixed Connection” in Section 5.2) and the constrained system are plotted in Fig. 14 and Fig. 15 for comparison.

Fig. 13Inelastic links installed on tower

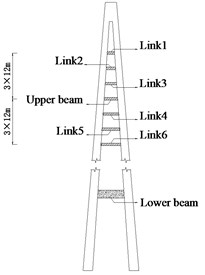
a) Inelastic links installed for tower

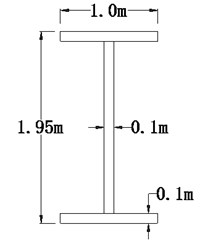
b) Cross section of inelastic link

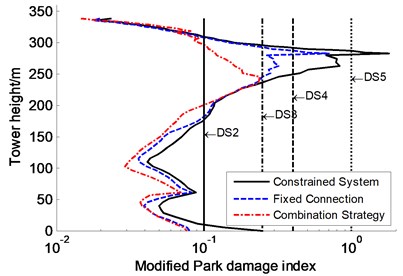
Fig. 14Effects of inelastic links on controlling modified Park damage indices distribution along tower

a)

b)

Fig. 15Influences of inelastic links on seismic response along tower

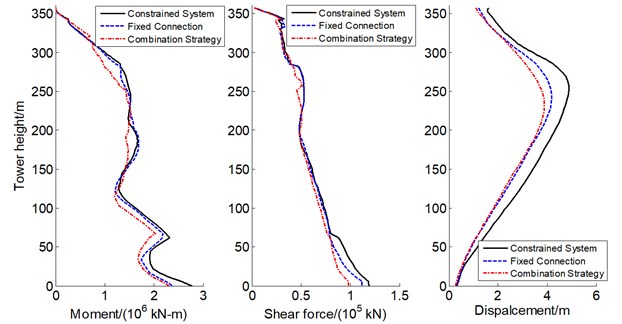
It can be seen in Fig. 14 that the combination strategy enables the tower to only experience minor damage and even no damage, such as the maximum modified Park damage index is only 0.238 at tower height 245 m, and 0.12 at section 1 of the tower, which are less than moderate damage value of 0.25. Furthermore, the combination strategy can effectively decrease the moment, transverse shear force and transverse displacement of the tower, such as the maximum moment and shear force at tower base reduce approximately 20 % comparison with the results of the constrained system, and the maximum displacement at tower height 251 m decreases 23 %, as shown in Fig. 15. It is concluded that the combination strategy can effectively control the seismic damage and improve the failure modes of the tower so as to increase the collapse resistant capacity of the CSB, which enable the CSB to satisfy the seismic control target according to seismic damage criteria.