Abstract
In this paper, a preventive maintenance optimization policy based on a three-stage failure process in finite time horizon is proposed. The lifetime of system is divided into three stages by the concept of three-stage failure process, which is corresponding to the three color scheme commonly used in industry. The subsequent inspection interval is halved when the minor defective stage is identified. Once identifying the severe defective stage, maintenance action is carried out. A numerical example is presented to demonstrate the efficiency of the proposed models.
1. Introduction
Most industrial equipment systems will suffer from stochastic failure due to degradation, operational and environmental conditions, which may interrupt the production process and result in serious losses. Therefore the action that taking effective methods to reduce the impact of stochastic failure is important.
Maintenance activities consist of corrective and preventive maintenance taken in order to minimize the serious consequences of unexpected failures. Preventive maintenance (PM) policy is the feasible approaches to be taken to reduce the impact of equipment failure. The current work belongs to the inspection PM policy is an important problem.
A common assumption of inspection modeling is that the system will be used over an effectively infinite time horizon. There have been not many papers that treated maintenances for a finite time horizon, because it is more difficult theoretically to discuss optimal policies for a finite time horizon. However, the time horizon of use period is always finite in practice. Therefore, maintenance plans have to be reestablished at appropriated times for a specified finite interval.
A summary of maintenance policies for a finite interval is developed, which including replacement policies (periodic replacement with minimal repair, block replacement and simple replacement), imperfect preventive maintenance policies and inspection policies [1]. The paper presents an accurate approximation to find an approximate optimal solution of the sequential age replacement policy for a finite-time horizon [2]. Periodic and sequential preventive maintenance policies over a finite planning horizon with a dynamic failure law are proposed [3].
This paper proposed a preventive maintenance policy for finite time horizon based on a three-stage failure process. As we all knows, the two-stage delay time concept, has obvious advantage for optimizing the inspection intervals. However, the state of system may by described more than two before failure as three color scheme is mostly used to divide the state before failure into green (normal), yellow (need attention), and red (need immediate attention) in industrial applications. Therefore, Wang firstly extended the two-stage delay time to a three-stage failure process, where the traditional failure delay time stage is further divided into two stages: minor defective stage and severe defective stage [4, 5]. Yang developed imperfect inspection maintenance models based on a three-stage failure process [6, 7]. All of the current models based on the three-stage failure process mostly consider the infinite time horizon, but the time horizon of use period is mostly finite in reality. Therefore, this paper focuses on the three-stage failure process inspection modeling for finite time horizon.
The remaining parts of the paper are organized as follows: Section 2 presents the problem description and modeling assumptions. The preventive maintenance policy based on the three-stage failure process for finite time horizon is formulated in Section 3. Section 4 gives numerical examples and some discussions. Finally, Section 5 concludes the paper.
2. Modeling assumptions and notation
The following modeling assumptions and notation are presented for model building.
1) A single component system is considered, which only subject to a single dominant failure mode.
2) The failure process of system is divided into three stages: normal stage , minor defective stage and severe defective stage . These three stages are assumed to be independent.
3) The time horizon considered is finite with (0, ], which is common in practice.
4) The system is inspected with an equal interval . The total length is a multiple of inspection interval as for simplicity.
5) Inspections are assumed to be perfect, which means the minor and severe defective stages can be detected immediately.
6) When the minor defective stage is identified, the subsequent inspection interval is halved. And once identifying the severe defective stage, the system is repaired immediately. Failure can be found and replacement is implemented for avoiding the huge economical loss and severe consequence.
The subsequent modeling will use the following notation:
, , random variable representing the duration of normal stage, probability density function (pdf) and cumulative distribution function (pdf) of normal stage;
, , random variable representing the duration of minor defective stage, pdf and cdf of minor defective stage;
, , random variable representing the duration of severe defective stage, pdf and cdf of severe defective stage;
inspection interval;
random failure time;
random time of an inspection renewal for identifying the severe defective stage;
average downtime per inspection;
average downtime per failure;
average downtime caused by an inspection renewal for identifying the severe defective stage;
average availability.
3. Preventive maintenance policy based on a three-stage failure process
The preventive maintenance policy based on a three-stage failure process is proposed in this section to optimize the inspection interval for finite time horizon. The objective function is to maximize the average availability. In the finite time horizon (0, ], the average availability includes three mutually exclusive events.
3.1. Failure renewal
Failure renewal means the system fails within an inspection interval before identifying the severe defective stage or reaching the finite use limit . Two different failure renewal scenarios are considered according to the case whether the minor defective stage is identified.
3.1.1. No minor defective stage is identified
The system fails in before any defective stages are identified. As shown in Fig. 1, The minor and severe defective stages happen within the same interval . The probability of such a failure renewal is:
Fig. 1The system fails in i-1T,iT before identifying any defective stages
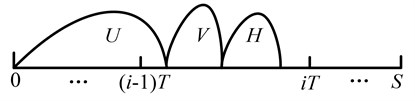
3.1.2. Identifying the minor defective stage by an inspection
The system fails in after identifying the minor defective stage by an inspection. The system deteriorates into minor defective stage within . However, the minor defective stage is identified at and the subsequent inspection interval is halved, as depicted in Fig. 2. The probability of such a renewal is:
Therefore, the downtime of failure renewal can be derived from Eqs. (1) and (2).
Fig. 2The system fails in iT+m-1T2,iT+mT2 after identifying the minor defective stage at iT

3.2. Inspection renewal
Inspection renewal occurs once the severe defective stage is identified before reaching the finite use limit or failing. Similarly, there are also two different inspection renewals depending on whether the minor defective stage is identified.
3.2.1. No minor defective stage is identified
Fig. 3 shows the scenario that the system is renewed when the severe defective stage is found at before any minor defective stage is identified. So the probability of such an inspection renewal is:
Fig. 3The system renews at iT before any minor defective stage is identified
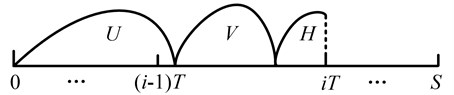
3.2.2. Identifying the minor defective stage by an inspection
Fig. 4 presents the scenario that inspection renewal occurs at when the minor and severe defective stages are identified at and respectively. The probability of such a renewal is:
Therefore, the downtime of inspection renewal can be derived from Eqs. (4) and (5).
Fig. 4The system renews at iT+mT2 after the minor defective stage is identified at iT

3.3. No renewal
The system does not happen any renewals but reach the finite use limit . Although any renewals are not emerged, there also exist two scenarios.
3.3.1. No minor defective stage is identified
The system reaches the finite use limit S before any defective stages are identified, as shown in Fig. 5. However, there may exist three possible scenarios according to the length of three stages. The probability of such an event is:
Fig. 5The system reaches finite use limit S before any defective stages are identified
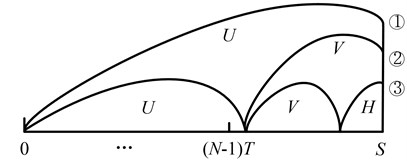
3.3.2. Identifying the minor defective stage by an inspection
The system reaches finite use limit after the minor defective stage is found at . There also exist two different scenarios, see Fig. 6. The probability of such an event is:
The downtime of no renewal can be derived from Eqs. (7) and (8) as:
Fig. 6The system reaches finite use limit S after identifying the minor defective stage at mT
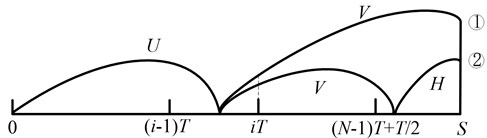
3.4. Objective function
4. Numerical example
A numerical example is presented in this section to demonstrate the efficiency of the proposed models and derive the optimal inspection intervals. These three stages are assumed to follow Weibull distributions and the pdf of the th (1, 2 and 3) stage is:
where , are scale parameter and shape parameter respectively.
Table 1Distribution parameters
0.01 | 3 | 0.02 | 2 | 0.04 | 1 |
Table 2Downtime parameters
1 | 3 | 20 | 0.6 |
The distribution parameters for these stages and downtime parameters are assumed in Tables 1 and 2 respectively. In this example, the finite time limit is 300. According to the proposed models, the optimal inspection intervals are derived under different values of , as shown in Table 3. The optimal 9, 33.3, and the optimal availability 0.9559. Of course, the result is largely depending on the relevant parameters. The proposed models can help managers to make scientific maintenance decisions for such system with finite time horizon.
Table 3The results of proposed models
3 | 100 | 0.9474 | 11 | 27.3 | 0.9550 |
4 | 75 | 0.9507 | 12 | 25 | 0.9543 |
5 | 60 | 0.9530 | 13 | 23.1 | 0.9534 |
6 | 50 | 0.9545 | 14 | 21.4 | 0.9523 |
7 | 42.9 | 0.9554 | 15 | 20 | 0.9512 |
8 | 37.5 | 0.9558 | 16 | 18.75 | 0.9499 |
9 | 33.3 | 0.9559 | 17 | 17.65 | 0.9486 |
10 | 30 | 0.9556 | 18 | 16.67 | 0.9472 |
5. Conclusions
As finite time horizon of equipment use period is common in practice, a preventive maintenance optimization policy based on a three-stage failure process in finite time horizon is proposed in this paper aiming at optimizing the inspection intervals. Three states of system are divided before failure by the concept of three-stage failure process, namely normal, minor defective and severe defective. A numerical example is presented to demonstrate the efficiency of the proposed models. The results show that according to the proposed models and given parameters, the optimal inspection interval can be derived, which can be helpful for maintenance managers to make scientific maintenance decisions.
References
-
Nakagawa T., Mizutani S. A summary of maintenance policies for a finite interval. Reliability Engineering and System Safety, Vol. 94, 2009, p. 89-96.
-
Jiang R. An accurate approximate solution of optimal sequential age replacement policy for a finite-time horizon. Reliability Engineering and System Safety, Vol. 94, 2009, p. 1245-1250.
-
Schutz J.,·Rezg N., Léger J. B. Periodic and sequential preventive maintenance policies over a finite planning horizon with a dynamic failure law. Journal of Intelligent Manufacturing, Vol. 22, 2011, p. 523-532.
-
Wang W. An inspection model based on a three-stage failure process. Reliability Engineering and System Safety, Vol. 96, 2011, p. 838-848.
-
Wang W., Zhao F., Peng R. A preventive maintenance model with a two-level inspection policy based on a three-stage failure process. Reliability Engineering and System Safety, Vol. 121, 2014, p. 207-220.
-
Yang R. F., Yan Z. W., Kang J. S. An inspection maintenance model based on a three-stage failure process with imperfect maintenance via Monte Carlo simulation. International Journal of Systems Assurance Engineering and Management, Vol. 6, Issue 3, 2015, p. 231-237.
-
Yang R. F., Zhao F., Kang J. S., Li H. P., Teng H. Z. Inspection optimization model with imperfect maintenance based on a three-stage failure process. Eksploatacja i Niezawodnosc – Maintenance and Reliability, Vol. 17, Issue 2, 2015, p. 165-173.
