Root mean square error criterion using operational deflection shape curvature for structural damage detection

Bakhshizade, Ali; Ashory, Mohammad Reza

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 30 December 2015

Check for updates

Root mean square error criterion using operational deflection shape curvature for structural damage detection

Ali Bakhshizade¹

Mohammad Reza Ashory²

¹Department of Mechanical Engineering, Roshdedanesh Institute of Higher Education, Semnan, Iran

²Modal Analysis Lab, School of Mechanical Engineering, Semnan University, Semnan, Iran

Corresponding Author:

Ali Bakhshizade

Cite the article Download PDF

Downloads 1208

Abstract

Detection of structural damages using the vibration test data has been investigated by many researchers in the last decades. Identification of the defect in the early stages can prevent the unpredicted failure of structure. For beam-like structures, curvature techniques, e.g., mode shape curvature and flexibility curvature have been applied to localize the damage. In this paper, root mean square error using operational deflection shape curvature is used for damage detection. Differential Quadrature Method (DQM) is implemented to obtain the curvatures of the operational deflection shape. To demonstrate the effectiveness of method, the finite element model of a cantilever beam is used. The model is excited and the responses are measured in the simulated test. Enhanced frequency domain decomposition (EFDD) is used to extract the modal parameters. Also Mass change method is used to scale the mode shapes through which the scaled ODS parameters are computed. Using the RMSE the location of the damage is identified. The results show that this approach is more effective than the previous methods

1. Introduction

Damage in the structural and mechanical systems is defined as changes in the material and/or geometric properties of these systems, including changes in the boundary conditions and system connectivity, which adversely affect the current or future performance of these systems” [1]. Vibration based techniques have been widely expanded in few decades. These methods localize the flaws and defects in structures based on changes in the modal parameters (natural frequencies, mode shapes and damping ratio).

These methods can be classified in many ways but the damage classification system presented by Rytter [2] is adopted here, which defines four levels of damage assessment:

1) (detection): determination that whether the damage is present in the structure;

2) (localization): determination of the geometric location of the damage;

3) (quantification): determination of the severity of damage;

4) (prediction): prediction of the remaining service life of the structure.

The aim of investigations in the last 20 years has been the global and on-line nondestructive evaluation. Amongst the techniques under development one can outline those using mechanical vibrations, smart materials, image processing, optical fibers, novelty based and statistical information. Vibration-based methods have been applied successfully on large and complicated structures such as civil engineering structures (mostly bridges), aerospace structures and composite structures. During the last decades, research on vibration-based structural damage identification methods has been expanding rapidly.

Some of the existing methods in vibration are based on the comparison between the parameters extracted from experimental observations and numerical models of the structure; there are also methods based on the comparison between parameters identified from experimental-only observations [3].

The method presented in this paper is in the category of methods that use the change in the operational deflection shapes (ODSs) to detect, locate and relatively quantify the damage.

2. Theory

2.1. Frequency domain decomposition (FDD) method

The Frequency Domain Decomposition (FDD) method is proposed by Brincker et al. [4, 5]. In this method first the Power Spectral Density (PSD) of the response is computed. Then the singular value decomposition is applied to obtain the modal parameters of system. The relation between the inputs and outputs is given by [5]:

1

G_{y y} (j ω) = \bar{H} (j ω) G_{x x} (j ω) H^{T} (j ω),

where $G_{x x}$ is the PSD matrix of input, $G_{y y}$ is the PSD matrix of output and $H (j ω)$ is the FRF matrix. If the input force is assumed to be a white signal, the PSD of the output can be given by:

2

G_{y y} (j ω) = \sum_{K = 1}^{n} \frac{d_{k} ϕ_{k} ϕ_{k}^{t}}{j ω - λ_{k}} + \frac{{\bar{d}}_{k} {\bar{ϕ}}_{k} {\bar{ϕ}}_{k}^{t}}{j ω - {\bar{λ}}_{k}},

where $d_{k}$ is a scalar, $ϕ_{k}$ is the $k$ th mode shape vector, $γ_{k}$ is the modal participation vector, $λ_{k}$ is the $k$ th complex resonance frequency, $(\bar{∙})$ sign stands for the complex conjugate and $t$ indicates the transpose of a matrix.

The PSD of response in each frequency can be decomposed to the singular values and singular vectors using the following equation:

3

{\hat{G}}_{y y} (j ω_{i}) = U_{i} S_{i} U_{i}^{H},

where $U_{i}$ is the $i$ th singular vector, $S_{i}$ is the $i$ th singular value, $ω_{i}$ is the $i$ th frequency and $H$ indicates the complex conjugate of a matrix.

The peaks of first singular values of system correspond to the natural frequencies of system. The singular vectors corresponding to the peaks of first singular values approximate the mode shapes.

2.2. Mass change method

In output only modal analysis, the mode shapes are not scaled. Mass change method is a method for scaling of mode shapes.

For a natural frequency $ω_{n 1}^{}$ , and the corresponding mode shape $\{ϕ_{1}\}$ of a MDOF system, if the masses of vibrating system at some or all of the degrees of freedom are changed, the $r$ th natural frequency and the corresponding mode shapes are changed to $ω_{n 2}^{}$ and $\{ϕ_{2}\}$ respectively. Considering small changes of mass matrix, it can be assumed that the mode shapes change negligibly [6]. Therefore:

4

\{ϕ_{2}\} ≅ \{ϕ_{1}\} = \{ϕ\} .

The relation between the unscaled mode shape $\{ψ\}$ and the scaled mode shape $\{φ\}$ is:

5

\{ϕ\} = α \{ψ\},

where $α$ is the scaling factor.

It is shown in [6], that the best scaling factor is obtained when the mode shapes are scaled to the length and both the modified and unmodified mode shapes are used:

6

α_{12} = \sqrt{\frac{(ω_{n 1}^{2} - ω_{n 2}^{2})}{ω_{n 2}^{2} {\{ψ_{1}\}}^{T} \cdot [Δ M] \cdot \{ψ_{2}\}}},

where $[Δ M]$ is the mass change matrix, $\{ψ_{1}\}$ and $\{ψ_{2}\}$ are the unscaled mode shapes before and after mass change.

2.3. ODS estimation

Frequency response function can be obtained using the following equation [7]:

7

α_{j k} (ω) = \sum_{r = 1}^{N} \frac{(φ_{j r}) (φ_{k r})}{ω_{r}^{2} - ω^{2} + i η_{r} ω_{r}^{2}},

where $η$ is the damping ratio and $α$ the receptance matrix. Damping ratio can be obtained from EFDD method. The column vector, k, of the receptance matrix, $\{α_{k (ω)}\}$ , is the ODS at frequency $ω$ . Therefore, the ODS describes the shape exhibited by the structure at each excitation frequency $ω$ , given by the responses and normalized by the applied forces.

3. Damage detection

3.1. Theory

When a structure is damaged its stiffness and damping alter and, as a result does the receptance matrix:

8

[α^{d} (ω)] = {([K^{d}] + i ω [C^{d}] - ω^{2} [M])}^{- 1},

where the superscript $d$ stands for “damaged”. It is reasonable to assume that the smaller the degree of correlation between the column vectors (ODSs), $\{α j (ω)\}$ and $\{d α j (ω)\}$ , the larger the damage. Root mean square error using the spectral strain energy was first studied by Bayissa and Haritos [8]. In this paper is used the curvature of ODS instead of spectral strain energy in root mean square error criterion:

9

R M S E (ω) = \sqrt[]{\frac{\frac{1}{N} \sum_{i = 1}^{N} {(α_{i}^{d^{''}} (ω) - α_{i}^{''} (ω))}^{2}}{\frac{1}{N} \sum_{i = 1}^{N} {(α_{i}^{''} (ω))}^{2}}},

where $N$ is the number of measurement points. But central difference can not present the curvature accurately, two nodes are missing in the approximation and it needs to many points of measurement. In this work, differential quadrature method was used to obtain the curvature.

3.2. Differential quadrature method (DQM)

The idea of using differential quadrature method is to quickly compute the derivative of a function at any grid point within its bounded domain by estimating a weighted linear sum of values of function at a small set of points related to domain. According to this method nth derivative of $f (x)$ can be approximately obtained by:

10

{\frac{\partial^{n} f (x)}{{\partial x}^{n}}|}_{x = x_{i}} = \sum_{j = 1}^{N_{x}} A_{i j}^{x (r)} f (x_{j}), i = 1, 2, \dots, N_{x}, r = 1, 2, \dots, N_{x} - 1 .

In order to determine the weighting coefficients a specific test function is required. One of the best approaches has been proposed by Quan and Chang [9, 10]. They used the Lagrange interpolation function as test function and determined the weighting coefficients on this basis. Weighting coefficients for the first-order derivatives are:

11

A_{i j}^{x (1)} = \{\begin{array}{l} \frac{P (x_{i})}{(x_{i} - x_{j}) P (x_{j})}, i \neq j, \\ - \sum_{\begin{matrix} j = 1 \\ i \neq j \end{matrix}}^{N_{x}} A_{i j}^{x (1)}, i = j, i, j = 1, 2, \dots, N_{x} . \end{array}

12

P (x_{i}) = \prod_{j = 1, i \neq j}^{N_{x}} (x_{i} - x_{j}) .

To evaluate the weighting coefficients of higher order derivatives recurrence formulae are derived as:

13

A_{i j}^{x (r)} = r [A_{i i}^{x (r - 1)} A_{i j}^{x (1)} - \frac{A_{i j}^{x (r - 1)}}{x_{i} - x_{j}}], i, j = 1, 2, \dots, N_{x}, i \neq j, 2 \leq r \leq N_{x} - 1,

14

A_{i i}^{x (r)} = - \sum_{j = 1, i \neq j}^{N_{x}} A_{i j}^{x (r)}, i = 1, 2, \dots, N_{x}, 1 \leq r \leq N_{x} - 1 .

4. Numerical case study

A study based on finite element model of a cantilever beam was conducted to evaluate the feasibility of applying curvature of ODS in RMSE criterion to identify the crack of a beam-structure. The geometry of the beam and its material properties are as follows: Young’s modulus $E =$ 206 GPa, density $ρ =$ 7800 kg/m³, length $l =$ 800 mm, Cross sectional area $A = w \times h =$ 32 mm × 16 mm. The total number of elements is 8 and two damage cases are studied. Damage characteristics have been described in Table 1.

Table 1Damage scenarios

	$l_{1}$ (mm)	Element number	$a$ (mm)
Case I	650	6	0.8
Case II	450	3	0.6

Fig. 1Geometry of cantilever beam with a crack

Damage is simulated with a method that is proposed by Nahvi and Jabbari [11]. In this method the length of damaged element is smaller than the other elements.

The application of ODS curvature using DQM compared to the method presented in [8] for the above cases have been shown in the Figs. 2-5.

Fig. 2Method in [8] (Case I)

Fig. 3Proposed method (Case I)

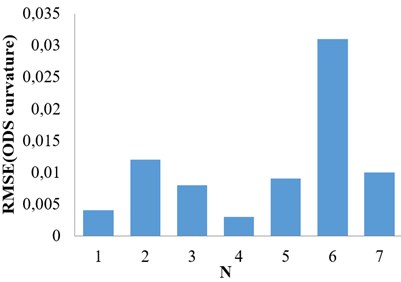
Fig. 4Method in [8] (Case II)

Fig. 5Proposed method (Case II)

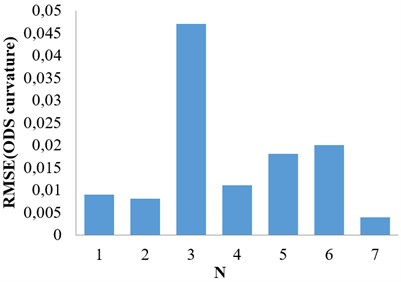
For case (I), the proposed method shows that the damage is between nodes 6 and 7 (Fig. 3). The result is concluded from Fig. 2. However, the difference in Fig. 3 is more indicative compared to the result in Fig. 2. The same conclusion can be found for case II by comparing Figs. 4 and 5.

5. Conclusion

In this study, a new method is developed to improve the damage localization of a beam structure which has been numerically investigated. Results show that the proposed approach can be used to localize the damage in the structure without any analytical model. When the number of measurement points is limited, DQM method has the good accuracy and the less time of computation. In comparison with method in [8] that need, a large number of measurement points to obtain an accurate result, the proposed method has inherent advantages of finding cracks where the method suggested in [8] is relatively weak.

References

Sohn H., Farrar C. R., Hemez F. M., Shunk D. D., Stinemates S. W., Nadler B. R., Czarnecki J. J. A Review of Structural Health Monitoring Literature Form 1996-2001. Los Alamos National Laboratory Report LA-13976-MS, 2004.

Search CrossRef
Rytter A. Vibration Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Department of Building Technology and Structural Engineering, Aalborg University, 1993.

Search CrossRef
Farrar C. R., Doebling S. W. The state of the art in vibration-based structural damage identification. 2-day Short Course, Madrid, Spain, 2000

Search CrossRef
Brincker R., Zhang L., Andersen P. Modal identification from ambient responses using frequency domain decomposition. Proceedings of 18th International Modal Analysis Conference, Florida, 2000.

Search CrossRef
Brincker R., Zhang L., Andersen P. Modal identification of output only systems using frequency domain decomposition. Journal of Smart Materials and Structures, Vol. 10, 2001, p. 441-445.

Search CrossRef
Aenlle M. L., Brincker R., Canteli A. F. Some methods to determine scaled mode shapes in natural input modal analysis. Proceedings of 23rd International Modal Analysis Conference, Florida, 2005.

Search CrossRef
Maia N. M. M. Theoretical and Experimental Modal Analysis. Research Studies Press Ltd, 1997

Search CrossRef
Bayissa W. L., Haritos N. Structural damage identification in plates using spectral strain energy analysis. Journal of Sound and Vibration, Vol. 307, 2007, p. 226-249.

Search CrossRef
Quan J. R., Chang C. T. New insights in solving distributed system equations by the quadrature methods – Part 1. Computers and Chemical Engineering, Vol. 13, 1989, p. 779-788.

Search CrossRef
Quan J. R., Chang C. T. New insights in solving distributed system equations by the quadrature methods – Part 2. Computers and Chemical Engineering, Vol. 13, 1989, p. 1017-1024.

Search CrossRef
Nahvi H., Jabbari M. Crack detection in beams using experimental modal data and finite element model. International Journal of Mechanical Science, Vol. 47, 2005, p. 1477-1497.

Search CrossRef

About this article

Received

17 September 2015

Accepted

18 October 2015

Published

30 December 2015

Keywords

operational deflection shape

differential quadrature

RMSE

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.